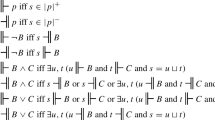Abstract
Adding a transparent truth predicate to a language completely governed by classical logic is not possible. The trouble, as is well-known, comes from paradoxes such as the Liar and Curry. Recently, Cobreros, Egré, Ripley and van Rooij have put forward an approach based on a non-transitive notion of consequence which is suitable to deal with semantic paradoxes while having a transparent truth predicate together with classical logic. Nevertheless, there are some interesting issues concerning the set of metainferences validated by this logic. In this paper, we show that this logic, once it is adequately understood, is weaker than classical logic. Moreover, the logic is in a way similar to the paraconsistent logic LP.
Similar content being viewed by others
Notes
It will be useful to assume that \(\mathcal {L}\) contains a falsity constant ⊥ and a truth constant ⊤, in addition to the usual connectives and quantifiers.
To simplify things, our language lacks an identity predicate. Notice that because of the way in which we handle self-reference (denotations are fixed through the models), identity is not really needed for that purpose. In any case, as Ripley himself points out, a different approach could be used -such as employing Peano arithmetic as our naming system or having a quote-name forming device in the language. The results we reach below do not depend in any way on this issue, although the proofs might have been slightly different.
We will work in a multiple conclusions setting. Nothing important hangs on this, but the approach we are going to consider below makes use of multiple conclusions, so working with them from the start will simplify the discussion.
We use the notation \(\textit {L}^{+}\) to stress that the logic L already contains a transparent truth predicate, that is, a predicate T(x) such that for any formula A and any valuation v, v(T〈A〉)=v(A).
There are also additional problems with these theories. For instance, the weakness of the conditional produces complications with restricted quantifications (see [4]). Also, these theories cannot include a naive notion of validity because of the Validity Paradox (see [5]). However, we will not address these issues here.
In the proof we use Greek letters to represent meta-schematic variables. We need meta-schematic letters because the proof is about schematic formulas. For example, ϕ may represent A∨B; and A∨B may represent (p∧q)∨(r∧s) under some replacement function.
To keep things as simple as possible, in this section we will not use multiple conclusions, and we will assume that the sets Δ i are always finite. Nothing important hangs on this though.
Notice that we need to quantify over uniform replacements in both sentences. If the quantifiers were to range over the entire equivalence, the statement would be false. In other words, it is false that: (For every uniform replacement σ of δ∈Δ i and ψ i by formulas of the language), the following sentences are equivalent: (a) if \(\sigma ({\Delta }_{1}) \vDash _{ST^{+}} \sigma (\psi _{1})\) and ... and \(\sigma ({\Delta }_{n}) \vDash _{ST^{+}} \sigma (\psi _{n})\) , then \(\sigma ({\Delta }) \vDash _{ST^{+}} \sigma (\psi )\) . (b) \(\sigma (t({\Delta }_{1} \vDash \psi _{1}))\) , ..., \(\sigma (t({\Delta }_{n} \vDash \psi _{n})) \vDash _{LP^{+}} \sigma (t({\Delta } \vDash \psi ))\) . Just as a counterexample, take (a) \(A, A \supset B \vDash _{LP^{+}} B\) , and (b) if \(\vDash _{ST^{+}} A\) and \(A \vDash _{ST^{+}} B\) , then \(\vDash _{ST^{+}} B\) . Now replace A by p and B by q. So the first claim, ‘ \(p, p \supset q \vDash _{LP^{+}} q\) ’, would be false, while the second claim, ‘if \( \vDash _{ST^{+}} p\) and \(p \vDash _{ST^{+}} q\) , then \( \vDash _{ST^{+}} q\) ’, would be true, because its antecedent is false (p is not a tautology in ST + ).
An anonymous referee has suggested the following counterexample: (a) It is true that (for every replacement): if \(A \vDash _{ST^{+}} B \wedge \neg B\) , then \(A \vDash _{ST^{+}} C\) . (b) But it is false that (for every replacement): \(A \supset (B \wedge \neg B) \vDash _{LP^{+}} A \supset C\) . However, this is not a counterexample to our theorem. Because while observation (b) is correct, observation (a) is incorrect. In particular, \(p \vDash _{ST^{+}} \lambda \wedge \neg \lambda \) , but \(p \nvDash _{ST^{+}} q\).
As an anonymous referee pointed out to us, a similar result applies to \(K_{3}^{+}\). In particular, the First Collapse Result would still hold after replacing L P + by \(K_{3}^{+}\) and S T + by T S + (where T S + is the tolerant-to-strict consequence relation, dual to S T +).
In the literature it is common to find an alternative reading of three-sided sequents in terms of negative conjunctions. On that reading, Γ|Σ|Δ holds if it is not the case that: all members of Γ have value 1 and all members of Σ have value \(\frac {1}{2}\) and all members of Δ have value 0. While for two-sided sequents these two readings are equivalent, this is not necessarily so for three-sided sequents. In fact, in [22] Ripley offers two proof procedures for S T +, one based on the disjunctive reading and the other on the negative conjunctive reading. Although both systems characterize the same set of valid inferences, they are quite different in many respects. In any case, we think that the disjunctive reading is less cumbersome, and that’s why we use it in this section. However, by appropriately modifying the corresponding definitions, a version of the result we obtain below can be proved for Ripley’s other system as well (unfortunately, substantiating this claim would take too much space).
These rules have the form:

Interestingly, since \(\mathcal {S}\) can be used to represent not only S T + but also \(K_{3}^{+}\) and L P + (all that changes is the definition of validity, the structural and operational rules remain the same), Cut is not admissible for \(K_{3}^{+}\) and L P + either. Cut does become admissible in the proof procedure based on the negative conjunctive reading. Thanks to an anonymous referee for bringing up this issue.
Notice that we can also define proof-theoretic validity for K 3 and other three-valued logics using the system \(\mathcal {S}\). For K 3 the definition would be straightforward. An argument from the set Γ to the set Δ is proof-theoretically-valid in K \(_{3}^{+}\) (notationally, \({\Gamma }\vdash _{K_{3}^{+}}{\Delta }\)) if the sequent Γ|Γ|Δ is provable in \(\mathcal {S}\).
A similar notion was introduced by Avron in [1] to study the properties of certain linear logics (the only difference being that he considers multisets instead of sets). More recently, Mares and Paoli use this notion in [15] to argue in favor of a substructural approach to paradoxes. Finally, Paoli has applied it more specifically to determine the strength of the logic S T + when it is formulated using a two-sided sequent calculus.
Thanks to Francesco Paoli for this definition.
We say that \({\Gamma }\vdash _{TS^{+}}{\Delta }\) if and only if \({\Gamma }|\varnothing |{\Delta }\) is provable in \(\mathcal {S}\).
In order to cope with this and related problems, some supporters of LP-based theories of truth introduce a stronger conditional which validates Modus Ponens.
Thanks to Lavinia Picollo and Thomas Schindler for this argument.
Of course, inferentialism can take many forms, but for now we will work with this vague characterization.
References
Avron, A. (1988). The semantics and proof theory of linear logic. Theoretical Computer Science, 57.
Baaz, M., Fermüller, C., Salzer, G., Zach, R. (1998). Labeled calculi and finite-valued logics. Studia Logica, 61, 7–33.
Baaz, M., Fermüller, C., Zach, R. (1993). Systematic construction of natural deduction systems for many-valued logics. In 23rd international symposium on multiple valued logic, Sacramento, (pp. 208–213). Los Alamitos: IEEE Press.
Beall, J.C. (2009). Spandrels of truth. New York: Oxford University Press.
Beall, J.C., & Murzi, J. (2013). Two flavors of curry’s paradox. Journal of Philosophy, 110(3), 143–165.
Cobreros, P., Egre, P., Ripley, D., van Rooij, R. (2012). Tolerance and mixed consequence in the S’valuationist setting. Studia Logica, 100(4), 855–877.
Cobreros, P., Egré, P., Ripley, D., van Rooij, R. (2012). “Tolerant, Classical, Strict”. Journal of Philosophical Logic, 41(2), 347–385.
Cobreros, P., Egré, P., Ripley, D., van Rooij, R. (2014). Vagueness, truth and permissive consequence. In T. Achourioti et al. (Eds.), Unifying the philosophy of truth. Springer. (forthcoming).
Cobreros, P., Egre, P., Ripley, D., van Rooij, R. (2013). Reaching transparent truth. Mind, 122(488), 841–866.
Field, H. (2008). Saving truth from paradox. Oxford: Oxford University Press.
Hjortland, O. (2014). Verbal disputes in logic: against minimalism for logical connectives. Logique et Analyse, 277, 463–486.
Hjortland, O. (2013). Logical pluralism, meaning-variance, and verbal disputes. Australasian Journal of Philosophy, 91(2), 355–373.
Kripke, S. (1975). Outine of a theory of truth. Journal of Philosophy, 690–716(19).
Leitgeb, H. (2007). What theories of truth should be like (but cannot be). Philosophy Compass, 2(2), 276–290.
Mares, E., & Paoli, F. (2014). Logical consequence and the paradoxes. Journal of Philosophical Logic, 43(2-3), 439–469.
Paoli, F. (2007). Implicational paradoxes and the meaning of logical constants. Australasian Journal of Philosophy, 85(4), 553–579.
Paoli, F. (2003). Quine and Slater on paraconsistency and deviance. Journal of Philosophical Logic, 32, 531–548.
Paoli, F. (2002). Substructural logics: a primer. Dordrecht: Kluwer.
Priest, G. (2006). In contradiction: a study of the transconsistent: Oxford University Press.
Restall, G. (2000). An introduction to substructural logic . Routledge.
Ripley, D. (2013). Paradoxes and failures of cut. Australasian Journal of Philosophy, 91(1), 139–164.
Ripley, D. (2012). Conservatively extending classical logic with transparent truth. Review of Symbolic Logic, 5(2), 354–378.
Rousseau, G. (1967). Sequents in many-valued logic I. Fundamenta Mathematicae, 60, 23–131.
Zardini, E. (2011). Truth without contra(di)ction. Review of Symbolic Logic, 4(4), 498–535.
Acknowledgments
We owe thanks to Norbert Gratzl, Ole Hjortland, Francesco Paoli, Lavinia Picollo, Dave Ripley, Thomas Schindler, and Johannes Stern for very helpful comments on previous versions of this paper. Some of this material was presented at conferences in Barcelona (Logos), Munich (MCMP) and Buenos Aires (Buenos Aires Logic Group). We are very grateful to the members of these audiences for their valuable feedback. We are also specially grateful to Jose Martinez and Elia Zardini for organizing the Substructural Approaches to Paradox Workshop and to Thomas Meier for organizing the 1st MCMP Munich-Buenos Aires Workshop.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Barrio, E., Rosenblatt, L. & Tajer, D. The Logics of Strict-Tolerant Logic. J Philos Logic 44, 551–571 (2015). https://doi.org/10.1007/s10992-014-9342-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-014-9342-6