Abstract
In this paper I will examine what Blaise Pascal means by “infinite distance”, both in his works on projective geometry and in the apologetics of the Pensées’s. I suggest that there is a difference of meaning in these two uses of “infinite distance”, and that the Pensées’s use of it also bears relations to the mathematical concept of heterogeneity. I also consider the relation between the finite and the infinite and the acceptance of paradoxical relations by Pascal.
Similar content being viewed by others
Notes
I would like to thank David Rabouin, Luís César Oliva, Fábio Maia Bertato and Daniel Nagase for reading earlier drafts of this paper. I also would like to thank an anonymous referee for some important remarks. This work was supported by a grant from CNPq.
The notion of infinity appears in almost all mathematical domains which Pascal worked on, including the beginning of probability theory and the manipulations of indivisibles. However, as I am considering the notion of infinite distance, I will restrict myself to projective geometry.
About this, see (Carraud 1992, p. 429): “We can find, especially in the Traité des coniques, a conceptual representation that can account, by analogy, for the paradoxes of infinity with which Pascal deals in the the § 199 [Sel. 230 Laf. 199]. But the research, in the scientific work of Pascal, of representations, patterns, models or analogies, however insightful they are, presupposes a rigorous conceptual continuity between the mathematical texts and the Pensées, a continuity that would be made manifest by the intermediate (and therefore central) position of De l’esprit géométrique. This presupposes therefore that Pascal makes a rigorous use of the concept of infinity in the § 199. But nothing is less certain”. I agree with Carraud in that there is not an absolute continuity between these two periods of Pascal’s work. However, even if this notion suffers a complete reversal in Pascal’s works, this very reversal indicates the necessity of elucidating the role of this notion for Pascal.
I use the term “projective geometry” to designate the works of Desargues and Pascal that would be incorporated into what was later definitively established as projective geometry, without entering in the actual discussions about if these works were already part of projective geometry.
This was done by Taton (1962), and I shall follow him in his analysis of the evolution of Pascal’s work on projective geometry. Other historical details are given by Jean Mesnard in his edition of Pascal’s complete works (Pascal 1970—from now on I quote this edition as OC followed by the number of the volume). In respect to projective geometry, see OC, II, pp. 220–228, 1021–1031, 1102–1108.
As an exception to the enthusiasm for this work there was Descartes, who, after reading Pascal’s work, said that “Before reaching half of it, I judged that he had learned it from M. Desargues, what was confirmed to me immediately afterwards by his own confession”. Letter from Descartes to Mersenne in the 1st or 2nd april 1640. This passage can be found in OC, II, pp. 238–239.
See the comments of J. Mesnard in OC II, pp. 1021–1031. The Academy is a reference to the group of men of science brought together by Le Pailleur in Paris, in succession to Father Mersenne’s group (Mersenne died in 1648). Among the members of the group were Desargues, Roberval, Carcavy and Petit. During the time Mersenne was the head of the group, Pascal’s father, Étienne, attended to it, and Le Pailleur was also a friend of Pascal’s family. The letter, called after its dedicatory, Celleberrimae Matheseos Academiae Parisiensi, can be found in OC, II, pp. 1031–1035. It should be noted that in fact the Latin title refers to a mathematical academy, and not a scientific one.
Leibniz relates that its original title was Generatio conisectionum, tangentium et secantium; seu projectio peripheriae, tangentium, et secantium circuli in quibuscumque oculi, plani ac tabellae positionibus, that is, Generation of Conics, Tangents, and Secants; or the Projection of the Circumference, Tangents and Secants of the Circle for Every Position of the Eye, of the Plane and of the Picture Plane. See OC, II, p. 1108.
See Mesnard (1994, p. 98).
A comparison between Desargues’ and Descartes’ styles of geometry can be found in Granger (1968).
See Taton (1962), p. 207. Pascal quotes the Conics of Apollonius in the 1654 letter to the academy.
See the commentary by Mesnard in OC, II, p. 221.
See Taton (1962, p. 207).
For the originality of Pascal’s unified perspective, see Taton (1962, pp. 235–240).
See the work of Field (1994, pp. 220–221), who notes that Mersenne’s Harmonie universelle presents a diagram of the system of conics that seems to be a reproduction of the one found in Kepler’s Ad Vitellionem paralipomena, even if Mersenne does not make explicit his source and neither does appropriate the whole of Kepler’s treatment of the conics, not accepting neither the analogies among the conics neither the points at infinity.
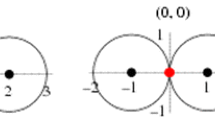
Some other examples are the 3rd definition, that says that two or more lines are concurrent if they intersect at the same point, at finite or infinite distance (ad distantiam vel finitam, [...] vel infinitam); the 5th definition, that defines an asymptote line as an infinite line conducted on the plane of a conic, that does not meet the conic except at an infinite distance (nisi ad distantiam infinitam); and the remark that asymptotes should be considered as tangents at an infinite distance (ad distantiam infinitam) (first scholium of the last corollary).
OC, II, pp. 1112–1113. The translation of tabella and apparentia is by no means simple. Tabella reminds the vocabulary of painting and, more precisely, that of perspective, in which the canvas was considered to be an intersection between the eye and the object represented. I have opted for translating tabella by “picture plane”, and we should keep in mind that in this passage Pascal defines tabella as the plane located between the “eye” (oculus) and what is projected (in this case, the circumference of the circle). In this respect, see Magnard (2007, pp. 70–71). In respect to apparentia, possible translations are “visible form” and “figure”, but I have opted for “image” for reminding that in this case it is the projection of the circle.
The passage is of the scholium of the third corollary of the sixth definition (OC, II, pp. 1114).
OC, II, p. 231.
See Taton (1962, p. 202).
I use “symbol” here to mean that one concept stands for another. Pascal’s French is figure, that appears for instance in fragment Sel. 339, Laf. 308. In this context, figure is connected to the relation of figuration that comes from biblical exegesis.
See Mesnard (1994, p. 93), and Mesnard’s comment in OC, II, p. 1102.
The dating of this writing is not precise, but it is probably from 1655 (cf. OC, II, pp. 368–376), that is, probably subsequent to the works on projective geometry, which Pascal seems to have developed until 1654.
OC, III, p. 408. In Heath’s translation (Euclid 1956) we read: Definition 3: “A ratio is a sort of relation in respect of size between two magnitudes of the same kind [homogenôn]” and definition 4: “Magnitudes are said to have a ratio to one another which are capable, when multiplied, of exceeding one another”. I use “genus” to translate Pascal’s French genre (in works written in Latin, Pascal writes genus). In definition V, 3 we found the term homogenôn, usually translated as “of the same kind”. I have preferred to use “genus”, but we should understand it in its mathematical technical meaning, and not as related to the biological or sociological meaning of “family” or “group”, possible translations of Greek génos.
OC, II, pp. 1271–1272.
Pascal seems to have a preference for writing “ordre” instead of “genre” in his later writings.
The definition of this solid is the following: “Definition. If one rotates a hyperbola around an asymptote, as around an axis, one generates a solid infinite in length [longitudine infinitum] in the direction of the axis, which we call an acute hyperbolic solid” (Torricelli, De solido hyperbolico acuto, in Mancosu (1996, p. 132).
See Mancosu (1996, p. 136).
Torricelli, De solido hyperbolico acuto, in Mancosu (1996, p. 134). Mancosu makes an important remark: “When Torricelli says that none of the lateral surfaces have an infinite length, he means that none of them has an infinite area”. This would be confirmed by later writings by Torricelli.
The assertion that there is no proportion between the finite and the infinite was already formulated by Aristotle in De caelo, I, 6, 274a. It should be noted, however, that Saint Thomas’ assertion, in a theological context, is not bidirectional: from the fact that man (finite) is not proportional to God (infinite), it does not follow that God is not proportional to man.
“Ces deux infinis, quoique infiniment différents, sont néanmoins rélatifs l’un à l’autre, de telle sorte que la connaissance de l’un mène nécessairement à la connaissance de l’autre” (OC, III, p. 410).
Translation by O. W. Wright (Pascal 1909). Pascal assumes in this example that the earth is flat, as the Logic of Port-Royal already noted. Cf. OC III, p. 411, note by J. Mesnard.
See Magnard (2007, p. 71).
The fact that the extremes touch one another appears not only in projective geometry, but also in several passages of the Pensées. In fragment Sel. 117, Laf. 83, for instance, we read that “The sciences have two extremes, which meet”. In this case, the two extremes are our natural ignorance and the wise ignorance of those who, after exploring human knowledge, realize they know nothing. Besides the mathematical motivation for talking about the coexistence of contraries and the theological reasons for it, it would be necessary to analyze the relation to Neoplatonic thought, and, closer to Pascal, Cusanus’ work on the coincidentia oppositorum. I will not develop this aspect here.
Granger (1968, p. 57).
In Taton (1951, p. 99).
The question of the mathematical status of elements at infinity according to Desargues is a complex one. The difficulty of introducing points at infinity seems to have been acknowledged by Desargues himself in the Advertissement at the end of his Brouillon Projet, as noted by Field (1994, p. 226), Desargues introducing the comparison “comme” (“as if”) in several passages. The elements at infinity are not tacitly accepted anymore, but the difficulties concerning them are taken into account as they are presented as hypothetical entities. Thus in the beginning of the text Desargues proposes that lines of the same ordonnance are either concurrent or parallel to one another, and in both cases these lines converge to the same place (“qu’en l’une aussi bien qu’en l’autre de ces deux espèces de position elles tendent toutes à un mesme endroict”), but in the Advertissement “we are told to add ‘comme’ between ‘tendent’ and ‘toutes’, thereby changing the sense to ‘... it is as if they all converged to the same place’ ” ((Field 1994, p. 226)). On the other hand, the two infinities seem somehow essential in Desargues’s thought about mathematics, and, as Bkouche (1991) notes, the elements at infinity could not work just at a formal level. As I will argue, for Pascal there seems to be an acceptance of the existence of these paradoxical elements.
This phrase was used by many authors in the medieval period. In spite of that, Pascal’s use of it is somewhat original: while many authors talked about God as an infinite sphere, in this fragment we can understand that Pascal is talking about nature as an infinite sphere.
Notably Descartes made the question explicit, but it can be found also in other philosophers, as Pascal and Leibniz–in this respect, see Serres (1968, pp. 657–664). Perspective has a fundamental importance here for Pascal, as was also observed by Mesnard (1994, pp. 94–99). As both these scholars remark, Desargues has formulated the question about the existence of a fixed point in terms of perspective and geometry of conics, and Pascal discuss this model’s philosophical meaning. In this respect, see fragment Sel. 55, Laf. 21: “(...) If we look at our work immediately after completing it, we are still too much involved in it; too long afterwards and we cannot pick it up again. Similarly with pictures seen from too far off, or from too close up. And there is only one indivisible point which is the right place. The other are too close, too distant, too high, or too low. Perspective determines it in the art of painting. But in truth and morality who will determine it?”.
Pascal is thus saying, on the one hand, that the position of God is where both infinities meet, and, on the other hand, that Christ occupies the center of everything. God as creator and Christ as the incarnation of God are both represented by a geometrical meaning, but not exactly the same one.
References
Bkouche, R. (1991). La naissance du projectif - de la perspective à la géométrie projective. In R. Rashed (Ed.), Mathématiques et philosophie de l’antiquité à l’âge classique. Paris: Éditions du centre nationel de la recherche scientifique.
Carraud, V. (1992). Pascal et la philosophie. Paris: PUF.
Euclid (1956). The thirteen books of the elements. (Sir Thomas L. Heath, Trans.). New York: Dover.
Field, J. V. (1994). The infinitely great and the infinitely small in the work of girard desargues. In J. Dhombres & J. Sakarovitch (Eds.), Desargues en son temps. Paris: A. Blanchard.
Gardies, J.-L. (1984). Pascal entre Eudoxe et Cantor. Paris: Vrin.
Granger, G.-G. (1968). Essai d’une Philosophie du Style. Paris: Armand Colin.
Hara, K. (1984). Nouvelles observations sur les écrits mathématiques de pascal. Historia Scientiarum, 26, 1–17.
Magnard, P. (1992). La pensée moderne à l’épreuve de l’infini. In Monnoyeur (ed.). Infini des mathématiciens, infini des philosophes. Paris: Belin.
Magnard, P. (2007). Pascal. La clé du chiffre. Paris: La table ronde.
Mancosu, P. (1996). Philosophy of mathematics and mathematical practice in the seventeenth Century. New York: Oxford University Press.
Mesnard, J. (1994). Desargues et pascal. In J. Dhombres & J. Sakarovitch (Eds.), Desargues en son temps. Paris: A. Blanchard.
Pascal, B. (1909). Of the geometrical spirit. In: Pascal. Minor works. (O. W. Wright, Trans.). Harvard Classics, Vol. 48, Part 3. 1909–14. Web edition published by eBooks@Adelaide avaiable in http://ebooks.adelaide.edu.au/p/pascal/blaise/geom/
Pascal, B. (1970). Oeuvres complètes. Text established, presented and noted by Jean Mesnard. Paris: Desclée de Brouwer. Volumes II (1970), III (1991) et IV (1992). (Referred to as OC).
Pascal, B. (1995). Pensées and other writings. (Honor Levi, Trans.). New York: Oxford University Press.
Pascal, B. (2000). Pensées. Text established by Phillipe Sellier. Presented and noted by Gérard Ferreyrolles. Paris: Le livre de poche.
Serres, M. (1968). Le système de Leibniz et ses modèles mathématiques. Paris: P.U.F.
Taton, R. (1951). L’oeuvre mathématique de G. Desargues. Paris.
Taton, R. (1962). L’oeuvre de pascal en géométrie projective. Revue d’histoire des sciences et de leurs applications Tome, 15(3–4), 197–252.
Acknowledgments
The financial support was done by CNPq.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cortese, J.F.N. Infinity between mathematics and apologetics: Pascal’s notion of infinite distance. Synthese 192, 2379–2393 (2015). https://doi.org/10.1007/s11229-014-0599-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-014-0599-7