Abstract
According to the present pluralism in mathematical logic, I translate from classical logic to non-classical logic the predicates of the classical square of opposition. A similar unique structure is obtained. In order to support this new logical structure, I investigate on the rich legacy of the non-classical arguments presented by ingenuity by several authors of scientific theories. A comparative analysis of their ways of arguing shows that each of these theories is severed in two parts; the former one proves a universal predicate by an ad absurdum proof. This conclusion of every theory results to be formalised by the A thesis of the new logical structure. Afterwards, this conclusion is changed in the corresponding affirmative predicate, which in the latter part plays the role of a new hypothesis for a deductive development. This kind of change is the same suggested by Leibniz’ principle of sufficient reason. Instead, Markov’s principle results to be a weaker logical change, from the intuitionist thesis I in the affirmative thesis I. The relevance of all the four theses of the new logical structure is obtained by studying all the conversion implications of intuitionist predicates. In the Appendix, I analyse as an example of the above theories, Markov’s presentation of his theory of real numbers.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
The last instance of this qualification is the otherwise excellent text by [23].
- 2.
- 3.
Let us recall that the relationships of an affirmative proposition of propositional classical logic with the corresponding DNS of intuitionist logic is assured by a well-known theorem on their relationship—i.e. once a formula A is true in classical logic, then evenly ¬¬A is true in the latter logic. Instead, to translate a DNSs in an affirmative sentences, owing to the failure of the law of the double negation, is a problematic move [41, 56ff]. Notice also that in intuitionist logic an ad absurdum proof ends by a DNS; to change it in an affirmative sentence is allowed by classical logic only [18, p. 27].
- 4.
[41, pp. 57–59]. In a previous paper [12] I introduced a square of opposition including at the same time two classical predicates (the theses A and E) and two non-classical predicates (the theses I and O) which differ from the traditional ones because the copula ‘is’ is changed in ‘it is not true that it is not’, or ‘is
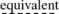 ’; this addition of double negations is not enough to represent one of the above-mentioned translations; however the results of the Sects. 7 and 8 of this paper agree with the above-mentioned translations.
’; this addition of double negations is not enough to represent one of the above-mentioned translations; however the results of the Sects. 7 and 8 of this paper agree with the above-mentioned translations. - 5.
According to modern logicians Aristotle’ square of opposition did not take in account the existential import of the theses. A more accurate investigation by authoritative scholars showed that instead Aristotle did it [33].
- 6.
The same translations hold true for minimal predicate logic, i.e. when the logical law ex falso quodlibet (P→(¬P→Q), where P and Q are whatsoever predicates) is weakened in the law P→(¬P→¬Q), hence the latter logic is strictly weaker than intuitionist logic [41, p. 57]. One may guess that an experimental scientist is not allowed to deduce ex falso everything, included the true; but the false only; hence, his logic is the minimal one. In such a case the above translations in minimal predicate logic give distinct results from those in intuitionist logic when one claims that the copula “is” of a thesis of SO is better translated in logical terms by an equivalence, i.e. a double implication. In such a case the three translations of the theses of SO in minimal predicate logic are not equivalent in both E and I theses. However, according to the next footnote 18, the following results seem hold true for the minimal SO-like too even in the latter case.
- 7.
- 8.
In the past, this way of arguing joining together the DNSs was ignored. Rather some philosophers argued by considering at the same time the three values of a sole proposition A, i.e. A, ¬A and
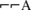 . Cusanus claimed to argue through an opposite’s coincidence of A and
. Cusanus claimed to argue through an opposite’s coincidence of A and 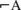 ; Hegel through an almost mechanical addiction of a negation to a
; Hegel through an almost mechanical addiction of a negation to a 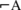 sentence. See my paper [15].
sentence. See my paper [15]. - 9.
It is by appealing to the past experiences of scientific theories that I improved the unsuccessful Beth’s research for a non-deductive way of organising a mathematical theory [2]. D’Alembert first stressed that there exists two kinds of theory organisation; he suggested that, beyond the “rational” kind, an “empirical” one exists [6]. Subsequently, for illustrating these two different models L. Carnot devoted two pages of each his two books on mechanics [3, 4]; he claimed to develop his theory in an “empirical” way. In past century both H. Poincaré [34, 35] and independently A. Einstein again suggested two similar kinds of theory organisation [27, 32].
- 10.
Some of the above-mentioned authors wrote texts which are less structured in logical terms; e.g. L. Carnot’s calculus, Lavoisier’s chemistry, Galois’ theory of groups, Klein’s Erlangen program, Einstein’s theory of special relativity all lack of ad absurdum theorems.
- 11.
[29]. Here and in the following, emphasis is added for manifesting to the reader the two negations within a doubly negated sentence.
- 12.
[30, Proposition 19]. This book was analysed through its DNSs by my paper [14]. Lobachevsky’s main text puts the problem of how much parallel lines to a straight line exist. In order to obtain evidence for his guess—i.e. two parallel lines—he proves through DNSs five theorems, most of which are ad absurdum theorems. At the end of the prop. 22, shown by an ad absurdum theorem, he concludes that his supposition with respect to Euclid’s hypothesis, receives an equivalent evidence in both all points and in all figures in the space.
- 13.
[5, p. 23]. S. Carnot’s thermodynamics puts the problem of the maximum efficiency in the heat/work conversions; in order to solve it, he looks for a new method by arguing through DNSs about his celebrated cycle of four transformations. The list of DNSs ends by means of his well-known ad absurdum theorem about the maximum efficiency in all heat/work conversions. Carnot’s book was analysed through its DNSs by the paper [17].
- 14.
[36, p. 187]. Poincaré criticism to Formalists’ attempt to prove by finitist means the principle of mathematical induction concludes by essentially the following DNS: “… does not exist contradiction” for all entire numbers. The current version of this principle changes it in the corresponding affirmative predicate. See my paper [7].
- 15.
[28]. Kolmogorov’s foundation of the minimal logic argues by means DNSs and an ad absurdum theorem stating the above conclusion. Afterwards, Kolmogorov thinks that nothing opposes to always deductively argue by means of pseudotruths from the axioms of the type A of Hilbert’s formalisation of logic. See also [10].
- 16.
[1, p. 58]. The subsequent sentence (“Hence, it is necessary thus to admit that [there it is not true that do not exist] there exist simple relationships also among the volumes of [all] the gaseous substances and the number of the simple or composed molecules which compose them) constitutes the celebrated “Avogadro’s law” on the molecular constitution of whatsoever kind of matter. An analysis of the paper through its DNSs is given by [16].
- 17.
Reference [20] studies a similar problem in various kinds of logic, but at the propositional level only.
- 18.
Remarkably, Agkq is the same in both minimal logic and intuitionist logic. Notice that one may guess that when an author of a PO theory obtains, by arguing in minimal logic, the universal predicate Agkq, he governs by this final DNS the entire universe of his logical arguing with respect to the basic problem. At this stage, he, when meeting a false sentence, can consider it as belonging to a purely theoretical universe; hence, he can apply the intuitionist law on the false, according to which everything of this theoretical universe follows from it. In other words, when he achieves this predicate, at the same time he implicitly changes the kind of logic from the minimal one to the intuitionist one.
- 19.
- 20.
The two requirements on the predicate on which MP is applied suggests that PRS° would have to be applied according to the same requirements, i.e. on a predicate which is decidable one and it is obtained as the result of an ad absurdum theorem. Such requirements surely would avoid all criticisms to the application of PSS°, first of all the criticism to be a metaphysical principle. In the past, a great debate aimed to clarify the use of the PSR°. From the above we conclude that PSR is not a heuristic principle for validating a mere guess on an isolated event, but an architectural principle, to be applied to an entire PO theory (see my paper [9]). Its theory-dependence explains why in the ancient times, when an analysis on PO theories was premature, it was ignored; and why in modern times, when scholars devoted little attention to both non-deductive theories and non-classical logic, it was misinterpreted.
- 21.
- 22.
It is just after a chain of ad absurdum proofs (propositions nos. 17–22) that Lobachevsky stated the existence of two parallel lines, conceived as ever more prolonged segments, as an alternative hypothesis to the Euclidean one. Markov’s two requirements enlightens the implicit requirements of the common move performed by all the above authors of a PO theory, which of course concerns a method which has to rely on decidable predicates; also the common move occurring at the end of the former parts of OP theories is implicitly justified by not having reason for excluding the affirmative conclusion. Moreover, notice that the same implicit ad absurdum argument that justifies PRS° holds true for Markov’s move: “… otherwise the reality is absurd”.
- 23.
Also Markov states that by means of the DNSs nos. 32, 33, 34.
References
Avogadro, A.: Essay d’une manière de determiner les masses relatives des molecules élémentaires des corps…J. Phys. Chim. Hist. Nat. 73, 58–76 (1811)
Beth, E.W.: Foundations of Mathematics, ch. I, 2. Harper, New York (1959)
Carnot, L.: Essai sur le machines en général, pp. 101–103. Defay, Dijon (1783)
Carnot, L.: Principes de l’équilibre et du mouvement, pp. xii–xv. Deterville, Paris (1803)
Carnot, S.: Réflexions sur la puissance motrice du feu, p. 23. Blanchard, Paris (1824)
Le Ronde d’Alembert, J.: Elémens. In: Le Ronde d’Alembert, J., Diderot, D. (eds.) Éncyclopédie Française, p. 17 (1754)
Drago, A.: Poincaré vs. Peano and Hilbert about the mathematical principle of induction. In: Greffe, J.-L., Heinzmann, G., Lorenz, K. (eds.) Henri Poincaré. Science et Philosophie, pp. 513–527. Blanchard/Springer, Paris/Berlin (1996)
Drago, A.: Mathematics and alternative theoretical physics: the method for linking them together. Epistemologia 19, 33–50 (1996)
Drago, A.: The birth of an alternative mechanics: Leibniz’ principle of sufficient reason. In: Poser, H., et al. (eds.) Leibniz-Kongress. Nihil Sine Ratione, vol. I, pp. 322–330. Berlin (2001)
Drago, A.: A.N. Kolmogoroff and the relevance of the double negation law in science. In: Sica, G. (ed.) Essays on the Foundations of Mathematics and Logic, pp. 57–81. Polimetrica, Milano (2005)
Drago, A.: Four ways of logical reasoning in theoretical physics and their relationships with both the kinds of mathematics and computer science. In: Cooper, S.B., et al. (eds.) Computation and Logic in Real World, pp. 132–142. Univ. Siena Dept. of Math. Sci., Siena (2007)
Drago, A.: The square of opposition and the four fundamental choices. Logica Univers. 2, 127–141 (2008)
Drago, A.: Lo scritto di Einstein sulla relatività. Esame secondo il modello di organizzazione basata su un problema. Atti Fond. G. Ronchi 64, 113–131 (2009)
Drago, A.: A logical analysis of Lobachevsky’s geometrical theory. Atti Fond. G. Ronchi 64(4), 453–481 (2010). Italian version in: Period. Mat., Ser. VIII 4, 41–52 (2004)
Drago, A.: The coincidentia oppositorum in Cusanus (1401–1464), Lanza del Vasto (1901–1981) and beyond. Epistemologia 33, 305–328 (2010)
Drago, A., Oliva, R.: Atomism and the reasoning by non-classical logic. Hyle 5, 43–55 (1999)
Drago, A., Pisano, R.: Interpretation and reconstruction of Sadi Carnot’s Réflexions through non-classical logic. Atti Fond. G. Ronchi 59, 615–644 (2004). Italian version in: G. Fis. 41, 195–215 (2000)
Dummett, M.: Principles of Intuitionism. Clarendon, Oxford (1977)
Einstein, A.: Zur Elektrodynamik bewegter Koerper. Ann. Phys. 17, 891–921 (1905)
Gabbey, D., Olivetti, N.: Goal-oriented deductions. In: Gabbey, D., Guenthner, F. (eds.) Handbook of Philosophical Logic, vol. 9, pp. 134–199. Reidel, Boston (2002)
Goedel, K.: Collected Works, papers 1932 and 1933f. Oxford University Press, Oxford (1986)
Grize, J.B.: Logique. In: Piaget, J. (ed.) Logique et connaissance scientifique. Éncyclopédie de la Pléiade, pp. 135–288 (206–210). Gallimard, Paris (1970)
Haak, S.: Deviant Logic. Oxford University Press, Oxford (1978)
Hand, M.: Antirealism and Falsity. In: Gabbey, D.M., Wansing, H. (eds.) What is Negation?, pp. 185–198 (188). Kluwer, Dordrecht (1999)
Heyting, A.: Intuitionism. An Introduction, Sect. 2. North-Holland, Amsterdam (1971)
Kleene, C.: Introduction to Metamathematics, pp. 318–319. Van Nostrand, Princeton (1952)
Klein, M.J.: Thermodynamics in Einstein’s thought. Science 57, 505–516 (1967)
Kolmogorov, A.N.: On the principle ‘tertium non datur’. Mat. Sb. 32, 646–667 (1924/1925). Engl. translation in: van Heijenoorth, J. (ed.) From Frege to Goedel, pp. 416–437. Harvard University Press, Cambridge (1967)
Leibniz, G.W.: Letter to Arnauld, 14-7-1686, Gerh. II, Q., Opusc. 402, 513
Lobachevsky, N.I.: Geometrische Untersuchungen zur der Theorien der Parallellineen. Finkl, Berlin (1840). Engl. translation as an Appendix to: Bonola, R.: Non-Euclidean Geometry. Dover, New York (1955)
Markov, A.A.: On constructive mathematics. Tr. Mat. Inst. Steklova 67, 8–14 (1962). Also in: Am. Math. Soc. Transl. 98(2), 1–9 (1971)
Miller, A.I.: Albert Einstein’s Special Theory of Relativity, pp. 123–142. Addison-Wesley, Reading (1981)
Parsons, T.: Things that are right wit the traditional square of opposition. Logica Univers. 2, 3–11 (2008)
Poincaré, H.: La Science et l’Hypothèse, Ch. “Optique et Electricité”. Hermann, Paris (1903)
Poincaré, H.: La Valeur de la Science, Ch. VII. Flammarion, Paris (1905)
Poincaré, H.: Science et Méthode, p. 187. Flammarion, Paris (1912)
Prawitz, D.: Meaning and proof. The conflict between classical and intuitionist logic. Theoria 43, 6–39 (1976)
Prawitz, D., Melmnaas, P.-E.: A survey of some connections between classical intuitionistic and minimal logic. In: Schmidt, A., Schuette, H. (eds.) Contributions to Mathematical Logic, pp. 215–229. North-Holland, Amsterdam (1968)
Tennant, N.: Natural Logic, p. 57. Edinburgh University Press, Edinburgh
Troesltra, A.: Remarks on intuitionism and the philosophy of mathematics. In: Costantini, D., Galavotti, M.C. (eds.) Nuovi Problemi della Logica e della Filosofia della Scienza, pp. 211–228 (223). CLUEB, Bologna (1991)
Troelstra, A., van Dalen, D.: Constructivism in Mathematics, vol. 1. North-Holland, Amsterdam (1988)
van Dalen, D.: Intuitionist logic. In: Gabbey, D.M., Guenthner, F. (eds.) Handbook of Mathematical Logic, vol. II, pp. 225–449 (226 and 230). Reidel, Dordrecht (2002)
Woods, J., Irvine, A.: Aristotle’s early logic. In: Gabbey, D.M., Woods, J. (eds) Handbook of History of Logic, vol. 1, pp. 27–99 (66). Elsevier, New York (2004)
Acknowledgements
I acknowledge two anonymous referees for an improvement of my previous logical framework, and David Braithwhaite for the correction on my English text.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: The analysis through the double negations of [31]
Appendix: The analysis through the double negations of [31]
Notice that modal words are equivalent, via S4 translation, to DNSs; these words are wave underlined.
-
(1)
Recently the constructive trend in mathematics has been significantly developed. Its goal is to base all investigations on constructive objects and to carry them out within the bounds of the abstraction of potential realizability and without use of the abstraction of actual (= not potential) infinity; …
-
(2)
… it rejects the so-called pure existence [= not constructive] theorems, …
-
(3)
… since the existence of an object with given properties is considered proved only when a
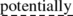 realizable method for the construction of an object with those properties bas been indicated … .
realizable method for the construction of an object with those properties bas been indicated … . -
(4)
… We do not define the concept of a constructive object, but rather
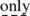 clarify it.
clarify it. -
(5)
In constructive mathematical theories we limit ourselves to the consideration of constructive objects of some standard type, which frees us from the necessity of formulating a general definition of a constructive object.
-
(6)
The abstraction of identity is used here in a natural way; we identify the words (1) and (2); we abstract away from their having any differences; we say that they are the same word … .
-
(7)
… When considering words in a given alphabet we are forced into an abstraction of another kind—into the abstraction of potential existence … .
-
(8)
… It consists in abstracting away from the practical limits of our possibilities in space, time and material when it comes to the existence of words … .
-
(9)
… We cannot write on a given blackboard of a given dimension words of arbitrary [= unlimited] length … .
-
(10)
… We abstract away from this practical impossibility and begin to argue as if this were possible.
-
(11)
This does not at all mean that we begin to consider the “sequence of naturals” as an infinite “object.” …
-
(12)
… Such a consideration would involve an abstraction of an actual infinity, …
-
(13)
… taking us beyond the limits of constructive mathematics and into something characteristic of the so-called “classical” mathematics.
-
(14)
In “classical” mathematics there have been many “pure existence theorems,” which consist in assertions about the “existence” of objects with certain properties even despites a complete ignorance of means to construct such an object.
-
(15)
Constructive mathematics rejects such propositions [on pure existence] …
-
(16)
… In constructive mathematics the existence of an object with certain properties is
 considered proved when a potentially realizable method has been given for the construction of an object with the given properties.
considered proved when a potentially realizable method has been given for the construction of an object with the given properties. -
(17)
This understanding of disjunction does not permit one to take as true the law of the excluded middle: “P or not P.”…
-
(18)
…2. The formulation and development of the constructive trend took place on the basis of work that appeared in the 1930s which made precise the concept of an algorithm, freeing this concept from vagueness and subjectivity… .
-
(19)
As we know, this vague concept of a was made precise in the 30s in the work of several men, who took different approaches: Church, Kleene, Turing, Post. The theories constructed by these men—Kleene’s theory of recursive functions, Church’s calculus of λ-conversion, the theory of Turing machines and Post’s theory of finite combinatory processes—turned out to be
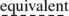 to one another and to lead to essentially the same formulation of the concept of an algorithm …
to one another and to lead to essentially the same formulation of the concept of an algorithm … -
(20)
… New formulations of this concept, also
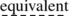 to the previous ones, were constructed one after another by other authors, …
to the previous ones, were constructed one after another by other authors, … -
(21)
… and even in the present time new theories of algorithms are continually being published that are
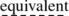 to the previous theories … .
to the previous theories … . -
(22)
… It is not
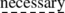 for us at this time to look into these theories to try to find the best one.
for us at this time to look into these theories to try to find the best one. -
(23)
The algorithm also determines the end of the procedure which
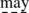
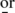
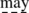
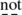 occur.
occur. -
(24)
The theory of normal algorithms is constructed which in the framework of abstract
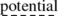 existence … .
existence … . -
(25)
… The words in the alphabet A under consideration and the schemes of the normal algorithms in A are
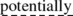 realizable constructive objects … .
realizable constructive objects … . -
(26)
… The procedure itself of applying a normal algorithm to a given word is considered by us to be a
 realizable procedure.
realizable procedure. -
(27)
I consider it [is]
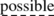 to apply here an argument “by contradiction”,
to apply here an argument “by contradiction”, -
(28)
… i.e. to assert that the algorithm A is applicable to the word P if the assumption that the process of applying A to P continues indefinitely leads to a contradiction.
-
(29)
If I defend this means of argument here, it is not because I find it without error according to my intuition, …
-
(30)
… but rather, firstly, because I see no reasonable reason for rejecting it, …
-
(31)
… and secondly, because arguments of this type make it
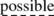 to construct a constructive mathematics that is well able to serve contemporary natural Science … .
to construct a constructive mathematics that is well able to serve contemporary natural Science … . -
(32)
… I insist that this does not go beyond the bounds of the constructive direction: …
-
(33)
… the abstraction of actual infinity is not made, …
-
(34)
… existence continues to coincide with a
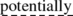 realizable construction …
realizable construction … -
(35)
… If we assert on the basis of the proved impossibility of the indefinite continuation of a given procedure that this procedure ends, then this yields a perfectly well-defined method of construction: continue the process until its completion … .
-
(36)
… The circumstance that the number of steps cannot be bounded “in advance”, here changes nothing of importance … .
-
(37)
… It is even
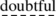 that the requirement that this number be bounded in advance will ever be formulated precisely and objectively … .
that the requirement that this number be bounded in advance will ever be formulated precisely and objectively … . -
(38)
… It is not difficult to see that this method for proving the applicability of an algorithm …
-
(39)
…
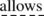 one to justify the following method of argument … .
one to justify the following method of argument … . -
(40)
… Let P a property, ad let there be an algorithm that decide for every natural number n whether or not n has the property P. If the proposition that no number has the property P leads to a contradiction there is a natural number with the property P.
The analysis of this list of DNS is easy. The list presents one only ad absurdum proof; it is exposed wordily by the DNSs 29 and 30. Hence, there is one unit of arguing only. The following DNSs are aimed to illustrate the result obtained. After the DNS 40 the development of the theory assumes the last DNS as a new hypothesis.
Rights and permissions
Copyright information
© 2012 Springer Basel
About this chapter
Cite this chapter
Drago, A. (2012). Pluralism in Logic: The Square of Opposition, Leibniz’ Principle of Sufficient Reason and Markov’s Principle. In: Béziau, JY., Jacquette, D. (eds) Around and Beyond the Square of Opposition. Studies in Universal Logic. Springer, Basel. https://doi.org/10.1007/978-3-0348-0379-3_12
Download citation
DOI: https://doi.org/10.1007/978-3-0348-0379-3_12
Publisher Name: Springer, Basel
Print ISBN: 978-3-0348-0378-6
Online ISBN: 978-3-0348-0379-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


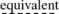 ’; this addition of double negations is not enough to represent one of the above-mentioned translations; however the results of the Sects.
’; this addition of double negations is not enough to represent one of the above-mentioned translations; however the results of the Sects. 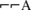 . Cusanus claimed to argue through an opposite’s coincidence of A and
. Cusanus claimed to argue through an opposite’s coincidence of A and 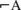 ; Hegel through an almost mechanical addiction of a negation to a
; Hegel through an almost mechanical addiction of a negation to a 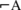 sentence. See my paper [
sentence. See my paper [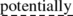 realizable method for the construction of an object with those properties bas been indicated … .
realizable method for the construction of an object with those properties bas been indicated … .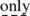 clarify it.
clarify it. considered proved when a potentially realizable method has been given for the construction of an object with the given properties.
considered proved when a potentially realizable method has been given for the construction of an object with the given properties.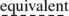 to one another and to lead to essentially the same formulation of the concept of an algorithm …
to one another and to lead to essentially the same formulation of the concept of an algorithm …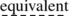 to the previous ones, were constructed one after another by other authors, …
to the previous ones, were constructed one after another by other authors, …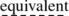 to the previous theories … .
to the previous theories … .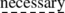 for us at this time to look into these theories to try to find the best one.
for us at this time to look into these theories to try to find the best one.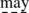
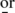
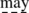
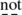 occur.
occur.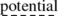 existence … .
existence … .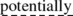 realizable constructive objects … .
realizable constructive objects … . realizable procedure.
realizable procedure.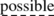 to apply here an argument “by contradiction”,
to apply here an argument “by contradiction”,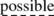 to construct a constructive mathematics that is well able to serve contemporary natural Science … .
to construct a constructive mathematics that is well able to serve contemporary natural Science … .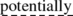 realizable construction …
realizable construction …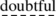 that the requirement that this number be bounded in advance will ever be formulated precisely and objectively … .
that the requirement that this number be bounded in advance will ever be formulated precisely and objectively … .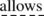 one to justify the following method of argument … .
one to justify the following method of argument … .