Abstract
The development of causal modelling since the 1950s has been accompanied by a number of controversies, the most striking of which concerns the Markov condition. Reichenbach's conjunctive forks did satisfy the Markov condition, while Salmon's interactive forks did not. Subsequently some experts in the field have argued that adequate causal models should always satisfy the Markov condition, while others have claimed that non-Markovian causal models are needed in some cases. This paper argues for the second position by considering the multi-causal forks, which are widespread in contemporary medicine (Section 2). A non-Markovian causal model for such forks is introduced and shown to be mathematically tractable (Sections 6, 7, and 8). The paper also gives a general discussion of the controversy about the Markov condition (Section 1), and of the related controversy about probabilistic causality (Sections 3, 4, and 5).










Similar content being viewed by others
Notes
For definitions of the Markov condition, and the other technical terms used in this paper, see appendix.
There are actually two senses of ‘objective’ as applied to probability. ‘Objective’ can mean objective in the scientific sense, or objective in the logical, or epistemic, sense. In this paper, we will confine ourselves to probabilities, which are objective in the scientific sense. For probabilities, which are objective in the logical, or epistemic, sense, see Williamson 2005, Ch. 5, pp. 65–106, and Williamson 2010.
On pp. 51–57 of his 2005, Williamson is actually discussing exceptions to what he calls the Causal Markov Condition, which is defined on p. 50, and is distinguished from the Markov Condition, which is defined on p. 15. In this paper, we are using the term ‘Markov condition’ to cover both what Williamson calls the ‘Markov condition’ and what he calls the ‘Causal Markov Condition’. So on pp. 51–57 of his 2005, Williamson is indeed discussing what are exceptions to the Markov condition in our sense of the term. The differences here are purely terminological.
In speaking of statistical tests confirming that the Markov condition holds, we do not mean to imply that they establish the Markov condition with certainty, but only that they provide some evidence in its favour. A scientific conjecture can never be established with certainty by a number of tests with favourable outcomes, since future tests may always show that the conjecture is false in some respects.
The terminology ‘type/token’ is often used for the distinction, which we have described as ‘generic/single-case’. Russo and Williamson argue that generic/single-case is a better terminology than type/token, since the terms ‘type’ and ‘token’ normally refer to objects, whereas causal claims characteristically relate events and variables (see Russo (2009) and Russo and Williamson (2011)). We are sympathetic to their point of view and will use generic/single-case, except when quoting from authors who use type/token. Hitchcock (2010, 1.3) uses ‘general/singular’ for the same distinction.
For details, see Codell Carter (2003).
It might be objected that Fig. 4 is not appropriate as a model for the Hesslow example, since in this case X, i.e. taking the pill has a causal influence on Y, i.e. pregnancy. So an arrow should be added, joining X to Y, as in Fig. 7. We will discuss this possibility in Section 5, but leave it aside for the moment.
A good recent discussion of Simpson’s Paradox is to be found in Bandyoapdhyay et al. (2011).
Our formulation of CP2 given above is an example of this.
This remark may seem exaggerated. Yet there are many learned and highly mathematical papers published in leading journals which devote themselves to constructing models for fantasy examples such as ‘A spell cast by Merlin caused the prince to turn into a frog.’ In our view such work is valueless. Clearly in the real world spells do not cause princes to turn into frogs. Why should causality, as imagined in such a fantasy world, have anything to do with causality in the real world? Causal modellers should devote themselves to genuine scientific examples, which arise in the real world. There are a rich variety of these, and there is consequently no need to bring in the consideration of purely imaginary examples.
An informal summary of the results of these sections is given at the beginning of Section 9.
This objection was made, by an anonymous referee, to an earlier version of this paper. I have quoted the objection, more or less verbatim, from the referee’s report.
For more on this, see Gillies (2004).
A Google search for causal models for the Framingham data produced only Korb et al (2004). Of course we may have missed some other papers, but there cannot be many of these.
References
Bandyoapdhyay, P. S., Nelson, D., Greenwood, M., Brittan, G., & Berwald, J. (2011). The logic of Simpson’s paradox. Synthese, 181, 185–208.
Campaner, R., & Galavotti, M.C. (2007). Plurality in causality. In P. Machamer & G. Wolters (eds.), Thinking about causes from Greek philosophy to modern physics. University of Pittsburgh Press, Ch. 10, pp. 178–199
Cartwright, N. (1979). Causal laws and effective strategies. Reprinted in How the laws of physics lie. Oxford: Oxford University Press, 1983, pp. 21–43.
Cartwright, N. (1989). Nature’s capacities and their measurement. Oxford: Oxford University Press.
Cartwright, N. (1995). False idealisation: a philosophical threat to scientific method. Philosophical Studies, 77, 339–352.
Cartwright, N. (2001). What is wrong with Bayes nets? The Monist, 84, 242–264.
Codell Carter, K. (2003). The rise of causal concepts of disease. Case Histories. Ashgate.
Doll, R., & Peto, R. (1976). Mortality in relation to smoking: 20 years’ observations on male British doctors. British Medical Journal, 2, 1525–1536.
Eells, E. (1991). Probabilistic causality. Cambridge: Cambridge University Press.
Galavotti, M. C. (2010). Probabilistic causality, observation and experimentation. In W. J. Gonzalez (Ed.), New methodological perspectives on observation and experimentation in science (pp. 139–155). A. Coruña: Netbiblo.
Gillies, D. (2004). An action-related theory of causality. The British Journal for the Philosophy of Science, 56, 823–842.
Gillies, D. (2011). The Russo-Williamson thesis and the question of whether smoking causes heart disease. In Illari, Russo, and Williamson, 2011, pp. 110–125.
Good, I.J. (1961). A causal calculus I. British Journal for the Philosophy of Science, 11, 305–318. Reprinted in I.J.Good, Good thinking. The foundations of probability and its applications. Minneapolis: University of Minnesota Press, pp. 197–217.
Good, I.J. (1962). A causal calculus II. British Journal for the Philosophy of Science, 12, 43–51. Reprinted in I.J.Good, Good thinking. The foundations of probability and its applications. Minneapolis: University of Minnesota Press, pp. 197–217.
Haavelmo, T. (1943). The statistical implications of a system of simultaneous equations, 11, pp. 1–12. Reprinted in D.F. Hendry & M.S. Morgan (eds.), The foundations of econometric analysis. Cambridge University Press, 1995, pp. 477–490.
Hennig, C. (2010). Mathematical models and reality – a constructivist view. Foundations of Science, 15, 29–48.
Hesslow, G. (1976). Discussion: two notes on the probabilistic approach to causality. Philosophy of Science, 43, 290–292.
Hitchcock, C. (2001). A tale of two effects. Philosophical Review, 110(3), 361–396.
Hitchcock, C. (2010). Probabilistic causality. Stanford encyclopedia of philosophy (http://plato.stanford.edu).
Illari, Phyllis, McKay, Russo, Federica, Williamson, J. (eds) (2011). Causality in the sciences. Oxford University Press.
Kim, J.H. & Pearl, J. (1983). A computational model for combined causal and diagnostic reasoning in inference systems. Proceedings of the 8 th International Joint Conference on AI (IJCAI-85), pp. 190–193.
Korb, K.B., Hope, L.R., Nicholson, A.E., Annick, K. (2004). Varieties of causal intervention. Pacific Rim International Conference on AI’04, pp. 322–331.
Lauritzen, S. L., & Spiegelhalter, D. J. (1988). Local computations with probabilities on graphical structures and their application to expert systems (with discussion). Journal of the Royal Statistical Society B, 50, 157–224.
Levy, D., & Brink, S. (2005). A change of heart. Unraveling the mysteries of cardiosvacular disease. New York: Vintage Books.
Neapolitan, R. E. (1990). Probabilistic reasoning in expert systems. Theory and algorithms. New York: John Wiley.
Pearl, J. (1982). Reverend Bayes on inference engines: a distributed hierarchical approach. Proceedings of the National conference on AI, ASSI-82, 133–136.
Pearl, J. (1985a). How to do with probabilities what people say you can’t. Proceedings of the Second IEEE Conference on AI Applications. Miami, Fl., pp. 6–12.
Pearl, J. (1985b). Bayesian networks: a model of self-activated memory for evidential reasoning. Proceedings of the Cognitive Science Society, Ablex, pp. 329–34.
Pearl, J. (1986). Fusion, propagation and structuring in belief networks. Artificial Intelligence, 29, 241–288.
Pearl, J. (1988). Probabilistic reasoning in intelligent systems. Networks of plausible inference. San Mateo, California: Morgan Kaufmann.
Pearl, J. (2000). Causality. models, reasoning, and inference. Cambridge: Cambridge University Press.
Pearl, J. (2011). The structural theory of causation. In Illari, Russo, and Williamson, 2011, pp. 697–727.
Popper, K. R. (1963). Conjectures and refutations. the growth of scientific knowledge. London: Routledge & Kegan Paul.
Reichenbach, H. (1956). In M. Reichenbach (Ed.), The direction of time. Berkeley: University of California Press. 1971.
Russo, F. (2009). Causality and causal modelling in the social sciences. New York: Springer.
Russo, F., & Williamson, J. (2007). Interpreting causality in the health sciences. International Studies in the Philosophy of Science, 21(2), 157–170.
Russo, F., & Williamson, J. (2011). Generic versus single-case causality: the case of autopsy. European Journal for Philosophy of Science, 1, 47–69.
Salmon, W. (1978). Why Ask, : “Why?”? An inquiry concerning scientific explanation. Reprinted in Salmon, 1998, pp. 125–141.
Salmon, W. (1980). Probabilistic causality. Reprinted in Salmon, 1998, pp. 208–232.
Salmon, W. (1998). Causality and explanation. Oxford: Oxford University Press.
Spirtes, P., Glymour, C., & Scheines, R. (1993). Causation, prediction and search. New York: Springer Verlag.
Sucar, L. E., Gillies, D. F., & Gillies, D. A. (1993). Objective probabilities in expert systems. Artificial Intelligence, 61, 187–203.
Suppes, P. (1970). A probabilistic theory of causality. Amsterdam: North-Holland.
Suppes, P. (1986). Non-Markovian causality in the social sciences with some theorems on transitivity. Synthese, 68(1), 129–140.
Twardy, C. R., & Korb, K. B. (2004). A criterion of probabilistic causality. Philosophy of Science, 71, 241–262.
Williamson, J. (2005). Bayesian nets and causality. Oxford: Oxford University Press.
Williamson, J. (2010). In defence of objective Bayesianism. Oxford: Oxford University Press.
Acknowledgments
Earlier drafts of this paper were read at the International Workshop on Causal Inference in the Health Sciences, which Maria Carla Galavotti and Raffaella Campaner organised in Bologna on 27-28 May 2011, and at a meeting of the Kent-UCL Causality group, held in UCL on 11 August 2011. Many comments were received at these meetings – some favourable, and some highly critical, indicating the controversial nature of the material. Later we received further comments, again some favourable and some highly critical, on subsequent drafts of the paper. We have tried to take into account both types of comment in revising the paper, and would like to thank those who made comments, particularly Carlo Berzuini, Raffaella Campaner, Nancy Cartwright, Brendan Clarke, David Corfield, Philip Dawid, Maria Carla Galavotti, Phyllis McKay Illari, Judea Pearl, Federica Russo, Jon Williamson, and several anonymous referees.
Author information
Authors and Affiliations
Corresponding author
Additional information
Although the two authors collaborated on all aspects of the paper, the philosophical parts were mainly the work of Donald Gillies, and the mathematical parts of Aidan Sudbury. In particular the proofs of Theorems 1 and 2 were due to Aidan Sudbury. Both authors would like to acknowledge the very important contribution to the paper of Christian Hennig. In early discussions, it was Christian Hennig who made the key points which led to the mathematical formulation of the problem in Section 6, and he also made the interesting comment on the conditions of Theorem 1, which we have included as Section 8. However, Christian Hennig’s philosophy of probability and statistics is rather different from the one presupposed in this paper. A general view of his philosophy is to be found in Hennig (2010), and he is at the moment developing it in more detail.
Appendices
Appendix
Definitions of Terms Used
A network or net is a directed acyclic graph.
The nodes or vertices of a network are variables, which are denoted by capital letters, e.g. X, Y, Z, A, B, ….
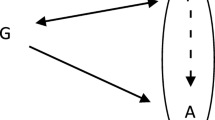
If an arrow joins two nodes of a network A, B (see Fig. 11), then A is said to be a parent of B, and B is said to be a child of A. Children, children of children, etc. of A are said to be descendants of A.
If an arrow joining any two nodes A, B (see Fig. 11) of a network means that A has a causal influence on B, then the network is said to be a causal network.
If the set of variables of a network, X1, X 2, …, Xn say, are random variables all defined on some underlying probability space and so having a joint distribution, then the network is said to be a probability network.
The Markov Condition is satisfied for a node A of a network, if A, conditional on its parents, is probabilistically independent of any other set of nodes in the network not containing any of A’s descendants.
A probability network in which every node satisfies the Markov condition is said to be a Bayesian network.
In a Bayesian network, the parents of a node are said to screen it off from the other nodes of the network except its descendants.
If a causal network is also a probability network, it is said to be a causal probability network, or causal model. When the term ‘causal network’ is used in this paper with no further qualification, it will be assumed to be a causal probability network.
Note that when Pearl introduced the term Bayesian network or Bayes network in his 1985b, he used it to refer to causal Bayesian networks. In fact Pearl wrote (1985b, p. 330):
“Bayes networks are directed acyclic graphs in which the nodes represent propositions (or variables), the arcs signify the existence of direct causal influences between the linked propositions, and the strengths of these influences are quantified by conditional probabilities.”
We here, following a later convention, defined Bayesian networks purely probabilistically, so that the arrows in a Bayesian network need not represent causal influences. However, when the term ‘Bayesian network’ is used in this paper with no further qualification, it will be assumed to be a causal Bayesian network.
A causal model, in which every node satisfies the Markov condition, is said to be a Markovian causal model.
A causal model, in which at least one node does not satisfy the Markov condition, is said to be a non-Markovian causal model.
Rights and permissions
About this article
Cite this article
Gillies, D., Sudbury, A. Should causal models always be Markovian? The case of multi-causal forks in medicine. Euro Jnl Phil Sci 3, 275–308 (2013). https://doi.org/10.1007/s13194-013-0068-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13194-013-0068-z