Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T06:31:58.738Z Has data issue: false hasContentIssue false
  • English
  • Français

Finitely constrained classes of homogeneous directed graphs

Published online by Cambridge University Press:  12 March 2014

Brenda J. Latka
Brenda J. Latka*
Affiliation:
Department of Mathematics, Lafayette College, Easton, Pennsylvania18042-1781, E-mail: latka@lafvax.lafayette.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a finite relational language L is there an algorithm that, given two finite sets 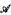and 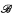of structures in the language, determines how many homogeneous L structures there are omitting every structure in 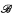and embedding every structure in ?

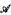For directed graphs this question reduces to: Is there an algorithm that, given a finite set of tournaments Γ, determines whether 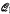Γ, the class of finite tournaments omitting every tournament in Γ. is well-quasi-order?

First, we give a nonconstructive proof of the existence of an algorithm for the case in which Γ consists of one tournament. Then we determine explicitly the set of tournaments each of which does not have an antichain omitting it. Two antichains are exhibited and a summary is given of two structure theorems which allow the application of Kruskal's Tree Theorem. Detailed proofs of these structure theorems will be given elsewhere.

The case in which Γ consists of two tournaments is also discussed.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 1 , March 1994 , pp. 124 - 139
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bollobás, Belá, Combinatorics, Cambridge University Press, Cambridge, 1986.Google Scholar
[2]Cameron, Peter, Orbits of permutation groups on unordered sets I, Journal of the London Mathematical Society, vol. 17 (1978), pp. 410–414.CrossRefGoogle Scholar
[3]Cherlin, Gregory, Homogeneous directed graphs II, graphs embedding I∞, submitted.Google Scholar
[4]Cherlin, Gregory, Homogeneous directed graphs II, graphs omitting I∞, submitted.Google Scholar
[5]Cherlin, Gregory, Homogeneous directed graphs I, the imprimitive case, Logic Colloquium 1985, North-Holland, Amsterdam, 1987, pp. 67–88.Google Scholar
[6]Cherlin, Gregory, Homogeneous tournaments revisited, Geometria Dedkatae, vol. 256 (1988), pp. 231–240.Google Scholar
[7]Cherlin, Gregory, Combinatorial problems connected with finite homogenity, Contemporary Mathematics, vol. 131, part 3, American Mathematical Society, Providence, RI, 1992, pp. 3–30.Google Scholar
[8]Fraissé, Roland, Sur l'extension aux relations de quelques properietés des ordres, Annates Scientifiques de l'École Normale Superiéure, vol. 71, (1954), pp. 361–388.Google Scholar
[9]Henson, C. Ward, Countable homogeneous relational systems and categorical theories, this Journal, vol. 37 (1972), pp. 494–500.Google Scholar
[10]Higman, Graham, Ordering by divisibility in abstract algebras, Proceedings of the London Mathematical Society, vol. 2, (1952), pp. 326–336.CrossRefGoogle Scholar
[11]Kruskal, J. B., Well-quasi-ordering, the tree theorem, and Vazsonyi's conjecture, Transactions of the American Mathematical Society, vol. 95, (1960), pp. 210–225.Google Scholar
[12]Lachlan, Alistair H., Countable homogeneous tournaments, Transactions of the American Mathematical Society, vol. 284, (1984), pp. 431–461.CrossRefGoogle Scholar
[13]Lachlan, Alistair H., On countable stable structures which are homogeneous for a finite relational language, Israel Journal of Mathematics, vol. 49 (1984), pp. 69–153.CrossRefGoogle Scholar
[14]Nash-Williams, C. St. J. A., On well-quasi-ordering finite trees, Proceedings of the Cambridge Philosophical Society, vol. 59, (1963), pp. 833–835.CrossRefGoogle Scholar