For any linear order type τ with first element let 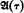be the Boolean set algebra generated by the left-closed right-open (including [x, ∞)) intervals of some linear order of type τ. Let η and ω be the order types of the rationals and natural numbers respectively (when not used as an order type, ω will, as usual, be the set of nonnegative integers). We show that the Boolean algebra of the elementary theory of well-orders, i.e., the Boolean algebra of elementary classes of well-orders or, equivalently, the algebra of equivalence classes of sentences of the elementary theory of well-orders, is isomorphic to 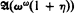and that the Boolean algebra of the elementary theory of abelian groups is isomorphic to 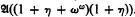. Both results are obtained by applying Hanf's structure diagram technique to the work of Mostowski, Tarski, and Szmielew. One may formalize discussion of algebras of proper classes by assuming the classes are included in a universe which is a set in a larger universe. Given a Boolean algebra, let 0 be its zero and 1 its unit, let ≤ be its associated partial ordering, and, for any elements a, b, and c of the algebra, let “a + b = c ” be the assertion that c is the disjoint sum of a and b. A subset of the algebra disjointly generates the algebra iff each of the algebra's elements is a disjoint sum of a finite number of the subset's elements.