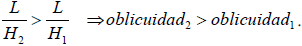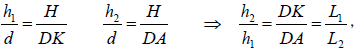Resúmenes

ARTIGOS

La tensión entre estática y dinámica desde la Antigüedad hasta el Renacimiento

Daniel Silvio Vaccaro

Profesor de la Facultad de Ingeniería, Universidad Austral, Buenos Aires, Argentina. DVaccaro@austral.edu.ar

RESUMEN

Que la estática es un capítulo más de la física es aceptado con total naturalidad desde que Newton estableció las bases de la mecánica clásica. Pero estas dos disciplinas, estática y dinámica, tienen historias diferentes, con encuentros y desencuentros, desde la Antigüedad hasta el Renacimiento. En este artículo, se describe parte de este proceso en relación a algunos aspectos de la mecánica, en particular de la estática. Cómo esta disciplina quedó establecida, ya en la Antigüedad, en forma rigurosa y matemática, mientras que la dinámica se enfrentó con dificultades conceptuales y empíricas que comenzaron a esclarecerse recién en el Renacimiento. Las leyes de la estática fueron establecidas inicialmente por Arquímedes utilizando un sistema axiomático riguroso. En el presente artículo, se muestra cómo la tradición arquimediana resurgió con gran impulso durante el renacimiento mientras existía la tradición rival de aquellos que estaban dispuestos a sacrificar hasta cierto punto el rigor matemático, recurriendo a principios dinámicos de fundamentación dudosa pero de eficacia heurística. Galileo fue un exponente claro de la nueva cultura renacentista y no renunció a conectar las tradiciones estática y dinámica, pero a la vez consideraba posible fundamentar rigurosa y geométricamente el estudio del movimiento, y fue quien logró resolver la crisis entre estática y dinámica, conduciendo la matemática renacentista a una realización exitosa y contribuyendo al nacimiento de una nueva física.

Palabras-clave: Arquímedes. Física aristotélica. Galileo. Estática. Dinámica. Antigüedad. Renacimiento. Momento. Palanca. Plano inclinado.

ABSTRACT

Since Newton established the bases of classical mechanics, it has been readily accepted that statics is a chapter of physics. However, from Antiquity to the Renaissance the two disciplines, statics and dynamics, had different histories that only sometimes interacted with one another. In this article, part of this process is described whereby statics was established during Antiquity in rigorous and mathematical form, whereas dynamics confronted conceptual and empirical difficulties, which began to be clarified only in the Renaissance. The laws of statics were initially established by Archimedes using a rigorous axiomatic system. It is shown that while there was a strong resurgence of the Archimedean tradition during the Renaissance, there was also a rival tradition that was, up to a point, disposed to sacrifice mathematical rigor, and instead make use of dynamical principles that have dubious foundation but that are heuristically efficacious. Galileo was a clear exponent of the new Renaissance culture interested in connecting the traditions of statics and dynamics; he considered it possible to give a rigorous and geometrical foundation to the study of movement, that enabled him to resolve the tension between statics and dynamics and to bring Renaissance mathematics to a successful realization that contributed to the birth of a new physics.

Keywords: Archimedes. Aristotelian physics. Galileo. Statics. Dynamics. Antiquity. Renaissance. Momentum. Lever. Inclined plane.

Introducción

Las leyes que rigen el equilibrio mecánico de los cuerpos se obtienen como un caso particular de las leyes generales de la dinámica newtoniana con la sola condición de hacer que todas las aceleraciones valgan cero. Por lo tanto, que la estática es un capítulo más de la física es aceptado con total naturalidad desde que Newton estableció las bases de la mecánica clásica.

Pero estas dos disciplinas, estática y dinámica, tienen historias diferentes, con encuentros y desencuentros, hasta el Renacimiento. Aristóteles, en su física, consideró al movimiento como el concepto central "ya que la naturaleza es un principio de movimiento y de cambio (...) no podemos dejar de investigar qué es el movimiento" (Física, III, 1, 200b1-3). El concepto de movimiento para Aristóteles es mucho más amplio que el de desplazamiento o cambio de lugar. Además dicho concepto está fuertemente comprometido con las concepciones metafísicas y cosmológicas de su filosofía. Aristóteles y los aristotélicos en la Antigüedad, en la Edad Media y en el Renacimiento se ocuparon en particular del movimiento local como un aspecto particular de la física. Esa ciencia del movimiento local presentaba ciertos conflictos con la observación, mientras que la estática parecía ajustarse perfectamente a ella.

En la física aristotélica, ocupa un lugar central la causa final que sería la respuesta a la pregunta: ¿Hacia dónde se dirige espontáneamente la naturaleza para producir el orden y la perfección que la caracterizan? Entonces para Aristóteles el movimiento natural es un proceso teleológico. En particular, el movimiento natural local no es un estado de las cosas ante el cual éstas se muestran indiferentes, sino un proceso que conduce a actualizar el lugar propio que corresponde a cada cuerpo en el cosmos ordenado espacialmente.

La estática, dentro de las ciencias griegas de la Antigüedad, estaría ubicada dentro de las ciencias matemáticas aplicadas, también llamadas "ciencias mixtas". El objeto de tal disciplina es el estado de equilibrio mecánico de los cuerpos. Las leyes de la estática fueron establecidas inicialmente por Arquímedes utilizando una geometrización de los fenómenos y formuladas en un sistema axiomático riguroso. El rigor del enfoque de Arquímedes se logró a costa de restringir el tipo de problemas tratados y los conceptos básicos empleados (cf. Solís & Sellés, 2005).

Entre Aristóteles y Arquímedes está el texto Problemas mecánicos. Esta obra está incluida en el corpus aristotélico ya que durante mucho tiempo se creyó que el autor era el propio Aristóteles. Se supone que se escribió después de la muerte del estagirita y antes del nacimiento de Arquímedes y que el autor pudo haber sido un discípulo de aquel. En dicha obra del siglo III a.C. encontramos planteados, como su nombre lo indica, un conjunto de problemas o preguntas referidas a cuestiones relativas a las máquinas simples. Desde entonces se inició un camino que con el correr de los siglos llevaría a reajustar la relación entre matemática y física, para lo que contribuyo, en particular en la estática, los diversos intentos de deducir las leyes de la estática a partir de principios dinámicos basados en la física aristotélica.

1 La física aristotélica

La física de Aristóteles es el estudio de la naturaleza y ésta es el conjunto de sustancias naturales. Aristóteles (384-322 a.C.) denomina sustancia a todo aquello que puede existir por sí mismo, y accidente a todo aquello que requiere de otro para existir. Pero como la ciencia debe tratar de encontrar la esencia universal que se encuentra en cada una de las sustancias naturales, Aristóteles concibe a toda sustancia como un compuesto de un sustrato material (hyle) y un componente universal, que es su esencia o forma (morphé). A esta concepción se la denomina hilemorfismo.

Aristóteles fue un distinguido naturalista comprometido filosóficamente con la plena realidad de los individuos mutables que constituyen el mundo sensible y, por lo tanto, el punto de partida de su filosofía natural fue asumir el punto de vista de sentido común de que el cambio es auténtico (cf. Lindberg, 2002). En palabras del propio Aristóteles:

Un acto de movimiento o cambio exige un agente y un paciente y ambos deben ser compatibles. El paciente no puede responder al influjo del agente a no ser que posea la facultad de actuar así. Ésta es su dynamis. Una piedra sujeta al mismo influjo que una semilla no se desarrollará en una planta.

Al impugnar la existencia de entidades universales en un mundo separado, pero admitir al mismo tiempo que toda ciencia (episteme) es de lo universal, uno de los principales problemas de la metafísica de Aristóteles es cómo concebir tales universales como objetos de la ciencia. El universal no es un concepto subjetivo ni un modo de expresión. Si lo consideramos en el objeto, es su esencia (lo que le hace ser lo que es). Si lo consideramos en la mente, es la definición (concepto) universal de tal esencia. El universal no existe en ningún estado de separación fuera de la mente. Es real tanto en la mente como en el objeto, aunque su existencia en la cosa no implica la universalidad formal que tiene en la mente.

Examinando las doctrinas de los filósofos precedentes sobre lo que hace que algo sea lo que es, Aristóteles dirá que algunos han enfatizado la causa material, otros la causa formal, otros la causa eficiente. Reconocerá que efectivamente todas estas son causas verdaderas, la material se refiere a aquello de lo que algo está hecho, la formal a aquello a lo que algo llega a ser y la eficiente la que origina el movimiento. Sin embargo, Aristóteles considerará que esta lista es incompleta. Es necesaria una causa que cumpla el papel rector que cumplía la idea de bien en la filosofía platónica: postula una cuarta causa, la causa final. La causa final es el fin al que se dirigen todas las cosas y que también forma parte de la explicación del por qué algo es como es, o cambia del modo en que lo hace. La causa final es igual a la causa formal en potencia que llega a ser forma en acto gracias a la causa agente. Con ello Aristóteles inaugura las explicaciones teleológicas, explicaciones a través de su fin (telos). Este tipo de explicaciones le permitirá una concepción global del cambio natural (concepción organicista), como actualización de la forma hacia su punto máximo de perfección. Solís & Sellés (2005) se refieren a estos temas de la siguiente manera:

Para Aristóteles, todas las sustancias se consideran compuestos de los cuatro elementos simples: tierra, agua, aire y fuego y cada uno de éstos, a su vez, como una combinación de los cuatro principios opuestos primarios: lo seco, lo húmedo, lo frío y lo caliente (cf. Lloyd, 1977). La física de Aristóteles se concibe como una explicación de las cualidades sensibles. Su forma misma de plantear la cuestión lo remite a una teoría cualitativa. Sugerir que estas cualidades derivan a su vez de diferencias cuantitativas más fundamentales sería, según su punto de vista, dar una respuesta equivocada al problema; en realidad, confundir su misma naturaleza (cf. Lloyd, 1977). El movimiento natural de estos cuatro elementos terrestres desde el centro de la Tierra es tanto hacia arriba como hacia abajo; el agua y la tierra, naturalmente, caen. Por supuesto que también pueden moverse en otras direcciones pero el movimiento de una piedra arrojada no es natural sino violento porque requiere de un agente impulsor. El movimiento de una llama al elevarse es un movimiento natural. Pero el movimiento circular de los cuerpos celestes, por ser eterno no puede ser forzado, por consiguiente debe ser natural. Por otro lado, un objeto que se mueve naturalmente en círculos no puede estar formado por elementos terrestres. Por lo tanto, para Aristóteles, los cuerpos celestes están formados por una sustancia muy diferente, un quinto elemento, aither (cf. Lloyd, 1977). La física de Aristóteles es cualitativa para que se pueda aplicar la lógica deductiva. Es decir a partir de premisas físicas y a través del silogismo se alcanzan conclusiones físicas.

Según Lloyd (1977), no es exagerado afirmar que antes de Aristóteles no existía en la ciencia griega nada digno de ser llamado dinámica. Los textos de Aristóteles suministran las primeras enunciaciones generales concernientes a las relaciones entre los diversos factores que rigen la velocidad de un cuerpo en movimiento. Así como su cosmología es doble, también hay dos dinámicas: la de los objetos terrestres, o más generalmente, de la región sublunar, y la de los objetos celestes. Para cada elemento terrestre en estado puro existe un lugar natural. El más pesado, la tierra, se ubicará en el centro del universo. El agua sobre la tierra. El aire sobre el agua y el lugar del fuego es la región entre el aire y la esfera de la luna, la esfera inferior de la región celeste.

2 Las ciencias matemáticas griegas

En la tradición científica occidental, ha habido un largo debate sobre la aplicabilidad de las matemáticas a la naturaleza. La cuestión es si el mundo es fundamentalmente matemático, en cuyo caso el análisis matemático es el camino más seguro para una comprensión más profunda, o si las matemáticas son aplicables sólo a los aspectos superficiales cuantificables de las cosas, sin alcanzar realidades últimas (cf. Lindberg, 2002). Es bastante obvio que para las ciencias naturales desde el Renacimiento hasta nuestros días ha habido un progresivo énfasis en el enfoque matemático. Sin embargo el debate entre ambas posiciones sigue vigente entre los científicos sociales y los historiadores.

En la antigüedad, la posición de predominio de la matemática fue asumida por los pitagóricos, y posteriormente fue tomada muy en serio por Platón. Pero para Aristóteles, de quien no nos cabe duda que poseía formación matemática por haber sido miembro de la Academia de Platón, existía una diferencia entre las matemáticas y la ciencia natural o física. "La física, por definición, considera las cosas naturales en su totalidad, como cuerpos sensibles, mutables. El matemático, en cambio, desnuda los cuerpos de todas las cualidades sensibles y se concentra en las matemáticas restantes" (Lindberg, 2002, p. 122). Aristóteles en su Física se ocupa específicamente de este tema:

Contra los pitagóricos y platónicos, para Aristóteles, las entidades matemáticas sólo son formas abstraídas de un sujeto material y, como tales, no tienen una existencia realmente independiente. Cuando la física considera los atributos geométricos los toma como accidentes, mientras que las matemáticas los estudian por sí mismos, haciendo abstracción de los cuerpos físicos a que pertenecen.

En el siglo IV a.C., las conquistas de Alejandro Magno pusieron a los griegos en contacto con las matemáticas de los pueblos orientales. En Alejandría, se fundó el Museo, con su famosa biblioteca, en el que los eruditos se dedicaban al estudio de diversas disciplinas. Entre ellas, a las matemáticas, que incluían los campos más abstractos de la geometría, la aritmética y el álgebra. Pero las investigaciones se ocupaban

Por lo tanto, la estática es una de estas ciencias "medias" o "mixtas" en donde los términos mayores y menores de los silogismos científicos son de tipo físico y el término medio es matemático. Uno de los temas centrales de la estática es el equilibrio de la balanza tanto la de brazos iguales como la de brazos desiguales conocida como balanza romana. Pero este tema puede incluirse a su vez en uno mucho más general: la palanca. En la ciencia de la palanca, la física parecía casi completamente reducible a lo matemático (cf. Linberg, 2002). El desarrollo, en la Antigüedad, de la ciencia de la estática está íntimamente vinculado con la mecánica o ciencia de las máquinas. Desde el siglo IV a.C., la mecanización avanzó en sectores estratégicos como en la minería, en la ingeniería militar y en la navegación, especialmente en Siracusa (Arquímedes, siglo III a.C.), en Alejandría (Herón, siglo I d.C.) y en Bizancio (Filón, siglo III a.C.).

Un importante testimonio acerca de esta época de gran desarrollo técnico y científico es la Colección matemática de Pappo de Alejandría (ca. 300 d.C.). Este gran matemático griego de la escuela alejandrina escribió comentarios a los Elementos de Euclides y a la gran sintaxis matemática de Tolomeo, llamada Almagesto por los árabes. Su obra principal, la Colección matemática, escrita hacia el 340, reviste una particular importancia desde el punto de vista histórico, porque, además de ser una exposición completa y sistemática de los conocimientos de su época, recoge fragmentos, a veces íntegros, de las obras que constituían los fundamentos de la enseñanza de las matemáticas en la ciudad de Alejandría, hoy en gran parte perdidas. La Colección está compuesta por ocho libros, casi todos conservados. El libro VIII trata sobre la ciencia de la mecánica que para Pappo no es solamente útil por sus muchas e importantes aplicaciones prácticas de interés para los hombres, sino que es estimada por los filósofos y matemáticos, ya que fundamentalmente concierne a la doctrina de la naturaleza con especial referencia a la composición material del cosmos. Según Pappo, ya que la mecánica estudia la estabilidad de los cuerpos tanto como su tendencia natural a caer y sus movimientos en general, no sólo establece las causas de su movimiento natural, sino que permite diseñar dispositivos por medio de los cuales es posible impulsar a los cuerpos a cambiar su posición, oponiéndose a sus naturalezas (tendencias naturales), en una dirección más allá de sus lugares naturales (cf. Lahanas, 2006; Cohen & Drabkin, 1958).

3 Los Problemas mecánicos de la tradición aristotélica (pseudo-Aristóteles)

Uno de los primeros textos que se conservan, y a la vez muy significativo, sobre esta relación entre estática y dinámica son los Problemas mecánicos. Esta obra es un producto de la escuela peripatética posterior a Aristóteles, pero, como la tradición se la atribuyó a Aristóteles y no se conoce su verdadero autor, se la llama pseudo-Aristóteles. Solís y Sellés consideran que su posible autor haya sido Estratón, que murió en el 268 a.C., y que fuera el tercer director del Liceo. Según estos autores:

El contraste entre estos dos enfoques se puede apreciar si se compara a Arquímedes con Estratón, el tercer director del Liceo y posible autor de los Problemas mecánicos. Desde la perspectiva de la mecánica, Estratón consideraba que las diversas tendencias al movimiento de los elementos de Aristóteles se reducían a una sola: el peso. Consideraba que la ligereza no era la tendencia natural de moverse hacia arriba si no el resultado del desplazamiento hacia arriba de lo menos pesado provocado por el descenso de lo más pesado.

Los Problemas mecánicos constituyen una colección de 35 problemas, unos sobre máquinas y otros sobre cuerpos en movimiento. La idea básica de este tratado es que casi todos los movimientos se reducen al caso de la palanca, que remite al uso de la balanza y a la vez a las propiedades de la circunferencia (cf. Solís & Sellés, 2005). Esta obra, de gran influencia en el Renacimiento, comienza así:

3.1 ¿Por qué pequeñas fuerzas pueden mover grandes pesos con una palanca?

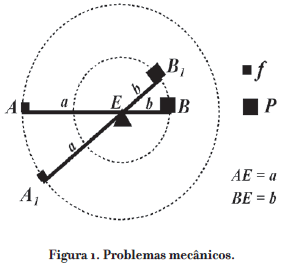
Así está planteado el Problema 3 de los Problemas mecánicos. El autor nos explica que la palanca es una barra AB con un fulcro E (punto de apoyo) que la divide en partes de distinta longitud EA > EB como podemos apreciar en la figura 1. Dicho punto de apoyo es un centro, es decir, no se mueve. Sobre los extremos de la barra hay dos pesos:

El autor enuncia la ley de la palanca: la razón entre el peso movido P al peso que causa el movimiento f es igual a la razón inversa de las distancias desde el centro. En lenguaje moderno lo expresamos así:

P/f = a/b o Pb = fa.

Cuando la fuerza f se desplaza desde A hasta A1 describe un arco de circunferencia AA1 mayor que el desplazamiento del peso P según el arco BB1. De esta manera, una fuerza provoca mayor movimiento al actuar a una distancia mayor del fulcro (cf. Winter, 2007; Aristóteles, 1936). Se podría decir que, en esta obra, encontramos un antecedente de la definición de momento de una fuerza.

Acabamos de exponer una de las primeras explicaciones que han sobrevivido del funcionamiento de la palanca. Es importante hacer notar que es una explicación "dinámica" de un fenómeno "estático", ya que la ley enunciada anteriormente es válida para el caso en que la palanca se mantenga en equilibrio. Podemos inferir que el autor quiere decir que, si la palanca se pusiera en movimiento, las velocidades de los pesos serían inversamente proporcionales a la magnitud de dichos pesos (cf. Lindberg, 2002), aunque esto no se enuncia explícitamente (cf. Solís & Sellés, 2005).

Según Solís y Sellés (2005), en Problemas mecánicos, se pone a la par el mundo natural y el mundo artificial. A partir de entonces, los ingenieros alejandrinos iniciaron el estudio teórico y sistemático de las máquinas. Es decir que, en el siglo III a.C., filósofos y matemáticos se ocuparon del sorprendente mundo de las máquinas, iniciando un largo camino que llevaría con el tiempo a reajustar la relación entre física y matemática. El estudio de las máquinas simples como la palanca, la polea, engranajes, plano inclinado y de las combinaciones entre ellas presenta una relativa simplicidad a la vez que una gran posibilidad de control. Estas investigaciones permitieron el aislamiento de los elementos esenciales del funcionamiento de las máquinas y facilitaron la formulación de conceptos y principios con que sistematizar deductivamente las leyes de operación. Sin embargo, la relación entre geometría, máquinas y experimentación siguió un camino tortuoso hasta alcanzar el éxito con el mecanicismo del siglo XVII.

4 Arquímedes y la ley de la palanca

Arquímedes (ca. 287-211 a.C.) contribuyó tanto a la matemática teórica como a la aplicada y es estimado especialmente por la elegancia de sus demostraciones matemáticas. En particular, nos ocuparemos en esta sección de su demostración estática de la ley de la palanca tal como fue desarrollada en Sobre el equilibrio de los planos. En ella, Arquímedes elimina la consideración dinámica del movimiento para centrarse en los casos de equilibrio estático y hace abstracción de consideraciones físicas de los cuerpos, tales como naturalezas y tendencias teleológicas (cf. Solís & Sellés, 2005). Si exceptuamos la afirmación de que los pesos efectivamente pesan, las consideraciones físicas no aparecen por ningún lado. El brazo de la palanca es considerado como una línea inmaterial y los pesos se aplican a puntos geométricos (cf. Lindberg, 2002). La demostración tiene el estilo de Euclides a partir de premisas que se establecen por intuición y simetría geométrica. Los postulados de Sobre el equilibrio de los planos son los siguientes (Cohen & Drabkin, 1958, p. 186-8):

Se sobreentiende que las distancias se miden desde el fulcro o punto de apoyo de la palanca.

En los postulados 2 y 3, se considera de manera implícita que todo es pesado y que la ligereza de un cuerpo no es otra cosa que la cualidad de ser menos pesado que otro cuerpo. Por otra parte, estos postulados resultan evidentes si nos imaginamos en la situación de estar realizando pesadas en una balanza de platillos de brazos iguales.

Este postulado establece que figuras semejantes, es decir de la misma "forma", pero desiguales, es decir de diferente tamaño, tendrán sus centros de gravedad en la misma posición "relativa".

En este postulado, se plantea que a los efectos del equilibrio sólo son relevantes la magnitud y la distancia, con independencia de la forma o la sustancia. Es fundamental para la deducción de la ley de la palanca. Cuando Arquímedes dice "magnitudes iguales a otras magnitudes", quiere decir "magnitudes del mismo peso". Y cuando dice "magnitudes a ciertas distancias" quiere decir "los centros de gravedad de las magnitudes están a la misma distancia del fulcro" (Assis, 2008, p. 179).

Con estos postulados, Arquímedes ha convertido un ámbito físico en una cuestión geométrica y, en el libro I de Sobre el equilibrio de los planos, procede a demostrar rigurosamente siete proposiciones sobre el equilibrio.

Enuncia la inversa de la primera parte del Postulado 1, que se puede demostrar por el absurdo utilizando el Postulado 3. De acuerdo al Postulado 1 y a la Proposición 1, la igualdad de pesos y distancias es condición necesaria y suficiente del equilibrio.

Es interesante visualizar gráficamente lo expresado en el corolario 2, ya que es esencial en la demostración de la ley de la palanca. Los cuerpos indicados con letras mayúsculas iguales, en la figura 2, tienen pesos iguales. Dichos cuerpos están situados en posiciones simétricas respecto del eje de simetría que pasa por el punto medio ubicado entre los dos cuerpos centrales. Dicho eje de simetría perpendicular a la línea que une todos los centros de gravedad de los n cuerpos determina el centro de gravedad del sistema.

4.1 Demostración de la ley de la palanca

La ley de la palanca fue demostrada por Arquímedes como la Proposición 6 de Sobre el equilibrio de los planos, para el caso en que el cociente entre el peso mayor y el peso menor es un número entero:¹ 1 En la proposición 7, Arquímedes completa la demostración para el caso de magnitudes inconmensurables.

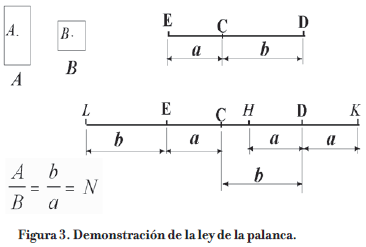
Observemos la figura 3 y supongamos que las magnitudes (pesos) A y B son conmensurables y que los puntos A y B son sus centros de gravedad. Sea DE un línea recta dividida en el punto C en dos segmentos: EC de longitud a y CD de longitud b. Supongamos que estas longitudes verifican la relación: A/B = b/a. Tenemos que probar que si A se ubica en E y B se ubica en D, C es el centro de gravedad común de ambos tomados conjuntamente.

Como los pesos A y B son conmensurables, también lo serán b y a. Sea N una medida común de ambos. Tracemos HD y DK ambas iguales a EC, es decir, de longitud a. Tracemos LE igual a CD, es decir, de longitud b. Entonces EH = CD, ya que HD = EC. Como se puede apreciar en la figura 3,

EH= a + CH y CD= b = a + CH.

Por lo tanto, el segmento LH está dividido en dos partes iguales, de longitud b, por el punto E y el segmento HK está dividido en dos partes iguales, de longitud a, en el punto D. Tomemos una magnitud (peso) Z que esté contenida en el peso A, tantas veces como N está contenida en LH. De esto concluimos que: A/Z = LH/N. Pero como , entonces . Por lo tanto, Por lo tanto, el peso Z está contenido un número entero de veces tanto en el peso A como en el peso B.

Si dividimos tanto el segmento LH como el segmento HK en partes de igual longitud N y dividimos los pesos A y B en partes iguales a Z, como se muestra en la figura 4, la cantidad de partes en que quedará dividido el peso A será igual a la cantidad de partes en que quedará dividido el segmento LH. De igual modo, el peso B quedará dividido en una cantidad de partes iguales a Z y dicha cantidad será igual a la cantidad de partes en que quedará dividido el segmento HK.

De esta manera, hemos distribuido el peso A a lo largo del segmento LH en forma simétrica respecto del punto E. El Corolario 2 de la Proposición 5 nos permite afirmar que E es el centro de gravedad de A. En forma análoga, el peso B ha quedado repartido en partes iguales a lo largo del segmento HK, cuyo punto medio es D. Por lo tanto, D es el centro de gravedad del peso B.

Como C es el punto medio de LK, entonces C es el centro de gravedad de los pesos A y B tomados en forma conjunta. Por lo tanto, A actuando en E y B actuando en D estarán en equilibrio respecto al punto C (cf. Solís & Sellés, 2005, p. 151-2; Cohen & Drabkin, 1958, p. 186-9).

4.2 La idea clave de la prueba

Consideremos una barra sin peso de la cual cuelgan 6 unidades equidistantes de igual peso. La barra está suspendida de su punto medio C y, por lo tanto, en equilibrio. Las 6 unidades están suspendidas de los puntos medios de 6 segmentos iguales en que ha sido dividida la barra (cf. Renn; Damerow & McLaughlin, 2003). Esta situación se ilustra en la figura 5.

Estas 6 unidades de peso están repartidas de la siguiente manera: 4 unidades forman el cuerpo A (cuadros oscuros) y 2 unidades forman el cuerpo B (cuadros en color claro). Estas seis unidades están situadas en el punto medio de cada una de las seis secciones iguales en que se ha dividido la barra. A continuación el cuerpo A (cuadros oscuros) se cuelga de una barra adicional que a su vez cuelga de la primera barra, pero la posición relativa de estas 4 unidades de peso no cambia. Hacemos lo mismo con las 2 unidades que forman el cuerpo B. El equilibrio se mantiene, si las barras adicionales están suspendidas de sus respectivos puntos medios E y D.

El tercer paso en la deducción de Arquímedes consiste en considerar que el equilibrio no se modificará, si todo el cuerpo A se suspende del punto E y todo el cuerpo B se suspende del punto D (cf. Assis, 2008). Llegamos al caso particular en que un cuerpo de 4 unidades de peso ubicado a una distancia de 1 unidad del punto de suspensión C está equilibrado por un cuerpo de 2 unidades de peso ubicado a una distancia de 2 unidades. Como podemos apreciar, este resultado, ilustrado en la figura 6, es fácilmente generalizable. En este sencillo análisis, podemos reconocer cómo el Postulado 6 ("si magnitudes a ciertas distancias están en equilibrio, otras magnitudes iguales a ellas también estarán en equilibrio a las mismas distancias") es la premisa fundamental que le permite a Arquímedes demostrar la ley de la palanca. Concluimos este análisis acordando con Lindberg que:

4.3 La crítica de Mach a la demostración de Arquímedes

El físico Ernest Mach (1838-1916), en su análisis histórico-crítico de la mecánica, expuso una crítica a la demostración de Arquímedes. Según Mach, la demostración contiene presupuestos que no se explicitan y que se deben obtener de la experiencia. A pesar de la elegancia y el rigor lógico de la demostración, Mach se cuestiona:

Lo que nos quiere decir Mach es que si la dependencia del momento con D no fuera lineal, no serían válidas las transformaciones que hemos visto en los gráficos de la sección anterior. Por ejemplo, 4 unidades de peso actuando en E no serían equivalentes a esas mismas 4 unidades actuando en forma "distribuida". Es decir, la dependencia lineal P×D ya está supuesta desde el inicio en la demostración.

Otros historiadores, como Valiati y Hölder, se han opuesto a la crítica de Mach. En forma análoga, lo ha hecho Dijksterhuis enfatizando que en el paso crítico de su prueba, Arquímedes hace uso del concepto de centro de gravedad (cf. Renn; Damerow & McLaughlin, 2003).

En efecto, en las figuras 5 y 6 que hemos utilizado para ilustrar la sección 4.2, podemos apreciar que el centro de gravedad del cuerpo de peso A (4 unidades) está en E y el centro de gravedad del cuerpo de peso B (2 unidades) está en D. Del mismo modo, la distribución inicial tiene su centro de gravedad en C en forma independiente del tipo de función que vincula momento con distancia siempre que se respete la simetría; lo que se aceptaría como evidente (cf. Assis, 2008).

En la figura 7, designamos con P1, P2...P6 al peso de cada uno de los 6 cuerpos colgados de la barra, y con L a la longitud total de la barra LK. Si utilizamos la definición correcta de momento estático y nos basamos en la figura 7, el equilibrio queda determinado por la igualdad:

Podemos apreciar que el equilibrio se verifica, si P1 = P2, P3= P4 y P5 = P6, una condición más restrictiva que la utilizada en la demostración donde todos los cuerpos tienen igual peso. Además, si la dependencia del momento con la distancia no fuera lineal, siempre que se mantenga la condición de simetría, el equilibrio respecto de C se conserva. Dicho de otro modo, C es el centro de gravedad del sistema. Supongamos que el momento estático se definiera como P×Db, entonces se puede ver fácilmente, tal como lo señala Assis (2008), como el equilibrio no es modificado ya que la igualdad se mantiene:

Según el punto de vista de los críticos de Mach, la consideración de simetría y el concepto de centro de gravedad son los elementos esenciales que permiten a Arquímedes realizar la deducción y no la dependencia lineal con la distancia. Como ya hemos dicho, el Corolario 2 de la Proposición 5, así como el Postulado 6 son las claves de la demostración. Aceptando esto, la dependencia lineal del "efecto perturbador del equilibrio", tal como llama Mach al concepto de momento estático, queda demostrada en la deducción de Arquímedes y no está supuesta implícitamente.

Es importante destacar que Mach aceptó las críticas, especialmente las de Valiati, y al mismo tiempo defendió su posición:

5 Jordano Nemorario y la ciencia de los pesos medieval

Los medievales se encontraron con diferentes tradiciones antiguas acerca de la estática y de la dinámica y realizaron el intento de armonizarlas (cf. Solís & Sellés, 2005). Existía un enfoque geométrico (formal) y otro físico (los materiales con sus tendencias naturales al movimiento). Como hemos visto, la tradición geométrica de Arquímedes poseía una organización matemática impecable pero dicho rigor se alcanzaba con el costo de recurrir a principios formales de indiferencia en situaciones de simetría. Por otra parte, existía la tradición peripatética de los Problemas mecánicos (pseudo-Aristóteles), que se basaba en una teoría física de la dinámica de los cuerpos, pero que estaba formulada en forma confusa desde el punto de vista matemático. En esta tradición, uno de los principios fundamentales es el hecho de que los cuerpos pesados se mueven, si no hay impedimentos, hacia el centro del universo. Es decir, hacia el centro de la Tierra. Si un cuerpo está vinculado a un sistema mecánico, su tendencia natural se ve afectada, de manera tal que conserva parte de su movimiento natural vertical y adquiere un movimiento horizontal violento.

En el Islam, se combinaron ambas tradiciones en lo que se llamó "ciencia de los pesos". Thãbit ibn Qurra escribió, en el siglo IX, un libro sobre la balanza romana (de brazos desiguales), utilizando la tradición dinámica peripatética y con demostraciones matemáticas (cf. Folkerts & Lorch, 2007). Prescindió de los movimientos circulares de los extremos de la palanca alrededor del fulcro y concentró su atención a los desplazamientos verticales (cf. Solís & Sellés, 2005). Utilizó el principio de los desplazamientos virtuales según el cual, si una fuerza eleva a un peso P hasta una altura H, la misma fuerza elevará un peso kP hasta una altura H/k.

En lenguaje moderno, deberíamos llamar a este principio de los trabajos virtuales ya que lo que afirma es la equivalencia entre el producto P×H y el producto kP×H/k. Efectivamente el producto P×H es el trabajo, tal como se lo entiende actualmente, que realiza un fuerza para elevar un cuerpo de peso P hasta una altura H, siendo la velocidad inicial igual a la final. El principio de Thãbit ibn Qurra permite deducir la ley de la balanza romana.

En el siglo XII, la obra fue traducida por Gerardo de Cremona con el título Liber charastonis (Libro de la balanza de brazos desiguales). También se conocieron, para la misma época, los Problemas mecánicos y se tradujeron las obras de Arquímedes. A principios del siglo XIII, se realizó la traducción de un texto griego de autor desconocido de tradición arquimediana con el título De canonio (De los cánones), una obra que tuvo gran influencia. Nos enfrentamos con el encuentro de dos tradiciones, la dinámica del Liber charastonis y la arquimediana-euclídea de De canonio.

Jordano Nemorario (ca. 1220) intentó compatibilizar las dos tradiciones en su obra Elementa Jordani super demostrationem ponderum (Elementos de Jordano para las demonstraciones de los pesos). Comienza planteando siete postulados, a la manera de Arquímedes, pero cuyo contenido es básicamente aristotélico:

En el Postulado 1, podemos apreciar el carácter teleológico del movimiento natural, tomado de la física de Aristóteles. El carácter aristotélico del Postulado 2 es evidente pero podemos decir que, en dicho postulado, no se dice explícitamente que la velocidad es directamente proporcional al peso. Tan sólo podemos interpretar, por ahora, que este postulado dice que el cuerpo más pesado llegará antes que el menos pesado, es decir, en menor tiempo. El Postulado 3 se puede interpretar fácilmente para el caso de un cuerpo apoyado en un plano inclinado. Si el peso del cuerpo para el movimiento vertical es P (su gravedad en el descenso), en un plano inclinado su gravedad en el descenso será P' < P.

El Postulado 4 define el concepto de gravedad según la posición, pero para ello se requiere la definición de oblicuidad. Ésta se da en el Postulado 5, que es una mera definición. Debemos observar aquí que el concepto de oblicuidad (inclinación) está tomado respecto a la vertical, es decir, en forma contraria a como lo hacen los libros modernos de física. Así, la línea vertical tiene para Jordano oblicuidad nula y en ella la gravedad según la posición es el peso P. Una línea inclinada cierto ángulo respecto a la vertical tiene cierta oblicuidad que hace que la gravedad según la posición sea menor que P. Podemos aventurarnos a inferir que, para Jordano, una línea horizontal tiene oblicuidad máxima y en ella la gravedad según la posición sería nula. Dicho de otro modo, para Jordano un cuerpo apoyado en una superficie horizontal tendría su tendencia natural al descenso "anulada". De cualquier modo para poder aplicar el Postulado 4 a diversas situaciones, debería aclararse, en la definición de oblicuidad (Postulado 5), qué quiere decir "para la misma distancia".

El Postulado 6 se adecúa perfectamente al caso de la balanza desequilibrada. Si uno de los cuerpos asciende, en contra de su tendencia natural, es porque está "obligado" por el descenso de otro que es más pesado. El Postulado 7 se puede interpretar como una forma de expresar parte del Postulado 1 y la Proposición 1 de Sobre el equilibrio de los planos de Arquímedes. El Postulado 1 de Arquímedes establece que "pesos iguales a distancias iguales están en equilibrio" y la Proposición 1 dice que "pesos que se equilibran a iguales distancias son iguales". Por lo tanto, la igualdad de pesos y distancias es condición necesaria y suficiente para el equilibrio de la palanca.

5.1 El plano inclinado

Vamos a aplicar la teoría de Jordano al caso del plano inclinado. Sean dos planos inclinados de igual longitud L, como se ilustra en la figura 8, e interpretemos esta igualdad de longitudes como "la misma distancia". Para ello, las longitudes L de ambos planos serán iguales al radio de la circunferencia. Entonces, "para la misma distancia", el plano de altura H2 al participar menos de la vertical tiene mayor oblicuidad. El plano de altura mayor H1 al participar más de la vertical es menos oblicuo, es decir, más próximo a la vertical.

Por lo tanto, la oblicuidad² 2 Utilizando trigonometría podemos ver que la oblicuidad de Jordano es la secante del ángulo b que forma el plano inclinado con el plano vertical. Entonces el peso según la posición sería P' = P/sec b. queda determinada por L/H y se puede ver que se cumple:

Los dos rectángulos negros de la figura 8 representan cuerpos de igual peso apoyados en los planos inclinados. El cuerpo apoyado en el plano de menor altura, más oblicuo, tiene menor gravedad según la posición. El cuerpo apoyado en el plano de mayor altura, menos oblicuo, tiene mayor gravedad según la posición.

En la opinión de Solís y Sellés (2005), lo más original del tratado de Jordano y a la vez de toda la mecánica medieval es el establecimiento, por primera vez, de la ley del plano inclinado. En primer lugar, Jordano, en su Proposición 9, establece que la gravedad según la posición es la misma en todos los puntos del plano. En efecto, para una longitud (o distancia) dada sobre el plano, en cualquier posición le corresponde el mismo segmento horizontal y el mismo vertical. Esto significa que la oblicuidad de un plano inclinado es constante a lo largo del mismo.

A continuación, en la Proposición 10, demuestra que dos pesos ubicados en planos inclinados de diferente inclinación tienen la misma "fuerza de descenso", si se verifica entre ellos que la proporción entre los pesos es igual a la proporción entre las longitudes de los planos.

La demostración de Jordano es casi completamente geométrica como veremos a continuación. Sean dos planos inclinados DC y DA de igual altura y distintas longitudes L1 y L2 respectivamente. Sobre cada uno de ellos está apoyado un cuerpo. Sobre DC un cuerpo de peso P1 y sobre DA un cuerpo de peso P2. Esto se puede apreciar en la figura 9, donde se ha incluido una cuerda que vincula a los cuerpos. Es importante hacer notar que en la demostración de Jordano los cuerpos son puntuales. Es decir, siguiendo la tradición de Arquímedes, los cuerpos son reemplazados por sus centros de gravedad.

Lo que afirma la ley de Jordano es que si la proporción de los pesos es igual a la proporción entre las longitudes, la "fuerza del descenso" (o gravedad según la posición) para ambos cuerpos será la misma y, por lo tanto, si están vinculados por una cuerda, permanecerán en equilibrio.

La demostración requiere la construcción geométrica adicional de otro plano inclinado auxiliar DK de longitud L1 y sobre el cual descansa un cuerpo auxiliar de peso P3 =P1 ubicado en G. Luego se supone que el cuerpo P1 desciende sobre el plano DC una distancia d o verticalmente una altura h1. Por lo tanto el cuerpo P2 se ve obligado a ascender sobre el plano DA la misma distancia d, lo que equivale a subir verticalmente una altura h2, como podemos ver en la figura 10.

Analizando la figura 10 se puede apreciar que la proporción entre h1 y d es la misma que entre DB y DK, ya que DB = H. Análogamente se puede ver que la proporción entre h2 y d es la misma que entre H y DA. De estas dos últimas relaciones, Jordano concluye que h2 es a h1 como L1 es a L2. Entonces:

es decir, si P1 descendiera verticalmente una altura h1, el cuerpo de peso P2, ubicado en el plano de menor oblicuidad, debería subir una altura h2 mayor que h1. La relación entre estos desplazamientos verticales debería ser: h2/h1 = L1/L2. (Recordemos que menor oblicuidad para Jordano es lo que para nosotros sería mayor inclinación.) Por hipótesis, la proporción de los pesos es igual a la proporción entre las longitudes. Entonces:

Pero P1 no puede elevar a P3 hasta la altura h1, tampoco podrá elevar a P2 hasta la altura h2. Podemos apreciar como Jordano aplica el principio de Thãbit ibn Qurra (que también se conoció como el axioma de Jordano), según el cual si una fuerza P1 eleva a un peso P3 hasta una altura h1, la misma fuerza elevará un peso kP3 hasta una altura h1/k. En este caso, P1 es igual a P3 y no puede elevarlo, y k = L2/L1 por lo que kP3 es igual a P2 y este peso tampoco podrá ser elevado. En consecuencia tanto P1 como P2 no se desplazarán si la proporción entre ellos es igual a la proporción entre las longitudes.

Hemos visto, en este ejemplo, como con la geometrización se logra deducir a partir de la física los principios de la estática. A diferencia del planteo estático-geométrico donde la deducción parte de una situación de equilibrio dada, aquí podemos ver como la ley que rige un estado de equilibrio se deduce al suponer un posible desplazamiento (o velocidad virtual) "compatible con los vínculos", como se dice en el lenguaje de la mecánica racional. Según Solís y Sellés:

6 La contribución del Renacimiento: Tartaglia y Guidobaldo

La obra de Jordano, que comentamos en la sección anterior, forma parte del gran despertar cultural de los siglos XII y XIII en el que se pueden encontrar llamativos precedentes para el renacimiento de la matemática (cf. Rose, 1975). Los traductores pre-humanistas de este período llevaron a cabo un inmenso programa de traducción de las ciencias griega y árabe. Algunas de estas versiones jugaron un importante rol en el posterior renacimiento de la matemática. Los trabajos de Fibonacci y de Jordano atestiguan el surgimiento de la invención matemática. En el siglo XVI, se dieron en Italia dos escuelas mecánicas inspiradas en autores de la Antigüedad (cf. Solís & Sellés, 2005).

Fueron estos últimos que, con ensayos que se basaban en conceptos poco claros y principios nada obvios, comenzaron a lograr algunas generalizaciones empíricas que tenían la capacidad potencial de describir y explicar fenómenos dinámicos. De esta manera, iniciaron eficazmente la crítica a la física peripatética. Por el contrario, los de Urbino, al considerar a la física (dinámica) aristotélica irrelevante, no chocaron con ella.

Uno de los más importantes restauradores de las matemáticas, Niccolò Tartaglia (1500-1557) publicó Quesiti ed inventioni diverse (Quesitos e invenciones diversas) en 1546. En el libro VIII de dicha obra, consagrado a la crítica de algunos problemas clave de los Problemas mecánicos (pseudo-Aristóteles), no rechaza los contenidos pero sí cuestiona la ausencia de principios rigurosos. Considera que para que los Problemas mecánicos sean inteligibles es necesario el estudio de la ciencia de los pesos de Jordano.

Los escritores arquimedianos del siglo XVI rechazaron las demostraciones de Tartaglia y, de hecho, toda la tradición de Jordano. Benedetti, que fue alumno de Tartaglia, encontró el teorema del plano inclinado de Jordano como "indigno". El Restaurator mathematicorum (Restaurador de las matemáticas) Commandino, fundador de la escuela de Urbino, desaprobará la tradición de Jordano y Tartaglia. Guidobaldo dal Monte, para quien "Commandino brilló como el sol en el medio de la oscuridad", manifestará su disgusto por la demostración de Jordano, pero aceptará en cambio la demostración errónea de Pappo de Alejandría.

Guidobaldo dal Monte publica su Liber mechanicorum (Libro de las mecánicas), una obra sobre mecánica de rigor desconocido desde los tiempos de Arquímedes, gracias a que prescindía de la dinámica del movimiento. Al considerar que la potencia que mueve una resistencia es superior a la que equilibra supuso que a la dinámica y a la estática le correspondían principios distintos (cf. Solís & Sellés, 2005). El Libro de las mecánicas fue publicado en Pesaro en 1577. Luego fue traducido al italiano en 1581 y posteriormente reimpreso en Venecia en 1615. Gozó de una amplia circulación y fue considerado por sus contemporáneos como la obra más autorizada y sistemática sobre estática desde la época de los griegos (cf. Rose, 1975). Fue entendido como un retorno a los modelos arquimedianos clásicos de pruebas matemáticamente rigurosas y representó la clave del resurgimiento de Arquímedes. En su dedicatoria al Duque Francesco María II de Urbino en la edición de 1577, el mismo Guidobaldo trató de ubicar su obra en el contexto del renacimiento de las matemáticas. Comienza por considerar a Pappo de Alejandría como un discípulo de Arquímedes. El libro VIII de las Colecciones matemáticas de Pappo contiene la aplicación de la ley de la palanca de Arquímedes a las otras máquinas simples. Guidobaldo, por lo tanto, al revivir a Pappo está restituyendo a Arquímedes.

La dedicatoria ya mencionada está consagrada al punto de vista según el cual la mecánica, siendo una ciencia mixta, debe referirse a fenómenos físicos y que no debe permanecer simplemente como una ciencia abstracta y contemplativa. Para Guidobaldo, "la mecánica no puede seguir llamándose mecánica cuando es abstraída y separada de las máquinas" (Guidobaldo apud Rose, 1975, p. 231) y no se conforma con pedir que la ciencia de la mecánica se ocupe de las máquinas, si no que insiste en que los mecánicos mismos se involucren en los asuntos prácticos concernientes a las máquinas reales. Con cierto espíritu baconiano, Guidobaldo afirma que la nobleza de la mecánica consiste en que ésta le da al hombre el control del reino de la naturaleza. Su enfática defensa de la mecánica se basa también en el hecho de que Arquímedes fue un infatigable inventor y que esta actividad fue una parte natural de su interés en la mecánica teórica (cf. Rose, 1975).

Guidobaldo apreciaba a Galileo, a quien recomendó en forma reiterada para puestos universitarios, por la pericia que había mostrado probando teoremas sobre centros de gravedad. Galileo no renunciaba a conectar la tradición estática y dinámica mediante consideraciones que permitieran pasar de manera continua de condiciones de equilibrio al movimiento utilizando los mismos principios, pero a la vez consideraba posible fundamentar en forma rigurosa y geométrica el estudio del movimiento. De esta manera llegó a pensar que una fuerza insensible podría poner en movimiento a un cuerpo inicialmente en reposo en un plano horizontal. De aquí se podría pensar que un cuerpo podría mantenerse indefinidamente en movimiento sobre una superficie horizontal, si se prescinde de la fricción, empujado por una fuerza insensible.

Guidobaldo en cambio consideraba que había allí un cambio radical de situación física. Por esta razón rechazó el teorema correcto del plano inclinado de Jordano y adhirió al erróneo de Pappo. En efecto, la Proposición 9 del libro VIII de las Colecciones matemáticas de Pappo está planteado en forma de problema y dice: "para arrastrar un peso dado sobre un plano horizontal es necesaria una fuerza dada. Se requiere hallar la fuerza necesaria para arrastrar a dicho peso hacia arriba sobre un plano inclinado que forma cierto ángulo con el plano horizontal" (Cohen & Drabkin, 1958, p. 194). En la demostración de Pappo:

Pero se llega a un resultado incorrecto debido a que no tuvo la habilidad de descomponer el peso en dos componentes, paralela y perpendicular respectivamente, al plano inclinado. Un procedimiento que recién estaría disponible a partir de las demostraciones de Stevin y de Galileo, cerca de 1600 (cf. Mach, 1949).

7 Galileo y la nueva dinámica

Galileo Galilei (1564-1642) se convirtió en matemático en la década de 1580 y se unió a la gran ola del renacimiento de la matemática. Las obras de Tartaglia y Commandino estaban en amplia circulación; Bennedetti publicó Liber diversarum especulationum (Libro de las varias especulaciones) en 1585; y el Libro de las mecánicas de Guidobaldo ya había aparecido tanto en latín como en italiano. Mientras la ciencia de la estática había quedado firmemente establecida en el marco arquimediano, la dinámica se resistía a tal trasformación desde los tiempos de Arquímedes mismo. Tanto Tartaglia como Benedetti habían logrado sólo algunos buenos resultados en algunos aspectos aislados de la dinámica y esto parecía confirmar la dificultad de establecer una dinámica matemática general arquimediana. La crisis se puso de manifiesto cuando Guidobaldo en 1577 denunció los intentos de reducir la ciencia de la mecánica a los principios arquimedianos que rigen a la estática. Para Guidobaldo la dinámica permanecía como una ciencia obstinadamente física que debía ser explicada en términos de causas y efectos cualitativos. Mientras prevaleciera esta perspectiva, no habría una ciencia mecánica unificada y, en consecuencia, no habría física moderna. Galileo logró resolver la crisis y conducir al renacimiento de la matemática a una conclusión exitosa (cf. Rose, 1975).

Las primeras obras científicas de Galileo fueron Theoremata circa centrum gravitatis (1585) y La bilancetta (1586). La primera de estas obras mereció la aprobación de Guidobaldo que comenzó a apoyarlo académicamente. Con poco más de veinte años, Galileo empezó a moverse con soltura en las tradiciones prácticas tipo Tartaglia y en las más rigurosas al estilo de Guidobaldo (cf. Solís & Sellés, 2005). En 1589, ocupó la cátedra de matemáticas de Pisa y en 1591 se trasladó a la Universidad veneciana de Padua. En ambas ocasiones fue recomendado por Guidobaldo.

7.1 El movimiento

Posteriormente redactó De motu (1589-1592) cuyo propósito explícito es analizar y criticar la doctrina peripatética acerca de los movimientos naturales y violentos. Empleando métodos de análisis tomados tanto de la estática como de la hidrostática de Arquímedes, Galileo intentó construir una dinámica general, válida para todo tipo de movimientos (cf. Navarro, 1991). Debemos destacar que, en esta obra, Galileo comienza aceptando la cosmología aristotélica de los cuatro elementos y la física basada en los lugares naturales. Sin embargo su concepción del peso es diferente y por lo tanto también habrá diferencias en toda explicación dinámica que lo tenga como su causa (cf. Molina, 2005). Para Galileo, en lo que respecta a la mecánica, todos los cuerpos están hechos de una misma materia. No existe la liviandad natural. Todos los cuerpos tienden hacia abajo. Cuando un cuerpo asciende es porque su densidad es menor que la del medio (cf. Solis & Sellés, 2005). Dado que los cuerpos livianos ubicados en un medio más pesado ascienden por extrusión y no en razón de una propiedad natural que les sea propia, se infiere que no habrá movimientos ascendentes naturales y que el único movimiento rectilíneo natural será el movimiento descendente hacia el centro de la Tierra. Es decir, la "levedad" hay que entenderla en un sentido relativo: son livianos aquellos cuerpos cuyo peso específico es menor que el del medio. En este marco conceptual, la velocidad de caída sería directamente proporcional a la diferencia de pesos específicos. Resumiendo: "pesado" y "liviano" ya no son cualidades absolutas sino que se han transformado en relaciones (cf. Koyré, 2001).

Galileo reconoce que esta regla, propuesta para determinar la velocidad de caída, no está corroborada experimentalmente y además señala la dificultad empírica que significa reconocer que dicha velocidad no es constante. Para resolver esta dificultad, Galileo procede al estudio de los movimientos violentos y de la explicación de éstos obtendrá una analogía para justificar la aceleración en los movimientos naturales (cf. Navarro, 1991).

Galileo no puede evitar la obligación de justificar la incongruencia entre la propia teoría de los movimientos naturales uniformes y el dato experimental de la aceleración. Dado que Galileo enfatiza que en el movimiento natural no hay variación ni en la gravedad del móvil, ni en la del medio, la aceleración debe depender de factores externos que operan sobre la gravedad del móvil. La solución viene dada por la virtus impressa empleada para justificar los movimientos violentos.

Tomemos el caso de una piedra que se lanza en el aire verticalmente hacia arriba. La piedra sube; por lo tanto, podemos decir que ha adquirido cierta cualidad (o virtud) que la hace subir. Como el hecho de elevarse es una propiedad de los cuerpos leves, lo que la piedra ha adquirido es levedad. Esta levedad es una virtus impressa no natural. Esta virtud motriz (levedad) se mantiene en la piedra privada del contacto con el motor³ 3 Recordemos que para la física aristotélica no puede haber movimiento sin motor y el motor debe estar en contacto con lo movido. de forma análoga a como se conserva el calor en el hierro luego de haber sido retirado del contacto con el fuego. Esta virtud impresa por la acción del lanzamiento se va debilitando progresivamente en el objeto lanzado, una vez separado del agente lanzador, de forma análoga a como el calor "disminuye" al ser retirado del contacto con el fuego. La virtud motriz es algo impreso al objeto pero además es algo cuyo ser consiste en actuar. Ahora bien, al producir este movimiento ascendente, la levedad, como toda fuerza impresa, se agota por y en su misma acción.

La dinámica de Galileo contenida en su obra De motu permite la existencia de movimientos neutros, ni naturales ni violentos, ya que no van en contra ni a favor de la gravedad. En una superficie horizontal equidistante del centro de la Tierra un cuerpo está en un estado indiferente respecto al movimiento. Galileo sostiene, en contra de Pappo y de Guidobaldo, que una fuerza insensible alcanza para poner en movimiento un cuerpo en esas condiciones.

La demostración de Galileo comienza por considerar que un cuerpo apoyado sobre un plano apenas inclinado respecto al horizonte descenderá naturalmente si no hay ninguna resistencia externa. Esto se puede apreciar claramente en el caso del agua. Un cuerpo ascenderá por dicho plano inclinado sólo violentamente. Pero en un plano horizontal no se moverá ni natural ni violentamente. Por lo tanto se puede probar que con una fuerza mínima se puede poner en movimiento. Aceptemos que cualquier grave puede moverse sobre un plano horizontal por medio de una fuerza menor que la necesaria para moverse por un plano inclinado.

En la figura 11, AB representa al plano del horizonte y CB una recta vertical. El móvil es una esfera de peso P. El segmento indicado con f representa la magnitud de una fuerza cualquiera. El segmento indicado con F represen-ta la magnitud de la fuerza capaz de elevar a la esfera verticalmente. Supongamos que F es a f como AD es a BD.⁴ 4 Aquí, Galileo está utilizando la ley del plano inclinado, cuya primera demostración correcta se atribuye a Jordano Nemorario (ca. 1220) quien utilizara el principio de los trabajos virtuales de Thabit ibn Qurra. Es decir:

Entonces, si F puede elevar a la esfera verticalmente, f < F podrá hacerlo sobre el plano inclinado AD. Por hipótesis la esfera podrá ser movida por el plano horizontal AB por medio de una fuerza menor que f. En esta demostración, la fuerza f se puede elegir de manera tal que sea muy pequeña, sólo reduciendo la inclinación del plano. Dicho de otro modo achicando su altura H respecto a su longitud L. Como la fuerza necesaria para mover al cuerpo sobre el plano horizontal es menor que f y ésta es tan pequeña como queramos, Galileo está planteando la posibilidad de mover a la esfera por medio de una fuerza que en términos actuales la denominaríamos infinitesimal.

Entonces para Galileo es posible mover sobre una superficie horizontal, es decir equidistante del centro de la Tierra, y prescindiendo del rozamiento, a un grave con movimiento eterno y uniforme (cf. Solís & Sellés, 2005). De este modo, una esfera ubicada en el centro del mundo puede ponerse en movimiento circular uniforme y eterno. ¿Y qué es la Tierra sino una esfera ubicada en el centro del mundo? En esta época, en que todavía Galileo no manifestó su adhesión al sistema copernicano, pudo haber empezado a concebir que la Tierra pueda estar animada de movimiento. Es decir, es posible considerar a la Tierra como un cuerpo celeste, especulando sobre su posible movimiento circular, aunque todavía considere que es el centro del universo (cf. Molina, 2005).

7.1 Las lecciones de mecánica, el momento, la palanca (balanza romana) y el plano inclinado

En 1592, Galileo se trasladó a la Universidad de Padua. Se ha hallado documentación que muestra que en el período lectivo 1597-98, los Problemas mecánicos (pseudo-Aristóteles) fueron tema de sus clases. Esta obra atribuida erróneamente a Aristóteles fue casi desconocida durante la Edad Media, pero en el siglo XVI fue traducida a varias lenguas y tuvo una amplia circulación (cf. Molina, 2005).

Allí redactó varias versiones de un nuevo tratado dedicado al estudio de las máquinas simples titulado Le mecaniche (Las mecánicas) (cf. EN, 2, p. 155-90). Esta obra pudo haber sido utilizada por Galileo para sus clases en la Universidad pero es más probable que hayan estado destinadas a sus clases particulares (cf. Molina, 2005). En dicha obra, la situación estática simplificada de la tradición arquimediana se amplía al considerar fuerzas insensibles capaces de romper el equilibrio. Galileo considera que la fuerza natural y general para todos los cuerpos es la gravedad pero en una máquina el movimiento efectivo de un cuerpo no depende sólo de ella. Es esencial para la explicación de movimiento la ubicación del centro de gravedad de todo el sistema. Galileo introduce el concepto de momento para designar a la efectividad de la fuerza según los movimientos posibles (cf. Solís & Sellés, 2005). Este concepto incluirá al de gravedad según la posición que Jordano ya había utilizado en su deducción de la ley del plano inclinado y también al bien conocido momento de una fuerza. Este concepto implica para Galileo una renovación del propio léxico y tiene una notable importancia ya que parece abrir la puerta a la posibilidad de una derivación de la dinámica a partir de los propios principios de la estática (cf. Molina, 2005).

7.1.1 el momento

Le mecaniche comienza con una introducción dedicada a "la utilidad que se obtiene de la ciencia de la mecánica y de sus instrumentos" (EN, 2, p. 155). A continuación Galileo define gravedad, momento y centro de gravedad. Interesa señalar la definición de momento:

Como podemos apreciar, aunque no se lo exprese en forma simbólica, en estas palabras de Galileo podemos encontrar la definición de momento de una fuerza con respecto a un punto. El ejemplo de la balanza romana es más que claro para darse cuenta que se está refiriendo al producto del peso por la distancia desde el punto de suspensión del mismo hasta el fulcro. Pero por si este concepto no hubiera quedado suficientemente claro, Galileo introduce una razonable suposición, que consiste en replantear el Postulado 1 y la Proposición 1 de Arquímedes, y nos aclara cómo se debe calcular el momento:

7.1.2 la palanca (o balanza romana)

A continuación Galileo desarrolla, en Las mecánicas, una brillante y detallada demostración de la ley de la palanca que en sus rasgos esenciales responde al espíritu de la original de Arquímedes. Varias décadas después (ca. 1630) reproducirá dicha demostración en la Jornada Segunda de los Discorsi de 1638 (cf. EN, 8; Galilei, 1945). En efecto, en dicha obra, Salviati, el portavoz de Galileo, dice:

Si bien Galileo desarrolla su demostración en Las mecánicas utilizando el típico rigor geométrico arquimediano, a continuación sostiene como argumento en defensa de la ley de la palanca ideas bastante similares a las expuestas en Problemas mecánicos (pseudo-Aristóteles). En "Algunas advertencias a cerca de las cosas dichas" (EN, 2, p. 163-4), Galileo nos muestra claramente su aceptación de las dos tradiciones, tanto la representada, entre otros, por Commandino y Guidobaldo y que podríamos denominar "estática-arquimedeana", como la posición menos "rigurosa" y "dinámica", representada por Tartaglia y Benedetti. Así, cuando se trata de la demostración matemática recurre a Arquímedes pero luego utiliza los argumentos dinámicos con los que "pueden razonablemente confirmar la misma verdad" (EN, 2, p. 163).

Para pasar de la situación de equilibrio a la de desequilibrio es suficiente con agregar a uno de los pesos, por ejemplo, el B, un peso insensible y, por lo tanto, se lo puede considerar nulo y sin embargo analizar el fenómeno dinámico: "no tendremos en cuenta esa cantidad insensible y no distinguiremos entre poder un peso sostener a otro y poderlo mover" (EN, 2, p. 164).

Lo que "se gana" en fuerza (peso) "se pierde" en desplazamiento. El cuerpo más pesado A recorre, al subir, un arco menor mientras que el cuerpo menos pesado B, al descender, recorre un arco mayor. Entonces para que A pueda subir desde A hasta D, es necesario que el cuerpo menos pesado B, descienda más que lo que sube A como podemos ver en la figura 13. Encontramos en este fragmento de Las mecanicas de Galileo un antecedente del concepto de trabajo. Podríamos decir que el trabajo realizado por B al descender cierta altura consiste precisamente en hacer subir al peso mayor A pero a una altura menor. Si bien esto no lo dice Galileo, si nosotros no distinguimos entre el desplazamiento vertical y el desplazamiento por el arco de circunferencia, la analogía es perfecta. Por lo tanto si repetimos el razonamiento de Galileo para el caso de pequeños desplazamientos en donde la longitud del arco y el desplazamiento vertical miden casi lo mismo, estaríamos en presencia de una aplicación del principio de los trabajos virtuales que en cierto modo ya había sido anticipado en la Edad Media por Thãbit ibn Qurra y que fuera utilizado con éxito por Jordano en su deducción de la ley del plano inclinado.

Como el ascenso de A y el descenso de B ocurren en el mismo lapso de tiempo, entonces B se mueve más rápido que A. Por lo tanto, se puede asignar un significado adicional al concepto de momento incluyendo el efecto de la velocidad. El peso B es menor que A pero su mayor velocidad le incrementa el momento, es decir su efectividad:

Si partimos de la situación con la balanza desequilibrada y agregamos al peso A un peso insensible, entonces el movimiento se invierte. El peso A al descender desde D hasta A "hace trabajo" que consiste en permitir que B vuelva a subir desde E nuevamente hasta B. Pero esto lo puede hacer ganándole en fuerza a B, ya que A pesa más que B, pero con el costo de que su movimiento es más lento que el de B: "Y así recíprocamente, colocado el peso A en D y el otro en el punto E, no estará fuera de razón que aquél pueda, cayendo lentamente hacia A, levantar velozmente el otro a B, restaurando con su pesantez lo que por la lentitud de su movimiento viene a perder" (EN, 2, p. 164).

7.1.3 El plano inclinado

Las mecánicas es un tratado sobre las máquinas simples. En esta obra, Galileo realiza su propia demostración de la ley del plano inclinado. Luego de consideraciones muy similares a las que ya había expuesto en Del movimiento respecto al movimiento de los cuerpos sobre superficies inclinadas y antes de proceder a la demostración de la ley, establece: "...podemos tomar como axioma indudable esta conclusión: los cuerpos graves, eliminados todos los impedimentos externos y adventicios, pueden ser movidos en el plano del horizonte por cualquier fuerza mínima" (EN, 2, p. 180; énfasis mios). Hemos subrayado para que recordemos que anteriormente mostramos como Galileo demuestra esta afirmación utilizando la ley del plano inclinado, pero ahora la considera un axioma.

A continuación explicaremos la demostración, dentro de la cual Galileo hace referencia a la antigua y errónea de Pappo admirada por Guidobaldo, en estos términos:

Galileo comienza su demostración con el trazado de una circunferencia cuyo diámetro horizontal es AC y su centro es B. En los extremos de este diámetro, hay dos pesos iguales como si A y C fueran lo extremos de una balanza o palanca y B entonces sería el fulcro o punto de apoyo. En estas condiciones, ambos pesos tienen igual momento y, por lo tanto, la palanca está equilibrada. Pero se nos invita a suponer que el brazo BC se puede inclinar como si el punto B fuera una articulación. Si el brazo BC pasa a ocupar ahora la posición BF el peso en su extremo F tiene ahora menor momento ya que la distancia BK es menor que la distancia BC.

Si trazamos una recta GFH perpendicular en F a BF, es decir una recta tangente a la circunferencia en F, el peso en F se comporta como si estuviera colgado de la línea KB que es menor que AB. Los pesos en A y en F son iguales pero el momento del peso ubicado en F es menor que el momento de peso ubicado en A en la misma proporción en que BK es menor que AB.

Si suponemos una inclinación mayor del brazo BF incrementando el ángulo KBF, la recta tangente tendrá una inclinación menor respecto a la horizontal y, por lo tanto, el momento del peso en el extremo F será aún menor que antes. Si el peso ubicado inicialmente en C lo desplazamos hacia abajo pero manteniendo siempre la misma distancia respecto a B (es decir el radio de la circunferencia) su momento va disminuyendo a medida que se va acercando al punto más bajo pasando por distintas posiciones F. Entonces, se puede pensar que el peso ya no está vinculado por medio del brazo articulado en B, sino que desliza apoyado sobre una rampa circular y a medida que desciende su momento disminuye.

A partir de la definición de momento, de la analogía con la balanza y de una ingeniosa construcción geométrica, Galileo concluye su razonamiento:

Podemos apreciar que la definición de momento dada al inicio de Las mecánicas es lo suficientemente amplia como para incluir al momento de una fuerza con respecto a un punto, es decir, fuerza por distancia, como así también a la tendencia a ir hacia abajo según la posición similar al concepto utilizado por Jordano. De esta manera el argumento de Galileo se puede resumir, observando la figura 15, de la siguiente manera:

Cuando el móvil está en C, el momento:

Cuando el móvil está en el punto F, el momento:

La demostración de Galileo concluye con una clara enunciación de la ley del plano inclinado:

No debemos olvidarnos que este tratado versa sobre las máquinas simples y, por lo tanto, "finalmente, no debe silenciarse la consideración que desde el principio se ha dicho, que es necesario mantener en todos los instrumentos mecánicos, a saber, que lo que se gana en fuerza por su medio, otro tanto se pierde en tiempo y en velocidad" (EN, 2, p. 183).

Entonces, si un cuerpo F desciende verticalmente empujando sobre el plano inclinado al móvil de peso P, ambos recorrerán la misma distancia, uno verticalmente, el otro sobre la superficie oblicua. Pero aunque el móvil P haya recorrido toda la línea de longitud L en el mismo tiempo que el otro F haya recorrido igual longitud, "no obstante el grave P no se habrá alejado del centro común de las cosas graves más que lo que le corresponde a la perpendicular" de longitud h.

Pero el grave F ha descendido toda la longitud L para poder elevar al grave P sólo la altura h. Por lo tanto, como consecuencia de la ley del plano inclinado (F : L :: h : L), podemos fácilmente concluir que la fuerza F es menor que P pero para poder elevar a P hasta una altura h debe recorrer una distancia L mayor que h. En nuestra terminología actual, el trabajo (o sea, elevar a P hasta la altura h), que realiza la fuerza F (fuerza por distancia recorrida,⁶ 6 Mientras que el momento es fuerza por distancia, pero dicha distancia se mide desde la recta de acción de la fuerza hasta el centro de momentos. F×L) es igual al producto del peso P por el recorrido vertical h del móvil P.

8 Comentarios adicionales y conclusiones

8.1 Enseñanza, aprendizaje e historia de la física

En la actualidad, cualquier persona con una formación básica en física, comprende y acepta que las leyes de la estática no son más que una consecuencia de las leyes del movimiento enunciadas por Newton. Si, en las ecuaciones dinámicas del movimiento, tanto las aceleraciones lineales como las angulares se igualan a cero, obtenemos las ecuaciones que corresponden al equilibrio de un cuerpo rígido:

. Tanto la sumatoria de todas las fuerzas como la sumatoria de todos los momentos de esas fuerzas son iguales a cero. En efecto, los programas universitarios de enseñanza de la física, en la gran mayoría de los casos, comienzan con nociones de cinemática para luego entrar en el capítulo de la dinámica, en el cual el núcleo central son las tres leyes de Newton y por deducción a partir de ellas, y definiendo nuevos conceptos (cantidad de movimiento, momento de una fuerza, trabajo, energía cinética etc.), se obtienen otras leyes de la mecánica.

Ahora bien, la historia detrás de estos conceptos y leyes es muy distinta a la manera como está estructurada la mecánica clásica en su enseñanza básica y mucha mayor diferencia hay aun en el caso de un curso superior de mecánica clásica racional.

Esta forma de enseñanza apunta a un aprendizaje eficaz para que el futuro profesional adquiera con una economía de recursos las herramientas fundamentales para proseguir con su aprendizaje de la física y de otras disciplinas, pero empobrece la comprensión de dichos conceptos si tenemos en cuenta que ellos son el fruto de una actividad de investigación y reflexión que se ha extendido durante siglos. Como sostiene Lindberg:

En la breve sinopsis que constituye el presente trabajo, pudimos apreciar como las leyes del equilibrio fueron demostradas matemáticamente por Arquímedes en la Antigüedad y vimos cómo esta tradición resurgió con gran impulso durante el Renacimiento. Pero la teoría arquimediana no era considerada como parte de la ciencia física sino como una ciencia mixta, algo así como una rama de las matemáticas. Paralelamente existía la dinámica inspirada en la física aristotélica basada en conceptos clave tales como:

Esta física presentaba serios problemas, si se intentaba formalizar en forma matemática, como no podía ser de otra manera por el lugar que Aristóteles le asignaba a la matemática en su filosofía. Había además otras dificultades de tipo conceptual, por ejemplo, la explicación de movimientos donde no se evidenciaba el contacto entre el motor y el móvil. El caso paradigmático es el movimiento de los proyectiles, para el cual ya en la Antigüedad (siglo VI), Filopón (Juan el Gramático de Alejandría) propuso su teoría de la fuerza impresa: "(...) la idea de que algunas fuerzas son entidades inmateriales independientes de los cuerpos, aunque susceptibles de implantarse en ellos desde fuera" (Solís & Sellés, 2005, p. 119). Cuando se arroja una piedra o una flecha, para Filopón, el lanzador le transmite al proyectil cierta fuerza motriz incorpórea, que permanece en el cuerpo arrojado sin necesidad de que éste tenga contacto con un motor. Esta idea pasó a los árabes en el siglo XII y a los latinos en el siglo XIV, y fue utilizada, entre otros, por Benedetti, discípulo de Tartaglia, y luego por Galileo en Del movimiento (cf. Solís & Sellés, 2005).

Según Koyré (2001), la noción galileana de fuerza impresa fue tomada de Benedetti. Pero posteriormente otros trabajos de investigación permitieron aclarar la distinción entre la virtus impressa (autoextinguible) y el ímpetus (protoinercial) de Buridan y Benedetti. Como hemos visto, Galileo en Del movimiento, utiliza el primero de estos conceptos, que casi con seguridad fue tomado de Ibn Bayya (Avempace) y que había aprendido de su profesor en Pisa, Girolamo Borro (cf. Molina, 2005).

En este trabajo hemos podido apreciar como ciertos conceptos fundamentales de la mecánica clásica, que habitualmente se consideran como consecuencias de la mecánica newtoniana, tienen una larga historia detrás. En particular, hemos visto como al estudiar el germen de conceptos tales como el momento de una fuerza y el trabajo, se manifiesta entre ellos cierto parentesco. Sin embargo, las definiciones en los libros de texto no sugieren una relación entre ellos.

El concepto de trabajo ya está claramente sugerido en el axioma de Jordano y fue utilizado para la demostración de la ley del plano inclinado. A su vez este axioma no es otra cosa que un principio formulado por Thãbit ibn Qurra en su Liber charastonis (cf. Folkerts & Lorch, 2007). Pero en forma mucho más evidente hemos visto la génesis del concepto de trabajo en las lecciones de mecánica de Galileo (cf. Cardwell, 1967).

El concepto de momento de una fuerza está claramente definido por Galileo en dichas lecciones aunque su definición es más amplia que la actual. Lo más interesante es ver cómo utilizó ambos conceptos en su deducción de la ley del plano inclinado:

8.2 El contexto social de la resoluciòn de la crisis entre estática y dinámica

Según el historiador Paul Rose (1975) durante el siglo XV en Italia, la pasión por el redescubrimiento de la Antigüedad clásica guió la rápida formación y crecimiento de grandes bibliotecas humanistas. Estas colecciones humanistas diferían de las bibliotecas medievales tanto en tamaño como en contenido. El contenido de matemáticas griegas, en las bibliotecas de la Edad Media, generalmente se limitaba a traducciones de Euclides y algunas veces de Arquímedes. Las nuevas bibliotecas en la Italia renacentista incluían no sólo a Euclides y Arquímedes, tanto en latín como en griego, sino también textos griegos de Apolonio, Diofanto, Herón y Pappo. Sin todo este material reunido por los humanistas del quattrocento, el renacimiento de la matemática no hubiera sido posible. Pero además muchos de estos coleccionistas tuvieron un fuerte interés en las matemáticas y ellos mismos promovieron activamente las traducciones y el resurgimiento de las matemáticas griegas. De este modo, estas bibliotecas humanistas se convirtieron en importantes centros culturales y, gracias al poderoso impulso recibido por los humanistas del quattrocento, el renacimiento de la matemática fue el logro de matemáticos y no asunto de magos ni de astrólogos.

La interacción entre patrones humanistas y matemáticos en Italia precedió a la revolución científica. Este patronazgo tuvo un efecto de amplio alcance, ya que el patrón podía ocuparse de la seguridad financiera de su protegido y a la vez permitir su desarrollo fuera del ámbito de las universidades. Galileo fue un humanista antes de ser un matemático. Pasó algunos años de su juventud dedicado a los estudios humanistas como lo atestigua Viviani. Fue un exponente claro de esta nueva cultura renacentista que tuvo también, según Paul Rose (1975), una importante influencia psicológica, que contribuyó en gran medida al resurgimiento de la matemática.

Y fue Galileo quien logró resolver la crisis entre estática y dinámica, quien llevó el renacimiento de la matemática a una conclusión exitosa (cf. Rose, 1975) y contribuyó al nacimiento de una nueva física (cf. Cohen, 1977).

Fechas de Publicación