Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-18T04:03:47.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Scott's interpolation theorem fails for Lω1, ω

Published online by Cambridge University Press:  12 March 2014

Henry Africk
Henry Africk*
Affiliation:
New York City Community College, Brooklyn, New York 11201
Get access Rights & Permissions [Opens in a new window]

Extract

In [1] we proved the following interpolation theorem for first-order (finitary) logic:

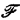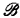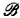Theorem (Scott). Let A and B be sentences. There is an -sentence C such that A → C and C → B iff whenever and are 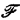-isomorphic structures and 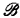satisfies A then 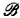satisfies B.

We show here that the Theorem holds for A and B in Lω1, ω only if we permit the interpolant C to be in L(2ω)+, ω, where (2ω)+ is the successor of 2ω.

Our language contains the usual logical symbols and the relation symbols Ri, is i ∈ J. If I ⊆ J define an I-sentence to be a sentence containing only relations with subscripts in I. If 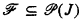define an 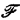-sentence to be a boolean combination of I-sentences with 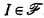, i.e., a sentence consisting of I-sentences, for various I's in 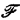, joined together by ∨, ∧ and ⌝; e.g., ∀xR1(x) ∨ ∀xR2(x)is a{{1}, {2}}-sentence but ∀x(R1(x) ∨ R2(x)) is not. If 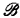is a structure let 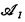, be the structure obtained by restricting 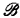to just the relations with subscripts in I. We say that 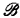is -is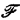omorphic to 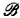if 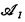is isomorphic to 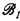for each .

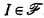Type
Research Article
Information
The Journal of Symbolic Logic , Volume 39 , Issue 1 , March 1974 , pp. 124 - 126
Copyright
Copyright © Association for Symbolic Logic 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Africk, H., A proof theoretic proof of Scott's general interpolation theorem, this Journal, vol. 37 (1972), pp. 683–695.Google Scholar
[2]Feferman, S., Lectures on proof theory, Proceedings of the Summer School in Logic (Leeds, 1967), Lecture Notes in Mathematics, no. 70, Springer-Verlag, 1968, pp. 1–107.Google Scholar
[3]Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas, Fundamenta Mathematicae, vol. 57 (1965), pp. 253–272.CrossRefGoogle Scholar
[4]Malitz, J., Infinitary analogs of theorems from first order model theory, this Journal, vol. 36 (1971), pp. 216–228.Google Scholar
[5]Scott, D., Interpolation theorems, Third International Congress for Logic, Methodology and Philosophy of Science, Amsterdam, 1967 (unpublished).Google Scholar
[6]Scott, D., Logic with denumerably long formulas and finite strings of quantifiers, The Theory of Models (Proceedings of the 1963 International Symposium at Berkeley), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar