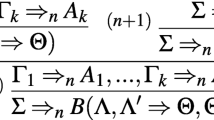Modular Semantics for Theories: An Approach to Paraconsistent Reasoning

Abstract

Some scientific theories are inconsistent, yet non-trivial and meaningful. How is that possible? The present paper aims to show that we can analyse the inferential use of such theories in terms of consistent compositions of the applications of universal axioms. This technique will be represented by a preferred models semantics, which allows us to accept the instances of universal axioms selectively. For such a semantics to be developed, the framework of partial structures by da Costa and French will be extended by a few elements of the Sneed formalism, also known as the structuralist approach to science.

Appendix: Proofs

Proposition 1

Let T be a set of axioms upon which< _s is defined by Definition 9.< _s of T is smooth in the set of L(V )interpretations.

A few further things need to be defined in order to show that < _s is smooth in the set of L(V )interpretations:

Definition 16

Consistent set of applications. A set A of applications $\mathcal {A}_{i,j}$isconsistent iff the set

$$\mathbf{W} = \{W(\mathcal{A}_{i,j})\; |\; \mathcal{A}_{i,j} \in \mathbf{A}\}$$

has a consistentchoice set of local worlds. That is, any member of this choice set is semantically consistent with any othermember. $W(\mathcal {A}_{i,j})$is defined by Eq. 7.

Consistency between worlds is understood as follows:

Definition 17

Consistency between two worlds. Let $w_{i}=\langle A_{i},\mathfrak {a}_{i}\rangle$and $w_{j}=\langle A_{j}, \mathfrak {a}_{j}\rangle$be two total structures, or worlds. w _i is consistent with w _j iff, for all relation symbols $R_{k} \in (dom(\mathfrak {a}^{\prime }) \cap dom(\mathfrak {a}^{\prime }))$,all $m \in \mathbb {N}$,and all m-tuples x, we have (i) if $x \in (R_{k})_{w_{i}}$and $x \in {A_{j}^{m}}$,then $x \in (R_{k})_{w_{j}}$,and (ii) if $x \in (R_{k})_{w_{j}}$and $x \in {A_{i}^{m}}$,then $x \in (R_{k})_{w_{i}}$.(R _k ) _w denotes the relation R _k of the structure w and A ^mthe m-ary Cartesian product of A.

A set of applications $\mathcal {A}_{i,j}$ is inconsistent iff it is not consistent in this sense. Furthermore, we need to define the notion of a maximally consistent set of applications $\mathcal {A}_{i,j}$ of T.

Definition 18

Maximally consistent set of applications. A setA ofapplications $\mathcal {A}_{i,j}$is maximally consistent iff

• (1) the set $\mathbf {W} = \{W(\mathcal {A}_{i,j})\; |\; \mathcal {A}_{i,j} \in \mathbf {A}$}has a consistent choice set of local worlds

• (2) there is no set A ^′such that (i) A ⊂A ^′and (ii) A ^′is a consistent set of applications.

By the definition of < _s , any set C of maximally consistent applications defines a set of < _s -minimal elements. For, by the definition of a maximally consistent set of applications, C satisfies the following two conditions: (i) there is a global world w such that A p p(w) = C, and (ii) there is no global world w ^′ such that C ⊂ A p p(w ^′). Any global world w satisfying these two conditions is < _s -minimal in the set of L(V )interpretations. We prove now the following lemma:

Lemma 1

A set A of applications is inconsistent iff there is a finite set A ^′⊆A that is inconsistent.

This lemma asserts that sets of applications satisfy a certain compactness property. In fact, we can prove this lemma using (syntactic) compactness of first-order logic. In preparation of this proof, recall that, in Section 4.1, we have made the naming assumption for structures $\mathcal {A}_{i,j}$. That is, any object of the domain of $\mathcal {A}_{i,j}$ is designated by a constant term of the global language L(V ). If the set C of constants is uncountable, C contains pseudo constants. Note, however, that the presence of pseudo constants does not invalidate the syntactic compactness theorem (see Enderton [23, p. 135–142]).

Let $Th(\mathcal {A}_{i,j})$ be a syntactic representation of the semantic information of both the partial structure $\mathcal {A}_{i,j}$ and the instance j of α _i . It is defined by the following two conditions:

$$R_{k}(c_{1}, \ldots, c_{k}) \in Th(\mathcal{A}_{i,j})\;\text{ iff}\;\mathcal{A}_{i,j} \models R_{k}(c_{1}, \ldots, c_{k}) $$

and

$$\alpha_{i}^{\prime}[c_{o1}/x_{1}, \ldots, c_{on}/x_{n}] \in Th(\mathcal{A}_{i,j}) \;\text{ iff}\;(o_{1}, \ldots, o_{n})\in A^{n}_{i,j} $$

where α _i is of the form $\forall x_{1} {\ldots } \forall x_{n} \alpha _{i}^{\prime }$ and $\alpha _{i}^{\prime }$ does not begin with a universal quantifier. c _{o i} (1 ≤ i ≤ n) is a constant that designates object o _i . In sum, $Th(\mathcal {A}_{i,j})$ contains the atomic sentences verified by $\mathcal {A}_{i,j}$ and the instance of α _i whose descriptive symbols are (partially) interpreted by $\mathcal {A}_{i,j}$.

We show that the following holds:

Sublemma 1

A is consistent iff $Mod(\bigcup _{\mathcal {A}_{i,j}\in \mathbf {A}} Th(\mathcal {A}_{i,j}))\neq \emptyset$ .

Forward: suppose A is consistent. Then, the set $\mathbf {W} = \{W(\mathcal {A}_{i,j})\; |\; \mathcal {A}_{i,j} \in \mathbf {A}\}$ has a choice set W _c that is consistent in the sense of Definitions 16 and 17. Using this choice set, we can construct a structure $\mathbf {w}=\langle A, \mathfrak {a} \rangle$ such that (a) $A=\bigcup _{w \in W_{c}} Dom(w)$, (b) $dom(\mathfrak {a}) = \bigcup _{\langle A^{\prime }, \mathfrak {a^{\prime }}\rangle \in W_{c}} dom(\mathfrak {a}^{\prime })$, and (c) for any $R_{k} \in dom(\mathfrak {a})$, $(R_{k})_{\mathbf {w}}= \bigcup \{(R_{k})_{w^{\prime }}\;|\;$ there is w ^′∈ W _c such that $w^{\prime }=\langle A^{\prime }, \mathfrak {a}^{\prime } \rangle$ and $R_{k}\in dom(\mathfrak {a}^{\prime })\}$. (D o m(x) designates the domain of the structure x, $dom(\mathfrak {a})$ the domain of the interpretation function $\mathfrak {a}$, and (R _k ) _x the relation R _k of the structure x.) Hence, (i) there is a structure w such that, for all $\mathcal {A}_{i,j}\in \mathbf {A}$, there is a local world $w\in W(\mathcal {A}_{i,j})$ such that w is a substructure of w in the sense of Definition 8. Further, note that (ii) for all $\mathcal {A}_{i,j}\in \mathbf {A}$, all $\phi \in Th(\mathcal {A}_{i,j})$ and all $w \in W(\mathcal {A}_{i,j})$, w⊨ϕ. Moreover, (iii) for any two structures x and x ^′, if x⊨ϕ and S u b(x,x ^′), then x ^′⊨ϕ. (i), (ii) and (iii) imply that w⊨ϕ for all $\phi \in \bigcup _{\mathcal {A}_{i,j} \in \mathbf {A}} Th(\mathcal {A}_{i,j})$. Hence, $Mod(\bigcup _{\mathcal {A}_{i,j} \in \mathbf {A}}Th(\mathcal {A}_{i,j}) )\neq \emptyset$.

Backward: suppose $Mod(\bigcup _{\mathcal {A}_{i,j} \in \mathbf {A}} Th(\mathcal {A}_{i,j})) \neq \emptyset$. Hence, there is a structure $\mathbf {w}=\langle D, \mathfrak {a} \rangle$ such that, for all $\phi \in Th(\mathcal {A}_{i,j})$, w⊨ϕ. We need to construct a consistent choice set of $\mathbf {W} = \{W(\mathcal {A}_{i,j})\; |\; \mathcal {A}_{i,j} \in \mathbf {A}\}$. For any $\mathcal {A}_{i,j}=\langle A_{i,j}, \mathfrak {a}_{i,j} \rangle \in \mathbf {A}$, we define a local world w _i,j by (a) D o m(w _i,j ) = A _i,j and (b) $(R_{k})_{w_{i,j}}=(R_{k})_{\mathbf {w}}\cap A_{i,j}^{n}$, for any n-ary relation symbol R _k that is partially interpreted by $\mathcal {A}_{i,j}$. By the definition of $Th(\mathcal {A}_{i,j})$, any w _i,j thus constructed is a model of α _i,j and an extension of $\mathcal {A}_{i,j}$. Hence, (i) any local world w _i,j thus constructed is a member of $W(\mathcal {A}_{i,j})$. Let W _c be the union of the local worlds w _i,j defined by the above condition (a) and (b). Since all local worlds w ∈ W _c are substructures of w, (ii) any two local worlds w,w ^′∈ W _c must be consistent with one another. (i) and (ii) implies that W _c is a consistent choice set of $\mathbf {W} = \{W(\mathcal {A}_{i,j})\; |\; \mathcal {A}_{i,j} \in \mathbf {A}\}$. This concludes the proof of the sublemma.

Now we are in a position to prove Lemma 1. Forward: suppose A is inconsistent. By Sublemma 1, $Mod(\bigcup _{\mathcal {A}_{i,j}\in \mathbf {A}} Th(\mathcal {A}_{i,j}))= \emptyset$. By the completeness of first-order logic, $\bigcup _{\mathcal {A}_{i,j}\in \mathbf {A}} Th(\mathcal {A}_{i,j})$ is syntactically inconsistent. Hence, there is ϕ such that $\bigcup _{\mathcal {A}_{i,j}\in \mathbf {A}} Th(\mathcal {A}_{i,j}) \vdash \phi$ and $\bigcup _{\mathcal {A}_{i,j}\in \mathbf {A}} Th(\mathcal {A}_{i,j}) \vdash \neg \phi$. (⊩ designates the relation of derivability in classical logic). By compactness of first-order logic, (i) there is a finite set $Th^{\prime }\subseteq \bigcup _{\mathcal {A}_{i,j}\in \mathbf {A}} Th(\mathcal {A}_{i,j})$ such that T h ^′⊩ ϕ and T h ^′⊩¬ϕ. Because T h ^′ is finite, (ii) there is a finite set A ^′such that $Th^{\prime } \subseteq \bigcup _{\mathcal {A}_{i,j}\in \mathbf {A}^{\prime }} Th(\mathcal {A}_{i,j})$. By monotonicity of first-order logic, (i) and (ii) imply that $\bigcup _{\mathcal {A}_{i,j}\in \mathbf {A}^{\prime }} Th(\mathcal {A}_{i,j})$ is classically inconsistent. By Sublemma 1, we can infer therefrom that A ^′ is inconsistent.

Backward: suppose there is finite subset A ^′ ⊆ A that is inconsistent. By Definitions 16 and 17, we can infer therefrom that A is inconsistent. This concludes the proof of Lemma 1.

We can now move on to proving Proposition 1. Suppose w is a global world of L(V ), i.e., an L(V ) interpretation. This world uniquely determines a set A of applications $\mathcal {A}_{i,j}$ by the equation A = A p p(w) (where A p p(w) is defined by Eq. 9). By the definition of A, A is a consistent set of applications in the sense of Definition 16. Suppose, furthermore, that A is maximally consistent in the sense of Definition 18. Then, w is < _s -minimal in the set of L(V )interpretations, and we are done.

If A is not a maximally consistent set of applications, we need to show that it has a maximally consistent superset A ^sof applications. We can achieve this using Zorn’s lemma: if S is a partially ordered set such that every chain in S has an upper bound in S, then S contains a maximal element.

Let $\mathfrak {A}$ be the set of all consistent sets A ^′of applications $\mathcal {A}_{i,j}$ such that A ⊆A ^′. Clearly, the relation ⊆partially orders this set. To make use of Zorn’s lemma, we need to show that any ⊆ sequence 〈A _m 〉 _m∈M of members of $\mathfrak {A}$ (where M is an index set and A _m ⊆A _k for all ordinals m,k ∈ M iff m < k) has an upper bound in $\mathfrak {A}$. M may have finite, countable, or uncountable cardinality. Let $\mathbf {A}^{M}= \bigcup _{m \in M} \mathbf {A}_{m}$. Clearly, (i) for any m ∈ M, A _m ⊆A ^M. Suppose, for contradiction, that A ^Mis inconsistent. By Lemma 1, this implies that there is a finite set $\{\mathcal {A}_{1}, \ldots , \mathcal {A}_{n}\}=\mathbf {A}^{\prime }$ of applications such that A ^′ is inconsistent and A ^′⊆A ^M. Hence, there is an m such that m ∈ M such that $\{\mathcal {A}_{1}, \ldots , \mathcal {A}_{n}\} \subseteq \mathbf {A}_{m}$. Since $\{\mathcal {A}_{1}, \ldots , \mathcal {A}_{n}\}$ is inconsistent, A _m must be so. This is a contradiction since, by assumption, any ⊆ sequence 〈A _m 〉 _m∈M contains only members of $\mathfrak {A}$, the set of consistent sets of applications. Hence, (ii) $\mathbf {A}^{M} \in \mathcal {A}$. (i) and (ii) imply that the sequence 〈A _m 〉 _m∈M has an upper bound in $\mathcal {A}$.

We have thus shown that the conditions of Zorn’s lemma are satisfied for ⊆ chains in the set $\mathfrak {A}$ of consistent sets of applications. Using this lemma, we can infer that A has a superset A ^sthat is maximally consistent. By Definitions 9, 16, 17, and 18, this implies that there is a < _s -minimal world w ^′ such that A p p(w ^′) = A ^s. Using A = A p p(w) and A ⊂A ^s, we can infer therefrom that w ^′< _s w. We have thus shown that for a given L(V )interpretation w, w is < _s -minimal, or there is an L(V )interpretation w ^′such that w ^′ is < _s -minimal and w ^′< _s w. This concludes the proof of Proposition 1.²¹

Proposition 2

LetΘbe a prioritised set of axioms upon which $<^{\Theta }_{s}$ is defined by Definition 14. $<^{\Theta }_{s}$ is smooth in the set of L(V )interpretations.

The proof of this proposition can be obtained by two minor modifications of the proof of Proposition 1. First, in place of the notion of a maximally consistent set of applications, we need to use the notion of a prioritised maximally consistent set of applications:

Definition 19

Prioritised maximally consistent set of applications. LetΘ = 〈T ₁,…,T _m 〉be a prioritisedaxiomatic theory. A set A of applications $\mathcal {A}_{i,j}$is a prioritised maximally consistent set of application iff

• (1) the set $\mathbf {W} = \{W(\mathcal {A}_{i,j})\; |\; \mathcal {A}_{i,j} \in \mathbf {A}$}has a consistent choice set of local worlds

• (2) there is no consistent set A ^′of applications for which there is a levelp (1 ≤ p ≤ m)such that (i) $\mathbf {A} \cap \{\mathcal {A}_{i,j} \;|\; \alpha _{i} \in T_{p} \} \subset \mathbf {A}^{\prime } \cap \{\mathcal {A}_{i,j} \;|\; \alpha _{i} \in T_{p} \}$and (ii) for all levels h < p (h ≥ 1),$\mathbf {A} \cap \{\mathcal {A}_{i,j} \;|\; \alpha _{i} \in T_{h} \} = \mathbf {A}^{\prime } \cap \{\mathcal {A}_{i,j} \;|\; \alpha _{i} \in T_{h} \}$.

Second, in order to justify using Zorn’s lemma, we need to introduce a prioritised variant of the subset relationship between sets of applications. Such a relation can be defined as follows:

Definition 20

⊂ _p .LetΘ = 〈T ₁,…,T _m 〉be a prioritisedaxiomatic theory, and A and A ^′be two consistentsets of applications. A⊂ _p A ^′iff

• (1) there is a level l (1 ≤ l ≤ m)such that $\mathbf {A} \cap \{\mathcal {A}_{i,j} \;|\; \alpha _{i} \in T_{l} \} \subset \mathbf {A}^{\prime } \cap \{\mathcal {A}_{i,j} \;|\; \alpha _{i} \in T_{l} \}$

• (2) for all levels h < l (h ≥ 1),$\mathbf {A} \cap \{\mathcal {A}_{i,j} \;|\; \alpha _{i} \in T_{h} \} = \mathbf {A}^{\prime } \cap \{\mathcal {A}_{i,j} \;|\; \alpha _{i} \in T_{h} \}$.

Definition 21

⊆ _p .A⊆ _p A ^′iff A⊂ _p A ^′or A = A ^′.

The proof that the relation ⊆ _p is a partial order is trivial. No further modifications of the proof of Proposition 1 are needed in order to show that $<_{s}^{\Theta }$ is smooth in the set of L(V )interpretations.

Proposition 4

The inference relation|∼ _e satisfies Right Weakening, And, Or, Cut, Cautious Monotonicity, and Conditionalisation.

Right Weakening. The proof is straightforward and analogous to that of Theorem 1.

And. Likewise, the proof is straightforward and analogous to that of Theorem 1.

To ease the proofs of Cut, Cautious Monotonicity, Conditionalisation, and Or, let us introduce the following convention:

Definition 22

T-maximal model. For a set T of axioms, a worldw is called T-maximal iff w is < _s -minimalin the set of L(V )interpretations, where < _s is the satisfaction ordering induced by T.

A world that is < _s -minimal for T is called T-maximal because it agrees with a maximal set of applications of the axioms of T.

Cut. Suppose (i) T ∪{α} |∼ _e γ and (ii) T |∼ _e α. By (i), (iii) all T ∪{α}-maximal worlds satisfy γ. By (ii), (iv) all T-maximal worlds satisfy α. We show that (v) all T-maximal worlds are also T ∪{α}-maximal. Let w be a T-maximal world. By (iv), this implies that (vi) w satisfies α. Suppose, for contradiction, w is not T ∪{α}-maximal. In view of (vi), this implies that there is a world w ^′that agrees with strictly more applications of the axioms of T than w (in the sense of Eq. 9). Hence, w is not T-maximal. Contradiction. Thus, we have shown (v). (iii) and (v) imply that all T-maximal worlds satisfy γ. Hence, T|∼ _e γ.

Cautious Monotonicity. Suppose (i) T|∼ _e α and (ii) T|∼ _e γ. We show that (iii) all T ∪{α}-maximal worlds are also T-maximal. Let w be a T ∪{α}-maximal world. Suppose, for contradiction, w is not T-maximal. This implies that (iv) there is a T-maximal world w ^′that agrees with strictly more applications of the axioms of T than w (in the sense of Eq. 9). By (i) we know that any T-maximal world agrees with all applications of α. Together with (iv), this implies that (v) w ^′ agrees with all applications of α. (iv) and (v) imply that w is not T ∪{α}-maximal. Contradiction. Hence, we have established (iii). (ii) and (iii) imply T ∪{α} |∼ _e γ.

Conditionalisation. Suppose (i) T ∪{α} |∼ _e γ. Clearly, any T-maximal world does or does not satisfy all instances of α. Let us first take a look at the set M of T-maximal worlds that agree with all applications of α(in the sense of Eq. 9). As shown in the proof of Cut, these worlds are also T ∪{α}-maximal. Using (i), we can infer therefrom that all worlds of M verify γ. Hence, (ii) all worlds w ∈ M verify α → γ. Now, let us take a look at the set M ^′of T-maximal worlds that do not agree with all applications of α. (iii) These worlds, trivially, verify α → γ. Note that any T-maximal world is a member of M or M ^′. Hence, (ii) and (iii) imply T |∼ _e α → γ.

Or. Suppose (i) T ∪{α} |∼ _e γ and (ii) T ∪{β} |∼ _e γ. We need to show that any T ∪{α ∨ β}-maximal model is T ∪{α}-maximal or T ∪{β}-maximal. Note that – by Definition 6 in Section 4.1 – the instances of α ∨ β have the logical form of an instance of α joined by disjunction with β. Suppose, for contradiction, that (iii) there is a T ∪{α ∨ β}-maximal model w that is neither T ∪{α}-maximal nor T ∪{β}-maximal. Suppose, further, w does not verify β. Since w is not T ∪{α}-maximal, we can infer therefrom that there is w ^′such that w ^′ agrees with strictly more applications of the axioms of T than w (while agreeing with at least as many applications of α as w) or w ^′ agrees with strictly more applications of α than w (while agreeing with at least as many applications of the axioms of T as w does). Since w does not satisfy β, this implies that w is not T ∪{α ∨ β}-maximal. Contradiction. Suppose now w does verify β. Since w is not T ∪{β}-maximal, we can infer therefrom that there is w ^′such that w ^′agrees with strictly more applications of the axioms of T than w, while verifying β. This implies that w is not T ∪{α ∨ β}-maximal. Contradiction. We have thus shown that (iii) implies a contradiction. Hence, (iii) is false. This implies that any T ∪{α ∨ β}-maximal model is T ∪{α}-maximal or T ∪{β}-maximal. Because of this, (i) and (ii) imply that T ∪{α ∨ β} |∼ _e γ.

Proposition 5

The inference relation|∼ _e does not always satisfy Reflexivity, Left Logical Equivalence, Rational Monotonicity, and Monotonicity.

A counterexample to reflexivity is easy to construct. Take T = {∀x P(x)},α = ∀x¬P(x).

As for Left Logical Equivalence, take T = ∅, α = ∀x P(x) ∧¬P(a), β = ¬P(a) ∧∀x P(x). Suppose, further, we have R _k = ∅ for all relations R _k of all partial structures that represent applications of α or β. Let the domain D be given by $\{ (a)_{\mathfrak {a}}, (b)_{\mathfrak {a}}\}$, i.e., two objects that are designated, respectively, by the constants a and b. Then, T ∪{α} |∼ _e P(b), while T ∪{β} |≁ _e P(b). As C n(α) = C n(β), this is a counterexample to Left Logical Equivalence. Note that for the different inferential behaviour of α and β it is crucial that α and β, though logically equivalent, have different instances in the sense of Definition 6. P(a) ∧¬P(b) is an instance of α but not an instance of β. For, β itself is the only instance of β.

Here is a counterexample to Rational Monotonicity.

$$T=\{\forall x Q(x), \forall x (Q(x) \rightarrow \neg S(x)), \forall x\neg Q(x)\} $$

$D=\{(a)_{\mathfrak {a}}\}$. F = ∅, were F is defined by Eq. 10. α = ∀x S(x). γ = ∀x(¬Q(x) ∨¬S(x)). Now, these are the diagrams of the T-maximal models (where a T-maximal model is one that is < _s -minimal on the satisfaction ordering induced by T, as explained above):

$$\begin{array}{@{}rcl@{}} \{ Q(a), \neg S(a)\}\\ \{ \neg Q(a), \neg S(a)\} \\ \{ \neg Q(a), S(a) \}. \end{array} $$

Note that γ is verified by all T-maximal models. Hence, (i) T |∼ _e γ. ¬α, by contrast, is not verified by all T-maximal models. Hence, (ii) T |≁ _e ¬α. Now, let us take a look at the diagrams of the T ∪{α}-maximal models:

$$\begin{array}{@{}rcl@{}} \{ Q(a), \neg S(a)\}\\ \{ Q(a), S(a)\} \\ \{ \neg Q(a), S(a) \}. \end{array} $$

Obviously, γ is not verified by all T ∪{α}-maximal models. Hence, (iii) T ∪{α} |≁ _e γ. (i), (ii), and (iii) together describe a counterexample to Rational Monotonicty.

Monotonicity. The just explained counterexample to Rational Monotonicity is of course also one to Monotonicity.