Modelling the Effect of Vaccination Program and Inter-state Travel in the Spread of COVID-19 in Malaysia

Abstract

A modified version of the SEIR model with the effects of vaccination and inter-state movement is proposed to simulate the spread of COVID-19 in Malaysia. A mathematical analysis of the proposed model was performed to derive the basic reproduction number. To enhance the model’s forecasting capabilities, the model parameters were estimated using the Nelder–Mead simplex method by fitting the model outputs to the observed data. Our results showed a good fit between the model outputs and available data, where the model was then able to perform short-term predictions. In line with the rapid vaccination program, our model predicted that the COVID-19 cases in the country would decrease by the end of August. Furthermore, our findings indicated that relaxing travel restrictions from a highly vaccinated region to a low vaccinated region would result in an epidemic outbreak.

1 Introduction

After more than 2 years, Malaysia continues to combat the Coronavirus Disease 2019 (COVID-19), which was originally identified in late December 2019 in Wuhan, China (Zhu et al. 2020). The World Health Organization (WHO) has declared the COVID-19 pandemic, caused by a novel Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2), a public health emergency (World Health Organization declares novel coronavirus 2019). In January 2020, Malaysia reported its first cases of COVID-19 from Chinese visitors who entered the country via Singapore (Ahmad et al. 2020). Since then, Malaysia has reported over 2 million cumulative COVID-19 cases and over 23,000 fatalities as of September 2021 (Aziz et al. 2020). In response to the alarming rates of spread and severity of COVID-19, the Malaysian government has implemented multiple movement control orders (MCOs), international and interstate travel bans, the mandatory wearing of face masks in public spaces, restrictions on social gatherings and the promotion of good personal hygiene to prevent the spread of this virus among the population (Aziz et al. 2020; Cirrincione et al. 2020; Hashim et al. 2021). In addition, several regions in Malaysia were placed under "lockdowns" which restrict the movement of people in and out of these areas in order to assist health authorities in identifying and isolating individuals infected with COVID-19 (Hashim et al. 2021). Although the lockdowns have been successful in isolating infected individuals, the virus has already spread throughout urban and suburban populations.

Given the novelty and rapid spread of this coronavirus, scientists rushed to develop vaccines to prevent its transmission and reduce the global mortality rate. In an effort to achieve high rates of population immunity, Malaysia launched the National COVID-19 Immunisation Programme (NIP) in February 2021, with the goal of vaccinating 90$\%$ of the Malaysian population. However, the COVID-19 vaccination plan got off to a slow start due to economic, political, and social factors, and with the emergence of new SARS-CoV-2 variants that are potentially causing more damage than previously anticipated, there are concerns that the vaccination plan might not achieve its aims. The sudden increase in COVID-19 patients, coupled with the slow implementation of the national vaccination program and a shortage of vaccine supplies, has caused economic turmoil. Furthermore, rising unemployment due to increased COVID-19 cases has resulted in riots, protests and political demonstrations. In view of the looming crisis, the Malaysian government has no choice but to reopen all major economic sectors including education, tourism, retail, and aviation. To further reduce the burden on the healthcare system and to protect infants, children, and medically compromised individuals who are not fully vaccinated, only immunised individuals are permitted to work, travel, and attend social events. Other non-pharmaceutical measures such as inter-state travel will be gradually lifted to create more income-generating opportunities, particularly in the tourism industry. In order to minimise the socio-economic impact of the COVID-19 pandemic, quantitative justifications are vital to determine whether the lockdown should be lifted or travel restrictions should be gradually eased, especially when the number of cases is still high and many individuals have not yet been fully vaccinated.

To assist local health authorities in predicting the dynamics of disease transmission and potential risk of infection in a population, mathematical simulation and evaluation based on the Susceptible-Exposed-Infectious-Recovered (SEIR) model is a useful approach to complement biological and social research in suggesting appropriate and adequate strategies to mitigate the spread of COVID-19 (Syafruddin and Noorani 2012). In Malaysia, mathematical modelling based on the SEIR model has already been employed to understand the effectiveness of disease control strategies such as fogging, vaccination, and control of breeding sites to reduce dengue infections in Shah Alam, Selangor (Syafruddin and Noorani 2012; Tay et al. 2018a, b). Since the beginning of the COVID-19 pandemic, the SEIR model has been widely used to forecast the impact of mass gathering and the success of implementing control measures such as MCO, isolation, and quarantine on the COVID-19 transmission rate in Malaysia (Dass et al. 2021; Gill et al. 2020; Salman et al. 2021). Wong et al. (2021) recently utilised the Susceptible-Infected-Removed (SIR) model to predict the effectiveness of vaccination programs in reducing the SARS-CoV-2 infection rates in Kuala Lumpur, Penang, Sabah, and Sarawak. Since the Malaysian government is considering allowing inter-state travel for fully vaccinated individuals, a projection study should be considered, which combines the implementation of vaccination programs and observation of traffic patterns between different states.

To the best of our knowledge, there is no SEIR model that has been incorporated to predict the impact of vaccination and interstate travel on the spread of COVID-19 in Malaysia. Therefore, in this paper, we modified the classic SEIR model to predict the progression of COVID-19 in Malaysia when the government permits interstate travel for fully-vaccinated individuals. In this study, we employed the data of vaccinated and non-vaccinated people between March 2021 and August 2021. By the time of this study, the percentage of fully vaccinated people was 42$\%$ of the total population as of 9th August 2021. The outcome of this study will highlight the impacts of our vaccination program and consequences of inter-state travel by fully vaccinated individuals and hence enabling policymakers to make informed decisions regarding vaccination programs and socioeconomic activities.

2 Material and Methods

In this section, we will first explain the data used in this work and then discuss the development of our modified SEIR model. We will also explain how the fitting procedures were performed. The final subsection is devoted to the derivation of the basic reproduction number.

2.1 Data Source

The COVID-19 vaccination program in Malaysia is currently being implemented in phases from 24th February 2021 with the aim to curb the COVID-19 pandemic by successfully achieving herd immunity. Due to data availability, this project only considers case data for COVID-19 in Selangor and Kuala Lumpur (S &KL), Malaysia from 2nd March to 15th August 2021, extracted from the Crisis Preparedness and Response Centre (CPRC), Ministry of Health (MOH), Malaysia (data is available on GitHub¹). S &KL is chosen because its data is of better quality compared to those in other states (rural areas), it has the highest COVID-19 recorded cases, and as has more economic activities in Malaysia. The data was used to estimate some model parameters; namely, transmission and death rates. The daily vaccination rate in the state was extracted from the MOH’s official github. The values of other parameters used in the model were obtained from previous studies (see Table 1).

2.2 An Extended SEIR Model

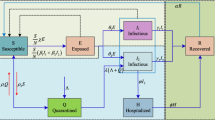
We consider an extended SEIR epidemic disease model by taking into account the effect of the vaccination program and inter-state travel. This has not been considered in other existing literature. Aside from the basic SEIR (Susceptible (S), Exposed (E), Infected (I), and Recovered (R)) compartments, this model includes additional 5 compartments; namely death due to disease (D), people who received only the first dose ($V_1$), fully vaccinated with the second dose ($V_2$), exposed human population who have been vaccinated ($E_V$), and infected human population who have been vaccinated ($I_V$). The dynamical transmission in the human population with vaccination is sketched in Fig. 1. In our model, we consider the following assumptions;

• (i) We assume that, initially, the entire population in S &KL was susceptible. In order for the process to start, there should be at least one exposed or one infectious individual.

• (ii) Only fully vaccinated people are allowed to travel to other states.

• (iii) Like with other vaccines, vaccine breakthrough cases will still happen, even though the vaccines are working as expected. Vaccinated people have a lesser risk of infection, hospitalisation, and mortality than unvaccinated people.

Fig. 1

Disease transmission flow of the extended SEIR model

The model is governed by the following set of nonlinear ordinary differential equations,

$$\begin{aligned} \begin{aligned} \frac{dS}{dt}&= - \frac{\beta (t) S}{N} \left( I + I_v \right) - v_1(t)S + b - \rho S , \\ \frac{dV_1}{dt}&= v_1 (t) S - \frac{\beta (t) (1 - \alpha _1) V_1}{N} ( I + I_v ) -v_2(t)V_1 -\rho V_1,\\ \frac{dV_2}{dt}&= -\frac{\beta (t)(1-\alpha _2)V_2}{N} (I + I_v) + v_2(t)V_1 - \rho V_2 - V_2 \sum _{i=1}^{m-1} \tau _i + \sum _{i=1}^{m-1} \sigma _i V_{2,i},\\ \frac{dE_v}{dt}&= \frac{\beta (t) (1-\alpha _1)V_1}{N} (I_v + I) + \frac{\beta (t)(1-\alpha _2) V_2 }{N} (I_v + I) - \gamma ^{-1} E_v - \rho E_v,\\ \frac{dE}{dt}&= \frac{\beta (t) S}{N} (I + I_v) - \gamma ^{-1} E - \rho E, \\ \frac{dI}{dt}&= \gamma ^{-1} E -( r^{-1} + \mu _1 )I,\\ \frac{dI_v}{dt}&= \gamma ^{-1} E_v - (r^{-1} + \mu _2 )I_v, \\ \frac{dR}{dt}&= r^{-1} (I + I_v)-\rho R, \\ \frac{dD}{dt}&= \mu _1 I + \mu _2 I_v , \end{aligned} \end{aligned}$$

(1)

where N is the size of the population in S &KL. $\beta (t)$ is the transmission rate and $\frac{\beta (t) S}{N} \left( I + I_v \right)$ describes the force of infection for susceptible individual S when making contact with either I or $I_v$. Similarly, the partial ($V_1$) and fully ($V_2$) vaccinated individuals interact with I and $I_v$, then the infection force is represented by $\frac{\beta (t)(1-\alpha _1)V_1(I + I_v)}{N}$ and $\frac{\beta (t)(1-\alpha _2)V_2(I + I_v)}{N}$, respectively. b and $\rho$ are the natural birth number and death rate, respectively. Notice that in our model equation for I and $I_v$, the natural death is not included, since we assume that the infected person may either recover or die due to the disease. $\mu _{1}$ and $\mu _{2}$ are the disease-related death rates of vaccinated and non-vaccinated people, respectively. We assume that fully vaccinated people have 50$\%$ lower death rate compared to partial vaccinated people. $\gamma$ is the disease incubation period and r is the recovery period of the infected people.

$v_{1}(t)$ and $v_{2}(t)$ are the vaccination rates of first and second doses, respectively. The effect of the vaccination is incorporated into our model by the presence of the efficacy coefficients $\alpha _1$ (first dose) and $\alpha _2$ (second dose). If the values are one, the vaccine offers 100$\%$ protection against the virus. $V_{2,i}$ represents the number of vaccinated individuals in the ith state $(i=1,\ldots ,m-1)$, where m is the number of states in Malaysia. The inter-state travel is described by $V_2 \sum _{i=1}^{m-1} \tau _i + \sum _{i=1}^{m-1} \sigma _i V_{2,i}$, where the first term corresponds to the outflow number of fully vaccinated people in S &KL to other states and the second term corresponds to the inflow number of fully vaccinated people in other states. $V_{2,i}$ represents the number of vaccinated individuals in the ith state $(i=1,\ldots ,m-1)$, where m is the number of states in Malaysia. $\tau$ (outflow) and $\sigma$ (inflow) are the number of fully vaccinated people travel into and out of S &KL, respectively. We summarize the list of parameters and their values in Table 1.

Finally, MATLAB R2020b with 64-bit Intel processor was used to perform all the numerical simulations. Each variable in the model was integrated in time with a relative tolerance of $10^{-6}$ employing MATLAB ode15s solver. ode15s is an adaptive multistep solver based on the numerical differentiation formulas of orders 1 to 5. According to Hairer and Wanner (1991), the method has stability regions on the negative real axis but not the whole left half-plane.

Table 1 Parameters description and their corresponding values used in the model simulation. DOSM stands for Department of Statistics Malaysia

2.3 Model Parameterization

The COVID-19 death rate and transmission rate were determined from the model fit data from 2nd March to 9th August 2021. Transmission rate depends on many factors, including measures implemented by the state and the behaviour of the population. Hence, this parameter is uncertain and varies with time. A common approach is to consider a partition into discrete periods, [$t_1$, $t_2$), [$t_2$, $t_3$), ..., [$t_{n-1}$, $t_{n}$], guided by the control measures taken (Carcione et al. 2020). Equivalently, the $\beta$ and $\mu _1$ functions can be expressed in the following form,

$$\begin{aligned} {{\mathcal {Z}}}(t) = H(t_1-t)\cdot z_1 + \sum _{i=2}^{n-1}H(t-t_{i-1})\cdot H(t_i-t)\cdot z_i + H(t-t_n)\cdot z_n. \end{aligned}$$

(2)

where ${{\mathcal {Z}}}=[\beta ,\, \mu _1]$ and $H(\cdot )$ is the Heaviside function. $z_i = [b_i,\, m_i]$ is the estimated transmission and death rates in each period $[t_i, t_{i+1}]$ and $i=1,...,n$ is the number of discrete periods involved. In this study, the period was set to 30 days. Note that $\mu _2 = f(\mu _1)$ where f is defined as in Table 1 . $b_i$ and $m_i$ were estimated using the simplex method by comparing the model output, $y_{\text {sim}}$ to the observed data, $y_{\text {obs}}$ using a residual (also known as ‘error’) function of the form,

$$\begin{aligned} {\mathcal {E}}(t) = \sum _{k=1}^2 \sum _{i=1}^n (y_{\text {sim}}(t_i) - y_{\text {obs}}(t_i))^2. \end{aligned}$$

(3)

$k=1,2$ refers to the number of observed data used to estimate the parameter values, where in our case are the total number of deaths and daily infected cases. In order to accomplish the fit, we used the bounded Nelder-Mead simplex algorithm (Nelder and Mead 1965) and the MATLAB codes were adapted from Aziz and Simitev (2021a, b). The MATLAB codes to perform the optimization procedures can be downloaded from Aziz (2022). The fit was based on the $L^2$-norm and yielded $b_i$ and $m_i$ from the beginning of the epidemic (day 1, March 2nd) to date (day 161, August 9th). Parameters were estimated such that the residual (3) was minimized.

3 Mathematical Analysis of the Model

In this section, we discuss the non-negativity, boundedness, and disease-free equilibrium point of the model.

3.1 Non-negativity of the Model

Theorem 1

If $S_0\ge 0,\, E_0\ge 0,\,I_0\ge 0,\,R_0\ge 0,\,D_0\ge 0,\,(V_1)_0\ge 0,\,(V_2)_0\ge 0,\,(E_v)_0\ge 0,\,(I_v)_0\ge 0$, then all the solutions in system (1) have non-negative values for all $t>0$.

Proof

Because of invariant non-negativity assumption for all $t>0$, the rate of change for each compartment should be at leasr greater than its death rate. From first equation of system (1), we have

$$\begin{aligned} \begin{aligned} \frac{dS}{dt} \ge -\rho S \end{aligned} \end{aligned}$$

(4)

and this implies $S(t) \ge S_0 e^{-\rho S} \ge 0$. Hence, S(t) remains non-negative for all $t>0$. $V_1(t)$, $V_2(t)$, E(t), $E_v(t)$ and R(t) follows similar manner of derivation and one can show that these variables are positive for all $t>0$. For I(t), we have

$$\begin{aligned} \begin{aligned} \frac{dI}{dt}&\ge -(r^{-1} +\mu _1 )I \end{aligned} \end{aligned}$$

(5)

Integrating the equation, we get $I(t) \ge I_0 e^{-(r^{-1} +\mu _1 )I} \ge 0$. One can do the same for $I_v(t)$ and shows that it is non-negative. Therefore, all the variables remain non-negative for all $t\ge 0$. $\square$

3.2 Boundedness

Theorem 2

All solutions of the proposed model with positive initial conditions are bounded and $N(t) \le b/\rho$ for all $t\ge 0$.

Proof

Summing up all the equations in the system (1), the growth rate of the total population can be written as

$$\begin{aligned} \begin{aligned} \frac{dN}{dt} = \frac{dS}{dt} + \frac{dE}{dt} + \frac{dI}{dt} + \frac{dR}{dt} + \frac{dD}{dt} + \frac{dV_1}{dt} + \frac{dV_2}{dt} + \frac{dE_v}{dt} + \frac{dI_v}{dt}. \end{aligned} \end{aligned}$$

(6)

This yields

$$\begin{aligned} \begin{aligned} \frac{dN}{dt} = b - \rho (N - I - I_v) . \end{aligned} \end{aligned}$$

(7)

Since $I(t_{\dagger })=I_v(t_{\dagger }) = 0$ when $t_{\dagger }$ is sufficiently large, then we can reduce the equation to

$$\begin{aligned} \begin{aligned} \frac{dN}{dt} = b - \rho N \end{aligned} \end{aligned}$$

(8)

Upon solving equation (8) and taking the limit of $t \rightarrow \infty$, we get

$$\begin{aligned} \begin{aligned} N(t) \le \frac{b}{\rho }. \end{aligned} \end{aligned}$$

(9)

Thus, together with non-negativity property, we find that

$$\begin{aligned} \begin{aligned} 0\le N(t) \le \frac{b}{\rho }. \end{aligned} \end{aligned}$$

(10)

Therefore, all the variables are bounded. $\square$

3.3 Disease Free Equilibrium

The disease-free equilibrium ${{\textbf {X}}}^0$ of the transmission model is acquired by setting all the derivatives to zero and the infected number to zero. Also, assume that at the beginning of the outbreak all individuals in the population are susceptible, $S/N=1$, that gives us,

$$\begin{aligned} {{\textbf {X}}}^0 = \Bigg (\frac{b}{\rho -v_1},0,0,0,0,\frac{v_1b}{(v_2+\rho )(\rho -v_1)},\frac{v_1v_2b}{\rho (v_2+\rho )(\rho -v_1)},0,0\Bigg ). \end{aligned}$$

(11)

where ${{\textbf {X}}}=(S,E,I,R,D,V_1,V_2,E_v,I_v)$. Next, we derive the basic reproduction number, $R_0$, which is the average number of secondary cases produced by one infected individual introduced into a population of susceptible individuals (van den Driessche 2017). $R_0$ is derived using the next-generation matrix method introduced by van den Driessche (2017). Firstly, we let ${{\textbf {X}}}=(E,E_V,I,I_V)^T$. System (1) then can be written as

$$\begin{aligned} {{\textbf {X}}}' = \mathbb {K}({{\textbf {X}}}) - \mathbb {W}({{\textbf {X}}}), \end{aligned}$$

(12)

where

$$\begin{aligned} \mathbb {K}({{\textbf {X}}})&= \begin{pmatrix} \frac{\beta S(I+I_v)}{N} \\ \frac{\beta (1-\alpha _1)V_1(I_v + I)}{N} + \frac{\beta (1-\alpha _2) V_2 (I_v + I)}{N} \\ \gamma ^{-1}E \\ \gamma ^{-1}E_v \end{pmatrix} \end{aligned}$$

(13)

and

$$\begin{aligned} \mathbb {W}({{\textbf {X}}})&= \begin{pmatrix} (\gamma ^{-1}+\rho )E \\ (\gamma ^{-1}+\rho )E_v \\ (r^{-1}+\mu _1)I \\ (r^{-1}+\mu _2)I_v \end{pmatrix} \end{aligned}$$

(14)

Their corresponding Jacobian matrices at the disease-free equilibrium are

$$\begin{aligned} J_{{\mathbb {K}}}= & {} \begin{pmatrix} 0 &{} 0 &{} \frac{\beta S^0}{N} &{} \frac{\beta S^0}{N} \\ 0 &{} 0 &{} \frac{\beta (1-\alpha _1)V_1}{N} + \frac{\beta (1-\alpha _2) V_2}{N} &{} \frac{\beta (1-\alpha _1)V_1}{N} + \frac{\beta (1-\alpha _2) V_2}{N} \\ \gamma ^{-1} &{} 0 &{} 0 &{} 0 \\ 0 &{} \gamma ^{-1} &{} 0 &{} 0 \end{pmatrix} \\ J_{{\mathbb {W}}}= & {} \begin{pmatrix} \gamma ^{-1}+\rho &{} 0 &{} 0 &{} 0 \\ 0 &{} \gamma ^{-1}+\rho &{} 0 &{} 0 \\ 0 &{} 0 &{} r^{-1}+\mu _1 &{} 0 \\ 0 &{} 0 &{} 0 &{} r^{-1}+\mu _2 \end{pmatrix} \end{aligned}$$

Following the method described in van den Driessche (2017), the basic reproduction number, $R_0$ is described by the largest eigenvalue of the next-generation matrix $J_{\mathbb {K}}J_{\mathbb {W}}^{-1}$. This yields

$$\begin{aligned} R_0 = \sqrt{\frac{\beta \gamma ^{-1} \big [S^0g_2 +V_1^0 g_1(1-\alpha _1)+V_2^0(g_2-\alpha _2g_1 ) \big ]}{Ng_1g_2(\gamma ^{-1}+\rho )} }, \end{aligned}$$

(15)

where $g_1 = \mu _1+r^{-1}$ and $g_2 = \mu _2+r^{-1}$. $S^0, V_1^0, V_2^0$ are as defined in (11). $R_0$ is used to measure the severeness of the disease epidemic. A disease outbreak is expected to occur if $R_0>1$ and contain if $R_0<1$ (Carcione et al. 2020; van den Driessche 2017).

Next we want to determine the local stability of (11). System (1) can be simplified into a reduced form by eliminating the last equation for the death compartment (D). This is because the compartment has no significance effect on the whole system and it can also be determined from $D=N-\sum {\textbf{X}}$ where ${\textbf{X}}$ is the other compartments in the system. The Jacobian matrix of the reduced model at the disease-free equilibrium is described as

$$\begin{aligned} J({{\textbf{X}}^0}) = \begin{pmatrix} -v_1-\rho &{} 0 &{} -\frac{\beta S^0}{N} &{} 0 &{}0 &{}0 &{}0 &{}-\frac{\beta S^0}{N} \\ 0 &{} -\gamma ^{-1}-\rho &{} \frac{\beta S^0}{N} &{} 0 &{}0 &{}0 &{}0 &{}\frac{\beta S^0}{N} \\ 0 &{} -\gamma ^{-1} &{} -r^{-1}-\mu _1 &{}0 &{}0 &{}0 &{}0 &{}0 \\ 0 &{} 0 &{} r^{-1} &{}-\rho &{}0 &{}0 &{}0 &{}r^{-1}\\ v_1 &{}0 &{}\epsilon _1 &{}0 &{}-v_2-\rho &{}0 &{}0 &{}\epsilon _1 \\ 0 &{}0 &{}\epsilon _2 &{}0 &{}v_2 &{}-\rho &{}0 &{}\epsilon _2 \\ 0 &{}0 &{}\epsilon _3 &{}0 &{}0 &{}0 &{}-\gamma ^{-1}-\rho &{}\epsilon _3 \\ 0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}\gamma ^{-1} &{}-r^{-1}-\mu _2 \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \epsilon _1&= -\frac{\beta (1-\alpha _1) V_1^0}{N}, \\ \epsilon _2&= -\frac{\beta (1-\alpha _2) V_2^0}{N}, \\ \epsilon _3&= \frac{\beta (1-\alpha _1) V_1^0}{N}+\frac{\beta (1-\alpha _2) V_2^0}{N}. \end{aligned} \end{aligned}$$

By using MATLAB symbolic math toolbox, we find that the disease-free equilibrium ${\textbf{X}}^0$ is locally stable when $R_0<1$ and locally unstable when $R_0>1$. See supplementary material for a more detailed discussion.

4 Results

All the significant results obtained from our model are presented in this section. This section consists of three subsections. In the first subsection, we performed a simple simulation to simulate the COVID-19 outbreak. The second subsection will focus on sensitivity analysis, where we vary some of the parameters in the model and then observe the outcomes. The aim was to perform simulations of various possible cases, which cannot be done in a real situation. Finally, we present the results of our optimization procedures in the last subsection.

4.1 Outbreak Simulation of COVID-19

To begin with, we simulate the outbreak by considering a set of base parameters as listed in Table 1. The travelling rates are set to 0 to indicate that the border between regions is closed. At time, $t=0$, we set $E(0)=1000$ and other variables are zero, except for $S(0)=N - \sum {{\textbf {y}}}(0)$, where ${{\textbf {y}}}$ is a vector containing all other variables.

Fig. 2

Simulation of COVID-19. a Number of infected cases for vaccinated and non-vaccinated groups, b Total cumulative deaths, c Number of first and second doses administered, d Other model outputs. E(0) = 1000. $\beta = 0.18$, $\mu _1 = 0.014$ and the other parameter values are as listed in Table 1. violet star marker corresponds to $I(t)=I_v(t)$

Figure 2a, b shows the number of infected cases and total cumulative confirmed deaths due to disease for both vaccinated and non-vaccinated individuals, respectively. As can be seen, the non-vaccinated people are affected the most, with a maximum number of nearly 2500 infected cases and approximately 3400 deaths in total. With large numbers of people being vaccinated (see Fig. 2c), the number of infected cases among non-vaccinated people exhibits an immediate fall after day 100. It is interesting to note that the number of infected cases among the vaccinated people shows a slight increase approximately from day 100, reaching a peak on day 138 with a maximum number of nearly 400 cases. This is expected as the population is now dominated by vaccinated people. While vaccines are known to be effective at preventing infection, a small proportion of fully vaccinated individuals will still catch the disease. The peak of infected cases for the vaccinated group, however, is approximately 6 times lower than the peak of cases for the unvaccinated group. This is illustrated in Fig. 2a. It shows that vaccines can protect people from being infected.

On day 170, we observe a comparable number of infected cases ($\approx$185 cases) recorded in both groups, marked as a violet star marker in Fig. 2a. Although the number of cases is equivalent, the number of deaths that occurred among the vaccinated group on that day is twice the size of the other group. The results demonstrate that the risk of death is vastly lower for those who have been vaccinated against COVID-19, compared to those who have received no vaccine doses. Finally, Fig. 2d shows the number of individuals in different classes generated from this simulation.

4.2 Sensitivity Analysis

Hereafter, we perform a local sensitivity analysis on the model and observe how the model responds when some of the key parameters are changed. By varying the model parameters, a scenario analysis is performed to give insight into the influence of the system parameters on the selection of strategies, thus enabling more informed decisions.

Impact of vaccination We first investigate the effect of vaccine-related parameters and variables in the model on the spread of the disease. Particularly, they are vaccination rates $v_1, v_2$, vaccine efficacy $\alpha _1$, and initial proportion of fully vaccinated people $V_2(0)$. In order for the outbreak to occur, there should be at least one exposed or infectious individual. Hence, we assume that there are 1000 people who have been exposed to the disease initially. We also assume that the vaccines offer 70$\%$ and 80$\%$ protection against COVID-19 after the first and second doses, respectively. We start our numerical simulation for a period of 5 months with and without vaccination. The total number of vaccine doses administered per day is varied between 0 and 90,000, and the effects on the number of infected cases and total deaths are observed.

Numerical results are presented in Fig. 3. Overall, we can see that intensifying the vaccination campaign starts to significantly decrease the number of infected cases and deaths in the population. In particular, when no vaccine is available, the peak of infected cases may rise to 2644. Meanwhile, when 50,000 doses of vaccines are administered per day, the peak has been reduced to 1496. This represents a 43 percent reduction. The peak gets lower as more vaccines are rolled out, as depicted in Fig. 3a. On the other hand, it is interesting to highlight that the vaccination programme has significantly reduced the total number of deaths due to the disease (Fig. 3b). In comparison to a no vaccination condition, 100,000 doses of vaccine per day can save approximately 3000 lives. While this number is just an estimation, one should notice that vaccines can reduce the risk of death by at least 50$\%$.

Fig. 3

Effects of vaccination rates. a Number of infected cases and b total cumulative deaths for different values of vaccination rates. $E(0)=E_v(0)=500$ and other parameters are kept constant as listed in the Table 1

Fig. 4

a Number of infected cases and b total cumulative deaths for different initial proportion of fully vaccinated people ($V_2(0)$) in the region. $E(0)=E_v(0)=500$ and other parameters are kept constant as listed in Table 1

Fig. 5

a The number of infected cases and b total cumulative deaths for various values of vaccine efficacy of first dose, $\alpha _1$. $E(0)=E_v(0)=500, V_1(0)=V_2(0)=0.1 \times N$, where N is the size of population as stated in Table 1. Other parameters are kept constant

Next, we investigate the effects of having various proportions of fully vaccinated individuals ($V_2(0)$) in the group. In this simulation, we vary the proportion value from 0 to 70$\%$, as indicated in Fig. 4a. The results of the simulation show a decrement in the peak of infected cases, starting from 1000 cases (none is vaccinated at the beginning) to as low as 473 cases (70$\%$ of the total population is vaccinated). The number of infected cases also exponentially decays faster as $V_2(0)$ increases. A similar pattern is exhibited in the cumulative deaths, where the curves plateau quicker as more people have been vaccinated initially (Fig. 4b). It demonstrates that achieving herd-immunity through vaccination, in which the threshold is between 60 and 70$\%$ of the population, is crucial to stopping the spread of the disease.

Finally, to further appreciate our model in predicting the spread of disease, we observe the effect of vaccine efficacy, $\alpha _1$ on the dynamic of COVID-19 cases and deaths. The results are presented in Fig. 5. As shown in both Fig. 5a and b, the daily reported cases and deaths increase as vaccines become less effective (decrease in the $\alpha _1$ value). While vaccine waning is still possible because of factors such as the emergence of new variants, the results here also give us a prediction for when it happens later.

Impact of inter-state travel Using a similar model, we performed numerical simulations to predict the number of infected cases when fully vaccinated individuals were allowed to travel between two regions (let us denote them as Region A and B). We assume that both regions have an equal population size N but with a different initial proportion of fully vaccinated individuals ($V_2(0)$). Particularly, we consider two different cases, which are,

• I. Mobility from a highly vaccinated region to a low-vaccinated region; $V_{2,A}(0)= 0.7\times N$ and $V_{2,B}(0)=0.2\times N$

• II. Mobility from a highly vaccinated region to a highly vaccinated region; $V_{2,A}(0)= 0.7\times N$ and $V_{2,B}(0)=0.7\times N$

where $V_{2,A}(0)$ and $V_{2,B}(0)$ corresponds to the number of fully vaccinated people in Region A and B, respectively. The vaccination rates and the implementation of control measures in both regions are assumed to be similar and comparable. Since we had no data on the number of people travelling from Region A to Region B, the parameter $\tau$ varied between 10,000 and 30,000 people per day. Also, we assume that people from Region A would stay, on average, five days in Region B. This causes the travel rate from Region B to Region A, $\sigma$ to be lower by a factor of 5. Additional assumptions include that if a person was found to be infected, they were not allowed to travel to avoid disease transmission to another region.

We began our numerical simulation for a period of 150 days with and without inter-state movement. The results of case (I) are shown in Fig. 6a and b. Notice that the number of reported cases in Region A is comparable for all $\tau$. This is, in fact, predictable as at least 70$\%$ of the population in the region has been vaccinated. As these people move to Region B, the interaction with the local community has increased the number of cases in Region B. The peak of infected cases becomes larger (roughly 25$\%$ increment at most) as more people travel (increase in the value of $\tau$) into the region. As the model only allows people in compartment $V_2$ to travel, we expect a more significant impact would be seen if infectious people could freely travel. On the other hand, for the second situation, we observe equivalent results in terms of the number of daily infected cases in both regions when the travelling parameter $\tau$ is varied (Fig. 6c, d). The peak number of cases in Region B is also lower than the first case for all $\tau$. This is in line with the high number of vaccinated people in Region B (case ii), which resulted in a lower peak.

Fig. 6

Effects of inter-state travel. Number of infected cases in Region A and Region B for different values of travelling coefficients. a, b corresponds to the mobility of people from Region A (highly vaccinated; $V_{2,A}(0)=0.7\times N$) to Region B (low vaccinated; $V_{2,B}(0)=0.2\times N$). c, d corresponds to the mobility of people from Region A (highly vaccinated; $V_{2,A}(0)=0.7\times N$) to Region B (highly vaccinated; $V_{2,B}(0)=0.7\times N$). $E_{A,B}(0)=1000$ and other parameters are as listed in the Table 1

4.3 Disease Outbreak in Selangor and Kuala Lumpur (S &KL)

Next, we attempt to model the COVID-19 epidemic in Selangor and Kuala Lumpur (Malaysia), for which data is available at the Crisis Preparedness and Response Centre (CPRC), Ministry of Health, Malaysia. The available data allows us to perform a relatively reliable fit to the observed data from day 1 (March 2nd) to day 161 (August 9th), as shown in Fig. 7. For this simulation, the population in Selangor and Kuala Lumpur (S &KL) is considered as a single population. It is not possible to model for Selangor or Kuala Lumpur separately because people commute within the states frequently.

Fig. 7

The Selangor and Kuala Lumpur cases history. a Daily active cases, b Total cumulative deaths, c Total percentage of fully vaccinated individuals and d Other model outputs. In a–c, model outputs are plotted in solid red line and the observed data is plotted in blue dot. Grey dash-dotted line in a is the estimated transmission rate obtained from the optimization procedures

Figure 7a depicts the results of our model fit with the active cases between the observed time frame. It is estimated that the transmission rate, $\beta$ shows an upward trend from $\beta = 0.0788$ at the beginning ($t_1$ = day 1) to $\beta = 0.2601$ at day 60 (April 30th). On day 92 (June 1st), the Malaysian government imposed the third national lockdown in order to reduce the spread of the disease, which resulted in a decrease in the transmission rate of 0.1176. This is expected since the public was embracing stay-at-home orders, which directly contributed to the reduction of the transmission rate, thereby decreasing the number of active cases (day 96 to 116). However, from the observed data, a rise in the number of daily cases from day 120 onward (June 29th) in Fig. 7a indicates the ineffectiveness of the lockdown. It is debatable whether the Malaysian government applied the same lockdown rules as in the previous lockdown (March 2020).

Based on the estimated parameter values, we performed a short term forecast to predict the spread of the disease ahead. We extended the simulation time period for 30 days starting on August 9th and then plotted the number of infected cases. Note that long-term prediction is not suitable using the model as the situation may change as time goes on, requiring an update to the model. Our model predicts a decrease in the number of COVID-19 cases from late August. This is probably due to the increase in the number of vaccinated people (Fig. 7c). At the time of writing (September 7th), the number of daily cases reported from August 9th to September 9th showed a downward trend, which is qualitatively similar to our model’s prediction.

In addition, Fig. 7b depicts the total cumulative confirmed deaths between simulated and real data within the observed period. The model simulation achieves a very good fit to the observed data (blue dots), with an exponential growth in the number of deaths. Also, one can notice that the number of deaths is in line with the number of cases. In other words, the higher the number of cases, the higher the number of deaths. From day 1 to approximately day 60 (April 30th), the data shows a slight increase in the total confirmed deaths and begins to gradually increase after that as many active cases are reported.

Figure 7c shows the total percentage of fully vaccinated people in S &KL for both simulated and real data. As can be seen, the total cumulative population that received the second dose of vaccine is approximately $30\%$ on August 15th. Our prediction is not far enough from real data, where the number of fully vaccinated people has reached at least $40\%$ of the total population in S &KL. The small discrepancy here is due to our assumption that the recovered individuals (R compartment) were not administered vaccines. At this point in our work, we do not have enough data to incorporate this effect into the model; this would require the addition of another coefficient that takes into account the re-population of the vaccinated compartment. Finally, Fig. 7d shows the number of individuals in the different classes within the simulated period.

5 Discussion

The majority of COVID-19 outbreak modelling studies in the literature simulate a forecast of cases occurring during an epidemic without accounting for the effects of vaccination programmes as the vaccine was not available during the time of these studies. This work extends previously proposed SEIR models, which now include the effect of both vaccination and inter-state travel.

The findings from our study showed that the vaccination programme has a significant effect on the spread of the disease. The number of cases exhibited a downward trend as more people were vaccinated (Figs. 3, 4, 5). A rapid vaccination programme and effective vaccines play important roles in eradicating the disease faster. This is consistent with the results reported in Layan et al. (2021). While vaccination has proven to be an effective method of protecting people from the virus, our simulations show that a vaccine breakthrough is still possible. The number of infected cases among vaccinated people, however, is much lower than that of non-vaccinated people (Fig. 2a), indicating the effectiveness of the vaccines in lowering the transmission risk. However, COVID-19 transmission between unvaccinated people is the primary cause of continued spread (CDC. Science brief 2021). It is also important to highlight that the vaccines are so effective in reducing the risk of death for infected individuals by half (Fig. 2b).

In addition, we find that the inter-region movement would cause an outbreak (Fig. 7). In the model, we only allowed fully vaccinated individuals to cross the border, but this still failed to prevent disease spread. The interaction with local infectious people has probably caused the outbreak. We expect that the number of local cases would be higher if the fully vaccinated people were infectious prior to travelling. This effect, however, was not considered in this study. Depending on daily travel rates, the severity of the outbreak could vary as the number changes. Although our study focused on two different populations (regions) only, the model can actually be extended to multiple regions by modifying the background conditions such as population sizes, local transmission rates, and daily travel rates. Results presented by our model have highlighted the impact that would occur if travelling restrictions are lifted improperly. In addition, our model can be a good framework for the authorities to plan a safe travel bubble for the tourism industry, for example.

To validate our model’s prediction capability, we performed the optimization procedures by fitting the model to a set of real data. The observed data was comprised of daily infected cases and total cumulative deaths in Selangor and Kuala Lumpur, in which taken from MOH’s github. Note that the reported daily infected cases cannot be used as the sole quantity for calibration because this data cannot be trusted. This number depends on many factors, including testing capacity and strategy. All countries’ reported confirmed cases underestimate the number of actual infected people. Many asymptomatic and mildly symptomatic people were unlikely to have been diagnosed. Hence, using the number of casualties could improve the forecast due to the fact that this data is more reliable than that of infected cases. In order to accomplish the fit between model outputs and observed data, we used the simplex method (Nelder and Mead 1965), where the MATLAB codes were made available in Aziz (2022).

As shown in Fig. 7a, b, the targeted model outputs exhibited a good fit with the observed data within the selected time period. The model predicts a decrease in COVID-19 cases from late August due to the rapid vaccination program. Interestingly, despite being "locked" down for several months (from June 1st until August 9th), the number of cases was constantly increasing. This suggests that the lockdown measure was not properly implemented. Partially enforcing lockdown would very certainly lead to periodic fluctuations in the number of infection cases (Fig. 2a). Many studies have shown that lockdown is the most effective non-pharmaceutical intervention (Haug et al. 2020; Gill et al. 2020), but it requires strict regulations.

While numerical results are obtained for certain states over a specified time period, the model can be reparameterized for other states and updated when the epidemiological situation changes. We updated the model a number of times by including or removing initial assumptions as our understanding of the nature of disease transmission improved. Since modelling the exact behaviour of the disease is too complicated, our proposed model has some caveats and limitations that need to be considered in future studies. Firstly, we only considered a cumulative factor embedded in a single parameter $\beta$ to describe the transmission rate of the virus. Other non-pharmaceutical interventions, for example, social distancing, practising hand hygiene, use of face masks, and banning of large gatherings, are not separately considered in the model (Chu et al. 2020) because of a lack of empirical data about the efficacy of these individual control measures. Also, adherence to these control measures may be considerably different across regions and over time.

Secondly, the population density in a particular region is not homogeneous in reality, which means we expect a higher infection rate in a dense location. We, however, did not model this effect as it requires the incorporation of a spatial diffusion equation (Noble 1974) or the use of agent-based models (Ying and O’Clery 2021; Frias-Martinez et al. 2011). Thirdly, according to a study conducted by Seow et al. (2020), it was highlighted that levels of antibodies that kill coronavirus waned over the 3-month study; this problem may make it more likely for those who have already recovered from the virus to become infected again (Breathnach et al. 2021). The second infection, however, would likely be milder than the first. Future studies may need to include the effect of multiple infections as well as vaccine waning in the model development as done by Salman et al. (2021).

6 Conclusion

In this study, we proposed an extended SEIR transmission model by incorporating both vaccination programmes and inter-state movement. The model was mathematically analysed to determine the disease-free equilibrium and the basic reproduction number. We then carried out several parameter sensitivity analyses to observe the model outputs in simulating various possible cases. In particular, the effects of vaccination-related parameters were investigated by observing the number of infected cases and deaths as these parameters were modified. Moreover, the model was also used to predict the spread of the virus as inter-state travel was allowed. The outbreak simulation involved the movement of fully vaccinated individuals from a highly dense vaccinated region to a less dense vaccinated region. The results demonstrated the risk of the emergence of another infection wave due to inter-state movement.

To validate the model outputs and estimate the unknown parameters, we performed a parameter estimation method based on the Nelder-Mead simplex method in order to enhance the model’s prediction capability. The real data of active cases and total cumulative deaths showed a good fit to our respective model outputs. Using the estimated parameters from both the fitting process and existing literature, we used the model to perform short-term predictions of the number of infected cases in Selangor and Kuala Lumpur. Our model predicted that the COVID-19 cases would be reduced from late August. Finally, the new proposed model can serve as a tool for health authorities to plan, prepare, and take appropriate interventions and decisions to control the transmission of the disease.