If κ is a measurable cardinal, then it is a well-known fact that there is at least one normal ultrafilter over κ. In [K-1], Kunen showed that one cannot say more without further assumptions, for if U is a normal ultrafilter over κ, then L[U] is an inner model of ZFC in which κ has exactly one normal measure. On the other hand, Kunen and Paris showed [K-P] that if κ is measurable in the ground model, then there is a forcing extension in which κ has 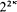normal ultrafilters, so it is consistent that κ has the maximum possible number of normal ultrafilters. Starting with assumptions stronger than measurability, Mitchell [Mi-1] filled in the gap by constructing models of ZFC + GCH satisfying “there are exactly λ normal ultrafilters over κ”, where λ could be κ+ or κ++ (measured in the model), or anything ≤ κ. Whether or not Mitchell's results can be obtained by starting only with a measurable cardinal in the ground model and defining a forcing extension is unknown.

There are substantial differences between the Mitchell models and the Kunen-Paris models. In the Kunen-Paris models κ can be the only measurable cardinal. However, in the Mitchell model in which κ has exactly 2 normal ultrafilters, one of them contains the set {α < κ: α is measurable} while the other does not. Thus it is natural to ask if it is possible to get a model M of ZFC in which κ is the only measurable cardinal and κ has exactly 2 normal ultrafilters. In this paper we will show that, using appropriate large cardinal assumptions, the answer is yes.