Article contents
COMPLEXITY OF COMPLEXITY AND STRINGS WITH MAXIMAL PLAIN AND PREFIX KOLMOGOROV COMPLEXITY
Published online by Cambridge University Press: 25 June 2014
Abstract
Péter Gács showed (Gács 1974) that for every
n there exists a bit string x of length
n whose plain complexity
C(x) has almost maximal conditional complexity
relative to x, i.e., 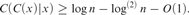 $C\left( {C\left( x \right)|x} \right) \ge {\rm{log}}n - {\rm{log}}^{\left( 2 \right)} n - O\left( 1 \right)$ (Here
$C\left( {C\left( x \right)|x} \right) \ge {\rm{log}}n - {\rm{log}}^{\left( 2 \right)} n - O\left( 1 \right)$ (Here  ${\rm{log}}^{\left( 2 \right)} i = {\rm{loglog}}i$.) Following Elena Kalinina (Kalinina 2011), we provide a simple
game-based proof of this result; modifying her argument, we get a better (and
tight) bound
${\rm{log}}^{\left( 2 \right)} i = {\rm{loglog}}i$.) Following Elena Kalinina (Kalinina 2011), we provide a simple
game-based proof of this result; modifying her argument, we get a better (and
tight) bound 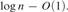 ${\rm{log}}n - O\left( 1 \right)$ We also show the same bound for prefix-free complexity.
${\rm{log}}n - O\left( 1 \right)$ We also show the same bound for prefix-free complexity.
Robert Solovay showed (Solovay 1975) that infinitely many strings
x have maximal plain complexity but not maximal prefix
complexity (among the strings of the same length): for some c
there exist infinitely many x such that 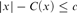 $|x| - C\left( x \right) \le c$ and
$|x| - C\left( x \right) \le c$ and 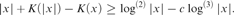 $|x| + K\left( {|x|} \right) - K\left( x \right) \ge {\rm{log}}^{\left( 2 \right)} |x| - c{\rm{log}}^{\left( 3 \right)} |x|$ In fact, the results of Solovay and Gács are closely
related. Using the result above, we provide a short proof for
Solovay’s result. We also generalize it by showing that for some
c and for all n there are strings
x of length n with
$|x| + K\left( {|x|} \right) - K\left( x \right) \ge {\rm{log}}^{\left( 2 \right)} |x| - c{\rm{log}}^{\left( 3 \right)} |x|$ In fact, the results of Solovay and Gács are closely
related. Using the result above, we provide a short proof for
Solovay’s result. We also generalize it by showing that for some
c and for all n there are strings
x of length n with 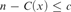 $n - C\left( x \right) \le c$ and
$n - C\left( x \right) \le c$ and 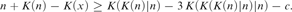 $n + K\left( n \right) - K\left( x \right) \ge K\left( {K\left( n \right)|n} \right) - 3K\left( {K\left( {K\left( n \right)|n} \right)|n} \right) - c.$ We also prove a close upper bound
$n + K\left( n \right) - K\left( x \right) \ge K\left( {K\left( n \right)|n} \right) - 3K\left( {K\left( {K\left( n \right)|n} \right)|n} \right) - c.$ We also prove a close upper bound  $K\left( {K\left( n \right)|n} \right) + O\left( 1 \right)$
$K\left( {K\left( n \right)|n} \right) + O\left( 1 \right)$
Finally, we provide a direct game proof for Joseph Miller’s
generalization (Miller 2006) of the same Solovay’s theorem: if a
co-enumerable set (a set with c.e. complement) contains for every length a
string of this length, then it contains infinitely many strings
x such that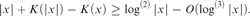 $|x| + K\left( {|x|} \right) - K\left( x \right) \ge {\rm{log}}^{\left( 2 \right)} |x| - O\left( {{\rm{log}}^{\left( 3 \right)} |x|} \right).$
$|x| + K\left( {|x|} \right) - K\left( x \right) \ge {\rm{log}}^{\left( 2 \right)} |x| - O\left( {{\rm{log}}^{\left( 3 \right)} |x|} \right).$
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2014
References
REFERENCES
- 10
- Cited by




