Definition. For ordinals α ≤ κ, = [X]α = {p ⊆ X ∣ ot (p) = α}. For α ≤, κ, κ a cardinal, 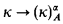holds iff for every partition F: [Κ]κ → A, there is an X ∈ [Κ]κ with F constant on [X]α. X is called homogeneous for F. When A = 2 the subscript is omitted.

It has been known since the sixties that for finite exponents all such properties are equivalent, i.e., κ→ (κ)2 iff 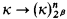for all n < ω, β < κ. The infinite case is much more difficult, though it is not actually known to be different. The usual methods for dealing with partitions fail, and as the weakest of these properties violates the Axiom of Choice, many techniques are unavailable.

It is extremely unlikely that an infinite exponent can be increased, but infinite subscripts are generally possible.

Theorem. If ∥ α ∥ · 2 ≤ α, then κ → (κ)α implies 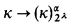for all λ < κ.

In §1, we show the subscript can be any λ < κ. In §2 we extend this to 2λ. In §3 we discuss the possibilities with limited amounts of well-ordered choice, and apply the theorem to the problem of obliging ordinals. Except in §3, we assume no choice. For the story of finite exponents, see [1]. For the relationship between infinite-exponent partition relations and choice, see [4].