Abstract
The traditional Lewis–Stalnaker semantics treats all counterfactuals with an impossible antecedent as trivially or vacuously true. Many have regarded this as a serious defect of the semantics. For intuitively, it seems, counterfactuals with impossible antecedents—counterpossibles—can be non-trivially true and non-trivially false. Whereas the counterpossible "If Hobbes had squared the circle, then the mathematical community at the time would have been surprised" seems true, "If Hobbes had squared the circle, then sick children in the mountains of Afghanistan at the time would have been thrilled" seems false. Many have proposed to extend the Lewis–Stalnaker semantics with impossible worlds to make room for a non-trivial or non-vacuous treatment of counterpossibles. Roughly, on the extended Lewis–Stalnaker semantics, we evaluate a counterfactual of the form "If A had been true, then C would have been true" by going to closest world—whether possible or impossible—in which A is true and check whether C is also true in that world. If the answer is "yes", the counterfactual is true; otherwise it is false. Since there are impossible worlds in which the mathematically impossible happens, there are impossible worlds in which Hobbes manages to square the circle. And intuitively, in the closest such impossible worlds, sick children in the mountains of Afghanistan are not thrilled—they remain sick and unmoved by the mathematical developments in Europe. If so, the counterpossible "If Hobbes had squared the circle, then sick children in the mountains of Afghanistan at the time would have been thrilled" comes out false, as desired. In this paper, I will critically investigate the extended Lewis–Stalnaker semantics for counterpossibles. I will argue that the standard version of the extended semantics, in which impossible worlds correspond to maximal, logically inconsistent entities, fails to give the correct semantic verdicts for many counterpossibles. In light of the negative arguments, I will then outline a new version of the extended Lewis–Stalnaker semantics that can avoid these problems.
Similar content being viewed by others
Notes
Also, I have for simplicity omitted an accessibility relation between worlds in (LS-ConFac).
For further discussion of what a general purpose world-making language may look like, refer to Chalmers (2011) and Lewis (1986), chap. 3. Insofar as one has a better grasp of a class of primitive, arbitrarily fine-grained propositions that can stand in logical relations to each other, it is also worth pointing out that one might replace all talk about sentences with talk of such propositions without affecting the main ideas and arguments in the paper.
Although I will work with a simple logical language that contains only \(\neg\) and ∧ as logical symbols, it will be easy to see that the results in Sect. 3 will continue to hold if we enrich the world-making language to include symbols for the other propositional connectives as well.
See the appendix for the proof of (Satisfiability).
Assuming that general-purpose possible worlds are also mathematically and analytically possible, maximal consistent sets of sentences clearly cannot play this general-purpose role. Yet, since my main focus is on counterlogicals, we can set aside issues about non-logical a priori truths such as those resulting from mathematical and analytic reasoning.
Thanks to an anonymous referee for discussion here.
For further discussion of logically consistent worlds that represent themselves as being logically non-classical in different ways, see Krakauer (2012).
See the appendix for the proof of (Inc).
Strictly, w 1 and w 2 cannot contain just one instance of a LNC-inconsistency, but I simplify the presentation here—as I do below. If need be, we can stipulate that A 1 and B 1 are atomic sentences and that all LNC-inconsistencies in w 1 involve A 1, whereas all LNC-inconsistencies in w 2 involve B 1. Intuitively, on such a picture, if we were to remove all sentences involving A 1 from w 1, and all sentences involving B 1 from w 2, the two worlds would become consistent.
I state (7) to (9) schematically using, for simplicity, expressions from the metalanguage.
Counterlogicals similar to those that caused problems for (M-ConFac) in the second part of the argument above can easily be generated for the kinds of antecedents that I will consider in this section.
It will not help the proponent of (M-ConFac) to expand the world-making language to include symbols ∨ and → that play the same inferential roles as classical disjunction and material implication—and modify (Evaluation) in Sect. 2.1 accordingly. For given the proof of (Inc) in the appendix, it is not hard to see how it generalizes to sentences involving ∨ and →. In turn, it is not hard to verify that arguments similar to those in Sect. 3 involving ∨ and → can be leveled against (M-ConFac). So for now I set aside the option of enriching the world-making language.
The semantics of (P-ConFac) differs slightly from the semantics of (ConFac) because there are now two ways in which a sentence can fail to be true in a world: either if it is false in the world, or if it is indeterminate in the world.
Since classical logic has an explosive consequence relation, every classically inconsistent set will be identical to the set that contains every sentence in the world-making language. This “explosive” set of sentences will not correspond to any logically possible world, and henceforth we should assume that it is excluded from the space of logically possible worlds.
For now I leave it an open question whether we want to quantify over only existing logics, or also over conceivable logics.
In claiming that we can fruitfully utilize certain aspects of fuzzy set theory, I only want to claim that we can utilize the idea of degrees of set membership but not that we have to endorse the whole fuzzy set-theoretical package.
If we were to allow evaluation of counterfactuals across arbitrary worlds in stratified modal space, we would have to allow for more a complex—perhaps even degree-theoretical—semantics for counterfactuals. As long as we assume that the actual world is a world in which classical logic holds, however, we can forget about these other truth-values in explicating (ConFac).
Cf. Nolan (1997, p. 550).
(Entailment Principle) is a version of a similar principle in the standard Lewis–Stalnaker semantics that allows us to infer A
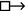 C whenever C is a (classical) logical consequence of A.
C whenever C is a (classical) logical consequence of A.Alternatively, we can make (2) false, according to (S-ConFac), by stipulating that the explosion world is not in \({W_{{\mathcal{L}_{IL}}}}\).
Notice that the antecedent in (18) does not assume that the logic L is correct (true, adequate). As such, (Relative Closeness Condition) does not apply in this context.
Nolan raises an objection along those lines (Nolan 1997, pp. 547–548).
Notice also that the specification of \({W_{\mathcal{L}_X}}\) allows us to validate extensionally the following principle that Nolan (1997) tentatively subscribes to:
(Comprehension Principle) For any set \(\Updelta\) of sentences that cannot possibly be jointly true, there is an impossible world in which each sentence in \(\Updelta\) is true.
For given that there are no—or hardly any—principles governing logical consequence in \(\mathcal{L}_X\), any set of sentences—or almost any set of sentences—will count as a world in \({W_{\mathcal{L}_X}}\).
References
Adams, R. (1974). Theories of actuality. Nous, 8, 211–231.
Berto, F. (2009). Impossible worlds. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy (Winter 2003 Edition). http://plato.stanford.edu/entries/impossible-worlds/. Accessed 12 April 2013.
Brogaard, B., & Salerno, J. (2013). Remarks on counterpossibles. Synthese, 190, 639–660.
Carnap, R. (1947). Meaning and necessity, a study in semantics and modal logic. Chicago: University of Chicago Press.
Chalmers, D. J. (2011). The nature of epistemic space. In A. Egan & B. Weatherson (Eds.), Epistemic modality (pp. 60–107). New York: Oxford University Press.
Goodman, J. (2004). An extended Lewis/Stalnaker semantics and the new problem of counterpossibles. Philosophical Papers, 33, 35–66.
Hintikka, J. (1969). Models for modalities. Dordrecht: D. Reidel Publishing Company.
Jeffrey, R. (1983). The logic of decision. Chicago: University of Chicago Press.
Krakauer, B. (2012). What are impossible worlds? In Philosophical Studies (online first), 1–19. doi:10.1007/s11098-012-9998-0.
Lewis, D. (1973). Counterfactuals and comparative possibility. Journal of Philosophical Logic, 2, 418–446.
Lewis, D. (1986). On the plurality of worlds. Oxford: Blackwell Publishers.
Mares, E. (1997). Who’s afraid of impossible worlds? Notre Dame Journal of Formal Logic, 38, 516–526.
Nolan, D. (1997). Impossible worlds: A modest approach. Notre Dame Journal for Formal Logic, 38, 325–527.
Stalnaker, R. (1968). A theory of conditionals. In Studies in logical theory, American Philosophical Quarterly Monograph Series, 2 (pp. 98–112). Oxford: Blackwell.
Vander Laan, D. (2004). Counterpossibles and similarity. In F. Jackson & G. Priest (Eds.), Lewisian themes (pp. 258–276). Oxford: Oxford University Press.
Williamson, T. (2007). The philosophy of philosophy. Oxford: Blackwell.
Acknowledgments
I am grateful to Daniel Nolan, Weng Hong Tang, and an anonymous referee for Philosophical Studies for extremely helpful comments on an earlier draft of this paper. Thanks also to Jørgen Berthelsen, Eline Busck Gundersen, Asbjørn Steglich-Petersen, and audience in the Research Unit for Epistemology, Metaphysics, and Philosophy of Cognition at Aarhus University.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
In this appendix, I give the proofs of (Satisfiability) and (Inc).
Proof of (Satisfiability)
Let \(\Upgamma\) be any set of sentences that satisfies (i) and (ii) in (Satisfiability). We want to show that there is a propositional evaluation function ν that makes each sentence A in \(\Upgamma\) true. To this end, we stipulate an interpretation \(\mathcal{I}\) such that for all atomic A:
\(\mathcal{I}(A) = T\) iff \(A \in \Upgamma\).
\(\mathcal{I}(A) = F\) iff \(A \notin \Upgamma\).
This is a possible stipulation because \(\mathcal{I}\) cannot assign both T and F to any atomic A. We then need to show that every sentence in \(\Upgamma\) is true under this interpretation. I do this by induction on the length of a sentence, where the length of a sentence is given by the number of symbols it contains:
-
Base case: Assume for atomic A that \(A \in \Upgamma\). We want to show that ν(A) = T. We get the result immediately. By definition of \(\mathcal{I}, A \in \Upgamma\) iff \(\mathcal{I}(A) = T\). By (\(\nu\mathcal{I}\)), \(\mathcal{I}(A) = T\) iff ν (A) = T. So \(A \in \Upgamma\) iff ν(A) = T. So ν(A) = T.
-
Inductive step: Assume for the induction hypothesis that every sentence in \(\Upgamma\) that is shorter than \(\neg A\) and (A ∧ B) is true under the evaluation ν based on \(\mathcal{I}\). We want to show that if \(\neg A \in \Upgamma\), then \(\nu(\neg A) = T\), and if \((A \wedge B) \in \Upgamma\), then ν (A ∧ B) = T. There are two cases to consider:
-
Case 1: Assume \(\neg A \in \Upgamma\). By (i) in (Satisfiability), \(\neg A \in \Upgamma\) iff \(A \notin \Upgamma\). By induction hypothesis, \(A \notin \Upgamma\) iff ν(A) = F. By (\(\nu\neg\)) in (Evaluation), ν(A) = F iff \(\nu(\neg A) = T\). So \(\nu(\neg A) = T\).
-
Case 2: Assume \((A \wedge B) \in \Upgamma\). By (ii) in (Satisfiability), \((A \wedge B) \in \Upgamma\) iff \(A \in \Upgamma\) and \(B \in \Upgamma\). By induction hypothesis, \(A \in \Upgamma\) and \(B \in \Upgamma\) iff ν(A) = T and ν(B) = T. By (ν∧) in (Evaluation), ν(A) = T and ν(B) = T iff ν(A ∧ B) = T. So ν(A ∧ B) = T. □
Proof of (Inc)
Let \(\Updelta\) be any maximal, logically inconsistent set of sentences. By (Satisfiability), \(\Updelta\) will fail to satisfy either (i) or (ii) and hence contain at least one of the following inconsistent pairs or triples of sentences:
-
Case 1: \(\Updelta\) may be inconsistent because it fails to satisfy (i) of (Satisfiability), in which case \(\Updelta\) contains an inconsistency of the form \(\{A, \neg A\}\). That is, \(\Updelta\) contains an instance of a LNC-inconsistency.
-
Case 2: \(\Updelta\) may be inconsistent because it fails to satisfy (ii) of (Satisfiability), in which case \(\Updelta\) contains either an inconsistency of the form \(\{\neg A, (A \wedge B)\}, \{\neg B, (A \wedge B)\}\), or \(\{\neg A, \neg B, (A \wedge B)\}\), or an inconsistency of the form \(\{A, B, \neg(A \wedge B)\}\). That is, \(\Updelta\) contains either an instance of a CF-inconsistency or an instance of a NCF-inconsistency. □
Rights and permissions
About this article
Cite this article
Bjerring, J.C. On counterpossibles. Philos Stud 168, 327–353 (2014). https://doi.org/10.1007/s11098-013-0133-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11098-013-0133-7




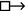 C whenever C is a (classical) logical consequence of A.
C whenever C is a (classical) logical consequence of A.