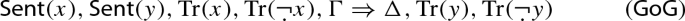Abstract
This article compares classical (or KF-like) and nonclassical (or PKF-like) axiomatisations of the fixed-point semantics developed by Kripke (J Philos 72(19): 690–716, 1975). Following the line of investigation of Halbach and Nicolai (J Philos Logic 47(2): 227–257, 2018), we do not compare KF and PKF qua theories of truth simpliciter, but rather qua axiomatisations of the Kripkean conception of truth. We strengthen the central results of Halbach and Nicolai (2018) and Nicolai (Stud Log 106(1): 101–130, 2018), showing that, on the one hand, there is a stronger sense in which some variants of KF and some variants of PKF can be taken to be, truth-theoretically, equivalent. On the other hand, we show that this truth-theoretical equivalence is not preserved by some other variants of KF and PKF, arguing that the PKF variants are more adequate axiomatisations of the fixed-point semantics than the corresponding KF variants.
Similar content being viewed by others
1 Introduction
The use of nonclassical logics is extensive in the development of formal theories of truth. Probably the most popular semantic theory of truth formulated in nonclassical logic is Kripke’s fixed-point semantics Kripke (1975). This semantic conception of truth lends itself to being axiomatised in classical logic as well as in noncalssical logic. Classical axiomatisations are variants of the theory known as Kripke-Feferman (KF); nonclassical axiomatisations are variants of the nonclassical theory known as Partial-Kripke-Feferman (PKF).Footnote 1
KF and PKF (and variants thereof) have been often compared in the literature, and they have both been defended and criticised on different grounds. Defenders of KF (e.g. Halbach 2014; Halbach and Nicolai 2018) point out that KF is mathematically much stronger than PKF—KF proves more arithmetical statements than PKF—and proof-theoretic strength is often taken to be a virtue of a theory of truth. Thanks to recent work by Halbach and Nicolai, we have now a better grasp on the source of this asymmetry in the proof-theoretic strengths of KF and PKF: Halbach and Nicolai (2018) have crucially shown that, once the schema of induction is restricted to the arithmetical vocabulary, KF and PKF have the same truth-free consequences and they prove the same sentences to be true. This indicates clearly that the deductive weakness of PKF does not arise from a lack of truth-theoretic resources that are on the contrary available to KF. It is the use of nonclassical logic that, paralysing inductive reasoning on sentences containing the truth predicate \(\mathrm {Tr}\), has profound consequences on the arithmetical statements derivable in the system.Footnote 2
Defenders of PKF (e.g. Field 2008; Horsten 2009), on the other hand, argue that PKF is more adequate from a conceptual point of view, notwithstanding its mathematical weakness.Footnote 3 Hartry Field, for example, argues that PKF-like theories are far superior than KF-like theories. One of the main advantages of PKF is that it exploits what (Field 2008, p. 69) calls the “raison d’être of fixed points”, i.e., the complete equivalence between \(\varphi \) and \(\mathrm {Tr} (\varphi )\), for any sentence, in any context. It is known, in fact, that the truth predicate of PKF is fully transparent, which means that it is always possible to infer \(\mathrm {Tr} (\varphi )\) from \(\varphi \), and vice versa. By contrast, a problem often associated with KF is its asymmetry, that is the fact that there are sentences \(\varphi \) such that \(\varphi \) is derivable, but \(\mathrm {Tr} (\varphi )\) is not.Footnote 4
In this paper, we will also compare KF and PKF. However, the line of investigation will be different. We will not rely on the strength on KF to dismiss the use of nonclassical logic, nor shall we rely on the asymmetry of KF to argue that PKF is conceptually more adequate. We will not rely on the transparency of \(\mathrm {Tr}\) in PKF to discard the use of classical logic, nor shall we emphasise that in PKF “nothing like sustained ordinary reasoning can be carried on” (Feferman 1984, p. 95). The reason is that we are not going to compare KF and PKF qua theories of truth simpliciter. And we are not going to ask whether one theory is more adequate than the other, in absolute terms. What we would like to do, instead, is to compare KF and PKF qua axiomatisations of the fixed-point semantics. We would like to ask whether one theory is more adequate than the other as axiomatisation of the Kripkean conception of truth.
The interest in this analysis has been triggered by the already mentioned paper by Halbach and Nicolai—titled “On the costs of nonclassical logic”—where they also compare KF and PKF qua axiomatisations of the fixed-point semantics. Halbach and Nicolai (2018) warn that the costs of abandoning classical logic might go beyond the initial expectations of the defender of PKF. The crucial claims defended by Halbach and Nicolai are that
the use of nonclassical logic of PKF does not affect the truth-theoretic content [and] the [Kripkean] conception of truth [...] is captured equally well by the nonclassical theory PKF and by the classical theory KF. (Halbach and Nicolai 2018, p. 228; p. 241)
Clearly, the proof-theoretic weakness of PKF, in itself, is not enough to justify the rejection of nonclassical logic in axiomatisations of the fixed-point semantics. It could for example be the case that the Kripkean conception of truth can be adequately axiomatised only within a nonclassical system, in which case we would need to use nonclassical logic, despite its costs. But if – as claimed by Halbach and Nicolai (2018)—KF captures the Kripkean conception of truth as adequately as PKF, then this would nourish philosophical doubts vis-à-vis the use of nonclassical logic: Why would we cripple our ordinary reasoning if we can axiomatise the target conception of truth using classical logic? If, however, one can show that PKF is more adequate than KF (let us reiterate: not as a truth theory simpliciter, but as axiomatisation of the fixed-point semantics), then one would have to reconsider whether employing nonclassical logics is or is not worth. That is why we would like to ask whether KF and PKF can be taken to capture the Kripkean conception of truth equally well and/or whether they can be said to have the same truth-theoretic content.
The answer emerging from some results presented in this article will be “it depends”. On the one hand, by strengthening the central results by Halbach and Nicolai (2018) and Nicolai (2018), it will be shown that there are compelling reasons for believing that some variants of KF and PKF are, truth-theoretically, on a par. On the other hand, it will also be shown that there are other variants of KF and PKF that cannot be said to capture the Kripkean conception of truth equally well, nor can they be taken to have the same truth-theoretic content. By inspecting these theories, it turns out that there is one specific aspect of the Kripkean conception of truth that can be captured only by the PKF-variants, but not by the corresponding KF-variants. The aspect we are referring to is that in fixed-point models, ‘being untrue’ and ‘being false’ (i.e., having a true negation) are coextensive properties. As it will become clear below, this is not an accidental property of the Kripkean conception of truth, but rather one of its constitutive features. It can be shown that while every variant of PKF does embody the coextensiveness of untruth and falsity, the same cannot be said for KF: within some of its variants, being untrue and being false are different properties. This discrepancy between proof theory and semantics, it will be argued, indicates that not only nonclassical logic, but also classical logic has its own costs, and that the lack of a transparent truth-predicate may well not be its highest.
1.1 Structure and Key Points of the Paper
What follows can be divided into two parts and a technical appendix. The first part comprises Sect. 2 and Sect. 3. In Sect. 2 we explain what is meant by ‘Kripkean conception of truth’, why Halbach and Nicolai (2018) maintain that this conception is embodied equally well by KF and PKF, and why they claim that KF and PKF have the same truth-theoretic content. This amounts to introducing two criteria: the first establishes when an axiomatic system can be said to capture a semantic construction; the second is a method for comparing the truth-theoretic content of two axiomatic systems. In §3, relying on two counterexamples (Example 6 and Example 8), we first point out that the criteria employed by Halbach and Nicolai (2018) are too coarse-grained, and we then suggest a way to refine them. We conclude the first part of the article by implementing the new, finer-grained criteria: We show that the central theorems of Halbach and Nicolai (2018) and Nicolai (2018) can be made stronger, thereby providing additional support to the claim that some variants of KF and PKF can be seen as being, truth-theoretically, equivalent. The second part, §4 and §5, is the reason behind the title of this article: It will be shown that two variants of KF cannot be said to capture the Kripkean conception of truth as adequately as their PKF-counterparts, which amounts to the price we have to pay for axiomatising the Kripkean semantics using classical logic.
1.2 Preliminaries and Notation
Formalism is kept to a minimum in the main body of the paper, and all technical details are contained in an appendix. However, the philosophical points suggested here rely on some original formal results, without which our claims about KF and PKF would lose both support and interest. Hence, some formalism will be used below, for which we now fix a modicum of notation and preliminaries, assuming the reader being familiar with Kripke (1975). As background theory of syntax we use Peano arithmetic, PA. \(\mathcal {L}_{\textsf {PA} }\) is the language of arithmetic, and \(\mathcal {L} _\mathrm {Tr} \) is \(\mathcal {L}_{\textsf {PA} } \cup \{\mathrm {Tr} \}\). We abuse notation and write \(\mathrm {Tr} (\varphi )\) instead of \(\mathrm {Tr} \ulcorner {\varphi }\urcorner \), where \(\ulcorner {\varphi }\urcorner \) is the numeral of the Gödel number of \(\varphi \). Given a theory \(\mathrm {Th}\), we let ‘\(\mathrm {Th} \vdash \varphi \)’ symbolise a definition of the \(\mathrm {Th}\)-derivability of \(\varphi \).
A four-valued model for \(\mathcal {L} _\mathrm {Tr} \) is a structure \(\langle \mathcal {N}, (E, A)\rangle \) such that \(\mathcal {N}\) is a model for \(\mathcal {L}_{\textsf {PA} }\) and (E, A) is a pair of subsets of \(|{\mathcal {N}}|\) (the support of \(\mathcal {N}\)) interpreting \(\mathrm {Tr}\). We also refer to structures \(\langle \mathcal {N}, (E, A)\rangle \) as FDE-structures. The standard model of PA is denoted by \(\mathbb {N}\). The relation  expresses that \(\varphi \) is FDE-satisfied in the structure \(\langle \mathbb {N}, (E, A)\rangle \). Moreover, we say that an FDE-structure \(\langle \mathbb {N}, (E, A)\rangle \) is
expresses that \(\varphi \) is FDE-satisfied in the structure \(\langle \mathbb {N}, (E, A)\rangle \). Moreover, we say that an FDE-structure \(\langle \mathbb {N}, (E, A)\rangle \) is
-
a \(\textsf {K} \mathsf {3}\)-structure, if \(E \cap A = \varnothing \),
-
a LP-structure, if \(E \cup A = \omega \),
-
a \(\textsf {KS} \mathsf {3}\)-structure, if it is either \(\textsf {K} \mathsf {3}\) or LP,
-
a CL-structure, if \(A = \omega - E\).
\(\textsf {Sent} \) is the set of (codes of) sentences, and \(\textsf {NSent} :=\omega -\textsf {Sent} \). The Kripke Jump is a function \(\Phi :\wp (\omega )^2\longrightarrow \wp (\omega )^2\) on pairs of subsets of natural numbers defined as

A fixed-point of \(\Phi \) is a pair (E, A) such that \(\Phi (E, A)=(E, A)\). A fixed-point model for \(\mathcal {L} _\mathrm {Tr} \) is an FDE-structure \(\langle \mathbb {N}, (E, A)\rangle \) where \((E, A)=\Phi (E, A)\). A fixed-point model is
-
consistent, if it is a \(\textsf {K} \mathsf {3}\)-structure,
-
complete, if it is a LP-structure,
-
symmetric, if it is a \(\textsf {KS} \mathsf {3}\)-structure.
By KF and PKF we mean the truth-systems that admit both truth-value gluts (sentences which are both true and false) and truth-value gaps (sentences which are neither true nor false). We work with KF and PKF formulated over two-sided sequent calculi. \(\textsf {KF} _\textsf {S} \) and \(\textsf {PKF} _\textsf {S} \) are so called symmetric variants, i.e., they are theories excluding the simultaneous occurrence of gaps and gluts. \(\textsf {KF} _\textsf {S} \) can be obtained from KF by adding the axiom

and \(\textsf {PKF} _\textsf {S} \) can be obtained from PKF by adding the axiom

Both GoG and GG stand for “gaps or gluts”.
We also study variations on the induction schema.Footnote 5 In particular, given \(\mathrm {Th}\in \{\textsf {KF} , \textsf {KF} _\textsf {S} , \textsf {PKF} , \textsf {PKF} _\textsf {S} \}\), we let
-
\(\mathrm {Th}^- \) be the theory obtained from \(\mathrm {Th}\) by restricting the induction schema to arithmetical-formulae;
-
\(\mathrm {Th}^\mathsf{int }\) be the theory obtained from \(\mathrm {Th}^- \) by replacing the restricted version of induction with the schema of internal induction;
-
\(\mathrm {Th}^+\) be the theory obtained by extending \(\mathrm {Th}\) with the schema of transfinite induction up to any ordinal below \(\varepsilon _0\).Footnote 6
2 Halbach & Nicolai’s Criteria
As mentioned in the introduction, we want to verify whether KF and PKF can be said to capture the Kripkean conception of truth equally well. Following Halbach and Nicolai (2018), by ‘Kripkean conception of truth’ we mean the nonclassical understanding of it, that is, we understand KF as a classical system that describes a compositional, self-applicable, transparent, nonclassical notion of truth (compare (Halbach and Nicolai 2018, Sect. 2)). Technically, this means that we will be looking at classes of fixed-point models in their nonclassical version, with truth-value gaps and/or gluts.Footnote 7\(^,\)Footnote 8
2.1 \(\varvec{\mathbb {N}}\)-categoricity
The claim that an axiomatic system captures a certain semantic construction is in need of clarification, especially if the logic of the formal system does not coincide with the logic of the semantic construction. A criterion commonly employed in literature (and in particular by Halbach and Nicolai (2018)), establishing when an axiomatic theory of truth can be said to capture a semantic theory, is the criterion known as ‘\(\mathbb {N}\)-categoricity’. The idea behind this criterion, introduced by Fischer et al. (2015), is that an axiomatic system S captures a semantic theory \(\mathfrak {S}\) if the standard models of S are exactly the standard models in \(\mathfrak {S}\), where a ‘standard model’ is a model expanding the standard model \(\mathbb {N}\) with an interpretation for \(\mathrm {Tr}\).
In order to make this idea rigorous and provide a formal definition, we restrict our attention to a specific kind of semantic theories of truth. Since we will be dealing only with classical and fixed-point models, we define a semantic theory of truth to be a class \(\mathfrak {S}\) of models \(\langle \mathcal {N}, (E, A)\rangle \) for \(\mathcal {L} _\mathrm {Tr} \), where \(\mathcal {N}\) interprets \(\mathcal {L}_{\textsf {PA} }\), and the pair (E, A) is an interpretation for \(\mathrm {Tr}\), where E (A) is called the (anti-)extension of \(\mathrm {Tr}\). An important observation about classical and fixed-point models is that A is definable via E. More precisely:
Remark 1
-
In classical models, the anti-extension A is definable as the complement of the extension E.
-
Given a fixed-point \((E, A)=\Phi (E, A)\) of the Kripke Jump \(\Phi \), the anti-extension A is definable via E as
$$\begin{aligned} A:=\{\varphi \in \textsf {Sent} \mid \lnot \varphi \in E\}\cup \textsf {NSent}. \end{aligned}$$
For notational convenience, then, we often drop A and we let a semantic truth theory be a class \(\mathfrak {S}\) of structures \((\mathcal {N}, E)\) where \(\mathcal {N}\) is an interpretation of \(\mathcal {L}_{\textsf {PA} }\) and E an interpretation of \(\mathrm {Tr}\), implicitly assuming that A can be defined via E. Also, we often write that \(E=\Phi (E)\) is a fixed-point of \(\Phi \).
Having clarified the type of semantic theory we will be dealing with, we can now introduce the \(\mathbb {N}\)-categoricity criterion.Footnote 9
Criterion 2
(\(\mathbb {N}\)-categoricity) Let \(\mathrm {Th}\) be an axiomatic \(\mathcal {L} _\mathrm {Tr} \)-theory formulated in the logic L; let  be the class of standard models of \(\mathrm {Th}\); let \(\mathfrak {S}\) be a semantic theory, and let \(\mathfrak {S} ^\mathbb {N}:=\{(\mathbb {N}, E)\mid (\mathbb {N}, E)\in \mathfrak {S} \}\) be the class of standard models in \(\mathfrak {S} \). \(\mathrm {Th}\) is an adequate axiomatisation of \(\mathfrak {S} \) if and only if,
be the class of standard models of \(\mathrm {Th}\); let \(\mathfrak {S}\) be a semantic theory, and let \(\mathfrak {S} ^\mathbb {N}:=\{(\mathbb {N}, E)\mid (\mathbb {N}, E)\in \mathfrak {S} \}\) be the class of standard models in \(\mathfrak {S} \). \(\mathrm {Th}\) is an adequate axiomatisation of \(\mathfrak {S} \) if and only if,
Criterion 2 imposes that the class of the extensions of \(\mathrm {Tr}\) in standard models of \(\mathrm {Th}\) be ‘sound’ and ‘complete’ relative to the class of the extensions of \(\mathrm {Tr}\) in standard models in \(\mathfrak {S}\). Sound in the sense that, whenever E is the extension of \(\mathrm {Tr}\) in a \(\mathbb {N}\)-model of \(\mathrm {Th}\), then E is the extension of \(\mathrm {Tr}\) in a \(\mathbb {N}\)-model in \(\mathfrak {S}\); complete in the sense that, whenever E is the extension of \(\mathrm {Tr}\) in a \(\mathbb {N}\)-model in \(\mathfrak {S}\), then E is the extension of \(\mathrm {Tr}\) in a \(\mathbb {N}\)-model of \(\mathrm {Th}\). More intuitively, this criterion requires that \(\varphi \) is true in a \(\mathbb {N}\)-model of \(\mathrm {Th}\) precisely when \(\varphi \) is true in a \(\mathbb {N}\)-model in \(\mathfrak {S}\).
It is worth observing that the Criterion 2 does not imply that \(\mathfrak {M} ^\mathbb {N} =\mathfrak {S} ^\mathbb {N} \). In fact, the logic L in which the theory \(\mathrm {Th}\) is formulated need not coincide with the logic of the semantic theory \(\mathfrak {S}\). As a consequence, the way in which A is definable in the structures of \(\mathfrak {M} ^\mathbb {N} \) need not be equivalent to the way in which A is definable in the structures of \(\mathfrak {S}^\mathbb {N} \). For example, if we let \(\mathfrak {S}^\mathbb {N} \) be the class of fixed-point models for \(\mathcal {L} _\mathrm {Tr} \), and if we let L be classical logic, then \(\mathfrak {S}^\mathbb {N} \) would contain FDE-structures \(\langle \mathbb {N}, (E, A)\rangle \) such that \(E=\Phi (E)\) and \(A:=\{\varphi \in \textsf {Sent} \mid \lnot \varphi \in E\}\cup \textsf {NSent} \), whereas \(\mathfrak {M} ^\mathbb {N} \) would contain classical structures \(\langle \mathbb {N}, (E, A)\rangle \) where \(E=\Phi (E)\) and \(A=\omega -E\).
It is well known that both KF and PKF are—in the sense just described—adequate axiomatisations of the fixed-point semantics. That is,
Theorem 3
(Feferman 1991; Halbach and Horsten 2006) Let \(\mathcal {K}:=\{(\mathbb {N}, E)\mid E=\Phi (E)\}\) be the class of fixed-point models for \(\mathcal {L} _\mathrm {Tr} \); let \(\mathcal {M} ^\textsf {KF} :=\{(\mathbb {N}, E)\mid (\mathbb {N}, E)\models \textsf {KF} \}\) be the class of standard models of KF; let  be the class of standard models of PKF. Then
be the class of standard models of PKF. Then

Relative to the \(\mathbb {N}\)-categoricity criterion, then, KF and PKF can be said to capture the Kripkean conception of truth equally well.Footnote 10 The qualification before the comma is necessary. As emphasized by Halbach and Nicolai (2018), in fact, the \(\mathbb {N}\)-categoricity criterion can at best be seen as a necessary condition an axiomatic theory has to satisfy in order to capture a semantic construction. A number of issues are connected with Criterion 2,Footnote 11 and it is not difficult to see that even if two axiomatic theories \(\mathrm {Th}\) and \(\mathrm {Th'}\) are \(\mathbb {N}\)-categorical axiomatisations of a semantic theory \(\mathcal {M}\), this does not imply that \(\mathcal {M}\) is captured equally well by \(\mathrm {Th}\) and \(\mathrm {Th'}\), nor can we infer that \(\mathrm {Th}\) and \(\mathrm {Th'}\) embody the same conception of truth. An example showing this point vividly will be provided below (see Example 8). Before that, however, let us explain how Halbach and Nicolai compare KF and PKF qua formal systems, and why they claim that these theories have the same truth-theoretic content.
2.2 Inner Theory
After having established that there is a precise sense in which KF and PKF can be taken to embody the same conception of truth, Halbach and Nicolai (2018) move on to compare the two theories qua formal systems. A comparison of the conceptual aspects of axiomatic theories of truth—what could be called their ‘truth-theoretic content’—is a non-trivial task, and sophisticated methods of analysis have been developed. Unfortunately, several of these tools, like relative interpretability or the finer-grained relative truth definability introduced by Fujimoto (2010), cannot be used for comparing KF and PKF: These methods are not suitable for comparing theories formulated in different logics.
In the spirit of Reinhardt (1985, 1986), and following up on the line of investigation initiated by Halbach and Horsten (2006), Halbach and Nicolai compare KF and PKF via what is usually called their ‘inner theory’, i.e., they compare the sets of sentences that are provably true in each theory.Footnote 12 Recall that ‘\(\mathrm {Th} \vdash \varphi \)’ symbolises a definition of the \(\mathrm {Th}\)-derivability of \(\varphi \). Then
Definition 4
(Inner Theory) Let \(\mathrm {Th}\) be a truth theory formulated in \(\mathcal {L} _\mathrm {Tr} \). The inner theory of \(\mathrm {Th}\), \(\mathrm {I} \mathrm {Th} \), is defined thus:
Concentrating on the set of provably true sentences allows a neat comparison between KF-like and PKF-like theories. The reason is that
which means that PKF-like theories are identical to their internal theories. An important consequence of this observation is that, whereas it is not useful to ask whether KF is contained in PKF,Footnote 13 a key question is whether the inner theory of KF is contained in PKF and/or vice versa.Footnote 14
Halbach and Nicolai (2018) and Nicolai (2018), building on previous results by Halbach and Horsten (2006), have analysed the relationship between the inner theories of several variants of KF and corresponding variants of PKF. They have shown a thorough equivalence between them: Given a KF-like theory, there is a corresponding PKF-like theory such that the set of provably true sentences of the former coincide with the set of theorems of the latter. In other words, they proved the following remarkableFootnote 15
Theorem 5
(Halbach and Horsten 2006; Halbach and Nicolai 2018; Nicolai 2018) Let \((\textsf {PKF} _\star , \textsf {KF} _\star )\) range over the following theory-pairs

Then
Let us emphasise that the claim that KF and PKF embody the same conception of truth is a consequence of their being \(\mathbb {N}\)-categorical axiomatisations of the fixed-point semantics, not a consequence of their having the same inner theory.Footnote 16 The analysis of the inner theories of KF and PKF is a second step: After having established that a classical and a nonclassical system are both \(\mathbb {N}\)-categorical axiomatisations of a certain semantics, one can compare these theories qua formal systems, asking whether they prove the same sentences to be true, or whether one theory is truth-theoretically stronger than the other.
3 Finer-Grained Criteria
This section begins by refining the criteria just introduced. Examples 6 and 8 below show that they are too coarse-grained. As it will become evident, both examples indicate that the set of provably not-true sentences plays a crucial role:Footnote 17 Some of the aspects relating a formal system and a semantic theory on the one hand, and some of the aspects relating and/or differentiating two formal systems on the other, materialise only if we take into account what the theories prove to be not-true. In what follows, then, we include the concept of the anti-extension of \(\mathrm {Tr}\) in a refinement of the above criteria and we discuss the implications of this inclusion. As mentioned in the introduction, this finer-grained analysis (i) will strengthen the central results presented in the previous section, i.e., Theorems 3 and 5, and (ii) will show that there is a key aspect of the Kripkean semantics that some variants of KF cannot capture as adequately as their PKF-counterparts.
Before we begin, a caveat is in order. A tacit assumption underlying the present study is that it is possible (in principle, at least) for a classical system to embody a transparent, nonclassical conception of truth. The results presented in this section contain insofar a defence of classical logic, as it will be shown that a truth-theoretical equivalence between classical and nonclassical systems can be established under criteria which are stricter than those commonly employed. Of course, the nonclassical logician can always reject this assumption and argue that the very same idea of axiomatising the Kripkean conception of truth using classical logic is a non-starter, as KF is asymmetric. In fact, more is true: (Halbach and Horsten 2006, p. 688) have observed that “KF is essentially asymmetric”, in the sense that KF cannot be consistently closed under the rules of Necessitation and Co-Necessitation

In other words, we cannot even consistently postulate that outer theory (what is provable) and inner theory (what is provably true) of KF are identical. But being symmetric, it may be argued, is a sine qua non for being considered an adequate axiomatisation of the fixed-point semantics, hence no KF variant could be said to embody the Kripkean conception of truth.Footnote 18 As already mentioned in the Introduction, however, in this article we would like to shift the focus of contention, examining the relationship between KF and PKF from a different perspective: We will neither rely on the asymmetry of KF to argue against classical logic, nor on the weakness of PKF to argue against nonclassical logic.
3.1 Refining Inner Theory
One may wonder whether analysing the relationship between the inner theory of a classical system with the inner theory of a nonclassical alternative is sufficient to understand how they are related to each other from a conceptual point of view. For, if one is interested in comparing the truth-theoretic aspects of two theories, concentrating only on what is provably true in each system might not be enough. There could in fact be other aspects relating and/or differentiating the theories which may emerge only if we implement a finer-grained method of comparison.
The set of provably true sentences, no doubt, is an important component in the analysis of the truth-theoretic content of a truth theory. Observe, however, that for any theory \(\mathrm {Th}\) we can consider the following sets:Footnote 19

Let \(\mathrm {Th} ^E, \mathrm {Th} ^A\), and \(\mathrm {Th} ^F\) be the extension, anti-extension, and falsity-set, respectively, induced by \(\mathrm {Th}\). Analysing the relationship between these sets, we can read off from \(\mathrm {Th}\) considerably more than \(\mathrm {I} \mathrm {Th} \) (here \(\mathrm {Th} ^E\)). For instance, one could ask whether \(\mathrm {Th}\) thinks that being untrue and being false are coextensive properties, i.e., one could ask whether \(\mathrm {Th} ^A = \mathrm {Th} ^F\)? Or one could ask whether \(\mathrm {Th}\) thinks that every sentence is either true or untrue, i.e., whether \({\textsf {Sent}} \subseteq \mathrm {Th} ^E \cup \mathrm {Th} ^A\)? Or whether there are sentences that are both true and untrue, i.e., whether \(\mathrm {Th} ^E \cap \mathrm {Th} ^A \ne \varnothing ?\) And so forth.
Arguably, statements about being not-true and statements about being false are ipso facto statements about truth. It thus seems that the inner theory of \(\mathrm {Th}\) is only one component of its overall view on truth. \(\mathrm {Th} ^A\), and its relationship with \(\mathrm {Th} ^E\), is not less relevant. To see this point vividly, consider the following
Example 6
Let \(\mathrm {Th}\) and \(\mathrm {Th'}\) be two \(\mathcal {L} _\mathrm {Tr} \)-theories, and suppose that \(\mathrm {Th} ^E = \mathrm {Th'} ^E\), i.e., suppose
Suppose further that \(\mathrm {Th} ^A \ne \mathrm {Th'} ^A\). Then we could for instance have \(\mathrm {Th} ^A = \mathrm {Th} ^F\), i.e.

but possibly \(\mathrm {Th'} ^A \not \subset \mathrm {Th'} ^F\), i.e.

This means that ‘being not-true’ and ‘being false’ are coextensive properties according to \(\mathrm {Th}\), but not according to \(\mathrm {Th'}\). Therefore, if we were to compare \(\mathrm {Th}\) and \(\mathrm {Th'}\) only with respect to the sentences they prove to be true, we’d wrongly be lead to the conclusion that \(\mathrm {Th}\) and \(\mathrm {Th'}\) had the same truth-theoretic content, even though there is a straightforward sense in which \(\mathrm {Th}\) ’s and \(\mathrm {Th'}\) ’s views on truth are different and, to some extent, incompatible. \(\square \)
Our idea behind the refinement of the criterion for comparing KF and PKF qua formal systems is now rather simple: We will ask not only how the sets
are related to each other. We will in addition ask how the sets
are related to each other.
Since the use of ‘inner theory’ is already quite extensive in the literature, we use ‘truth-theoretic content’ instead, as this notion has been used by Halbach and Nicolai (2018) interchangeably with inner theory.Footnote 20
Definition 7
(Truth-theoretic content) Let \(\mathrm {Th}\) be a \(\mathcal {L} _\mathrm {Tr} \)-theory. The truth-theoretic content of \(\mathrm {Th}\), \(\mathrm {Th} ^\text {ttc} \), is defined as follows.

Using the notation introduced above, we have
According to Definition 7, a sentence \(\varphi \) is part of the truth-theoretic content of \(\mathrm {Th}\) whenever \(\mathrm {Th}\) has something to say about the truth status of \(\varphi \), i.e., whenever \(\varphi \) is provably true, or provably untrue.
3.2 Refining \(\mathbb {N}\)-categoricity
A counterexample very similar to Example 6 can be constructed to show that \(\mathbb {N}\)-categoricity criterion, too, needs to be refined.
Example 8
Let \(\mathfrak {S}\) be a semantic theory such that the anti-extension A can be defined via E, say in a Kripkean fashion as
so that ‘being not-true’ and ‘being false’ are coextensive properties.
Now let \(\mathrm {Th}\) and \(\mathrm {Th'}\) be two theories formulated in the logics L and \(L'\), respectively. Suppose further that both \(\mathrm {Th}\) and \(\mathrm {Th'}\) are \(\mathbb {N}\)-categorical axiomatisations of \(\mathcal {M}\), i.e., suppose

This is compatible with two further assumptions, i.e.

\(\mathrm {Th}\) and \(\mathrm {Th'}\) can hardly be taken to embody the same conception of truth, let alone to capture \(\mathfrak {S}\) equally well: In \(\mathrm {Th}\) ‘being not-true’ and ‘being false’ are coextensive properties, in \(\mathrm {Th'}\) they are not. Indeed, one could argue that \(\mathrm {Th'}\) does not embody the conception of truth conveyed by \(\mathfrak {S}\), as they don’t agree on whether untruth and falsity are coextensive. It seems thus uncontroversial that Criterion 2 is too coarse-grained to establish whether two theories can be said to capture a certain semantics equally well. \(\square \)
Our idea behind the refinement of the \(\mathbb {N}\)-categoricity criterion is now as simple as the idea behind the refinement of the notion of inner theory. We will not only require that the class of the extensions of \(\mathrm {Tr}\) in \(\mathbb {N}\)-models of \(\mathrm {Th}\) be ‘sound’ and ‘complete’ relative to the class of the extensions of \(\mathrm {Tr}\) in \(\mathbb {N}\)-models in \(\mathfrak {S}\). We will additionally require that the class of the anti-extension of \(\mathrm {Tr}\) in \(\mathbb {N}\)-models of \(\mathrm {Th}\) be ‘sound’ and ‘complete’ relative to the class of the anti-extensions of \(\mathrm {Tr}\) in \(\mathbb {N}\)-models in \(\mathfrak {S}\). To put it intuitively: Whereas Criterion 2 only requires that \(\varphi \) is true in a standard model of \(\mathrm {Th}\) iff \(\varphi \) is true in a standard model in \(\mathfrak {S}\), the finer-grained criterion introduced below additionally requires that \(\varphi \) is not-true in a standard model of \(\mathrm {Th}\) iff \(\varphi \) is not-true in a standard model in \(\mathfrak {S}\).
To give this idea formal expression, let us introduce some notation. Recall first that the semantic theories we are concerned with are classes of structures \(\langle \mathcal {N}, (E, A)\rangle \), such that the anti-extension A can be defined via the extension E. And recall that for simplicity’s sake we have so far denoted these semantic theories as classes of structures \((\mathcal {N}, E)\), without explicit mention of the definable anti-extension A. It goes without saying that these semantic theories can equivalently be presented from the opposite perspective. That is, the semantic theories we are dealing with can be defined as classes of structures \(\langle \mathcal {N}, (E, A)\rangle \), such that E is definable via A. For example, in classical logic E can be defined as \(A^c\), i.e., as the complement of A, and in fixed-point models we can define E as \(E := \{ \varphi \in {\textsf {Sent}} \mid \lnot \varphi \in A \}\). So we can equivalently define semantic theories as classes of structures \((\mathcal {N}, A)\), without explicit mention of the definable extension E. For the purposes of this article, it is indeed sometimes convenient to conceive of models for \(\mathcal {L} _\mathrm {Tr} \) as structures \((\mathcal {N}, A)\) instead of \((\mathcal {N}, E)\). Hoping that our notation will not cause any confusion, we occasionally write

instead of

It is important to emphasise that there is no difference in the definition of the satisfaction relation  . That is to say,
. That is to say,  and
and  are just two notational variants expressing the same relation between structures \(\langle \mathbb {N}, (E, A)\rangle \) and sentences \(\varphi \). For example, in the case of a classical model \((\mathbb {N}, E)\) where E and A are disjoint and complementary, we do not define \((\mathbb {N}, A)\models \mathrm {Tr} (\varphi ) \text { iff } \varphi \in A\), but we understand it simply as a notational variant of the standard definition of the classical satisfaction relation, i.e., we have
are just two notational variants expressing the same relation between structures \(\langle \mathbb {N}, (E, A)\rangle \) and sentences \(\varphi \). For example, in the case of a classical model \((\mathbb {N}, E)\) where E and A are disjoint and complementary, we do not define \((\mathbb {N}, A)\models \mathrm {Tr} (\varphi ) \text { iff } \varphi \in A\), but we understand it simply as a notational variant of the standard definition of the classical satisfaction relation, i.e., we have
The reason for introducing this notational variant, as it will become clear in the following definition, is that it allows to express neatly the intuitive idea exposed above, according to which not only the class of the extensions of \(\mathrm {Tr}\), but also the class of its anti-extensions has to be sound and complete relative to \(\mathbb {N}\)-models of the semantic theory.
Criterion 9
(\(\mathbb {N}\)-categoricity\(^+\)) Let \(\mathrm {Th}\) be an axiomatic \(\mathcal {L} _\mathrm {Tr} \)-theory formulated in the logic L. Let X denote either E or A. Let  be the class of standard models of \(\mathrm {Th}\), and let \(\mathfrak {S} ^\mathbb {N}:=\{(\mathbb {N}, X)\mid (\mathbb {N}, X)\in \mathfrak {S} \}\) be the class of standard models of a semantic theory \(\mathfrak {S} \). \(\mathrm {Th}\) is an adequate axiomatisation of \(\mathfrak {S} \) if and only if,
be the class of standard models of \(\mathrm {Th}\), and let \(\mathfrak {S} ^\mathbb {N}:=\{(\mathbb {N}, X)\mid (\mathbb {N}, X)\in \mathfrak {S} \}\) be the class of standard models of a semantic theory \(\mathfrak {S} \). \(\mathrm {Th}\) is an adequate axiomatisation of \(\mathfrak {S} \) if and only if,

Intuitively, Criterion 9 imposes two requirements. First, it requires that a sentence \(\varphi \) is true in a \(\mathbb {N}\)-model of \(\mathrm {Th}\) precisely when this sentence is true in some \(\mathbb {N}\)-model in \(\mathfrak {S}\) (just as Criterion 2). Second, it requires that a sentence \(\varphi \) is untrue in a \(\mathbb {N}\)-model of \(\mathrm {Th}\) precisely when this sentence is untrue in some \(\mathbb {N}\)-model in \(\mathfrak {S}\).Footnote 21
3.3 Implementing the New Criteria
We conclude the first part of this article with two observations showing that the connection between the variants of KF and PKF studied by Halbach and Nicolai (2018) and Nicolai (2018) is fairly strong. To begin with, although it is not difficult to see that PKF (\(\textsf {PKF} _\textsf {S} \)) is an \(\mathbb {N}\)-categorical\(^+\) axiomatisation of the class of four-valued (symmetric) fixed-points of \(\Phi \), the same can be observed for the KF-variants as well, which is somewhat surprising.
Theorem 10
(i) KF and PKF are \(\mathbb {N}\)-categorical\(^+\) axiomatisations of the class of four-valued fixed-points of \(\Phi \). (ii) \(\textsf {KF} _\textsf {S} \) and \(\textsf {PKF} _\textsf {S} \) are \(\mathbb {N}\)-categorical\(^+\) axiomatisations of the class of symmetric fixed-points.
Second, having established that these variants of KF and PKF can be said to capture the Kripkean conception of truth equally well, we can compare them qua formal systems. It turns out that these theories not only agree on what is true, but they agree on what it untrue, too.
Proposition 11
Let \((\textsf {PKF} _\star , \textsf {KF} _\star )\) range over the following theory-pairs

Then
Detailed proofs of the last two observations are provided in the Appendix. Here we just sketch the proof idea.
Proof of idea of Theorem 10
Theorem 10 implies two different claims. The first, already known, is that E is the extension of \(\mathrm {Tr}\) in a \(\mathbb {N}\)-model of KF iff E is the extension of a fixed-point of \(\Phi \). The second claim is that A is the anti-extension of \(\mathrm {Tr}\) in \(\mathbb {N}\)-model of KF iff A is the anti-extension of a fixed-point of \(\Phi \). The second claim, in other words, means that

The left-to-right direction of this second claim can be shown by induction on the complexity of formulae: Given a model \((\mathbb {N}, A)\models \textsf {KF} \), one shows that, for \(E=\{\varphi \in {\textsf {Sent}} \mid \lnot \varphi \in A\}\),

which amounts to showing that \(\Phi (E,A)=(E,A)\). As for the right-to-left direction, one checks that, given a fixed point (E, A) of \(\Phi \), the structure \((\mathbb {N}, A)\) classically satisfies the axioms of KF. \(\square \)
Proof of idea of Proposition 11
The key to the proof is the fact that for any theory \(\mathrm {Th} \in \{\textsf {KF} _\star , \textsf {PKF} _\star \}\), we have
which in other words means \({\textsf {KF}} _\star ^A = {\textsf {KF}} _\star ^F\) and \({\textsf {KF}} _\star ^A={\textsf {PKF}} _\star ^F\). The equivalence stated in the Proposition now easily follows. We already know that \(\textsf {KF} _\star \) and \(\textsf {PKF} _\star \) agree on what is true, i.e., \({\textsf {KF}} _\star ^E={\textsf {PKF}} _\star ^E\). Since being false is understood as having a true negation, it follows that \({\textsf {KF}} _\star ^F={\textsf {PKF}} _\star ^F\). But since \({\textsf {KF}} _\star ^F= {\textsf {KF}} _\star ^A\) and \({\textsf {PKF}} _\star ^F = {\textsf {PKF}} _\star ^A\), we get \({\textsf {KF}} _\star ^A={\textsf {PKF}} _\star ^A\), and hence the desired conclusion \(\textsf {PKF} _\star ^\text{ ttc } =\textsf {KF} _\star ^\text{ ttc }\). \(\square \)
Let us conclude the first part of this article with a brief digression, mentioning a possible further refinement of the criteria just introduced. Criterion 9 requires that a sentence \(\varphi \) is true (untrue) in a standard model of \(\mathrm {Th}\) precisely when this sentence is true (untrue) in a standard model in \(\mathfrak {S}\). Definition 7 singles out the set of sentences which are provably (un)true in \(\mathrm {Th}\). In both cases, the focus is on truth-theoretic sentences. A referee, though, correctly pointed out that there is no reason why we should consider only truth-theoretic sentences and not truth-theoretic inferences as well. Indeed, a natural extension of both criteria, that would make them more broadly applicable, could be based on the inclusion of truth-theoretic inferences. Of course, there might be disagreement on what should count as a truth-theoretic inference, but the following seems to be a plausible option: Whereas a logical inference is a reasoning from a (possibly empty) set of premises \(\varphi , \psi , \xi \dots \) to a conclusion \(\sigma \), a truth-theoretic inference could be understood as a reasoning from a (possibly empty) set of premises \(\mathrm {Tr} (\varphi ), \mathrm {Tr} (\psi ), \mathrm {Tr} (\xi ) \dots \) to a conclusion \(\mathrm {Tr} (\sigma )\).Footnote 22
One way of extending Criterion 9, then, could consist in requiring that the internal logic (understood as provable truth-theoretic inferences) of a theory \(\mathrm {Th}\) be closed under the logic of the intended semantics. For example, suppose the intended semantics \(\mathfrak {S}\) is formulated over the logic L. Assume further that the inference from \(\varphi , \psi , \xi \dots \) to \(\sigma \) is an L-valid inference. Then one could argue that \(\mathrm {Th}\) captures \(\mathfrak {S}\) only if (in addition to being \(\mathbb {N}\)-categorical\(^+\)) \(\mathrm {Th}\) has enough resources to infer \(\mathrm {Tr} (\sigma )\) from the premises \(\mathrm {Tr} (\varphi ), \mathrm {Tr} (\psi ), \mathrm {Tr} (\xi ) \dots \).Footnote 23 Such an extension would overcome some inadequacies of Criteria 2 and 9.Footnote 24 Similarly, a more in depth comparison of two axiomatic systems (qua formal systems) could consist in investigating not only their respective truth-theoretic content (understood as provable truth-theoretic facts), but also their truth-theoretic logic (understood as their internal logic).Footnote 25 This would improve the analysis of the systems, as there are theories that prove the same truth-theoretic facts, but do not perform the same truth-theoretic reasoning.Footnote 26
4 Consistency and Completeness
The results presented in the previous section feed the philosophical doubts raised by Halbach and Nicolai vis-à-vis the use of nonclassical logic in this context, as we have seen that there is a stronger sense in which classical and nonclassical systems can be taken to be truth-theoretically equivalent.Footnote 27 So why should we axiomatise the fixed-point semantics using nonclassical logic, if we can obtain an equally good axiomatisation using classical logic? Why should we give up on sustained ordinary reasoning, and severely impede our inductive reasoning, if we can obtain the same truth-theoretic content working within a classical and powerful system?
It is indeed difficult to find a convincing answer to these questions. However, so far we have only considered some of the KF- and PKF-variants. Indeed, in the concluding remarks, Halbach and Nicolai point out that
[of] course, our results here are only a case study. The base theory can be varied, the assumptions on truth, and the way classical logic is restricted can be varied. In other base theories different schemata may be employed. We don’t intend to embark on the enterprise of browsing through all possible combinations. We think the burden of proof is with those who advocate a restriction of classical logic. (Halbach and Nicolai 2018, p. 251)
We now take the burden of proof, and we analyse two other variants of KF and PKF, namely variants restricting the class of models to consistent fixed-points, and variants restricting the class of models to complete fixed-points. It will turn out that for these variants different philosophical considerations are in order.Footnote 28
Let us label theories with consistency principles \(\textsf {KF} _\textsf {cs} \) and \(\textsf {PKF} _\textsf {cs} \), while theories with completeness principles \(\textsf {KF} _\textsf {cp} \) and \(\textsf {PKF} _\textsf {cp} \). \(\textsf {KF} _\textsf {cs} \) can be obtained from KF plus the axiom

(Cons) forces the truth predicate to be consistent: no sentence \(\varphi \) can be both true and false. Symmetrically, \(\textsf {KF} _\textsf {cp} \) can be obtained from KF plus the axiom

(Comp) forces the truth predicate to be complete: every sentence \(\varphi \) is either true or false.
As for the PKF-counterparts of these KF-variants, they have been introduced and investigated in Castaldo and Stern (2020).Footnote 29\(\textsf {PKF} _\textsf {cs} \) can be obtained from PKF plus an axiom schema imposing consistency, e.g.

Symmetrically, we can obtain the system \(\textsf {PKF} _\textsf {cp} \) from PKF plus an axiom schema imposing completeness, e.g.

Having defined (so to speak) the theories, let us see how they are related to each other. It is known that they are all \(\mathbb {N}\)-categorical axiomatisations of the intended class of fixed-points. Hence, relative to the \(\mathbb {N}\)-categoricity criterion, \(\textsf {KF} _\textsf {cs} \) and \(\textsf {PKF} _\textsf {cs} \) embody the consistent declination of the Kripkean conception of truth equally well. And similarly, \(\textsf {KF} _\textsf {cp} \) and \(\textsf {PKF} _\textsf {cp} \) capture the class of complete fixed-points equally well. Moreover, it has been shown that these pairs of theories prove the same sentence to be true:
Proposition 12
Let \((\textsf {PKF} _\star , \textsf {KF} _\star )\) range over the pairs
Then
Proof
This is a corollary of Proposition 4.15 of Castaldo and Stern (2020).Footnote 30\(\square \)
If we were now to employ the criteria presented in §2, we would have to say that, e.g., \(\textsf {KF} _\textsf {cs} \) and \(\textsf {PKF} _\textsf {cs} \) embody the consistent declination of the Kripkean conception of truth equally well, and we would have to say that they have the same truth-theoretic content.
However, even though it is easily observed that \(\textsf {PKF} _\textsf {cs} \) and \(\textsf {PKF} _\textsf {cp} \) are \(\mathbb {N}\)-categorical\(^+\) axiomatisations of the class of consistent, respectively complete, fixed-points, the same cannot be said for the consistent and complete versions of KF:
Observation 13
(i) \(\textsf {KF} _\textsf {cs} \) is not an \(\mathbb {N}\)-categorical\(^+\) axiomatisation of the class of consistent fixed-point models. (ii) \(\textsf {KF} _\textsf {cp} \) is not an \(\mathbb {N}\)-categorical\(^+\) axiomatisation of the class of complete fixed-point models.
Proof
(i) Let \(\tau \) be a Truth-teller. There are consistent fixed-points \((E_{\textsf {cs}}, A_\textsf {cs})\) of \(\Phi \), e.g. the least, such that \(\tau \wedge \lnot \tau \notin A_\textsf {cs}\), hence \((\mathbb {N}, A_\textsf {cs})\not \models \lnot \mathrm {Tr} (\tau \wedge \lnot \tau )\). However, \(\textsf {KF} _\textsf {cs} \vdash \lnot \mathrm {Tr} (\tau \wedge \lnot \tau )\), hence \((\mathbb {N}, A_\textsf {cs})\not \models \textsf {KF} _\textsf {cs} \). (ii) For \(\textsf {KF} _\textsf {cp} \), dual considerations hold. \(\square \)
Moreover, it is easy to see that neither \(\textsf {KF} _\textsf {cs} \)-and-\(\textsf {PKF} _\textsf {cs} \) nor \(\textsf {KF} _\textsf {cp} \)-and-\(\textsf {PKF} _\textsf {cp} \) agree on what is not-true.
Observation 14
For \((\textsf {PKF} _\star , \textsf {KF} _\star )\) as in Proposition 12,
Proof
There are many sentences that \(\textsf {KF} _\textsf {cs} \) deem not-true and that are independent from \(\textsf {PKF} _\textsf {cs} \). Dually, there are many sentences that \(\textsf {PKF} _\textsf {cp} \) deem not-true that are not so in \(\textsf {KF} _\textsf {cp} \). Again, the sentence \(\tau \wedge \lnot \tau \), for \(\tau \) a Truth-teller, is an example. \(\square \)
The asymmetry of \(\textsf {KF} _\textsf {cs} \) and \(\textsf {KF} _\textsf {cp} \) is stronger than the asymmetry of KF and \(\textsf {KF} _\textsf {S} \). One can say that KF and \(\textsf {KF} _\textsf {S} \) are weakly asymmetric, as they do not prove some of their theorems to be true. \(\textsf {KF} _\textsf {cs} \) and \(\textsf {KF} _\textsf {cp} \), however, are strongly asymmetric: the former, in fact, proves some of its theorems to be not-true, while the latter proves some of its theorems to be false. The example chosen more frequently involves a liar sentence \(\lambda \), and it is often pointed out that \(\textsf {KF} _\textsf {cs} \vdash \lambda \wedge \lnot \mathrm {Tr} (\lambda )\).Footnote 31 This strong asymmetry has been the target of a forceful criticism by several authors, such as Leon Horsten or Hartry Field. (Horsten 2011, p. 127), for example, emphasises that \(\textsf {KF} _\textsf {cs} \) “proves sentences that by its own lights are untrue” (emphasis in the original), and he takes this as a “sure mark of philosophical unsoundness.” (Field 2008, p. 132) additionally observes that \(\textsf {KF} _\textsf {cs} \) not only proves \(\varphi \wedge \lnot \mathrm {Tr} (\varphi )\) for certain degenerate sentences like Liars, but \(\textsf {KF} _\textsf {cs} \) proves instances of its own axioms to be untrue.Footnote 32 It seems undeniable that declaring some of its own theorems untrue, or false, is an odd feature of a truth system. And it seems—to use (Field 2008, p.132)’s words—“highly peculiar” to postulate an axiom schema, if one is then going to declare some of its instances untrue. In other words, being strongly asymmetric can be considered to be a problem per se.Footnote 33
That being said, however, this is not the claim defended in this paper. It will not be argued that declaring some of its own theorems and axioms untrue or false implies philosophical unsoundness. Let us reiterate on the fact that we are not comparing KF and PKF qua theories of truth simpliciter, in their own light. We are comparing them qua axiomatisations of the fixed-point semantics. In the next and last section we would thus like to focus on an additional and different problem of \(\textsf {KF} _\textsf {cs} \) and \(\textsf {KF} _\textsf {cp} \), which is in a sense a consequence of their strong asymmetry, and which is philosophically relevant for the present line of investigation on KF and PKF.
5 The Costs of Classical Logic
Have we shown that the class of consistent, respectively complete, fixed-points is captured more adequately by \(\textsf {PKF} _\textsf {cs} \) and \(\textsf {PKF} _\textsf {cp} \) rather than by \(\textsf {KF} _\textsf {cs} \) and \(\textsf {KF} _\textsf {cp} \)? What we have shown, so far, is that \(\textsf {KF} _\textsf {cs} \) and \(\textsf {KF} _\textsf {cp} \) are not \(\mathbb {N}\)-categorical\(^+\) axiomatisations of the consistent, respectively complete, fixed-point models. But this, it may be argued, is not enough to claim that, say, \(\textsf {KF} _\textsf {cs} \) does not embody the Kripkean conception of true in its consistent declination.Footnote 34 Establishing that the class of anti-extensions of \(\mathrm {Tr}\) in standard models of \(\textsf {KF} _\textsf {cs} \) is neither sound nor complete relative to the class of anti-extensions of \(\mathrm {Tr}\) in consistent fixed-point models is—one could argue—not necessarily a problem. In fact—the argument might continue—if a sentence \(\varphi \) is never in the extension of \(\mathrm {Tr}\) in consistent fixed-points, then there is a precise sense in which \(\varphi \) is not true. For example, classical contradictions, including those involving ungrounded sentences like Truth-tellers \(\tau \), are never in the extension of \(\mathrm {Tr}\), hence they might be taken to be not true. And so the fact that \(\textsf {KF} _\textsf {cs} \vdash \lnot \mathrm {Tr} (\tau \wedge \lnot \tau )\) but \(\textsf {PKF} _\textsf {cs} \not \vdash \lnot \mathrm {Tr} (\tau \wedge \lnot \tau )\) only shows that \(\textsf {KF} _\textsf {cs} \) is, but \(\textsf {PKF} _\textsf {cs} \) is not, able to capture this aspect of the consistent fixed-points semantics.
Let us suppose, for the sake of argument, that this line of reasoning justifying the provability of sentences such as \(\lnot \mathrm {Tr} (\tau \wedge \lnot \tau )\), on the ground that \(\tau \wedge \lnot \tau \) is never the extension on \(\mathrm {Tr}\), is indeed sound.Footnote 35 But even if one concedes that \(\textsf {KF} _\textsf {cs} \) captures the aspect of the consistent fixed-points semantics according to which, say, contradictions are not true, we do not believe that the same cannot be said for \(\textsf {PKF} _\textsf {cs} \). Indeed, we believe that \(\textsf {PKF} _\textsf {cs} \) does considerably better in this respect. It is in fact not difficult to see that we can distinguish between (in particular) two ways of being not true. The first is the one we have just introduced: There are sentences, like \(\tau \wedge \lnot \tau \), that are never true but not always untrue, i.e., sentences that are always outside the extension of \(\mathrm {Tr}\), however they are not always in its anti-extension. But there are also sentences, like \(0 + 0 \ne 0\), that are never true and always untrue, i.e., sentences that are always in the anti-extension of \(\mathrm {Tr}\). Now, \(\textsf {KF} _\textsf {cs} \) does not see the difference between these two ways of being something other than true, in the sense that \(\lnot \mathrm {Tr} (\tau \wedge \lnot \tau )\) and \(\lnot \mathrm {Tr} (0 + 0 \ne 0)\) are both theorems of \(\textsf {KF} _\textsf {cs} \):

By contrast, \(\textsf {PKF} _\textsf {cs} \) nicely captures this difference, as while \(\lnot \mathrm {Tr} (0 + 0 \ne 0)\) is a theorem of \(\textsf {PKF} _\textsf {cs} \), \(\mathrm {Tr} (\tau \wedge \lnot \tau )\) is only an antitheorem:

In other words, \(\textsf {PKF} _\textsf {cs} \) knows the difference between \(\tau \wedge \lnot \tau \) and \(0 + 0 \ne 0\): the former is never true, the latter is always untrue.Footnote 36
We would like to provide a final and crucial argument supporting the claim that \(\textsf {KF} _\textsf {cs} \) and \(\textsf {PKF} _\textsf {cs} \) cannot be taken to embody the Kripkean conception of truth equally well. Recall that in fixed-point models the anti-extension can be defined via the extension as follows:Footnote 37

The fact that A can be defined as the set of sentences whose negations are element of E, it should be observed, is not just a technical detail. As noted by (Soames 1999, p.181), “a guiding intuition behind Kripke’s formal construction is the idea that the status of the claim that a sentence S is true or that S is not true is dependent on the prior status of S or \(\lnot \)S.” This means that the status of \(\lnot \mathrm {Tr} (\varphi )\) depends on the status of \(\lnot \varphi \), upon which in turn depends the status of \(\mathrm {Tr} (\lnot \varphi )\). In other words, one of the distinctive features of the partial conception of truth presented by Kripke (1975) is that being not-true and being false are coextensive properties.
Crucially, Proposition 11 shows that this philosophical insight can be elegantly captured within a classical proof system. In fact, by inspecting the proof of Proposition 11, we realise that there exists a remarkable symmetry between semantics and proof theory: Extension and anti-extension induced by KF and \(\textsf {KF} _\textsf {S} \), and by PKF and \(\textsf {PKF} _\textsf {S} \), are related to each other in the exact same way as extension and anti-extension are related to each other in fixed-point models, that is

This is good news for the classical logician: the pleasing symmetry between semantics and proof theory can be preserved within classical systems. Yet, at the same time the costs of classical logic emerge precisely in the realisation that this symmetry is lost when we try to axiomatise consistent (or complete) fixed-point models within a classical system. It is here that we can see the impact of classical logic on what could be called ‘truth-theoretic reasoning’. In \(\textsf {KF} _\textsf {cs} \), the reasoning that leads us from \(\lnot \mathrm {Tr} (\varphi )\) to \(\mathrm {Tr} (\lnot \varphi )\) is no longer valid: If we know that a sentence is not-true, we cannot conclude that it is false. There is a precise sense, then, in which one can say that \(\textsf {PKF} _\textsf {cs} \) does, and \(\textsf {KF} _\textsf {cs} \) does not (at least, not as adequately as \(\textsf {PKF} _\textsf {cs} \)) capture the fixed-point semantics: Being not-true and being false are coextensive properties only in \(\textsf {PKF} _\textsf {cs} \), but not in \(\textsf {KF} _\textsf {cs} \), i.e.,

In sum, not only nonclassical logic, but also classical logic has its own costs: We cannot axiomatise the class of consistent (or complete) fixed-points in classical logic as adequately as we can do within a nonclassical system. Having established that both frameworks have their own virtues and their own costs, a natural further step in this investigation would consist in assessing which option is best. The nonclassical logician should reflect on whether the cost of losing proof-theoretic strength surpasses the virtue of having a transparent truth predicate. The classical logician should reflect on whether the possibility of using ordinary reasoning is enough to justify the loss of some insights of the intended semantics. These questions will not be discussed here.
Let us conclude by providing a response to Halbach and Nicolai’s warning, according to which “the incision [of nonclassical logic] doesn’t hit our truth-theoretic reasoning; it hits mathematical reasoning at its heart” (Halbach and Nicolai 2018, p. 229). Whereas the mathematical costs of nonclassical logic can be quantified as the transfinite distance between \(\omega ^\omega \) and \(\varepsilon _0\), the truth-theoretic costs of classical logic can be identified with the impossibility of reasoning about truth in the intended way. In response, or better: in addition, to Halbach and Nicolai’s warning, it may then be held that the incision of classical logic doesn’t hit our mathematical reasoning; it hits our truth-theoretic reasoning at its heart.
Notes
The theory KF was devised by Feferman (see Feferman (1991)) and further studied by, e.g., (Reinhardt 1986; Cantini 1989; McGee 1990). The theory PKF may be seen as the nonclassical counterpart to KF. It was introduced by Halbach and Horsten (2006) and further studied by, e.g., (Fischer and Gratzl 2018; Halbach and Nicolai 2018; Nicolai 2018).
The depth of these consequences can be characterised precisely: KF proves the schema of transfinite induction up to any ordinal smaller than \(\varepsilon _0\), PKF proves the same schema only up to any ordinal smaller than \(\omega ^\omega \). The ordinal \(\varepsilon _0\) is defined as \(\sup \{\omega , \omega ^\omega , \omega ^{\omega ^\omega }, \dots \} = \) least \(\alpha \) such that \(\omega ^\alpha =\alpha \).
A project recently carried out by Field (2020) is worth mentioning: Field has shown that one can recover, in PKF, the full proof-theoretic strength of KF by adding a predicate of “strong classicality”. A similar strategy had already been investigated by Picollo (2018). Picollo defines a variant of PKF, called CKF, in a logic of formal inconsistency extending LP (the Logic of Paradox, introduced by Priest (1979)) with a consistency operator. She shows, however, that this is not enough to obtain a system as strong as KF.
Below we will see that some KF-variants are such that, for some \(\varphi \), they prove \(\varphi \) and \(\lnot \mathrm {Tr} (\varphi )\). As (Halbach and Horsten 2006, p. 682) put it, these variants “disprove [their] own soundness”.
The various induction schemata are defined in the Appendix.
The systems \(\textsf {PKF} ^+\) and \(\textsf {PKF} _\textsf {S} ^+\) were first introduced by Nicolai (2018). Let us recall that transfinite induction up to any ordinal below \(\varepsilon _0\) is derivable in KF.
This is not the only possible reading of Kripke’s construction. As suggested by (Kripke 1975, p. 715) himself, his construction can capture two different intuitions. The first is the one we are investigating here, according to which a sentence \(\varphi \) has the same semantic value as the sentence \(\mathrm {Tr} (\varphi )\), and consequently \(\mathrm {Tr} (\varphi )\) suffers a truth-value gap whenever \(\varphi \) does. A second intuition is that a sentence which is either false or undefined is not true. On this view, the truth predicate would be classical and not allow any truth-value gaps. To accommodate this intuition, one can obtain classical models by “closing off” the fixed-points, i.e., one declares false every sentence that did not receive a truth-value in the construction of the fixed-point. We thank a referee for pointing out the need of clarifying this point.
It should be also be noted that we are not considering fixed-points obtained by means of a (non-compositional) supervaluation scheme, where a disjuction can be true without it following that some disjunct is true. For more details on supervaluations and Kripkean truth, see e.g. Kremer and Urquhart (2008) and Stern (2018).
The following formulation is due to Halbach and Nicolai (2018)—although we have opted for a slightly different presentation—and it differs from the original definition of Fischer et al. (2015). The latter was thought for classical theories. Fischer et al. (2015) then adapt the criterion to a nonclassical setting, but only for the Kripkean fixed-point semantics, and only for systems formulated in the same logic as that of the semantics (see (Fischer et al. 2015, §4.3)).
Halbach and Nicolai (2018) remark that the same holds for \(\textsf {KF} _\textsf {S} \) and \(\textsf {PKF} _\textsf {S} \), i.e., they are \(\mathbb {N}\)-categorical axiomatisations of the class of symmetric fixed-points.
One of these is mentioned by Halbach and Nicolai (2018), in footnote 6: Replacing the truth-theoretic initial sequents of PKF with the initial sequents \(\varphi \Rightarrow \mathrm {Tr} (\varphi )\) and \(\mathrm {Tr} (\varphi )\Rightarrow \varphi \) yields an \(\mathbb {N}\)-categorical axiomatisation of the FDE-fixed points. For a more general discussion of the \(\mathbb {N}\)-categority criterion and some possible alternatives, see Fischer et al. (2015).
Not every classical tautology is provable in PKF, hence it cannot contain any classical theory.
Incidentally, an answer to this question not only determines how KF and PKF are related in terms of what they prove to be true, but it also yields a comparison between their truth-free consequences, as both kinds of theory prove Tarski-biconditionals for all \(\varphi \in \mathcal {L}_{\textsf {PA} } \).
As mentioned, the systems \(\textsf {PKF} ^+\) and \(\textsf {PKF} _\textsf {S} ^+\) were first introduced by Nicolai (2018), where he showed that they contain the internal theories of KF and \(\textsf {KF} _\textsf {S} \), respectively. Due to Nicolai (2018) is also the proof of the inclusions \(\textsf {KF} ^\textsf {int} \subseteq \textsf {PKF} \) and \(\textsf {KF} ^\mathsf int _\textsf {S} \subseteq \textsf {PKF} _\textsf {S} \).
Note that KF and \(\textsf {KF} _\textsf {S} \) (and hence KF and \(\textsf {PKF} _\textsf {S} \)) prove the same sentences to be true, but they can hardly be said to embody the same conception of truth.
We use ‘not-true’ as synonymous with untrue.
We thank a referee for suggesting this possible objection.
\(\mathrm {Th} ^F\) can be defined via \(\mathrm {Th} ^E\), i.e., \(\mathrm {Th} ^F := \{\varphi \mid \lnot \varphi \in \mathrm {Th} ^E\}\).
Of course we are not suggesting (nor this was the suggestion by Halbach and Nicolai (2018) relative to the notion of inner theory) that the one below is the definition of truth-theoretic content of a theory \(\mathrm {Th}\), assuming that such a definition be possible at all. Actually, we believe that the definition below is far from being comprehensive for a thorough comparison of conceptual aspects of two formal systems. We shall say more on this below.
Let us emphasise, straight away, that Criterion 9 is meant to be only an improvement of Criterion 2. In general terms, it is still an approximation and it can be seen only as a necessary condition to impose on axiomatic systems. Just to mention a issue similar to one pointed at in footnote 11: Replacing the initial sequents of PKF with the initial sequents \(\varphi \Leftrightarrow \mathrm {Tr} (\varphi )\) and \(\lnot \varphi \Leftrightarrow \lnot \mathrm {Tr} (\varphi )\) yields an \(\mathbb {N}\)-categorical\(^+\) axiomatisation of the FDE-fixed points. For a more in depth study of the implications of reflecting on the truth-theory with truth initial sequents \(\varphi \Leftrightarrow \mathrm {Tr} (\varphi )\) and \(\lnot \varphi \Leftrightarrow \lnot \mathrm {Tr} (\varphi )\), see Fischer et al. (2017).
Let us remark that Castaldo and Stern (2020) have shown that all pairs of KF- and PKF-like theories studied here are such that they contain theories proving the same truth-theoretic inferences, which is why we have opted for the simpler definitions focusing only on sentences.
Formally, this amounts to requiring that a set of complete rules for L are ‘internally derivable’ in \(\mathrm {Th}\). More precisely, let S be a (say, sequent) calculus which is sound and complete relative to L. Then the requirement would be that for any rule \(\frac{\Gamma _1\Rightarrow \Delta _1 \ \dots \ \Gamma _n\Rightarrow \Delta _n}{\Gamma \Rightarrow \Delta }\) of S, the rule \(\frac{\mathrm {Tr} (\Gamma _1)\Rightarrow \mathrm {Tr} (\Delta _1) \ \dots \ \mathrm {Tr} (\Gamma _n)\Rightarrow \mathrm {Tr} (\Delta _n)}{\mathrm {Tr} (\Gamma )\Rightarrow \mathrm {Tr} (\Delta )}\) is derivable in \(\mathrm {Th}\), where for a set of sentences \(\Theta \), \(\mathrm {Tr} (\Theta ):=\{\mathrm {Tr} (\theta )\mid \theta \in \Theta \}\).
In particular, the internal logic of the theory mentioned above with initial sequents \(\mathrm {Tr} (\varphi )\Leftrightarrow \varphi \) and \(\lnot \varphi \Leftrightarrow \lnot \mathrm {Tr} (\varphi )\) is not closed under FDE. For instance, the sequent \(\mathrm {Tr} (\forall x\varphi (x))\Rightarrow \mathrm {Tr} (\varphi (y))\), where \(\varphi (y)\) is a formula with y free is not derivable for all \(\varphi (y)\).
Formally, the truth-theoretic logic of a theory \(\mathrm {Th}\) could be defined as the set of pairs \(\langle {\Gamma ,\Delta }\rangle \) of sets of sentences, such that \(\mathrm {Th} \vdash \mathrm {Tr} (\Gamma )\Rightarrow \mathrm {Tr} (\Delta )\).
For example, KF and \(\textsf {KF} _\textsf {S} \) (although they do not capture the same semantics) prove the same sentences to be true and the same sentences to be untrue, yet they are different reasoning apparati about truth. In particular, the reasoning “if \(\varphi \) is both true and false, then any sentence \(\psi \) is either true or false” is licensed in \(\textsf {KF} _\textsf {S} \), but not in KF.
Let us reiterate on a point already emphasised at the end of §2. The claim that these variants of KF and PKF can be taken to embody the same conception of truth is a consequence of their being \(\mathbb {N}\)-categorical\(^+\) axiomatisations of the relevant class of fixed-point models. The claim that, qua formal systems, they are truth-theoretically equivalent is a consequence of their having the same truth-theoretic content.
It goes without saying that also the present results are only a case study. In particular, we are analysing variants of KF and PKF only over PA, and it is not known whether the same considerations hold if we modify the base theory. What is known, is that proof-theoretic results about systems formulated over PA are not preserved if we move to a set-theoretic framework: Fujimoto (2018) has shown that KF and Cantini’s VF (see Cantini 1990) are proof-theoretically equivalent over set theory ZF, that is, they have the same set-theoretic consequences. Over PA, however, VF is significantly stronger than KF.
As already mentioned, Picollo (2018) defines a similar PKF-like system as a counterpart of \(\textsf {KF} _\textsf {cp} \).
It should be noted that the proofs of Propositions 2 and 3 of Nicolai (2018), showing that I \(\textsf {KF} ^\textsf {int} \) and KF are contained in PKF and \(\textsf {PKF} ^+\), respectively, de facto also show that I \(\textsf {KF} ^\mathsf int _\textsf {cs} \) and I \(\textsf {KF} _\textsf {cs} \) are contained, respectively, in \(\textsf {PKF} _\textsf {cs} \) and \(\textsf {PKF} _\textsf {cs} ^+\).
Dually, \(\textsf {KF} _\textsf {cp} \vdash \lnot \lambda \wedge \mathrm {Tr} (\lambda )\).
Field (2008) formulates \(\textsf {KF} _\textsf {cs} \) as KF with the additional axiom often called \(\mathrm {Tr}\)-Out, i.e. \(\mathrm {Tr} (\varphi )\rightarrow \varphi \). It can be shown that, e.g., \(\textsf {KF} _\textsf {cs} \vdash \lnot \mathrm {Tr} (\mathrm {Tr} (\lambda )\rightarrow \lambda )\), for \(\lambda \) a liar sentence.
For a defence of \(\textsf {KF} _\textsf {cs} \) against the charge of proving some its theorems to be untrue, see in particular Maudlin (2004).
In these concluding remarks, we concentrate on the pair (\(\textsf {KF} _\textsf {cs} \), \(\textsf {PKF} _\textsf {cs} \)), but dual considerations hold for the pair (\(\textsf {KF} _\textsf {cp} \), \(\textsf {PKF} _\textsf {cp} \)).
Whether this argument is tenable, though, is not obvious. If one follows this line of reasoning, then one should say that, if a sentence \(\varphi \) is never in the anti-extension of \(\mathrm {Tr}\) in consistent fixed-point models, then \(\varphi \) is not untrue. For example, one should say that sentences like \(\tau \vee \lnot \tau \) or \(\lambda \), since they are never in the anti-extension of \(\mathrm {Tr}\) in consistent fixed-points, they are not untrue. However, not only e.g. \(\textsf {KF} _\textsf {cs} \not \vdash \lnot \lnot \mathrm {Tr} (\tau \vee \lnot \tau )\), but we even have \(\textsf {KF} _\textsf {cs} \vdash \lnot \mathrm {Tr} (\lambda )\). So it is not clear whether one can justify the provability of \(\lnot \mathrm {Tr} (\tau \wedge \lnot \tau )\) by noting that \(\tau \wedge \lnot \tau \) is never in the extension of \(\mathrm {Tr}\).
Borrowing Field (2008)’s terminology, one could say that sentences like \(0 + 0 \ne 0\) are determinately untrue, whereas sentences like \(\tau \wedge \lnot \tau \) are not determinately true. (Field 2008, §3.6) also argues that a weakness of a system akin to PKF (that he calls \(\textsf {KF} \textsf {S} \)) is that it has no way of expressing that sentences like \(\tau \wedge \lnot \tau \) (or Liar sentences) are not determinately true, because no weak negation can be introduced within the system. Pace Field, it seems to us that anti-theorems are a very neat way of expressing the non determinate truth of such sentences.
We drop \(\textsf {NSent} \) for readability.
(RepL) and (RepR) are equivalent over FDE, and they both yield the replacement schema
$$s = t, \varphi (s), \Gamma \Rightarrow \Delta , \varphi (t).$$The reason for formulating \(\textsf {K} \mathsf {3} _=\) and \(\textsf {KS} \mathsf {3} _=\) with (RepL), and LP with (RepR) is to obtain a syntactic proof of full Cut elimination. See Castaldo and Stern (2020) for details.
Regularity axioms were dropped in Feferman’s formulation of KF since they are derivable by (IND). They were introduced by Cantini (1989) since they are not derivable in systems without full induction for \(\mathcal {L} _\mathrm {Tr} \).
Castaldo and Stern (2020) define KF and PKF variants using rules of inference instead of axioms, in order to simply the arguments of some proof-theoretic results. But the systems can be shown to be equivalent.
Adding \(\lnot \Delta \Rightarrow \lnot \Gamma \) for \(\Gamma \Rightarrow \Delta \) axiom of PA to \(\textsf {PKF} \)-like theories makes contraposition admissible in PKF and \(\textsf {PKF} _\textsf {S} \).
Note that
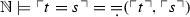 .
.
References
Blamey, Stephen (2002). Partial logic. In Handbook of philosophical logic (Dov M. Gabbay and Franz Günthner, eds.), pages 261–353. Springer, Berlin
Cantini, Andrea. (1989). Notes on formal theories of truth. Mathematical Logic Quarterly, 35(2), 97–130.
Cantini, Andrea (1990). A theory of formal truth arithmetically equivalent to ID1. Journal of Symbolic Logic, 244–259.
Castaldo, Luca, & Stern, Johannes (May 2020). KF, PKF, and Reinhardt’s program. arXiv e-prints, page arXiv:2005.01054.
Feferman, Solomon. (1968). Systems of predicative analysis, II: Representations of ordinals. The Journal of Symbolic Logic, 33(2), 193–220.
Feferman, Solomon. (1984). Toward useful type-free theories I. The Journal of Symbolic Logic, 49(1), 75–111.
Feferman, Solomon. (1991). Reflecting on incompleteness. The Journal of Symbolic Logic, 56(1), 1–49.
Fischer, Martin, & Gratzl, Norbert. (2018). Truth, partial logic and infinitary proof systems. Studia Logica, 106(3), 515–540.
Fischer, Martin, Halbach, Volker, Kriener, Jönne, & Stern, Johannes. (2015). Axiomatizing semantic theories of truth? The Review of Symbolic Logic, 8(2), 257–278.
Field, Hartry. (2008). Saving truth from paradox. Oxford: Oxford University Press.
Field, Hartry. (2020). The power of naive truth. The Review of Symbolic Logic, page, 1–34.
Fischer, Martin, Nicolai, Carlo, & Horsten, Leon. (2017). Iterated reflection over full disquotational truth. Journal of Logic and Computation, 27(8), 2631–2651.
Fujimoto, Kentaro. (2010). Relative truth definability of axiomatic truth theories. Bulletin of symbolic logic, 16(3), 305–344.
Fujimoto, Kentaro. (2018). Truths, inductive definitions, and Kripke-Platek systems over set theory. The Journal of Symbolic Logic, 83(3), 868–898.
Halbach, Volker. (2014). Axiomatic theories of truth. Cambridge: Second ed. Cambridge University Press.
Halbach, Volker, & Horsten, Leon. (2006). Axiomatizing Kripke’s theory of truth. The Journal of Symbolic Logic, 71(2), 677–712.
Halbach, Volker, & Nicolai, Carlo. (2018). On the costs of nonclassical logic. Journal of Philosophical Logic, 47(2), 227–257.
Horsten, Leon. (2009). Levity. Mind, 118(471), 555–581.
Horsten, Leon (2011). The Tarskian turn: Deflationism and axiomatic truth. Mit Press.
Kripke, Saul. (1975). Outline of a theory of truth. The Journal of Philosophy, 72(19), 690–716.
Kremer, Philip, & Urquhart, Alasdair. (2008). Supervaluation fixed-point logics of truth. Journal of Philosophical Logic, 37(5), 407–440.
Maudlin, Tim (2004). Truth and paradox: Solving the riddles. Oxford University Press.
McGee, Vann (1990). Truth, vagueness, and paradox: An essay on the logic of truth. Hackett Publishing.
Nicolai, Carlo. (2018). Provably true sentences across axiomatizations of Kripke’s theory of truth. Studia Logica, 106(1), 101–130.
Picollo, Lavinia. (2018). Truth in a logic of formal inconsistency: How classical can it get? Logic Journal of the IGPL, 28(5), 771–806.
Pohlers, Wolfram. (2009). Proof theory: The first step into impredicativity. Springer Science & Business Media.
Priest, Graham. (1979). The logic of paradox. Journal of Philosophical Logic, 8(1), 219–241.
Reinhardt, William N. (1985). Remarks on significance and meaningful applicability. Mathematical Logic and Formal Systems, 94, 227–242.
Reinhardt, William N. (1986). Some remarks on extending and interpreting theories with a partial predicate for truth. Journal of Philosophical Logic, 15(2), 219–251.
Scott, Dana. (1975). Combinators and classes. In Böhm C. (eds), International Symposium on Lambda-Calculus and Computer Science Theory, pages 1–26. Springer
Soames, Scott. (1999). Understanding truth. Oxford University Press.
Stern, Johannes. (2018). Supervaluation-style truth without supervaluations. Journal of Philosophical Logic, 47(5), 817–850.
Troelstra, Anne Sjerp, & Schwichtenberg, Helmut (2000). Basic proof theory. Second ed. Cambridge University Press.
Takeuti, Gaisi (1987). Proof theory. Second ed. Studies in Logic and the Foundations of Mathematics, vol. 81. Elsevier Science Publishers.
Acknowledgements
I wish to thank audiences of the FSB seminar in Bristol and of the Axiomatizing Metatheory Workshop in Salzburg for their remarks, in particular I thank Catrin Campbell-Moore, Volker Halbach, and Carlo Nicolai. I thank two anonymous referees for their pertinent and helpful comments. I am particularly grateful to Leon Horsten and Johannes Stern for discussing with me the ideas of this paper on several occasions, and for their detailed and valuable suggestions. This work has been supported by the AHRC South, West and Wales Doctoral Training Partnership (SWW DTP), Grant No. AH/L503939/1-DTP1.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
In this appendix we provide technical details about the results mentioned in the paper. In particular, we prove Theorem 10 and Proposition 11.
Language and notation \(\mathcal {L} _\mathrm {Tr} \) denotes the language of first-order Peano arithmetic (PA), specified by the signature \(\{0, ', +, \times \}\), extended by a unary predicate \(\mathrm {Tr}\). \(\mathcal {L}_{\textsf {PA} }:=\mathcal {L} _\mathrm {Tr} \backslash \{T\}\) is the \(\mathrm {Tr}\)-free fragment of \(\mathcal {L} _\mathrm {Tr} \). Terms and formulae are generated in the usual way (i.e., from atoms by closing off under \(\lnot ,\wedge ,\forall \), the other symbols being defined according to classical logic). By an \(\mathcal {L} _\mathrm {Tr} \)-expression we mean a term or a formula of \(\mathcal {L} _\mathrm {Tr} \). We denote by \(\mathsf {n}\) the numeral corresponding to the number \(n\in \omega \). We fix a canonical Gödel numbering of \(\mathcal {L} _\mathrm {Tr} \)-expressions. If e is an \(\mathcal {L} _\mathrm {Tr} \)-expression, the Gödel number (= gn) of e is denoted by \(\#e\) and \(\ulcorner {e}\urcorner \) is the term representing \(\#e\) in \(\mathcal {L}_{\textsf {PA} } \). The sets of codes of terms, closed terms, variables, formulae, and sentences are primitive recursive and can be represented in PA. We introduce some primitive recursive relations, understood as abbreviations for equations involving the (primitive recursive) characteristic function for these sets:

We also assume to have standard representations of the following primitive recursive operations on Gödel numbers:

The expression \(e[t/v_k]\) is the result of replacing, in the expression e, each free occurrence of \(v_k\) by the term t. We adopt the following abbreviations:

We occasionally write x(t), when it is clear which variable is being substituted. Our language also features a recursive evaluation function \({\textsf {val}} (x)\) such that \({\textsf {val}} (\ulcorner {t}\urcorner ) = t\) for closed terms t.
A sequent is a pair \(\Gamma \Rightarrow \Delta \) of finite sets of \(\mathcal {L} _\mathrm {Tr} \)-formulae. A derivation of a sequent \(\Gamma \Rightarrow \Delta \) is a tree with nodes labelled by sequents (for details, the reader is referred to Troelstra and Schwichtenberg 2000). A literal is an atomic formula or the negation of an atomic formula.
Logic: Semantics and Sequent Calculi
In this section we introduce the various logics underlying the systems of truth employed in the paper. The sequent calculi are defined as in Castaldo and Stern (2020). We start with the two-sided sequent calculus First Degree Entailment (FDE).
Definition 1
(FDE) FDE consists of the following axioms and rules.

Conditions of application: \(\varphi \) literal in initial sequents; u eigenparameter; t arbitrary term.
Let

Definition 15
-
Classical Logic, CL, is the system given by FDE without \(\lnot \circ M\), for \(\circ \in \{\lnot , \wedge , \forall \}, M\in \{\text {L, R}\}\), and with the addition of (\(\lnot \)L) and (\(\lnot \)R).
-
Strong Kleene, \(\textsf {K} \mathsf {3}\), is the system FDE plus the rule (\(\lnot \)L) restricted on \(\varphi \) atomic sentence.
-
Logic of Paradox, LP, is the system FDE plus the rule (\(\lnot \)R) restricted on \(\varphi \) atomic sentence.
-
Kleene’s Symmetric Logic, \(\textsf {KS} \mathsf {3}\), is the system FDE plus the rule \((\textsf {GG} )\) restricted on \(\varphi \) atomic sentence.Footnote 38
Using Cut, it can be shown that the rules (\(\lnot \)L), (\(\lnot \)R), and (GG), are derivable in, respectively, \(\textsf {K} \mathsf {3}\), LP, and \(\textsf {KS} \mathsf {3}\), for all formulae. We now extend the base logics with rules for identity. Let

for \(\varphi \) literal.
Definition 16
-
\(\textsf {CL} _{=}\) is CL \(+\) (Ref) \(+\) (RepL).
-
\(\textsf {FDE} _{=}\) is FDE \(+\) (Ref) \(+\) (RepL).
-
\(\textsf {K} \mathsf {3} _{=}\) is \(\textsf {K} \mathsf {3}\) \(+\) (Ref) \(+\) (RepL).
-
\(\textsf {LP} _{=}\) is LP \(+\) (Ref) \(+\) (RepR).
-
\(\textsf {KS} \mathsf {3} _{=}\) is \(\textsf {KS} \mathsf {3}\) \(+\) (Ref) \(+\) (RepL).Footnote 39
Definition 17
A four-valued model for \(\mathcal {L} _\mathrm {Tr} \) is a structure \(\langle \mathcal {N}, (E, A)\rangle \) such that \(\mathcal {N}\) is a model for \(\mathcal {L}_{\textsf {PA} }\) and \((E, A)\in \wp (|{\mathcal {N}}|)^2\) is a pair of subsets of \(|{\mathcal {N}}|\) (the support of \(\mathcal {N}\)). A four valued model is
-
consistent, or \(\textsf {K} \mathsf {3}\), if \(E \cap A = \varnothing \),
-
complete, or LP, if \(E \cup A = |{\mathcal {N}}|\),
-
symmetric, or \(\textsf {KS} \mathsf {3}\), if it is either consistent or complete,
-
mixed, if it not symmetric.
Definition 18
Let: \(\mathcal {L} _\mathrm {Tr} (\mathcal {N})\) denote \(\mathcal {L} _\mathrm {Tr} \) expanded by distinct constants \(\mathsf {a, b, c}, \dots \) for distinct elements a, b, c, ...\(\in \mathcal {N}\); \(\mathcal {M}:=\langle \mathcal {N}, (E, A)\rangle \) be a four-valued model; s, t be closed terms of \(\mathcal {L} _\mathrm {Tr} (\mathcal {N})\); \(\varphi , \psi \) be \(\mathcal {L} _\mathrm {Tr} (\mathcal {N})\)-sentences; \(\chi (v)\) a formula with at most v free; \(t^\mathcal {M} \) be the value of t in \(\mathcal {M}\). Then

Definition 19
The relation  is extended to sequents as follows:
is extended to sequents as follows:  iff
iff
-
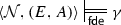 , for all \(\gamma \in \Gamma \), then
, for all \(\gamma \in \Gamma \), then 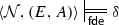 for some \(\delta \in \Delta \).
for some \(\delta \in \Delta \).
KF- and PKF-variants
Given a standard notation system of ordinals up to \(\Gamma _0\),Footnote 40 we use \(a, b, c \dots \) to denote the code of our notation system whose value is \(\alpha , \beta , \gamma \dots \in On\) (with the exception of \(\omega \) and \(\varepsilon \)-numbers, for which we use the ordinals themselves). We use \(\prec \) to denote a primitive recursive ordering defined on codes of ordinals. For \(\alpha <\Gamma _0\) and a formula \(\varphi (v)\in \mathcal {L} _\mathrm {Tr} \) we let \(\textsf {TI} ^{<\alpha }(\varphi )\) denote

We have the following induction schemata (\(\varphi (v)\in \mathcal {L} _\mathrm {Tr} \)):


where u is an eigenvariable and z is an arbitrary term.
Definition 20
(Truth Axioms) The following truth-theoretic initial sequents are called truth axioms. Reg1-2 are called regularity axioms.Footnote 41

\(\dot{\textsf {val} (y)} := \textsf {num} (\textsf {val} (y))\)
Definition 21
(KF) KF is obtained from \(\textsf {CL} _=\) by adding sequents \(\Gamma \Rightarrow \Delta \) for \(\Gamma \Rightarrow \Delta \) axiom of PA, (see e.g. Takeuti 1987) (IND), and all truth axioms of Df. 20 except \((\lnot \mathrm {Tr} \lnot )\).
We now define KF and PKF variants.Footnote 42
Definition 22
(KF-variants)
-
(i)
\(\textsf {KF} _\textsf {cs} \) is obtained from KF by adding Cons, i.e.,
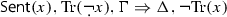 .
. -
(ii)
\(\textsf {KF} _\textsf {cp} \) is obtained from KF by adding Comp, i.e.,
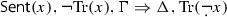 .
. -
(iii)
\(\textsf {KF} _\textsf {S} \) is obtained from KF by adding
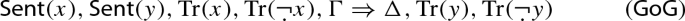
For \(\mathrm {Th}\in \{\textsf {KF} , \textsf {KF} _\textsf {cs} , \textsf {KF} _\textsf {cp} , \textsf {KF} _\textsf {S} \}\),
-
(iv)
\(\mathrm {Th}^- \) is obtained from \(\mathrm {Th}\) by restricting (IND) on \(\mathcal {L}_{\textsf {PA} } \)-formulae.
-
(v)
\(\mathrm {Th}^\mathsf{int }\) is the theory obtained from \(\mathrm {Th}^- \) by replacing the restricted version of (IND) with \((\mathsf {IND} ^\mathsf {int} )\).
Definition 23
(PKF) PKF is obtained from \(\textsf {FDE} _=\) by adding sequents \(\Gamma \Rightarrow \Delta \) and \(\lnot \Delta \Rightarrow \lnot \Gamma \) for \(\Gamma \Rightarrow \Delta \) axiom of PA, (IND), truth axioms of Df. 20, and the following two rules requiring identity statements to behave classically:Footnote 43

Definition 24
(PKF-cluster)
-
(i)
\(\textsf {PKF} _\textsf {cs} \) is obtained by adding (\(\lnot \)L) to PKF.
-
(ii)
\(\textsf {PKF} _\textsf {cp} \) is obtained by adding (\(\lnot \)R) to PKF.
-
(iii)
\(\textsf {PKF} _\textsf {S} \) is obtained by adding (GG) to PKF.
For \(\mathrm {Th}\in \{\textsf {PKF} , \textsf {PKF} _\textsf {cs} , \textsf {PKF} _\textsf {cp} , \textsf {PKF} _\textsf {S} \}\),
-
(iv)
\(\mathrm {Th}^- \) is obtained from \(\mathrm {Th}\) by restricting (IND) on \(\mathcal {L}_{\textsf {PA} } \)-formulae.
-
(v)
\(\mathrm {Th}^+\) is obtained by extending \(\mathrm {Th}\) with \((\textsf {TI} ^{<\varepsilon _0})\).
An important property of PKF and \(\textsf {PKF} _\textsf {S} \) is that they admit the rule of contraposition.
Lemma 25
(Castaldo and Stern 2020) Contraposition, i.e. the rule
is admissible in PKF and \(\textsf {PKF} _\textsf {S} \).
Proof
See (Castaldo and Stern 2020, Lemma 3.11) \(\square \)
Proofs
In this section we prove the two main results, being sloppy about notation. In particular, we don’t distinguish between a sentence \(\varphi \) and its code \(\#\varphi \) when there is no danger of confusion.
Proof of Theorem 10
Let

We want to show two claims:
-
(i)
\((\mathbb {N}, E)\models \textsf {KF} \) iff \(\Phi (E, A)=(E, A)\), for \(A:=\{\varphi \in {\textsf {Sent}} \mid \lnot \varphi \in E\}\cup \textsf {NSent}\);
-
(ii)
\((\mathbb {N}, A)\models \textsf {KF} \) iff \(\Phi (E, A)=(E, A)\), for \(E:=\{\varphi \in {\textsf {Sent}} \mid \lnot \varphi \in A\}\).
Condition (i) is already known to be satisfied. We prove (ii). We begin by showing that
If \((\mathbb {N}, A)\models \textsf {KF} \), then \(\Phi (E, A)=(E, A)\).
Let \((\mathbb {N}, A)\models \textsf {KF} \). We first show that, for \(E:=\{\varphi \in \textsf {Sent} \mid \lnot \varphi \in A\}\),
 This amounts to showing that, for all sentences \(\varphi \in \mathcal {L} _\mathrm {Tr} \),
This amounts to showing that, for all sentences \(\varphi \in \mathcal {L} _\mathrm {Tr} \),

The proof is by induction on \(\varphi \).
 \(\varphi \in \mathcal {L}_{\textsf {PA} } \) Being a model of KF, \((\mathbb {N}, A)\models \mathrm {Tr} \ulcorner {\varphi }\urcorner \leftrightarrow \varphi \).
\(\varphi \in \mathcal {L}_{\textsf {PA} } \) Being a model of KF, \((\mathbb {N}, A)\models \mathrm {Tr} \ulcorner {\varphi }\urcorner \leftrightarrow \varphi \).
 \(\varphi \equiv \mathrm {Tr} (t)\) Note that
\(\varphi \equiv \mathrm {Tr} (t)\) Note that  iff \(\mathrm {Tr} (t)\in E\) iff (by definition of E) \(\mathrm {Tr} (t)\) is a sentence such that \(\lnot \mathrm {Tr} (t)\in A\), iff
iff \(\mathrm {Tr} (t)\in E\) iff (by definition of E) \(\mathrm {Tr} (t)\) is a sentence such that \(\lnot \mathrm {Tr} (t)\in A\), iff
iff (since \((\mathbb {N}, A)\) is a model of the axiom \((\mathrm {Tr} \lnot \mathrm {Tr})\)) \(\mathbb {N} \models {\textsf {Sent}} ({\textsf {val}} (\ulcorner {t}\urcorner ))\) and  . Let \({\textsf {val}} (\ulcorner {t}\urcorner )=\ulcorner {\psi }\urcorner \). Then \((\mathbb {N}, A)\models \lnot \mathrm {Tr} \ulcorner {\lnot \psi }\urcorner \) iff \(\lnot \psi \in A\) iff \(\psi \in E\) iff
. Let \({\textsf {val}} (\ulcorner {t}\urcorner )=\ulcorner {\psi }\urcorner \). Then \((\mathbb {N}, A)\models \lnot \mathrm {Tr} \ulcorner {\lnot \psi }\urcorner \) iff \(\lnot \psi \in A\) iff \(\psi \in E\) iff  iff
iff  .
.
 \(\varphi \equiv \lnot \mathrm {Tr} (t)\) Similar argument: use contraposition and the fact that \((\mathbb {N}, A)\) is a model of \((\mathrm {Tr} \mathrm {Tr})\).
\(\varphi \equiv \lnot \mathrm {Tr} (t)\) Similar argument: use contraposition and the fact that \((\mathbb {N}, A)\) is a model of \((\mathrm {Tr} \mathrm {Tr})\).
The induction step is nearly immediate. We show one example.
 \(\varphi \equiv \lnot \forall v\psi \)
\(\varphi \equiv \lnot \forall v\psi \)  iff for some \(n\in \omega \),
iff for some \(n\in \omega \),  iff, by i.h.,
iff, by i.h.,  . Since \((\mathbb {N}, A)\models (\mathrm {Tr} \lnot \forall )\), this is the case iff
. Since \((\mathbb {N}, A)\models (\mathrm {Tr} \lnot \forall )\), this is the case iff

We now show that
 This amounts to showing that
This amounts to showing that

Suppose  . We have just seen that this is the case iff
. We have just seen that this is the case iff  iff \(\lnot \varphi \in E\) iff \(\lnot \lnot \varphi \in A\). Since \((\mathbb {N}, A)\) is a model of KF, this is the case iff \(\varphi \in A\) iff
iff \(\lnot \varphi \in E\) iff \(\lnot \lnot \varphi \in A\). Since \((\mathbb {N}, A)\) is a model of KF, this is the case iff \(\varphi \in A\) iff  .
.
For the other direction of (ii), we want to show that
If \((E, A)=\Phi (E, A)\), then \((\mathbb {N},A)\models \textsf {KF} \).
Let \((E, A)=\Phi (E, A)\). It suffices to show that the structure \((\mathbb {N}, A)\) classically satisfies the axioms of KF, as rules of inference preserve validity by definition of \(\models \). We show two examples.
 . Let t, s be two closed terms. \((\mathbb {N}, A)\models \mathrm {Tr} \ulcorner {t = s}\urcorner \)Footnote 44
. Let t, s be two closed terms. \((\mathbb {N}, A)\models \mathrm {Tr} \ulcorner {t = s}\urcorner \)Footnote 44
iff \(t=s\in E=\Phi ^E(E, A)\) iff  iff
iff  iff \((\mathbb {N}, A)\models \textsf {val} (\ulcorner {t}\urcorner ) = \textsf {val} (\ulcorner {s}\urcorner )\).
iff \((\mathbb {N}, A)\models \textsf {val} (\ulcorner {t}\urcorner ) = \textsf {val} (\ulcorner {s}\urcorner )\).
 . Let t be a closed term. \((\mathbb {N}, A)\models \mathrm {Tr} \ulcorner {\lnot \mathrm {Tr} (t)}\urcorner \) iff \(\lnot \mathrm {Tr} (t)\notin \Phi ^A(E, A)\). We want to show:
. Let t be a closed term. \((\mathbb {N}, A)\models \mathrm {Tr} \ulcorner {\lnot \mathrm {Tr} (t)}\urcorner \) iff \(\lnot \mathrm {Tr} (t)\notin \Phi ^A(E, A)\). We want to show:

Assume \((\mathbb {N}, A)\models \textsf {Sent} (\textsf {val} (\ulcorner {t}\urcorner ))\) and let \((\mathbb {N}, A)\models \textsf {val} (\ulcorner {t}\urcorner )=\ulcorner {\varphi }\urcorner \). From \(\lnot \mathrm {Tr} (t)=\lnot \mathrm {Tr} \ulcorner {\varphi }\urcorner \notin \Phi ^A(E, A)\) we get  iff \(\varphi \notin E\) iff \(\lnot \varphi \notin A\) iff
iff \(\varphi \notin E\) iff \(\lnot \varphi \notin A\) iff

i.e.,  .
.
For the other direction of the initial sequent \(\mathrm {Tr} \lnot \mathrm {Tr} \), let t again be a closed term. Suppose

If \((\mathbb {N}, A)\models \lnot \textsf {Sent} (\textsf {val} (\ulcorner {t}\urcorner ))\) then  hence \(\lnot \mathrm {Tr} (t)\notin \Phi ^A(E, A)=A\) iff \((\mathbb {N}, A)\models \mathrm {Tr} \ulcorner {\lnot \mathrm {Tr} (t)}\urcorner \), which is what we wanted to show.
hence \(\lnot \mathrm {Tr} (t)\notin \Phi ^A(E, A)=A\) iff \((\mathbb {N}, A)\models \mathrm {Tr} \ulcorner {\lnot \mathrm {Tr} (t)}\urcorner \), which is what we wanted to show.
If  , then let \(\textsf {val} (\ulcorner {t}\urcorner )=\ulcorner {\varphi }\urcorner \). From \((\mathbb {N}, A)\models \mathrm {Tr} \ulcorner {\lnot \varphi }\urcorner \) we get
, then let \(\textsf {val} (\ulcorner {t}\urcorner )=\ulcorner {\varphi }\urcorner \). From \((\mathbb {N}, A)\models \mathrm {Tr} \ulcorner {\lnot \varphi }\urcorner \) we get  iff
iff  iff
iff  iff
iff  hence
hence  iff
iff  , i.e.,
, i.e.,  , which is our desired conclusion.
, which is our desired conclusion.
The proof extends to \(\textsf {KF} _\textsf {S} \) in a straightforward way. In particular, it suffices to show that (i) given a symmetric fixed-point \((E, A)=\Phi (E, A)\), the additional axiom GoG of \(\textsf {KF} _\textsf {S} \) is satisfied in the classical structures \((\mathbb {N}, A)\), and (ii) conversely, given a model \((\mathbb {N}, A)\models \textsf {KF} _\textsf {S} \), the pair \((E, A)=\Phi (E, A)\) is a symmetric fixed-point. For (i), one has to show that, for arbitrary sentences \(\varphi , \psi \)

If the fixed-point is consistent, then the left disjunct is satisfied. If fixed-point is complete, then the right disjunct is satisfied. For (ii), one can use the fact the A is a fixed-point (since \((\mathbb {N}, A)\) is a model of KF, too); the fact that it is either consistent ot complete follows immediately by the fact that it is a model of the axiom GoG, hence it satisfies (1). \(\square \)
Remark 26
It may be worth noticing that there are consistent (complete) fixed-point (E, A) of \(\Phi \), such that the structure \((\mathbb {N}, A)\) does not classically satisfy Cons (Comp), which is why \(\textsf {KF} _\textsf {cs} \) (\(\textsf {KF} _\textsf {cp} \)) is not \(\mathbb {N}\)-categorical\(^+\) relative to the class of consistent (complete) fixed-points.
We finish by proving Proposition 11. As mentioned, the key observation is the following
Lemma 27
For \( {\textsf {KF} _\star ^\circ \in \{\textsf {KF} ^-, \textsf {KF} ^{\textsf {int}} , \textsf {KF} , \textsf {KF} _\textsf {S} ^-, \textsf {KF} ^\mathsf {int} _\textsf {S} , \textsf {KF} _\textsf {S} \}}\) it holds that
This lemma is a corollary of the following
Lemma 28
Let the pair \((\textsf {PKF} _\star , \textsf {KF} _\star )\) range over the following theory-pairs

Then

where \(\mathrm {Tr} \ulcorner {\Gamma }\urcorner :=\{\mathrm {Tr} \ulcorner {\gamma }\urcorner \mid \gamma \in \Gamma \}\).
Proof
See (Castaldo and Stern 2020, Proposition 4.15). \(\square \)
Proof of Lemma 27
\(\textsf {KF} _\star \vdash \varnothing \Rightarrow \mathrm {Tr} \ulcorner {\lnot \varphi }\urcorner \) iff, by Lemma 28, \(\textsf {PKF} _\star \vdash \varnothing \Rightarrow \lnot \varphi \) iff, since contraposition is admissible in \(\textsf {PKF} _\star \), \(\textsf {PKF} _\star \vdash \varphi \Rightarrow \varnothing \) iff \(\textsf {KF} _\star \vdash \mathrm {Tr} \ulcorner {\varphi }\urcorner \Rightarrow \varnothing \) iff by logic \(\textsf {KF} _\star \vdash \varnothing \Rightarrow \lnot \mathrm {Tr} \ulcorner {\varphi }\urcorner \). \(\square \)
Remark 29
\(\textsf {PKF} _\textsf {cs} \) and \(\textsf {PKF} _\textsf {cp} \) do not admit contraposition, and that it why Lemma 27 cannot be extended to these pairs, as without contraposition the argument does not go through.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Castaldo, L. On the Costs of Classical Logic. Erkenn 88, 1157–1188 (2023). https://doi.org/10.1007/s10670-021-00397-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-021-00397-7




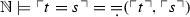 .
.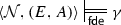 , for all
, for all 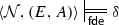 for some
for some 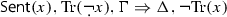 .
.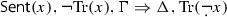 .
.