Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-25T05:47:25.112Z Has data issue: false hasContentIssue false
  • English
  • Français

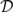${\cal D}$-MAXIMAL SETS

Published online by Cambridge University Press:  22 December 2015

PETER A. CHOLAK ,
PETER GERDES  and
KAREN LANGE
PETER A. CHOLAK
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME NOTRE DAME, IN 46556-5683, USAE-mail: peter.cholak.1@nd.eduURL: http://www.nd.edu/∼cholak
PETER GERDES
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME NOTRE DAME, IN 46556-5683, USAE-mail: gerdes@invariant.org
KAREN LANGE
Affiliation:
DEPARTMENT OF MATHEMATICS WELLESLEY COLLEGE WELLESLEY, MA 02482, USAE-mail: karen.lange@wellesley.eduURL: http://palmer.wellesley.edu/∼klange/
Get access Rights & Permissions [Opens in a new window]

Abstract

Soare [20] proved that the maximal sets form an orbit in ${\cal E}$. We consider here 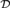${\cal D}$-maximal sets, generalizations of maximal sets introduced by Herrmann and Kummer [12]. Some orbits of 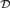${\cal D}$-maximal sets are well understood, e.g., hemimaximal sets [8], but many are not. The goal of this paper is to define new invariants on computably enumerable sets and to use them to give a complete nontrivial classification of the 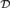${\cal D}$-maximal sets. Although these invariants help us to better understand the 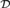${\cal D}$-maximal sets, we use them to show that several classes of 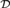${\cal D}$-maximal sets break into infinitely many orbits.

Keywords

computably enumerable sets under inclusionmaximal setsr-maximal setshhsimple sets
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 4 , December 2015 , pp. 1182 - 1210
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Cholak, Peter, Automorphisms of the lattice of recursively enumerable sets. Memoirs of the American Mathematical Society, vol. 113 (1995), no. 541.CrossRefGoogle Scholar
Cholak, Peter and Harrington, Leo A, Isomorphisms of splits of computably enumerable sets, this Journal, vol. 68 (2003), no. 3, pp. 1044–1064.Google Scholar
Cholak, Peter and Harrington, Leo A. Extension theorems, orbits, and automorphisms of the computably enumerable sets. Transactions of the American Mathematical Society, vol. 360 (2008) no. 4, pp. 1759–1791.CrossRefGoogle Scholar
Cholak, Peter and Nies, André, Atomless r-maximal sets. Isreal Journal of Mathematics, vol. 113 (1999), pp. 305–322.CrossRefGoogle Scholar
Cholak, Peter, Downey, Rod, and Herrmann, Eberhard, Some orbits for ${\cal E}$. Annals of Pure and Applied Logic, vol. 107 (2001), no. 1–3, pp. 193–226.CrossRefGoogle Scholar
Cholak, Peter A., Downey, Rodney, and Harrington, Leo A., On the orbits of computably enumerable sets. Journal of the American Mathematical Society, vol. 21 (2008), no. 4, pp. 1105–1135.CrossRefGoogle Scholar
Dëgtev, A. N., Minimal 1-degrees, and truth-table reducibility. Sibirskii Matematicheskii Žhurnal, vol. 17 (1976), no. 5, pp. 1014–1022, 1196.Google Scholar
Downey, R. G. and Stob, Michael, Automorphisms of the lattice of recursively enumerable sets: orbits. Advances in Mathematics, vol. 92 (1992), no. 2, pp. 237–265.CrossRefGoogle Scholar
Harrington, Leo and Soare, Robert I, Post’s program and incomplete recursively enumerable sets. Proceedings of the National Academy of Sciences, U.S.A., vol. 88, no. 22, pp. 10242–10246.CrossRefGoogle Scholar
Herrmann, E., Automorphisms of the lattice of recursively enumerable sets and hyperhypersimple sets. Proceedings of the fourth Easter conference on model theory (Gross Köris, 1986), Seminarberichte, vol. 86, pp. 69–108, Humboldt University, Berlin, 1986.Google Scholar
Herrmann, E., Automorphisms of the lattice of recursively enumerable sets and hyperhypersimple sets. Logic, methodology and philosophy of science, VIII (Moscow, 1987), Studies in Logic and the Foundations of Mathematics, vol. 126, pp. 179–190, North-Holland, Amsterdam, 1989.Google Scholar
Herrmann, Eberhard and Kummer, Martin, Diagonals and ${\cal D}$-maximal sets, this Journal, vol. 59 (1994), no. 1, pp. 60–72. ISSN 0022-4812.Google Scholar
Lachlan, Alistair H., The elementary theory of the lattice of recursively enumerable sets. Duke Mathematical Journal, vol. 35 (1968), pp. 123–146.CrossRefGoogle Scholar
Lachlan, Alistair H., On the lattice of recursively enumerable sets. Transactions of the American Mathematical Society, vol. 130 (1968), pp. 1–37.CrossRefGoogle Scholar
Lerman, M. and Soare, R. I., A decidable fragment of the elementary theory of the lattice of recursively enumerable sets. Transactions of the American Mathematical Society, vol. 257 (1980), no. 1, pp. 1–37.CrossRefGoogle Scholar
Maass, W., On the orbit of hyperhypersimple sets, this Journal, vol. 49 (1984), pp. 51–62.Google Scholar
Maass, W. and Stob, M., The intervals of the lattice of recursively enumerable sets determined by major subsets. Annals of Pure and Applied Logic, vol. 24 (1983), pp. 189–212.CrossRefGoogle Scholar
Martin,  Donald A., Classes of recursively enumerable sets and degrees of unsolvability. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.CrossRefGoogle Scholar
Slaman, Theodore A. and Hugh Woodin, W., Slaman-Woodin conjecture. Personal Communication, 1989.Google Scholar
Soare, Robert I., Automorphisms of the lattice of recursively enumerable sets I: maximal sets. Annals of Mathematics (2), vol. 100 (1974), pp. 80–120.CrossRefGoogle Scholar
Soare, Robert I., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic, Omega Series, Springer-Verlag, Heidelberg, 1987.Google Scholar
Stob, M., The Structure and Elementary Theory of the Recursive Enumerable Sets, PhD thesis, University of Chicago, Illinois 1979.Google Scholar
Weber, Rebecca, Invariance in ${{\cal E}}}$* and ${{\cal E}}}$Π. Transactions of the American Mathematical Society, vol. 358 (2006), no. 7, pp. 3023–3059.CrossRefGoogle Scholar