Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-25T10:53:57.521Z Has data issue: false hasContentIssue false
  • English
  • Français

On finite and infinite modal systems

Published online by Cambridge University Press:  12 March 2014

C. West Churchman
C. West Churchman*
Affiliation:
University of Pennsylvania
Get access Rights & Permissions [Opens in a new window]

Extract

In Oskar Becker's Zur Logik der Modalitäten four systems of modal logic are considered. Two of these are mentioned in Appendix II of Lewis and Langford's Symbolic logic. The first system is based on A1–8 plus the postulate,

From A7: ∼◊p⊰∼p we can prove the converse of C11 by writing ∼◊p for p, and hence derive

The addition of this postulate to A1–8, as Becker points out, allows us to “reduce” all complex modal functions to six, and these six are precisely those which Lewis mentions in his postulates and theorems: p, ∼p, ◊p, ∼◊p, ∼◊∼p, and ◊∼p This reduction is accomplished by showing

where ◊n means that the modal operator ◊ is repeated n times; e.g., ◊3p = ◊◊◊p. Then it is shown that

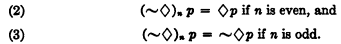
By means of (1), (2), and (3) any complex modal function whatsoever may be reduced to one of the six “simple” modals mentioned above.

It might be asked whether this reduction could be carried out still further, i.e., whether two of the six “irreducible” modals could not be equated. But such a reduction would have to be based on the fact that ◊p = p which is inconsistent with the set B1–9 of Lewis and Langford's Symbolic logic and independent of the set A1–8. Hence for neither set would such a reduction be possible.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 3 , Issue 2 , June 1938 , pp. 77 - 82
Copyright
Copyright © Association for Symbolic Logic 1938

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Jahrbuch für Philosophie und phänomenologische Forschung, vol. 11 (1930), pp. 496–548Google Scholar.

2 The postulate set of Lewis's Survey of symbolic logic.

3 Huntington, E. V., Postulates for assertion, conjunction, negation, and equality, Proceedings of the American Academy of Arts and Sciences, vol. 72 (1937), pp. 1–44Google Scholar.

4 Ibid., Theorem 87.

5 Cf. Smith's, H. B. (identical) “induction formula,” Abstract logic or the science of modality, Philosophy of science, vol. 1 (1934), pp. 369–397Google Scholar. This formula was discovered independently.

6 P. C. Rosenbloom has been able to dispense with the concept of number altogether in this postulate (Postulate set for Smith's theory of modal logic, as yet unpublished).

7 Becker actually generalizes this Rule to the extent of saying that Mp⊰Mq can be asserted, where M is any “affirmative” modal, that is, any modal with an even number of negation signs or “curls.” But for our purpose, the form here given is sufficient. As a matter of fact, by means of this form and the set A1–8, the general form can be proved. It is also worth noting that the implication p⊰g in the Rule refers to an implication between modal functions; i.e., p and q are modal functions of the same variable; p might be ∼◊∼T and q be ◊r. Put otherwise, p⊰q is thought of as being any theorem which follows from A7 or the generalized Brouwerian Axiom.

8 This assertion needs, of course, the qualification that other “traditional” laws be observed; in particular, those assumptions which we set down below.

9 Mind, n.s. vol. 43 (1934), pp. 78–80.

10 Actually, we prove something stronger than Becker's Rule, but for our purposes, the assumption that p⊰q is a theorem or postulate is enough.

11 Bulletin of the American Mathematical Society, vol. 42 (1936), pp. 743–746CrossRefGoogle Scholar.

12 This is theorem 19.13 in Lewis and Langford's Symbolic logic.

13 C11 hardly enables us to determine the truth or falsity of any “meaningful expression” of the system, however. For instance, the truth of (p⊰q)⊰(◊p⊰q) or ◊(pq) = Pq is still undetermined.

14 These numbers refer to the theorems as they appear in Lewis and Langford's Symbolic logic.

15 When the converse of this axiom is postulated, ∼◊∼◊∼p⊰q then the system is not necessarily finite; cf. the system based on C14 above, which is apparently infinite, though it includes A8 and hence Becker's Rule. But the converse of the Brouwerian Axiom is somewhat paradoxical, at least when verbally interpreted. If p=∼◊∼◊p is the axiom, an infinite system is possible also.

16 Let q=0 (“0” is any statement satisfying the proposition p⊰p, i.e., any impossible statement). Then the law becomes (p⊰.⊰T)⊰(p⊰T). The premiss 0⊰T is true in Smith's system and may be suppressed. Hence the law reduces to (p⊰)⊰(p⊰). We may express the premiss as ∼◊p and the conclusion as ∼◊(p∼ r) by the definition of implication; so that ∼◊p ⊰ ∼◊(p∼r. By contradiction and transposition we get B8: ◊(P ∼r) ⊰ ◊P.