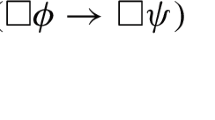Abstract
Criteria of acceptability for mathematical proofs are field-dependent. In topology, though not in most other domains, it is sometimes acceptable to appeal to visual intuition to support inferential steps. In previous work (De Toffoli and Giardino in Erkenntnis 79(3):829–842, 2014; Lolli, Panza, Venturi (eds) From logic to practice, Springer, Berlin, 2015; Larvor (ed) Mathematical cultures, Springer, Berlin, 2016) my co-author and I aimed at spelling out how topological proofs work on their own terms, without appealing to formal proofs which might be associated with them. In this article, I address two criticisms that have been raised in Tatton-Brown (Erkenntnis, 2019. https://doi.org/10.1007/s10670-019-00180-92019) against our approach: (1) that it leads to a form of relativism according to which validity is equated with social agreement and (2) that it implies an antiformalizability thesis according to which it is not the case that all rigorous mathematical proofs can be formalized. I reject both criticisms and suggest that our previous case studies provide insight into the plausibility of two related but quite different theses.



Similar content being viewed by others
Notes
As it is customary, I use the term ‘proof’ as a success term. If not specified otherwise, I will use the term ‘proof’ to mean ‘informal proof.’
I am here focusing on classical logic and leaving aside issues raised by rejection of the law of excluded middle or of other non-classical logical choices.
The issue is however by no means settled. For example, the acceptance of large cardinal axioms is still a matter of debate. Moreover, nowadays category theory and homotopy type theory offer alternative foundations.
From now referred to as (TB19).
From now referred to as (DG16).
Note that not all mathematicians are reasonable. Some did actually try the impossible and proposed arguments doomed to be refuted. (TB19, p. 8) also mentions independence results. Thanks to John Burgess for conversations about this issue.
See Ferreirós (2016, Ch. 2) for a discussion of mathematical communities.
Translated by Cornford.
See Hamami (2019) for a meticulous analysis of mathematical rigor and the historical underpinning of the present account.
De Toffoli and Giardino (2014, 2015, 2016) are here labelled (DG14), (DG15), and (DG16). After publishing a paper on knot diagrams in Erkenntnis in 2014, Giardino and I wrote an initial draft on the topic of low-dimensional topology for two conferences which later was developed and split into two papers, then published in 2015 and 2016 as chapters in the two conference proceedings.
Although they could be—as in formal diagrammatic proofs.
In a similar vein, Jeremy Avigad (2020) proposes an account of how traditional proofs are reliable, tracking existence of formal proofs.
As one referee pointed out, part of the disagreement with Tatton-Brown derives from the fact that we talked past each other.
Von Neumann’s density theorem is the example that Jones (1998) uses to contrast Alexander’s theorem.
I am putting aside the (interesting) phenomenon of computer-assisted proofs or proofs requiring collaborations to focus on the phenomenon of proof that can be grasped by a single mathematician.
Don Fallis (2003) proposes a taxonomy and analysis of different gaps in mathematical proofs.
This is in line with Tatton-Brown. However, he takes the criteria of acceptability to be the criteria of rigor; this is where our projects take different directions.
Still, not by sheer chance infinitesimal worked pretty well in practice and in the right hands and this has been partially revindicated by Robinson’s non-standard analysis.
See Parikh (2009).
Thanks to Kevin Buzzard for discussions on the shortcomings of contemporary standard of acceptability for rigorous proofs and to Patrick Massot for pointing me to this specific controversy.
These are papers by Fukaya and co-authors published in main mathematical journals: K. Fukaya and K. Ono, Arnold conjecture and Gromov–Witten invariants, Topology 38 (1999), 933–1048, and K. Fukaya, Y.-G. Oh, H. Ohta, and K. Ono, Lagrangian Intersection Theory, Anomaly and Obstruction, Parts I and II, AMS/IP Studies in Advanced Mathematics, Amer. Math. Soc. and Internat. Press.
See Avigad and Harrison (2014). Computer assisted proofs are among the first proof candidates for formal verification. Great achievements have already been obtained; among the most pathbreaking are the formalizations of the Four-Color Theorem by Georges Gonthier in 2004 and of the proof of the Kepler Conjecture by Tom Hales and his collaborators of the Flyspek project in 2017.
After ten years and various vicissitudes, he found a mistake in his previous work.
I use the term ‘intuition’ in sense of the German word ‘Anschauung.’ There are other types of intuition that play a role in mathematics. For example, mathematical intuition á la Gödel is what leads us to the justification of the axioms of set theory. Thanks to one of the anonymous referees for this point.
“A grand insight delivered with beautiful but insufficient hints, the proof was never fully published” (Jaffe and Quinn 1993, p. 7).
“Poincaré claimed too much, proved too little, and his “reckless” methods could not be imitated. […] Dieudonné suggests that casual reasoning is a childhood disease of mathematical areas and says, “…after 1910… uniform standards of what constitutes a correct proof became universally accepted in topology… this standard has remained unchanged ever since.” But in fact, there have been many further episodes.” (Jaffe and Quinn 1993, p. 8).
For example, Hales estimated that the process of formalizing his proof of the Kepler Conjecture in HOL Light took 20 working years (distributed across many people) to complete.
This is in line with Burgess’ (2015) claim that mathematicians are indifferent to foundational choices.
As explained in footnote 11, there is continuity between (DG15) and (DG16).
For instance, in the second quarter of the 20th century, Artin, the father of braid theory, shows changes of mind with respect to his own methodology, particularly with the use of diagrams. See Friedman (2019) for a detailed historical account of the issue.
See Kennedy (2009) for a review emphasizing this point.
Of course, if any formal system is allowed, then this thesis is utterly trivial since we can always add more axioms.
For reasons of space, I cannot go into the mathematical details, but I limit myself to addressing some specific critiques.
See for example (DG16, p. 27). The strong criticism of a logic-based approach to mathematics was in line with early work in the philosophy of mathematical practice, and in particular with Lakatos’ (1963, p. X) discussion of the dangers of a formalist philosophy. This was a starting point in Giardino’s doctoral research.
See (DG16) and (TB19) for the details.
Alexander does not use such terminology, which is adopted in Dalvit (2011).
Elsewhere, Alexander writes: “In the figures, we shall picture a knot by a smooth curve rather than by a polygon. A purist may think of the curve as a polygon consisting of so many tiny sides that it gives an impression of smoothness.” (Alexander 1928, 276). Admittedly, we could have taken this approach as well.
Jones’ illustration reported in (DG16, p. 42) is bad since it depicts the very simple case in which no extra crossings are created by performing the move (and seems to suggest that all cases are that simple–but they are not).
If one counts the setting up of preliminary results, she takes six pages (pp. 39–44), but she proves a slightly more general result.
Thanks to Michael Barany for conversation on the policies of the PNAS at the time of Alexander’s publication.
Even if Alexander’s paper does not include diagrams of knots, the author asks the reader to imagine them.
The Reidemeister theorem establishes that all transformations on knot diagrams that leave invariant the represented knot type can be decomposed into a sequence of three simple local diagrammatic moves. In three dimensions, the second Reidemeister move consists in bringing a strand under or above another strand. Diagrammatically this leads to the introduction of two new crossings, as in Fig. 3.
Thanks to John Sullivan for this point.
This goes against Tatton-Brown’s (2019, p. 11) claim that in our framework the permissible actions form a “fixed list.”
See (DG14) for the case of knot diagrams and (De Toffoli 2019, Ch. 2–3) for general discussion of how only a subset of all perceptual features of a figure can be relevant for the corresponding diagram.
Birman is very clear in her own version of the proof and bypasses the problem completely, since her operation is done in parallel rather than sequentially.
In (DG16) we used what Thurston calls “shared mental model[s]” (1994, p. 174) to characterize the context formed by a particular sub-field. However, this expression is infelicitous because mental models are generally considered as subjective representations (and therefore not “shared”).
This is clearer in (DG15).
Jeremy Avigad (2020) addresses exactly the question of where the reliability of mathematicians comes from. In his terminology, he wants to understand how the robustness of informal mathematical proofs (which is a condition for us to get knowledge from them) can be squared with the fragility of formal proofs, in which a single tiny error invalidates the whole argument.
See also (De Toffoli 2017).
See (De Toffoli 2019, Ch. 1).
Clearly, this is the same generality problem that arises in the case of Euclidean diagrams.
Thanks to one of the referees for suggesting that I discuss this point.
I plan to say more about this in future work.
This is suggested in (TB19). However, in practice, the possibility of resolving disagreement in this way is often impracticable. This is exemplified by the persistent disagreement with respect to the abc Conjecture. The Japanese mathematician Shinichi Mochizuki put forward a putative proof in 2012 that has been challenged by the Fields medalist Peter Scholze and remains controversial to this day.
References
Alexander, J. (1923). A lemma on systems of knotted curves. Proceedings of the National Academy of Sciences of the United States of America, 9(3), 93.
Alexander, J. (1928). Topological invariants of knots and links. Transactions of the American Mathematical Society, 30(2), 275–306.
Ashton, Z. (2020). Audience role in mathematical proof development. Synthese. Audience role in mathematical proof development.
Avigad, J. (2020). Reliability of mathematical inference. Synthese. https://doi.org/10.1007/s11229-019-02524-y.
Avigad, J., & Harrison, J. (2014). Formally verified mathematics. Communications of the ACM, 57(4), 66–75.
Azzouni, J. (2004). The derivation-indicator view of mathematical practice. Philosophia Mathematica, 12(3), 81–105.
Birman, J. (1974). Braids, links, and mapping class groups (AM-82). Princeton: Princeton University Press.
Dalvit, E. (2011). New proposals for the popularization of braid theory. Trento: Università degli Studi di Trento.
De Toffoli, S. (2017). `Chasing’ the diagram: The use of visualizations in algebraic reasoning. The Review of Symbolic Logic, 10(1), 158–186.
De Toffoli, S. (2019). Epistemic roles of mathematical diagrams. Stanford: Stanford University.
De Toffoli, S., & Giardino, V. (2014). Roles and forms of diagrams in knot theory. Erkenntnis, 79(3), 829–842.
De Toffoli, S., & Giardino, V. (2015). An inquiry into the practice of proving in low-dimensional topology. In G. Lolli, M. Panza, & G. Venturi (Eds.), From logic to practice (pp. 315–336). Berlin: Springer.
De Toffoli, S., & Giardino, V. (2016). Envisioning transformations—the practice of topology. In B. Larvor (Ed.), Mathematical cultures (pp. 25–50). Berlin: Springer.
Epple, M. (2004). Knot invariants in Vienna and Princeton during the 1920s: Epistemic configurations of mathematical research. Science in Context, 17(1/2), 131–164.
Fallis, D. (2003). Intentional gaps in mathematical proofs. Synthese, 134, 45–69.
Ferreirós, J. (2016). Mathematical knowledge and the interplay of practices. Princeton: Princeton University Press.
Friedman, M. (2019). Mathematical formalization and diagrammatic reasoning: The case study of the braid group between 1925 and 1950. British Journal for the History of Mathematics, 34(1), 43–59. https://doi.org/10.1080/17498430.2018.1533298.
Giaquinto, M. (2008). Visualizing in mathematics. In P. Mancosu (Ed.), The philosophy of mathematical practice (pp. 22–42). Oxford: Oxford University Press.
Gowers, T. (Ed.). (2008). The Princeton companion to mathematics (3rd ed.). Princeton: Princeton University Press.
Hahn, H. (1980). The crisis in intuition. In Empiricism, Logic and Mathematics (pp. 73–102). Springer, Berlin.
Hales, T. C. (2008). Formal proofs. Notices of the American Mathematical Society, 55(11), 1370–1380.
Hamami, Y. (2019). Mathematical rigor and proof. The Review of Symbolic Logic, 1, 1. https://doi.org/10.1017/S1755020319000443.
Hartnett, K. (2017). A Fight to Fix Geometry’s Foundations. Quanta Magazine.
Hersh, R. (2014). Experiencing mathematics: What do we do, When we do mathematics?. Providence: American Mathematical Society.
Jaffe, A., & Quinn, F. (1993). Theoretical mathematics: Toward a cultural synthesis of mathematics and theoretical physics. Bulletin of the American Mathematical Society, 29(1), 1–13.
Jones, V. F. R. (1998). A credo of sorts. In H. G. Dales & G. Oliveri (Eds.), Truth in mathematics (pp. 203–214). Oxford: Oxford University Press.
Kennedy, J. (2009). Review: Princeton companion to mathematics. Bulletin of Symbolic Logic, 15(4), 431–436.
Lakatos, I. (1963). Proofs and refutations. Cambridge: Cambridge University Press.
Leitgeb, H. (2009). On formal and informal provability. In Ø. Linnebo & O. Bueno (Eds.), New waves in philosophy of mathematics (pp. 263–299). London: Palgrave Macmillan.
McDuff, D., & Wehrheim, K. (2015). Kuranishi atlases with trivial isotropy: The 2013 state of affairs. arXiv:1208.1340 [math].
Parikh, C. (2009). The Unreal Life of Oscar Zariski. Berlin: Springer.
Rav, Y. (1999). Why do we prove theorems? Philosophia Mathematica, 7(3), 5–41.
Steiner, M. (1975). Mathematical knowledge. Ithaca: Cornell University Press.
Tanswell, F. (2015). A problem with the dependence of informal proofs on formal proofs. Philosophia Mathematica, 23(3), 295–310.
Tatton-Brown, O. (2019). Rigor and intuition. Erkenntnis. https://doi.org/10.1007/s10670-019-00180-9.
Acknowledgements
Special thanks to Juliette Kennedy for her extensive and valuable feedback. Thanks are also due to Jeremy Avigad, John Burgess, Andrew Chignell, Tom Ryckman, and John Sullivan their suggestions. I wish to thank my previous co-author, Valeria Giardino for long conversations on the topic. Lastly, I wish to thank the two anonymous referees for their valuable comments, which helped me to greatly improve this paper.
Funding
The funding was provided by Princeton University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
De Toffoli, S. Reconciling Rigor and Intuition. Erkenn 86, 1783–1802 (2021). https://doi.org/10.1007/s10670-020-00280-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-020-00280-x