Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-23T13:41:09.841Z Has data issue: false hasContentIssue false
  • English
  • Français

A HIERARCHY OF COMPUTABLY ENUMERABLE DEGREES

Published online by Cambridge University Press:  26 April 2018

ROD DOWNEY  and
NOAM GREENBERG
ROD DOWNEY
Affiliation:
SCHOOL OF MATHEMATICS AND STATISTICS VICTORIA UNIVERSITY P.O. BOX 600 WELLINGTON, NEW ZEALANDE-mail:Rod.Downey@vuw.ac.nz
NOAM GREENBERG
Affiliation:
SCHOOL OF MATHEMATICS AND STATISTICS VICTORIA UNIVERSITY P.O. BOX 600 WELLINGTON, NEW ZEALANDE-mail:greenberg@msor.vuw.ac.nz
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a new hierarchy of computably enumerable degrees. This hierarchy is based on computable ordinal notations measuring complexity of approximation of 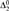${\rm{\Delta }}_2^0$ functions. The hierarchy unifies and classifies the combinatorics of a number of diverse constructions in computability theory. It does so along the lines of the high degrees (Martin) and the array noncomputable degrees (Downey, Jockusch, and Stob). The hierarchy also gives a number of natural definability results in the c.e. degrees, including a definable antichain.

Keywords

03D25computably enumerabletotally α-computably approximablemultiple permittinglattice embedding
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 24 , Issue 1 , March 2018 , pp. 53 - 89
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Afshari, B., Barmpalias, G., Cooper, S. B., and Stephan, F., Post’s programme for the Ershov hierarchy. Journal of Logic and Computation, vol. 17 (2007), no. 6, pp. 1025–1040.Google Scholar
Ambos-Spies, K., Downey, R. G., and Monath, M., On the Sacks splitting theorem and approximating computations, in preparation.Google Scholar
Ambos-Spies, K., Fang, N., Losert, N., Merkle, W., and Monath, M., Array noncomputability: A modular approach, in preparation.Google Scholar
Ambos-Spies, K. and Fejer, P. A., Embeddings of N5 and the contiguous degrees.Annals of Pure and Applied Logic, vol. 112 (2001), no. 2–3, pp. 151–188.CrossRefGoogle Scholar
Ambos-Spies, K., Jockusch, C. G. Jr., Shore, R A., and Soare, R. I., An algebraic decomposition of the recursively enumerable degrees and the coincidence of several degree classes with the promptly simple degrees.Transactions of the American Mathematical Society, vol. 281 (1984), no. 1, pp. 109–128.CrossRefGoogle Scholar
Ambos-Spies, K. and Losert, N., Universally array noncomputable sets, in preparation.Google Scholar
Ambos-Spies, K., Losert, N., and Monath, M., Array noncomputable left-c.e. reals, in preparation.Google Scholar
Anderson, B. and Csima, B., A bounded jump for the bounded Turing degrees.Notre Dame Journal of Formal Logic, vol. 55 (2014), no. 2, pp. 245–264.Google Scholar
Arthur, K., Maximality in the α-c.a. degrees, Master’s thesis, Victoria University of Wellington, 2016.Google Scholar
Arthur, K., Downey, R. G., Greenberg, N., and Turetsky, D., The distribution of maximality in the totally α-c.a. degrees, submitted.Google Scholar
Barmpalias, G., Hypersimplicity and semicomputability in the weak truth table degrees. Archive for Mathematical Logic, vol. 44 (2005), no. 8, pp. 1045–1065.Google Scholar
Barmpalias, G. and Downey, R. G., Kobayashi compressibility. Theoretical Computer Science, vol. 675 (2017), pp. 89–100.Google Scholar
Barmpalias, G., Downey, R. G., and Greenberg, N., Working with strong reducibilities above totally ω-c.e. and array computable degrees. Transactions of the American Mathematical Society, vol. 362 (2010), no. 2, pp. 777–813.Google Scholar
Barmpalias, G., Downey, R. G., and McInerney, M., Integer valued betting strategies and Turing degrees. Journal of Computer and System Sciences, vol. 81 (2015), no. 7, pp. 1387–1412.CrossRefGoogle Scholar
Barmpalias, G., Lewis, A. E. M., and Ng, K. M., The importance of ${\rm{\Pi }}_1^0$ classes in effective randomness. Journal of Symbolic Logic, vol. 75 (2010), no. 1, pp. 387–400.Google Scholar
Bickford, M. and Mills, C. F., Lowness properties of r.e. sets, manuscript, UW Madison, 1982.Google Scholar
Brodhead, P., Downey, R., and Ng, K. M., Bounded randomness, Computation, Physics and Beyond (Dinneen, M. J., Khoussainov, B., and Nies, A., editors), Lecture Notes in Computer Science, vol. 7160, Springer, Heidelberg, 2012, pp. 59–70.Google Scholar
Chisholm, J., Chubb, J., Harizanov, V. S., Hirschfeldt, D. R., Jockusch, C. G. Jr., McNicholl, T., and Pingrey, S., ${\rm{\Pi }}_1^0$ classes and strong degree spectra of relations. Journal of Symbolic Logic, vol. 72 (2007), no. 3, pp. 1003–1018.Google Scholar
Cholak, P., Coles, R., Downey, R. G., and Herrmann, E., Automorphisms of the lattice of ${\rm{\Pi }}_1^0$ classes: Perfect thin classes and anc degrees. Transactions of the American Mathematical Society, vol. 353 (2001), no. 12, pp. 4899–4924.Google Scholar
Cholak, P., Downey, R. G., and Walk, S., Maximal contiguous degrees. Journal of Symbolic Logic, vol. 67 (2002), no. 1, pp. 409–437.CrossRefGoogle Scholar
Cholak, P. A. and Harrington, L. A., On the definability of the double jump in the computably enumerable sets. Journal of Mathematical Logic, vol. 2 (2002), no. 2, pp. 261–296.Google Scholar
Coles, R. J., Downey, R. G., and Laforte, G. L., Notes on wtt-jump and ordinal notations. Manuscript, 1998.Google Scholar
Cooper, S. B., Minimal pairs and high recursively enumerable degrees. Journal of Symbolic Logic, vol. 39 (1974), pp. 655–660.Google Scholar
Day, A. R., Indifferent sets for genericity. Journal of Symbolic Logic, vol. 78 (2013), no. 1, pp. 113–138.CrossRefGoogle Scholar
Diamondstone, D., Greenberg, N., and Turetsky, D., Natural large degree spectra. Computability, vol. 2 (2013), no. 1, pp. 1–8.Google Scholar
Downey, R. G., Lattice nonembeddings and initial segments of the recursively enumerable degrees. Annals of Pure and Applied Logic, vol. 49 (1990), no. 2, pp. 97–119.Google Scholar
Downey, R. G. and Greenberg, N., A transfinite hierarchy of lowness notions in the computably enumerable degrees, unifying classes, and natural definability, submitted.Google Scholar
Downey, R. G. and Greenberg, N., Totally < ωω computably enumerable and m-topped degrees, Theory and Applications of Models of Computation (Cai, J.-Y., Cooper, S. B., and Li, A., editors), Lecture Notes in Computer Science, vol. 3959, Springer, Berlin, 2006, pp. 46–60.Google Scholar
Downey, R. G. and Greenberg, N., Turing degrees of reals of positive effective packing dimension. Information Processing Letters, vol. 108 (2008), no. 5, pp. 298–303.Google Scholar
Downey, R. G., Greenberg, N., and Weber, R., Totally ω-computably enumerable degrees and bounding critical triples. Journal of Mathematical Logic, vol. 7 (2007), no. 2, pp. 145–171.Google Scholar
Downey, R. G. and Hirschfeldt, D. R., Algorithmic Randomness and Complexity, Theory and Applications of Computability, Springer, New York, 2010.Google Scholar
Downey, R. G., Hirschfeldt, D. R., Nies, A., and Stephan, F., Trivial reals, Proceedings of the 7th and 8th Asian Logic Conferences (Downey, R., Cing, D., Tung, S. P., Qui, Y. H., Yasugi, M., and Wu, G., editors), Singapore University Press, Singapore, 2003, pp. 103–131.Google Scholar
Downey, R. G. and Jockusch, C. G. Jr., T-degrees, jump classes, and strong reducibilities. Transactions of the American Mathematical Society, vol. 301 (1987), no. 1, pp. 103–136.Google Scholar
Downey, R. G., Jockusch, C. G. Jr., and Stob, M., Array nonrecursive sets and multiple permitting arguments, Recursion Theory Week (Oberwolfach, 1989) (Amboes-Spies, K., Müller, G. H., and Sacks, G. E., editors), Lecture Notes in Mathematics, vol. 1432, Springer, Berlin, 1990, pp. 141–173.Google Scholar
Downey, R. G., Jockusch, C. G. Jr., and Stob, M., Array nonrecursive degrees and genericity, Computability, Enumerability, Unsolvability (Cooper, S. B., Slaman, T. A., and Wainer, S. S., editors), London Mathematical Society Lecture Note Series, vol. 224, Cambridge University Press, Cambridge, 1996, pp. 93–104.Google Scholar
Downey, R. G. and Lempp, S., Contiguity and distributivity in the enumerable Turing degrees. Journal of Symbolic Logic, vol. 62 (1997), no. 4, pp. 1215–1240.Google Scholar
Downey, R. G. and Ng, K. M., Splitting into degrees with low computational complexity, submitted.Google Scholar
Downey, R. G. and Shore, R. A., Degree-theoretic definitions of the low2 recursively enumerable sets. Journal of Symbolic Logic, vol. 60 (1995), no. 3, pp. 727–756.Google Scholar
Downey, R. G. and Shore, R. A., Lattice embeddings below a nonlow2 recursively enumerable degree. Israel Journal of Mathematics, vol. 94 (1996), pp. 221–246.Google Scholar
Downey, R. G. and Stephenson, J., Avioding effective packing dimension 1 below array noncomputable c.e. degrees, submitted.Google Scholar
Downey, R. G. and Stob, M., Structural interactions of the recursively enumerable T- and w-degrees. Annals of Pure and Applied Logic, vol. 31 (1986), no. 2–3, pp. 205–236. Special issue: Second Southeast Asian logic conference (Bangkok, 1984).Google Scholar
Ershov, Y. L., A certain hierarchy of sets. I. Algebra i Logika, vol. 7 (1968), no. 1, pp. 47–74.Google Scholar
Ershov, Y. L., A certain hierarchy of sets. II. Algebra i Logika, vol. 7 (1968), no. 4, pp. 15–47.Google Scholar
Ershov, Y. L., A certain hierarchy of sets. III. Algebra i Logika, vol. 9 (1970), pp. 34–51.Google Scholar
Figueira, S., Miller, J. S., and Nies, A., Indifferent sets. Journal of Logic and Computation, vol. 19 (2009), no. 2, pp. 425–443.Google Scholar
Franklin, J. N. Y., Greenberg, N., Stephan, F., and Wu, G., Anti-complex sets and reducibilities with tiny use. Journal of Symbolic Logic, vol. 78 (2013), no. 4, pp. 1307–1327.CrossRefGoogle Scholar
Greenberg, N., The role of true finiteness in the admissible recursively enumerable degrees. Memoirs of the American Mathematical Society, vol. 181 (2006), no. 854, vi + 99 pp.Google Scholar
Harrington, L. and Soare, R. I., Post’s program and incomplete recursively enumerable sets. Proceedings of the National Academy of Sciences of the United States of America, vol. 88 (1991), no. 22, pp. 10242–10246.Google Scholar
Ishmukhametov, S., Weak recursive degrees and a problem of Spector, Recursion Theory and Complexity (Kazan, 1997) (Arslanov, M. M. and Lempp, S., editors), De Gruyter Series in Logic and its Applications, vol. 2, de Gruyter, Berlin, 1999, pp. 81–87.Google Scholar
Jockusch, C. G. Jr. and Posner, D. B., Double jumps of minimal degrees. Journal of Symbolic Logic, vol. 43 (1978), no. 4, pp. 715–724.Google Scholar
Kjos-Hanssen, B., Merkle, W., and Stephan, F., Kolmogorov complexity and the recursion theorem. Transactions of the American Mathematical Society, vol. 363 (2011), no. 10, pp. 5465–5480.Google Scholar
Kummer, M., Kolmogorov complexity and instance complexity of recursively enumerable sets. SIAM Journal on Computing, vol. 25 (1996), no. 6, pp. 1123–1143.Google Scholar
Kurtz, S. A., Randomness and genericity in the degrees of unsolvability, Ph.D. dissertation, University of Illinois, Urbana, 1981.Google Scholar
Lachlan, A. H., Embedding nondistributive lattices in the recursively enumerable degrees, Conference in Mathematical Logic—London ’70 (Hodges, W., editor), Lecture Notes in Mathematics, vol. 255, Springer, Berlin, 1972, pp. 149–177.Google Scholar
Lachlan, A. H., Bounding minimal pairs. Journal of Symbolic Logic, vol. 44 (1979), no. 4, pp. 626–642.Google Scholar
Lachlan, A. H. and Soare, R. I., Not every finite lattice is embeddable in the recursively enumerable degrees. Advances in Mathematics, vol. 37 (1980), no. 1, pp. 74–82.CrossRefGoogle Scholar
Lempp, S. and Lerman, M., A finite lattice without critical triple that cannot be embedded into the enumerable Turing degrees. Annals of Pure and Applied Logic, vol. 87 (1997), no. 2, pp. 167–185. Logic Colloquium ’95 Haifa.Google Scholar
Lempp, S., Lerman, M., and Solomon, D. R., Embedding finite lattices into the computably enumerable degrees—a status survey, Logic Colloquium ’02 (Chatzidakis, Z., Koepke, P., and Pohlers, W., editors), Lecture Notes in Logic, vol. 27, The Association for Symbolic Logic, La Jolla, CA, 2006, pp. 206–229.Google Scholar
Lerman, M., The embedding problem for the recursively enumerable degrees, Recursion Theory (Ithaca, NY, 1982) (Nerode, A. and Shore, R. A., editors), Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, Providence, RI, 1985, pp. 13–20.Google Scholar
Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.Google Scholar
McInerney, M., Topics in algorithmic randomness and computability theory, Ph.D. thesis, Victoria University of Wellington, 2016.Google Scholar
Moschovakis, Y. N., Many-one degrees of the predicates H a(x).Pacific Journal of Mathematics, vol. 18 (1966), pp. 329–342.Google Scholar
Nies, A., Lowness properties and randomness. Advances in Mathematics, vol. 197 (2005), no. 1, pp. 274–305.Google Scholar
Nies, A., Computability and Randomness, Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.Google Scholar
Nies, A., Shore, R. A., and Slaman, T. A., Interpretability and definability in the recursively enumerable degrees. Proceedings of the London Mathematical Society (3), vol. 77 (1998), no. 2, pp. 241–291.Google Scholar
Post, E. L., Recursively enumerable sets of positive integers and their decision problems.Bulletin of the American Mathematical Society, vol. 50 (1944), pp. 284–316.Google Scholar
Shore, R. A., The recursively enumerable α-degrees are dense. Annals of Mathematical Logic, vol. 9 (1976), no. 1–2, pp. 123–155.Google Scholar
Shore, R. A., Natural definability in degree structures, Computability Theory and its Applications (Boulder, CO, 1999) (Cholak, P. A., Lempp, S., Lerman, M., and Shore, R. A., editors), Contemporary Mathematics, vol. 257, American Mathematical Society, Providence, RI, 2000, pp. 255–271.Google Scholar
Slaman, T. A., The density of infima in the recursively enumerable degrees. Annals of Pure and Applied Logic, vol. 52 (1991), no. 1–2, pp. 155–179. International Symposium on Mathematical Logic and its Applications (Nagoya, 1988).Google Scholar
Soare, R. I., Recursive theory and Dedekind cuts. Transactions of the American Mathematical Society, vol. 140 (1969), pp. 271–294.Google Scholar
Spector, C., Recursive well-orderings. Journal of Symbolic Logic, vol. 20 (1955), pp. 151–163.Google Scholar
Stephan, F. and Wu, G., Presentations of k-trivial reals and kolmogorov complexity, New Computational Paradigms (First Conference on Computability in Europe, CiE 2005, Amsterdam, The Netherlands, June 8-12, 2005. Proceedings) (Cooper, S. B., Löwe, B., and Torenvliet, L., editor), Lecture Notes in Computer Science, vol. 3526, Springer, 2005, pp. 461–469.Google Scholar
Walk, S. M., Towards a definition of the array computable degrees. Ph.D. thesis, University of Notre Dame, 1999.Google Scholar
Wang, Y., Randomness and complexity. Ph.D. thesis, University of Heidelberg, 1996.Google Scholar
Weinstein, B., Embedding of the lattice 1-3-1 into the recursively enumerable degrees, Ph.D. thesis, University of California, Berkeley, 1988.Google Scholar