Abstract
Two dichotomies are considered as the foundations of a scientific theory: the kind of infinity—either potential or actual-, and the kind of organization of the theory—axiomatic or problem-based. The original intuitionist program relied on the choices of potential infinity and the problem-based organization. I show that the logical theory of Kolmogorov’s 1932 paper relied on the same choices. A comparison of all other theories sharing the same foundational choices allows us to characterize their common theoretical development through a few logical steps. The theory illustrated by Kolmogorov’s paper is then rationally re-constructed according to the steps of this kind of development. One obtains a new foundation of intuitionist logic, which is of a structural kind since it is based on and developed according to the structure of the above mentioned two fundamental choices. In addition, Kolmogorov’s illustration of his theory of intuitionist logic is an instance of rigorous reasoning of the intuitionist kind.
Similar content being viewed by others
Notes
Notice that each modal word is equivalent to a DNP; e.g. “it is
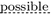 that…” is equivalent to “It is not true that it is not…”. This equivalence is confirmed by the S4 translation of model logic into IL These words will be pointwise underlined, while the two negative words of a DNP will be underlined continuously.
that…” is equivalent to “It is not true that it is not…”. This equivalence is confirmed by the S4 translation of model logic into IL These words will be pointwise underlined, while the two negative words of a DNP will be underlined continuously.An application of PSR changing the final predicate of a PO theory constitutes a move by an author that is of a subjective and intuitive nature, because no logical argument of a specific kind of logic can justify it. In my opinion it represents Beth’s “unavoidable appeal of a form of intuitive knowledge of Mathematics” ([1], p. 645). Moreover, it is the ultimate justification of Brouwer’s appeal to a subjective viewpoint of mathematics and logic. It represents in a PO theory that intuitive element which according to Goedel’s theorems cannot be captured by an AO theory.
Their debate on the foundations of mathematics is illustrated in the light of the two dichotomies in [7].
Here and in the following quotations the word “intuitionistic” will be replaced by the word “intuitionist”.
These papers have been already studied by [5].
In this Sect. the reference to a page of Kolmogorov’s 1932 paper will be indicated by means of a number in round brackets.
I will refer to the text in [17]. For a further translation from German, see J. Mckinna’s site: inf.ed.ac.uk/McKinna. (I thank Miriam Franchella for suggesting it to me).
Since 1987 texts of OP theories have been analyzed by means of DNPs: classical chemistry, S. Carnot’s thermodynamics, L. Carnot’s mechanics, Lagrange’s mechanics, Lobachevsky’s theory of parallels, Galois’ theory, etc. For the methodology and the results see [6].
In order to simplify the following analysis, I will omit a proposition including only a modal word, such as “can”, “must”, “should”, “necessary”, etc. Rigorously, it is equivalent to a doubly negated proposition, but the recognition of a true DNP is more difficult and moreover it may be considered, as in fact it is in some cases, a mere colloquial way of speaking. The following belong to this category: “without misunderstandings” (p. 329), “no difficulties” (p. 330), and “cannot lead to any misunderstandings” (fn. no. 6).
References
Beth, E.W.: The Foundations of Mathematics. A Study in the Philosophy of Science. North-Holland, Amsterdam (1959), chp.s X, XII, XIV (in a reduced version: Foundations of Mathematics, Harper, New York, 1959, ch. I, 2)
Bishop, E.: Constructive Analysis. Mc Graw-Hill, New York (1967)
Brouwer, L.E.W.: Unreliability of the logical principles. In: Brouwer, L.E.J. (ed.) [1975] Collected Works, pp. 107–111. North-Holland, Amsterdam (1908)
Brouwer L.E.J.: Intuitionistische Betrachtungen ueber der Formels. In: Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, Amsterdam, vol. 31, pp. 374–379 (1927), also as 1927b paper in Brouwer L.E.J. [1975] Collected... , op. cit., pp. 409–417
Drago, A.: A.N. Kolmogoroff and the relevance of the double negation law in science. In: Sica, G. (ed.) Essays on the Foundations of Mathematics and Logic, pp. 57–81. Polimetrica, Milan (2005)
Drago, A.: Pluralism in logic: the square of opposition, Leibniz’ principle of sufficient reason and Markov’s principle. In: Béziau, J.-Y., Jacquette, D. (eds.) Around and Beyond the Square of Opposition, pp. 175–189. Basel, Birkhaueser (2012)
Drago, A.: A pluralist foundation of the mathematics of the first half of the twentieth century. J. Indian Counc. Philos. Res. 34(2), 343–363 (2017)
Drago, A.: Koyré’s revolutionary role in the historiography of science. In: Pisano, R., Agassi, J., Drozdova, D. (eds.) Hypotheses and Perspectives in the History and Philosophy of Science. Homage to Alexandre Koyré 1892–1964, pp. 123–141. Springer, Berlin (2017)
Dummett, M.: Elements of Intuitionism. Claredon University Press, Oxford (1977)
Heyting, A.: The formal rules of intuitionist logic. In: Mancosu, P. (ed.) (1998) From Hilbert to Goedel, pp. 311–325. Oxford University Press, Oxford (1930)
Heyting, A.: Die formalen Regeln der intuitionistischen Logik I, Sitzungsberichte der Preussischen Akademie der Wissenschaften, pp. 42–56. (English translation in Mancosu (1998), op. cit., pp. 311–327) (1930)
Kolmogorov, A.N.: On the principle ‘tertium non datur’. In: Mathematicheskii Sbornik, vol. 32, pp. 646–667 (Engl. transl. in van Heijenoorth J. (ed.) (1967), From Frege to Goedel. Cambridge MA: Harvard U.P., pp. 416–437) (1924/25)
Kolmogoroff, A.N.: Zur Deutung der Intuitionistischen Logik. Math. Zeitfr., vol. 35, pp. 58–65 (Engl. Transl. In Mancosu P. (1998), From Hilbert to Goedel, Oxford: Oxford U.P., 328–334) (1932)
Leibniz, G.W.: Letter to Arnaud, 14th July (1686)
Leibniz, G.W.: Theodicy. Routledge, London (1710)
Lobachevsky, N.I..: Geometrische Untersuchungen zur der Theorien der Parallellineen, Finkl, Berlin (English transl. as an Appendix to Bonola R., Non-Euclidean Geometry. Dover, New York, 1955)
Mancosu, P. (ed.): From Brouwer to Hilbert. The Debate on the Foundations of Mathematics in the 1920s. Oxford University Press, Oxford (1998)
Markov, A.A.: On Constructive Mathematics. Trudy Math. Inst. Steklov, 67, pp. 8–14; also in Am. Math. Soc. Translations, (1971) 98(2), pp. 1–9 (1962)
Martin-Loef, P.: The Hilbert–Brouwer controversy resolved? In: van Atten, M., Boldini, P., Bourdeau, M., Heinzmann, G. (eds.) One Hundred Years of Intuitionism (1907–2007), pp. 243–256. Birckhaueser, Basel (2008)
Moschovakis, J.: Intuitionist Logic. In: Zalta, E.N. (ed.) Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/logic-intuitionistic/ (2018)
Prawitz, D., Melmnaas, P.-E.: A survey of some connections between classical, intuitionistic and minimal logic. In: Schmidt, A., Schutte, K., Thiele, H.J. (eds.) Contributions to Mathematical Logic, pp. 215–229. North-Holland, Amsterdam (1968)
Raatakainen, P.: Conceptions of truth in intuitionism. History and Philosophy of Logic 25, 131–145 (2004)
Troelstra, A., van Dalen, D.: Constructivism in Mathematics. North-Holland, Amsterdam (1988)
Uspensky, V.A.: Kolmogorov and mathematical logic. J. Symb. Log. 57, 385–412 (1992)
Acknowledgements
I acknowledge Professor David Braithwhaite for the numerous corrections on my English text.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Drago, A. An Intuitionist Reasoning Upon Formal Intuitionist Logic: Logical Analysis of Kolmogorov’s 1932 Paper. Log. Univers. 15, 537–552 (2021). https://doi.org/10.1007/s11787-021-00292-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11787-021-00292-3
Keywords
- Two dichotomies
- Choices of Intuitionist logic
- Choices of Kolmogorov’s 1932 paper
- Structural foundation of intuitionist logic
- Intuitionist reasoning





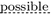 that…” is equivalent to “It is not true that it is not…”. This equivalence is confirmed by the S4 translation of model logic into IL These words will be pointwise underlined, while the two negative words of a DNP will be underlined continuously.
that…” is equivalent to “It is not true that it is not…”. This equivalence is confirmed by the S4 translation of model logic into IL These words will be pointwise underlined, while the two negative words of a DNP will be underlined continuously.