Abstract
This paper investigates behavior in finitely repeated simultaneous and sequential-move prisoner’s dilemma games when there is one-sided incomplete information and signaling about players’ concerns for fairness, specifically, their preferences regarding “inequity aversion.” In this environment, we show that only a pooling equilibrium can be sustained, in which a player type who is unconcerned about fairness initially cooperates in order to disguise himself as a player type who is concerned about fairness. This disguising strategy induces the uninformed player to cooperate in all periods of the repeated game, including the final period, at which point the player type who is unconcerned about fairness takes the opportunity to defect, i.e., he “backstabs” the uninformed player. Despite such last-minute defection, our results show that the introduction of incomplete information can actually result in a Pareto improvement under certain conditions. We connect the predictions of this “backstabbing” equilibrium with the frequently observed decline in cooperative behavior in the final period of finitely repeated experimental games.


Similar content being viewed by others
Notes
Players in PD games face similar strategic incentives as those in public good games and, more generally, games where players’ actions are strategic substitutes. Sequential-move versions are also used to characterize firm-worker wage-effort decisions and the notion of “gift-exchange.”
For instance, for the finitely repeated PD game, Andreoni and Miller’s (1993) experiment shows that cooperation peaks in the first round of interaction (86% of subjects cooperate), stays above 50% until round 6, and then falls to about zero in the last (tenth) round.
In particular, the worker’s type is assumed to be either reciprocator or selfish, since Healy’s results do not derive from any preference specification.
In particular, we examine a twice-repeated sequential-move PD game where the first mover is uninformed about the second mover’s social preferences. In this game, the first mover cooperates only when he believes that the second mover will reciprocate afterward (which occurs when the second mover is highly concerned about fairness). These strategic incentives coincide with those in the gift-exchange game analyzed by Healy (2007) whereby the firm manager only offers high wages when he believes that the worker is a reciprocating type.
In a study of the hold-up problem under incomplete contracts, Siemens (2009) considers a signaling game whereby the seller of a good initially invests in the good’s quality, and then the seller and a buyer interact in an ultimatum bargaining game where the buyer makes a take-it-or-leave-it offer to the seller. Similar to our results, his paper also shows that the seller’s initial investment can serve to conceal his privately observed fairness concerns to the buyer in order to condition the buyer’s offers in the ensuing bargaining.
In such a context, the uninformed player defects at every stage of the game and, therefore, the informed player cannot affect the uninformed player’s actions. This eliminates the possibility of information transmission; see Kreps et al. (1982), p. 251. If, in contrast, the model in Kreps et al. (1982) is modified to allow for one-sided uncertainty where it is common knowledge that reciprocation is a dominant strategy for the uninformed player, then both our model and theirs would yield a similar cooperative outcome. Such cooperation, nonetheless, originates from inequity aversion in our model (which has regularly been observed in experiments), while the irrational reciprocation in Kreps et al. (1982), i.e., which arises when their parameter \(a\) is lower than 1, would be more difficult to support experimentally.
We also consider the usual second condition on the parameters of PD games, \( 2a>b+c\), to guarantee that, in the iterative version of the game, mutual cooperation provides a larger payoff than that arising from alternating cooperation and defection.
Intuitively, \(\alpha _{i}\ge \beta _{i}\) implies that players (weakly) suffer more from inequality directed at them than inequality directed at others. Empirically, estimates of \(\alpha _i\) have been found to be 2–3 times higher than estimates of \(\beta _i\). On the other hand, \(\beta _{i}\ge 0\) means that players dislike being better off than others (this assumption rules out cases in which individuals are status seekers but serves to simplify the analysis). Finally, \(\beta _{i}<1\) suggests that when player \(i\)’s payoff is higher than that of player \(j\)’s by one unit (e.g., a dollar), player \(i\) is never willing to give up more than one unit in order to reduce this inequality. For more details, see Fehr and Schmidt (1999).
Note that this best response function is similar to what Cooper et al. (1996) call “best response altruists,” namely players for whom cooperate (defect) is their best response to cooperation (defection, respectively). This result also relates with that of Rabin (1993) for psychological games, where he assumes that players are motivated by the kindness they infer from other players’ actions. Rabin (1993) assumes, however, that individuals’ kindness parameters are common knowledge among the players. In contrast, we extend our study by allowing for incomplete information.
This best response function for the second mover resembles that of Falk and Fischbacher (2006). In particular, assuming that individuals are perfectly informed about each others’ reciprocal motivations, they show that the second mover might respond by “matching” the first mover’s choice if the second mover is sufficiently reciprocally motivated. When the second mover is insufficiently motivate to reciprocate, he responds to any action of the first mover with defection.
Clark and Sefton (2001) provide an experimental test of this best response function. Specifically, they modify the payoff structure in the sequential PD game so that the second mover can obtain a “temptation payoff” if he is the only player defecting. Note that this payoff structure resembles ours, since payoffs associated to the (C,C) and (D,D) outcomes are unmodified, relative to the standard PD game (with selfish players), but those in which only the second mover defects vary. In particular, they find that the second mover is more likely to respond to cooperation with cooperation as the “temptation payoff” from defecting decreases. This experimental observation is in line with our result, since the second mover has greater incentives to respond to cooperation with cooperation if his concerns for fairness are relatively high (when the “temptation payoff” from defecting decreases), but responds by defecting against any choice by the first mover when he (the second mover) is unconcerned about fairness (when the “temptation payoff” increases).
Otherwise, player \(j\) would find defection to be a strictly dominant strategy in the second-period simultaneous-move game, and the first-period player \(i\)’s actions would not affect player \(j\)’s future play.
In order to guarantee that the observation of envy parameter \(\alpha _{i}\) does not allow the uninformed player \(j\) to infer the guilt parameter \(\beta _{i}\), consider that \(\alpha _{i}\) is distributed according to a continuous distribution function \(G(\alpha _{i})\), which assigns a positive probability to all \(\alpha _{i}\ge \beta _{i}^\mathrm{H}\). In such setting, observing the precise realization of \(\alpha _{i}\) does not provide player \(j\) with any additional information about \(\beta _{i}\), other than that \(\beta _{i}\) must satisfy \(\alpha _{i}\ge \beta _{i}\), which holds by assumption. Note that if, instead, \(\alpha _{i}\) was distributed according to a discrete probability distribution by which \(\alpha _{i}\) could only take two possible values, the mere observation of the realization of \(\alpha _{i}\) would allow the uninformed player \(j\) to infer the value of \(\beta _{i}\), thus nullifying the signaling role of player \(i\)’s actions.
Therefore, the uninformed player \(j\) (being highly concerned about fairness) does not know whether the game he plays with player \(i\) is: (1) a Pareto coordination game, which arises when player \(i\) is also highly concerned about fairness; or (2) a game where defection is a strictly dominant strategy for player \(i\), while player \(j\) still prefers to mimic the action selected by his opponent, which ensues when player \(i\)’s concerns for fairness are low. Hence, the latter game can neither be interpreted as a standard PD game or as a Pareto coordination game.
For simplicity, we ignore discounting. However, for completeness at the end of this section we demonstrates that the equilibrium predictions of Proposition 1 are unaffected by allowing for discounting. In addition, note that we use “pooling” equilibrium to refer to strategy profiles in which both types of informed player \(i\) cooperate during the first-period game. For robustness, we show that this pooling equilibrium survives Cho and Kreps’ (1987) Intuitive Criterion; see Appendix 2. That appendix also provides conditions under which a “non-cooperative” pooling equilibrium—where both types of player \(i\) defect in the first period—can be sustained, and under which parameter values it survives Cho and Kreps’ (1987) Intuitive Criterion.
If players’ guilt parameters satisfied \(\beta _{i}^\mathrm{H}>\beta _{i}^\mathrm{L}\), but envy concerns were lower for those concerned about fairness than for unconcerned players, i.e., if \(\alpha _{i}^\mathrm{H}\le \alpha _{i}^\mathrm{L}\), then such a separating strategy profile could be sustained in equilibrium. However, following the experimental evidence by Bellemare et al. (2008) as described at the beginning of this section, we think it is more plausible to assume that individuals with high concerns for inequity aversion exhibit both larger guilt and envy concerns than players with low concerns, thus implying that this case will not arise.
If, instead, priors are sufficiently low, i.e., \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\), the uninformed player \(j\) defects in the first period of the game and, as a consequence, an alternative pooling equilibrium emerges in which the informed player \(i\) defects in the first period of interaction, both when he is concerned about fairness and when he is not. Player \(j\)’s action in the second-period of interaction, however, depends on his off-the-equilibrium beliefs: when they are relatively high, the uninformed player \(j\) chooses to cooperate after observing that player \(i\) cooperated in the first period, but defects otherwise. In such a setting, player \(i\) does not find it profitable to cooperate in the first-period game, thus leading both types of player \(i\) to defect. For more details about this pooling equilibrium, see Appendix 1.
If the simultaneous-move PD game is, instead, repeated for \(T>2\) periods, the informed player \(i\) becomes more attracted to cooperation, since his cooperation triggers a longer stream of cooperative outcomes, yielding an overall payoff that exceeds that from defecting under larger parameter conditions. Therefore, the pooling equilibrium can be sustained for less restrictive conditions as the number of repetitions increases.
For a detailed analysis of these conditions, see Appendix 3.
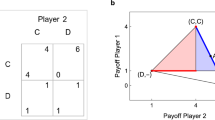
In order to facilitate our utility comparisons, we hereafter assume that, in settings where both outcomes (C,C) and (D,D) can be sustained in equilibrium as in the shaded area of Fig. 1 for the simultaneous-move PD game under complete information, players can resort to some coordination mechanism, such as social norms or a stochastic randomization, that enables them to coordinate on the efficient cooperative outcome (C,C). Alternatively, if a pre-play communication stage exists, Demicheli and Weibull (2008) show that, in the context of Pareto coordination games such as that arising when \(\beta _{i},\beta _{j}\ge \frac{b-a}{b-c}\) in our model, every evolutionary stable equilibrium induces players to asymptotically coordinate on the cooperative outcome (C,C).
In particular, this result corresponds to proposition 1 in Healy (2007) where the past actions of all players are observable, but workers’ types are not.
Note that, in the context of the simultaneous-move PD game, our equilibrium results in Sect. 5.1 would not be affected if we modified which player holds private information about his social preferences, either player 1 (the row player) or 2 (the column player), since our results in those propositions are valid for any player \(i=\{1,2\}\) and \(j\ne i\).
References
Anderhub, V., Engelmann, D., & Güth, W. (2002). An experimental study of the repeated trust game with incomplete information. Journal of Economic Behavior and Organization, 48(2), 197–216.
Andreoni, J., & Miller, J. H. (1993). Rational cooperation in the finitely repeated prisoner’s dilemma: Experimental evidence. The Economic Journal, 103, 570–585.
Banks, J. S., & Sobel, J. (1987). Equilibrium selection in signaling games. Econometrica, 55, 647–661.
Bellemare, C., Kröger, S., & van Soest, A. (2008). Measuring inequity aversion in a heterogeneous population using experimental decisions and subjective probabilities. Econometrica, 76, 815–839.
Bolle, F., & Ockenfels, P. (1990). Prisoner’s dilemma as a game with incomplete information. Journal of Economic Psychology, 11, 69–84.
Bolton, G. E., & Ockenfels, A. (2000). ERC: A theory of equity, reciprocity, and competition. American Economic Review, 90, 166–193.
Brandts, J., & Figueras, N. (2003). An exploration of reputation formation in experimental games. Journal of Economic Behavior and Organization, 50, 89–115.
Camerer, C., & Weigelt, K. (1988). Experimental tests of the sequential equilibrium reputation model. Econometrica, 56(1), 36.
Clark, K., & Sefton, M. (2001). The sequential prisoner’s dilemma: Evidence on reciprocation. The Economic Journal, 111, 51–68.
Cho, I.-K., & Kreps, D. (1987). Signaling games and stable equilibrium. Quarterly Journal of Economics, 102, 179–222.
Cooper, R., DeJong, D. V., Forsythe, R., & Ross, T. W. (1996). Cooperation without reputation: Experimental evidence from prisoner’s dilemma games. Games and Economic Behavior, 12, 187–218.
Demicheli, S., & Weibull, J. W. (2008). Language, meaning, and games: A model of communication, coordination, and evolution. American Economic Review, 98(4), 1292–1311.
Duffy, J., & Muñoz-García, F. (2012). Patience or fairness? Analyzing social preferences in repeated games. Games, 3(1), 56–77.
Falk, A., & Fischbacher, U. (2006). A theory of reciprocity. Games and Economic Behavior, 54, 293–315.
Fehr, E., & Schmidt, K. (1999). A theory of fairness, competition and cooperation. Quarterly Journal of Economics, 114, 817–868.
Fong, Y.-F. (2009). Private information of nonpaternalistic altruism: Exaggeration and reciprocation of generosity. The B.E. Journal of Theoretical Economics, 9, article 1.
Healy, P. J. (2007). Group reputations, stereotypes, and cooperation in a repeated labor market. American Economic Review, 97(5), 1751–1773.
Kreps, D., & Wilson, R. (1982). Reputation and imperfect information. Journal of Economic Theory, 27, 253–279.
Kreps, D., Milgrom, P., Roberts, J., & Wilson, R. (1982). Rational cooperation in the finitely repeated prisoners’ dilemma. Journal of Economic Theory, 27, 245–252.
McKelvey, R. D., & Palfrey, T. R. (1992). An experimental study of the centipede game. Econometrica, 60, 803–836.
Rabin, M. (1993). Incorporating fairness into game theory and economics. American Economic Review, 83(5), 1281–1302.
Selten, R., & Rolf, S. (1986). End behavior in sequences of finite prisoner’s dilemma supergames. A learning theory approach. Journal of Economic Behavior and Organization, 7(1), 47–70.
von Siemens, F. (2009). Bargaining under incomplete information, fairness, and the hold-up problem. Journal of Economic Behavior and Organization, 71, 486–494.
Author information
Authors and Affiliations
Corresponding author
Additional information
We thank the editor and six referees for helpful comments and suggestions on an earlier draft of this paper.
Appendices
Appendix 1: Noncooperative pooling equilibria
Proposition 3
A pooling PBE can be sustained in which player \(i\) defects in the first period both when he is concerned about fairness and when he is not, and:
-
a.
Player \(i\) defects in the second period, both when he is concerned about fairness and when he is not. The uninformed player \(j\) defects in the first and second period, regardless of player i’s choices during the first stage, given beliefs \(\mu (\beta _{i}^\mathrm{H}|D) =q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\) and \(\mu (\beta _{i}^\mathrm{H}|C) <q^\mathrm{Sim}(\alpha _{j},\beta _{j})\); and
-
b.
Player \(i\) defects in the second period when he is unconcerned about fairness, but cooperates in equilibrium otherwise given \(\alpha _{i}^\mathrm{H}\ge \frac{a+c-2d}{b-c}\) and \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}\ge \frac{c+b-2b}{b-c}\). The uninformed player \(j\) defects in the first period. In the second period, player \(j\) defects after observing that player \(i\) defects in the first period but cooperates otherwise, given beliefs \(\mu (\beta _{i}^\mathrm{H}|D) =q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})<\mu (\beta _{i}^\mathrm{H}|C)\).
-
c.
Player \(i\) defects in the second period when he is concerned about fairness, but cooperates in equilibrium otherwise given \( \frac{b-a}{b-c}\le \beta _{i}^\mathrm{H}<\frac{b-d}{b-c}\). The uninformed player \(j\) cooperates in the first period. In the second period, player \(j\) cooperates after observing that player \(i\) defects in the first period but defects otherwise, given beliefs \(\mu \left( \beta _{i}^\mathrm{H}|D\right) =q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})>\mu \left( \beta _{i}^\mathrm{H}|C\right) \).
Proof
Let us investigate the pooling equilibrium in which both types of informed player \(i\) defect in the first period of the game. First, note that after observing an action from player \(i\) in the first period, player \(j\)’s beliefs in this pooling equilibrium are \(\mu (\beta _{i}^\mathrm{H}|C)\equiv \mu \in [0,1]\) and \(\mu (\beta _{i}^\mathrm{H}|D)=q\). Given these beliefs, let us now analyze player \(j\)’s best response in the second period of the game. In particular, after observing a D choice in the first period (in equilibrium), player \(j\) cannot infer player \(i\)’s social preferences and must therefore make her second period choice according to an expected utility comparison. In particular, player \(j\) cooperates in the second period if
That is, if \(q\ge \frac{d-c+\alpha _{j}(b-c)}{a+d-c-b+(\alpha _{j}+\beta _{j})(b-c)}\equiv q^\mathrm{Sim}(\alpha _{j},\beta _{j})\). Note that this cutoff strategy coincides with the one he uses when choosing between C and D at the beginning of the first period. After observing C being played in the first-period stage game (which occurs off-the-equilibrium) player \(j\) cannot infer player \(i\)’s social preferences either, and must therefore choose C or D in the second period according to an expected utility comparison. Specifically, player \(j\) cooperates in the second period if and only if
That is, if \(\mu \ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\). Let us now investigate the informed player \(i\)’s actions during the first period:
-
1.
If \(q,\mu \ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\) player \(j\) cooperates in the first period of the game, as well as in the second period, both after observing that player \(i\) selects C and D. The highly concerned player \(i\) cooperates given that \(a+a\ge b-\beta _{i}^\mathrm{H}(b-c)+a\), which holds since \( \beta _{i}^\mathrm{H}\ge \frac{b-a}{b-c}\) by definition. Hence, the prescribed strategy profile cannot be supported as a pooling PBE if \(q,\mu \ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\).
-
2.
If \(q,\mu <q^\mathrm{Sim}(\alpha _{j},\beta _{j})\) player \(j\) defects in the first period of the game, as well as in the second period, both after observing that player \(i\) selects C and D. On the one hand, the highly concerned player \(i\) defects if \(c-\alpha _{i}^\mathrm{H}(b-c)+d\le d+d\), which implies \(\alpha _{i}^\mathrm{H}\ge 0>\frac{c-d}{b-c}\), which holds by definition. On the other hand, the unconcerned player \(i\) defects if \( c-\alpha _{i}^\mathrm{L}(b-c)+d\le d+d\), which implies \(\alpha _{i}^\mathrm{L}\ge 0> \frac{c-d}{b-c}\), which also holds by definition. Therefore, this pooling strategy profile can be sustained as a PBE if \(q,\mu <q^\mathrm{Sim}(\alpha _{j},\beta _{j})\); as described in Proposition 3(a).
-
3.
If \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})>\mu \) player \(j\) cooperates in the first period of the game, as well as in the second period but only if he observes that player \(i\) chose D in the first period. On the one hand, the highly concerned player \(i\) defects if \(a+d\le b-\beta _{i}^\mathrm{H}(b-c)+a\), which is satisfied if \(\beta _{i}^\mathrm{H}\le \frac{b-d}{b-c}\), where \(\frac{ b-a}{b-c}\le \beta _{i}^\mathrm{H}\le \frac{b-d}{b-c}\). On the other hand, the unconcerned player \(i\) defects if \(a+d\le b-\beta _{i}^\mathrm{L}(b-c)+b-\beta _{i}^\mathrm{L}(b-c)\), which holds if \(\beta _{i}^\mathrm{L}<\frac{2b-a-d}{2(b-c)}\), which is satisfied since \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}<\frac{2b-a-d}{2(b-c)}\). Hence, this pooling strategy profile can be supported as PBE if \(\frac{b-a}{ b-c}\le \beta _{i}^\mathrm{H}\le \frac{b-d}{b-c}\) and \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})>\mu \); as described in Proposition 3(c).
-
4.
If \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\le \mu \) player \(j\) defects in the first period of the game, as well as in the second period but only if he observes that player \(i\) chose C in the first period. On the one hand, the informed highly concerned player \(i\) defects if \(c-\alpha _{i}^\mathrm{H}(b-c)+a\le d+d\), or \(\alpha _{i}^\mathrm{H}\ge \frac{a+c-2d}{b-c}\), where \(\frac{a+c-2d}{b-c}>\frac{b-a}{b-c}\) if \((b-c)<2(a-d)\). On the other hand, the unconcerned player \(i\) defects if \(c-\alpha _{i}^\mathrm{L}(b-c)+b-\beta _{i}^\mathrm{L}(b-c)\le d+d\), or \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}\ge \frac{c+b-2d}{ b-c}\). Therefore, the prescribed strategy profile can be sustained as a pooling PBE if \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\le \mu \), the social preference parameters of the highly concerned player \(i\) satisfy \(\alpha _{i}^\mathrm{H}\ge \frac{a+c-2d}{b-c}\) and those of the relatively unconcerned player \(i\) satisfy \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}\ge \frac{c+b-2d}{b-c}\); as described in Proposition 3(b). \(\square \)
In the pooling equilibrium in which both types of player \(i\) defect (part a of Proposition 3), the uninformed player \(j\)’s beliefs are so “pessimistic” that he chooses to defect in the second stage of the game, regardless of player \(i\)’s choices in the first period. Consequently, player \(i\) defects, both when he is concerned and when he is unconcerned about fairness. The strategy profile in part (b) describes a similar pooling equilibrium to that in part (a), but in which player \(j\)’s off-the-equilibrium-path beliefs are sufficiently high to induce him to cooperate after observing cooperation. Thus, player \(i\)’s choice induces player \(j\) to cooperate after observing cooperation but to defect otherwise. Consequently, deviating toward cooperation becomes a more attractive option than in part (a), where all actions are responded to with defection in the second period. In order to support the pooling equilibrium where both types of player \(i\) defect, the gain that player \(i\) obtains from second-period cooperation cannot offset the disutility from envy experienced from cooperating in the first period, yielding outcome (C,D). In particular, we require \(\alpha _{i}^\mathrm{H}\ge \frac{a+c-2d}{b-c}\) and \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}\ge \frac{c+b-2b}{b-c}\). Finally, in the pooling equilibrium described in part (c), the uninformed player \(j\) interprets a deviation toward cooperation as most likely originating from an unconcerned player \(i\), i.e., \(\mu (\beta _{i}^\mathrm{H}|C) <q^\mathrm{Sim}(\alpha _{j},\beta _{j})\), which are rather “insensible” off-the-equilibrium beliefs. Appendix 2 confirms this suspicion by showing that the pooling equilibrium in part (c) does not survive Cho and Kreps’ (1987) Intuitive Criterion. By contrast, we demonstrate that all other equilibria survive this refinement criterion.
Appendix 2: Equilibrium refinement
Lemma 2
The pooling PBE described in Proposition 1 survives Cho and Kreps’ (1987) Intuitive Criterion under all parameter values. All PBEs in Proposition 3 (Appendix 1) also survive the Intuitive Criterion, except for the pooling equilibrium described in part (c).
Proof
Proposition 1. Let us first check whether the pooling PBE where both types of player \(i\) cooperate in the first period under \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\) survives the Intuitive Criterion. Regarding the unconcerned player \(i\), if he deviates toward defection, the highest utility he can obtain is \(b-\beta _{i}^\mathrm{L}(b-c)+b-\beta _{i}^\mathrm{L}(b-c)\), which exceeds his equilibrium utility of \(a+b-\beta _{i}^\mathrm{L}(b-c)\). Regarding the highly concerned player \(i\), if he deviates to defection, the highest utility he can obtain is \(a+a\), which coincides with his equilibrium utility from cooperating. Hence, only the unconcerned player \(i\) has incentives to deviate toward defection, allowing the uninformed player \(j\) to restrict his posterior beliefs to \(\mu (\beta _{i}^\mathrm{H}|D)=0\). Hence, a defection can only originate from an unconcerned player \(i\), inducing player \(j\) to defect in the second-period stage game, yielding a total utility for the unconcerned player \(i\) of \(b-\beta _{i}^\mathrm{L}(b-c)+d\), which does not exceed his equilibrium utility given that \( a+b-\beta _{i}^\mathrm{L}(b-c)\ge b-\beta _{i}^\mathrm{L}(b-c)+d\) since \(a\ge d\). Hence, no type of player \(i\) wants to deviate from the pooling PBE where both types cooperate, and therefore this pooling equilibrium survives the Intuitive Criterion.
Proposition 3, part a. Let us now check whether the pooling equilibrium in which both types of player \(i\) defect under \(q,\mu <q^\mathrm{Sim}(\alpha _{j},\beta _{j})\) survives the Intuitive Criterion. Regarding the highly concerned player \(i\), if he deviates toward cooperation the highest utility he can obtain is \(c-\alpha _{i}^\mathrm{H}(b-c)+a\), which exceeds his equilibrium utility of \(d+d\) if \(\alpha _{i}^\mathrm{H}<\frac{ a+c-2d}{b-c}\). [Recall that condition \(\alpha _{i}^\mathrm{H}<\frac{a+c-2d}{b-c}\) is compatible with the initial assumption of \(\beta _{i}^\mathrm{H}\ge \frac{b-a}{ b-c}\) if \(b-c<2(a-d)\)]. Regarding the unconcerned player \(i\), if he deviates toward cooperation the highest utility he can obtain is \(c-\alpha _{i}^\mathrm{L}(b-c)+b-\beta _{i}^\mathrm{L}(b-c)\), which exceeds his equilibrium utility of \(d+d\) only if \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}<\frac{c+b-2d}{b-c}\). Using the conditions we found for the concerned and unconcerned player \(i\), let us examine under which cases this pooling equilibrium survives the Intuitive Criterion:
-
1.
When both \(\alpha _{i}^\mathrm{H}<\frac{a+c-2d}{b-c}\) and \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}<\frac{c+b-2d}{b-c}\) hold, both types of player \(i\) have incentives to deviate, and the uninformed player \(j\) cannot restrict his beliefs upon observing a deviation to cooperation (off-the-equilibrium). As a consequence, no type of player \(i\) has incentives to modify his equilibrium action, and hence this pooling equilibrium survives the Intuitive Criterion.
-
2.
When condition \(\alpha _{i}^\mathrm{H}<\frac{a+c-2d}{b-c}\) holds but \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}<\frac{c+b-2d}{b-c}\) does not, the concerned player \( i \) has incentives to deviate toward cooperation but the unconcerned type does not. Conditions \(\alpha _{i}^\mathrm{H}<\frac{a+c-2d}{b-c}\) and \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}>\frac{c+b-2d}{b-c}\), however, are incompatible with the initial assumption of \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\). (In particular, combining \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}\ge \frac{c+b-2d}{b-c}\) with the assumption of \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\), we obtain that \(\alpha _{i}^\mathrm{L}\) must satisfy \(\alpha _{i}^\mathrm{L}\ge \frac{a+c-2d}{b-c}\). This result is, however, incompatible with condition \(\alpha _{i}^\mathrm{H}<\frac{a+c-2d}{b-c}\) that we obtained for the concerned player \(i\) since, by definition, envy concerns must satisfy \(\alpha _{i}^\mathrm{H}>\alpha _{i}^\mathrm{L}\).) Hence, these parameter combinations are not feasible.
-
3.
When neither condition \(\alpha _{i}^\mathrm{H}<\frac{a+c-2d}{b-c}\) nor \( \alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}<\frac{c+b-2d}{b-c}\) hold, then neither type of player \(i\) has incentives to deviate. Consequently, the uninformed player \(j\) cannot restrict his off-the-equilibrium beliefs, and no type of player \( i \) has incentives to change his equilibrium behavior. Therefore, this pooling equilibrium survives the Intuitive Criterion.
-
4.
When condition \(\alpha _{i}^\mathrm{H}<\frac{a+c-2d}{b-c}\) does not hold but \( \alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}<\frac{c+b-2d}{b-c}\) does, the concerned player \(i\) does not have incentives to deviate toward cooperation but the unconcerned player \(i\) does. Therefore, the uninformed player \(j\) restricts his off-the-equilibrium beliefs to \(\mu (\beta _{i}^\mathrm{H}|C)=0\) and \(\mu (\beta _{i}^\mathrm{H}|D)=1\), since cooperation can only originate from the unconcerned player \(i\). Consequently, player \(j\) cooperates in the second period after observing D but defects after observing C. Conditional on this response by player \(j\), the highly concerned player \(i\) does not have incentives to deviate toward cooperation since he would obtain \(c-\alpha _{i}^\mathrm{H}(b-c)+d\), which does not exceed his equilibrium utility of \(d+d\). Similarly, the unconcerned player \(i\) does not have incentives to deviate toward cooperation, since he would obtain \(c-\alpha _{i}^\mathrm{L}(b-c)+d\), which is lower than his equilibrium utility of \(d+d\). Hence, the pooling PBE in which both types of player \(i\) defect when \(q,\mu <q^\mathrm{\mathrm Sim}(\alpha _{j},\beta _{j})\) survives the Intuitive Criterion if \(\alpha _{i}^\mathrm{H}\ge \frac{a+c-2d }{b-c}\) and \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}<\frac{c+b-2d}{b-c}\).
Proposition 3, part b. Let us now examine the pooling equilibrium in which both types of player \(i\) defect under \(\mu \ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})>q\). Regarding the highly concerned player \(i\), if he deviates toward cooperation the highest utility he can obtain is \(c+\alpha _{i}^\mathrm{H}(b-c)+a\), which exceeds his equilibrium utility of \(d+d\) only if \( \alpha _{i}^\mathrm{H}<\frac{a+c-2d}{b-c}\), which violates the equilibrium conditions. Hence, the highly concerned player \(i\) does not have incentives to deviate. Regarding the unconcerned player \(i\), if he deviates toward cooperation the highest utility he can obtain is \(c+\alpha _{i}^\mathrm{L}(b-c)+b-\beta _{i}^\mathrm{L}(b-c)\), which exceeds his equilibrium utility of \(d+d\) only if \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}<\frac{c+b-2d}{b-c}\), which violates the equilibrium conditions. Therefore, the unconcerned player \(i\) does not deviate toward cooperation either. Since no type of player \(i\) deviates from his equilibrium action, player \(j\)’s posterior beliefs are unmodified, and this pooling PBE survives the Intuitive Criterion if \(\mu >q^\mathrm{Sim}(\alpha _{j},\beta _{j})>q\).
Proposition 3, part c. Let us finally examine the pooling equilibrium in which both types of player \(i\) defect under \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})>\mu \). Regarding the highly concerned player \(i\), if he deviates toward cooperation, the highest utility he can obtain is \(a+a\), which exceeds his equilibrium utility of \(b-\beta _{i}^\mathrm{H}(b-c)+a\) since \(\beta _{i}^\mathrm{H}\ge \frac{b-a}{b-c}\) by definition. Hence, the highly concerned player has incentives to deviate. Regarding the unconcerned player \(i\), if he deviates toward cooperation, the highest utility he can achieve is \(a+b-\beta _{i}^\mathrm{L}(b-c)\), which does not exceed his equilibrium utility of \(b-\beta _{i}^\mathrm{L}(b-c)+b-\beta _{i}^\mathrm{L}(b-c)\) since \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\). Therefore, only the concerned player \(i\) has incentives to deviate toward cooperation. Hence, the uninformed player \(j\) can restrict his off-the-equilibrium path beliefs after observing cooperation to \(\mu (\beta _{i}^\mathrm{H}|C)=1\), inducing him to cooperate in the second-period game as a consequence. Thus, the concerned player \(i\) obtains a higher utility by deviating from his equilibrium action of defection toward cooperation, and consequently, the pooling equilibrium in which both types of player \(i\) defect under \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})>\mu \) violates the Intuitive Criterion. Finally, note that since we consider just two types of privately informed player \(i\), who are either “concerned” or “unconcerned” about fairness, the application of Cho and Kreps’ Intuitive Criterion and Banks and Sobel’s (1987) Universal Divinity criterion (also referred to as the D1-Criterion) would lead to the same equilibrium predictions. \(\square \)
Appendix 3: Role of discounting
Separating equilibrium. Let us first analyze the separating strategy profile in which the highly concerned player \(i\) cooperates but the unconcerned player \(i\) defects. First, note that the uninformed player \(j\)’s beliefs and best response in the second-period game coincide with that given in Proposition 1, since he does not need to consider discounting in this case. In the first period of the game, however, player \(j\) selects C or D based on his expected utility, thus cooperating if and only if
or \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\). As in the proof of Proposition 1, let us now investigate the informed player \(i\)’s action during the first-period stage game:
-
1.
If \(q>q^\mathrm{Sim}(\alpha _{j},\beta _{j})\), the uninformed player \(j\) cooperates during the first period. On the one hand, the highly concerned player \(i\) thus cooperates if \(a+\delta a\ge b-\beta _{i}^\mathrm{H}(b-c)+\delta d\) , since cooperation (defection) is responded to with cooperation (defection, respectively) in the subsequent period. Solving for \(\beta _{i}^\mathrm{H}\), we obtain that player \(i\) cooperates if \(\beta _{i}^\mathrm{H}\ge \frac{b-\delta d-a(1+\delta )}{b-c}\). And since \(\beta _{i}^\mathrm{H}\ge \frac{b-a}{b-c}>\frac{ b-d-2a}{b-c}>\frac{b-\delta d-a(1+\delta )}{b-c}\) by definition, the above condition is satisfied, implying that the highly concerned player \(i\) cooperates in the first period, as prescribed in this separating strategy profile. On the other hand, the unconcerned player \(i\) cooperates if \( a+\delta [ b-\beta _{i}^\mathrm{L}(b-c)]\ge [b-\beta _{i}^\mathrm{L}(b-c)]+\delta d\), which simplifies to \(\delta \ge \frac{a-[ b-\beta _{i}^\mathrm{L}(b-c)] }{d-[ b-\beta _{i}^\mathrm{L}(b-c)] }\). However, since \(a-[b-\beta _{i}^\mathrm{L}(b-c)]< 0\) because \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\), and \(d-[ b-\beta _{i}^\mathrm{L}(b-c)] >0\) since \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}<\frac{b-d}{b-c}\), then ratio \(\frac{a- [b-\beta _{i}^\mathrm{L}(b-c)] }{d-[b-\beta _{i}^\mathrm{L}(b-c)] } <0\), implying that the condition on the discount factor \(\delta \ge \frac{a- [b-\beta _{i}^\mathrm{L}(b-c)] }{d-[b-\beta _{i}^\mathrm{L}(b-c)]} \) holds for all \(\delta \in [0,1]\). Hence, the unconcerned player \(i\) also cooperates in the first period, which violates the above separating strategy profile.
-
2.
If \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\), the uninformed player \(j\) defects during the first period. On the one hand, the highly concerned player \(i\) cooperates if \(c-\alpha _{i}^\mathrm{H}(b-c)+\delta a\ge d+\delta d\), or \(\alpha _{i}^\mathrm{H}\le \frac{\delta a+c-d(1+\delta )}{b-c}\); note that this cutoff is higher than \(\frac{b-a}{b-c}\) if and only if \(a>\frac{d(1+\delta )+b-c}{1+\delta }\). On the other hand, the unconcerned player \(i\) defects if \(c-\alpha _{i}^\mathrm{L}(b-c)+\delta \left[ b-\beta _{i}^\mathrm{L}(b-c)\right] \le d+\delta d\), which implies \(\alpha _{i}^\mathrm{L}\ge \frac{c+b(1-\beta _{i}^\mathrm{L})\delta +c\delta \beta _{i}^\mathrm{L}-d(1+\delta )}{b-c}\). Therefore, for a separating equilibrium to exist in which player \(i\) cooperates if and only if he is highly concerned about fairness, prior probability \(q\) must satisfy \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\), envy must satisfy \(\alpha _{i}^\mathrm{H}\le \frac{\delta a+c-d(1+\delta )}{b-c}\), and \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}\ge \frac{c+b(1-\beta _{i}^\mathrm{L})\delta +c\delta \beta _{i}^\mathrm{L}-d(1+\delta )}{b-c}\). The initial assumption \(\beta _{i}^\mathrm{L}<\frac{ b-a}{b-c}\) and condition \(\alpha _{i}^\mathrm{L}\ge \frac{c+b(1-\beta _{i}^\mathrm{L})\delta +c\delta \beta _{i}^\mathrm{L}-d(1+\delta )}{b-c}\), however, are incompatible with \(\alpha _{i}^\mathrm{H}\le \frac{\delta a+c-d(1+\delta )}{b-c}\). (In particular, combining \(\alpha _{i}^\mathrm{L}\ge \frac{c+b(1-\beta _{i}^\mathrm{L})\delta +c\delta \beta _{i}^\mathrm{L}-d(1+\delta )}{b-c}\) with the assumption of \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\), we obtain that \(\alpha _{i}^\mathrm{L}\) must satisfy \(\alpha _{i}^\mathrm{L}\ge \frac{\delta a+c-d(1+\delta )}{ b-c}\). This result is, however, incompatible with condition \(\alpha _{i}^\mathrm{H}\le \frac{\delta a+c-d(1+\delta )}{b-c}\) that we obtained for the concerned player \(i\) since, by definition, envy concerns must satisfy \( \alpha _{i}^\mathrm{H}>\alpha _{i}^\mathrm{L}\).) As a consequence, this separating strategy profile cannot be sustained as a PBE of the game.
Pooling equilibrium. Let us analyze the pooling strategy profile where both types of informed player \(i\) cooperate in the first period of the game. Beliefs coincide with those in the pooling equilibrium of Proposition 1, i.e., \(\mu (\beta _{i}^\mathrm{H}|C)=q\) (in equilibrium) and \(\mu (\beta _{i}^\mathrm{H}|D)\equiv \gamma \in [0,1]\) (off-the-equilibrium path). Given these beliefs, the uninformed player \(j\) cannot infer anything about the type of player \(i\) after observing that player \(i\) chose C in the first period (in equilibrium) and must therefore select C or D in the second period according to an expected utility comparison similar to that given in the proof of Proposition 1. Specifically, player \(j\) cooperates in the second-period PD game if and only if
That is, if \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\). Similarly, in the first-period stage game, player \(j\) is uninformed about player \(i\)’s concern for fairness, and hence chooses to cooperate in the first-period PD game according to the same cutoff strategy that conditions on the prior probability that player \(i\)’s type is high. After observing that player \(i\) selected D in the first-period stage game (off-the-equilibrium path behavior) player \(j\) cannot infer player \(i\)’s social preferences either, and must therefore select C or D in the second period of the game according to an expected utility comparison. Specifically, player \(j\) cooperates in the second period if and only if
That is, if \(\gamma \ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\). Let us now investigate the informed player \(i\)’s actions during the first-period stage game:
-
1.
If \(q,\gamma \ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\) player \(j\) cooperates in both the first and second periods of the game, both after observing that player \(i\) selects C and D. On the one hand, the highly concerned player \(i\) cooperates if \(a+\delta a\ge b-\beta _{i}^\mathrm{H}(b-c)+\delta a\), which holds since \(\beta _{i}^\mathrm{H}\ge \frac{b-a}{b-c }\) by definition. On the other hand, the unconcerned player \(i\) defects since \(a+\delta [b-\beta _{i}^\mathrm{L}(b-c)] \le b-\beta _{i}^\mathrm{L}(b-c)+\delta [b-\beta _{i}^\mathrm{L}(b-c)]\), which holds given that \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\). Therefore, this pooling strategy profile cannot be supported if \(q,\gamma \ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\).
-
2.
If \(q,\gamma <q^\mathrm{Sim}(\alpha _{j},\beta _{j})\) player \(j\) defects both in the first and second periods of the game, both after observing that player \(i\) selects C and D. The highly concerned player \(i\) defects, however, since \(c-\alpha _{i}^\mathrm{H}(b-c)+\delta d\le d+\delta d\), which implies \(\alpha _{i}^\mathrm{H}\ge 0\ge \frac{c-d}{b-c}\), which holds by definition. Hence, this pooling strategy profile cannot be sustained if \(q,\gamma <q^\mathrm{Sim}(\alpha _{j},\beta _{j})\).
-
3.
If \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})>\gamma \) player \(j\) cooperates in the first period of the game and in the second period he cooperates only after observing that player \(i\) chose C in the first-period stage game. On the one hand, the highly concerned player \(i\) cooperates since \(a+\delta a\ge b-\beta _{i}^\mathrm{H}(b-c)+\delta d\), or \(\beta _{i}^\mathrm{H}\ge \frac{b+\delta d-a(1+\delta )}{b-c}\). Given that \(\frac{b-a}{b-c }>\frac{b+d-2a}{b-c}>\frac{b+\delta d-a(1+\delta )}{b-c}\) for all \(\delta \in [0,1]\), then condition \(\beta _{i}^\mathrm{H}\ge \frac{b+\delta d-a(1+\delta )}{b-c}\) is satisfied from the assumption \(\beta _{i}^\mathrm{H}\ge \frac{b-a}{b-c}\). On the other hand, the unconcerned player \(i\) cooperates if \(a+\delta \left[ b-\beta _{i}^\mathrm{L}(b-c)\right] \ge b-\beta _{i}^\mathrm{L}(b-c)+\delta d\), or \(\beta _{i}^\mathrm{L}\ge \frac{a-b(1-\delta )-d\delta }{(b-c)(\delta -1)}\). Moreover, since \(\frac{b-a}{b-c}>\frac{a-b(1-\delta )-d\delta }{(b-c)(\delta -1)}\), then the initial condition on this unconcerned player \(i\), \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\), implies that for all \(\beta _{i}^\mathrm{L}\in \left[ \frac{a-b(1-\delta )-d\delta }{(b-c)(\delta -1) },\frac{b-a}{b-c}\right) \) this type of player \(i\) also cooperates, and this pooling strategy profile can be supported as a PBE for \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})>\gamma \). (As a remark, notice that the length of the interval of values for \(\beta _{i}^\mathrm{L}\) for which the pooling equilibrium can be sustained, \(\frac{b-a}{b-c}-\frac{a-b(1-\delta )-d\delta }{(b-c)(\delta -1)}=\frac{(a-d)\delta }{\left( b-c\right) (1-\delta )}\), collapses to zero when \(\delta \rightarrow 0\), but becomes infinite (i.e., the pooling equilibrium can be supported for all values of \(\beta _{i}^\mathrm{L}\)) when \(\delta \rightarrow 1\).
-
3.
If \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\le \gamma \) player \(j\) defects in the first period of the game and in the second period he defects only after observing that player \(i\) selected C in the first-period stage game. The highly concerned player \(i\) defects, however, since \(c-\alpha _{i}^\mathrm{H}(b-c)+\delta a\le d+\delta a\), which implies \(\alpha _{i}^\mathrm{H}\ge 0\ge \frac{c-d}{b-c}\), which is satisfied by definition. Thus, this pooling strategy profile cannot be sustained if \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\le \gamma \). \(\square \)
1.1 Proof of Lemma 1
From the text we know that the best response of the second mover (player \( j \)) is to select the same action as the first mover when \(\beta _{j}\ge \frac{b-a}{b-c}\), but to defect when \(\beta _{j}<\frac{b-a}{b-c}\), regardless of the action selected by the first mover. Formally, for any action \(a_{i}\) that the first mover selects, the second mover’s best response function is:
When the second mover’s fairness concerns satisfy \(\beta _{j}\ge \frac{b-a}{ b-c}\), the second mover responds by selecting the action chosen by the first mover. Therefore, the first mover’s payoff from cooperating (which is responded to with cooperation) is \(a\), while that from defecting (which is responded to with defection) is \(d\). Since \(a>d\) by definition, the first mover prefers to cooperate when the second mover’s concerns about fairness satisfy \(\beta _{j}\ge \frac{b-a}{b-c}\), for any preference parameters of the first mover.
When, instead, the second mover’s fairness concerns satisfy \(\beta _{j}< \frac{b-a}{b-c}\), the second mover responds by defecting, regardless of the action previously selected by the first mover. In this case, if the first mover selects cooperation his utility is \(c-\alpha _{i}(b-c)\), while if he defects his payoff is \(d\). Since \(c-\alpha _{i}(b-c)<d\) for any \(\alpha _{i}\ge 0\), the first mover defects when the second mover’s fairness concerns satisfy \(\beta _{j}<\frac{b-a}{b-c}\). \(\square \)
1.2 Proof of Proposition 1
Separating equilibrium. Let us first analyze the separating strategy profile in which the highly concerned player \(i\) cooperates but the unconcerned player \(i\) defects. First, note that after observing an action from player \(i\) in the first period of the game, player \(j\)’s beliefs in this separating strategy profile are updated to \(\mu (\beta _{i}^\mathrm{H}|C)=1\) and \(\mu (\beta _{i}^\mathrm{H}|D)=0\). Given these beliefs, let us now analyze player \(j\)’s best response in the second period of the game. In particular, after observing C in the first period, the uninformed player \(j\) believes that his opponent, \(i,\) is a highly concerned type (so that \(i\) will continue to select C in the second-period stage game). Since player \(j\) is highly concerned about fairness, \(\beta _{j}\ge \frac{b-a}{b-c},\) it follows that \(a>b-\beta _{j}(b-c)\) and so the uninformed player \(j\) will choose to cooperate in the second period of game. However, after observing a D in the first period, the uninformed player \(j\) believes that his opponent is an unconcerned type who will choose D. Given that \(d>c-\alpha _{j}(b-c)\) by definition, the uninformed player \(j\) will choose to defect in the second-period stage game. Let us now examine the first period of the game. In the first period, the uninformed player \(j\) must select C or D based upon an expected utility comparison; specifically, \(j\) cooperates in the first period of the twice-repeated PD game if and only if:
That is, if \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\). Let us now investigate the informed player \(i\)’s action during the first-period stage game:
-
1.
If \(q>q^\mathrm{Sim}(\alpha _{j},\beta _{j})\), the uninformed player \(j\) cooperates during the first period. On the one hand, the highly concerned player \(i\) thus cooperates if \(a+a\ge b-\beta _{i}^\mathrm{H}(b-c)+d\), since cooperation (defection) is responded to with cooperation (defection, respectively) in the subsequent period. Solving for \(\beta _{i}^\mathrm{H}\), we obtain that player \(i\) cooperates if \(\beta _{i}^\mathrm{H}\ge \frac{b-d-2a}{b-c}\) . Further, since \(\beta _{i}^\mathrm{H}\ge \frac{b-a}{b-c}>\frac{b-d-2a}{b-c}\) by definition, the above condition is satisfied, implying that the highly concerned player \(i\) cooperates in the first period, as prescribed in this separating strategy profile. On the other hand, the unconcerned player \( i\) cooperates since \(a+[b-\beta _{i}^\mathrm{L}(b-c)]\ge [b-\beta _{i}^\mathrm{L}(b-c)]+d\), which holds given that \(a\ge d\). Hence, the unconcerned player \(i\) also cooperates in the first period, which violates the above separating strategy profile.
-
2.
If \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\), the uninformed player \(j\) defects during the first period. On the one hand, the highly concerned player \(i\) cooperates if \(c-\alpha _{i}^\mathrm{H}(b-c)+a\ge d+d\), or \(\alpha _{i}^\mathrm{H}\le \frac{a+c-2d}{b-c}\); note that this cutoff is higher than \( \frac{b-a}{b-c}\) if and only if \(b-c<2(a-d)\). On the other hand, the unconcerned player \(i\) defects if \(c-\alpha _{i}^\mathrm{L}(b-c)+b-\beta _{i}^\mathrm{L}(b-c)\le d+d\), which implies that \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}\ge \frac{c+b-2d}{b-c}.\) Therefore, for a separating equilibrium to exist in which player \(i\) cooperates if and only if he is highly concerned about fairness, the prior probability \(q\) must satisfy \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\), envy concerns must satisfy \(\alpha _{i}^\mathrm{H}\le \frac{ a+c-2d}{b-c}\), and \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}\ge \frac{c+b-2d}{b-c}\). The initial assumption that \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\) and the condition \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}\ge \frac{c+b-2d}{b-c}\), however, are incompatible with \(\alpha _{i}^\mathrm{H}\le \frac{a+c-2d}{b-c}\). (In particular, combining \(\alpha _{i}^\mathrm{L}+\beta _{i}^\mathrm{L}\ge \frac{c+b-2d}{b-c}\) with the assumption of \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\), we obtain that \( \alpha _{i}^\mathrm{L}\) must satisfy \(\alpha _{i}^\mathrm{L}\ge \frac{a+c-2d}{b-c}\). This result is, however, incompatible with condition \(\alpha _{i}^\mathrm{H}<\frac{a+c-2d }{b-c}\) that we obtained for the concerned player \(i\) since, by definition, envy concerns must satisfy \(\alpha _{i}^\mathrm{H}>\alpha _{i}^\mathrm{L}\).) As a consequence, this separating strategy profile cannot be sustained as a PBE of the game.
Let us now analyze the opposite separating strategy profile in which the highly concerned player \(i\) defects but the unconcerned player \(i\) cooperates. First, note that after observing an action from player \(i\) in the first-period stage game, player \(j\)’s beliefs in this separating strategy profile are updated to \(\mu (\beta _{i}^\mathrm{H}|C)=0\) and \(\mu (\beta _{i}^\mathrm{H}|D)=1\). Given these beliefs, let us now analyze player \(j\)’s best response during the second period game. In particular, after observing C in the first-period stage game, he believes that his opponent is unconcerned about fairness, thus implying that his opponent will not cooperate in the second-period game. Player \(j\) defects as a consequence in the second-period PD game since \(d>c-\alpha _{j}(b-c)\). By contrast, after observing D in the first period, player \(j\) believes that his opponent is highly concerned, and therefore that his opponent will cooperate in the second-period stage game. It follows that player \(j\) cooperates in the second period since \(a\ge b-\beta _{j}(b-c)\) given that \(\beta _{j}\ge \frac{b-a}{b-c}\) by definition. Let us now examine the first-period game. Regarding the uninformed player \(j\), he must choose C or D according to an expected utility calculation. In particular, player \(j\) cooperates during the first-period PD game if and only if
That is, if \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\). Let us now investigate the informed player \(i\)’s actions during the first-period stage game:
-
1.
If \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\), the uninformed player \(j\) cooperates during the first-period stage game. On the one hand, the highly concerned player \(i\) defects (as prescribed) if \(a+d\le b-\beta _{i}^\mathrm{H}(b-c)+a\), or \(\beta _{i}^\mathrm{H}\le \frac{b-d}{b-c}\), where \(\frac{b-d}{ b-c}>\frac{b-a}{b-c}\), and hence player \(i\) defects when being highly concerned if \(\frac{b-a}{b-c}\le \beta _{i}^\mathrm{H}\le \frac{b-d}{b-c}\). On the other hand, the unconcerned player \(i\) cooperates (as prescribed) if \( a+d\ge b-\beta _{i}^\mathrm{L}(b-c)+b-\beta _{i}^\mathrm{L}(b-c)\), which implies that \( \beta _{i}^\mathrm{L}\ge \frac{2b-a-d}{2(b-c)}\), which cannot hold since \(\frac{ 2b-a-d}{2(b-c)}>\frac{b-a}{b-c}\) and \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\). Hence, this separating strategy profile cannot be sustained if \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\).
-
2.
If \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\), the uninformed player \(j\) defects during the first-period stage game. On the one hand, the highly concerned player \(i\) cooperates if \(c-\alpha _{i}^\mathrm{H}(b-c)+d\le d+a\) , or \(\frac{c-a}{b-c}<0\le \alpha _{i}^\mathrm{H}\), which is true by definition. On the other hand, the unconcerned player \(i\) defects since \(c-\alpha _{i}^\mathrm{L}(b-c)+d\le d+b-\beta _{i}^\mathrm{L}(b-c)\), or \((b-c)(\beta _{i}^\mathrm{L}-\alpha _{i}^\mathrm{L})\ge (b-c)\), which can only hold if \(\beta _{i}^\mathrm{L}\ge \alpha _{i}^\mathrm{L}\), which is false by definition. Hence, this separating strategy profile cannot be supported if \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\).
Pooling equilibrium. Let us analyze the pooling strategy profile where both types of informed player \(i\) cooperate in the first period of the game. First, note that after observing an action from player \(i\) in the first-period stage game, player \(j\)’s beliefs in this pooling strategy profile are \(\mu (\beta _{i}^\mathrm{H}|C)=q\) (in equilibrium) and \(\mu (\beta _{i}^\mathrm{H}|D)\equiv \gamma \in [0,1]\) (off-the-equilibrium path). Given these beliefs, let us now analyze player \(j\)’s best response during the second period of the game. In particular, after observing C in the first period (in equilibrium) player \(j\) cannot infer player \(i\)’s social preferences and must therefore select C or D in the second period according to an expected utility comparison. In particular, player \(j\) cooperates in the second-period PD game if and only if
That is, if \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\). Similarly, in the first-period stage game, player \(j\) is uninformed about player \(i\)’s concern for fairness, and hence chooses to cooperate in the first-period PD game according to the same cutoff strategy on the prior probability that player \( i \)’s type is high. After observing that player \(i\) selected D in the first-period stage game (off-the-equilibrium) player \(j\) cannot infer player \(i\)’s social preferences either, and must therefore select C or D in the second period of the game according to an expected utility comparison. Specifically, player \(j\) cooperates in the second period if and only if
That is, if \(\gamma \ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\). Let us now investigate the informed player \(i\)’s actions during the first-period stage game:
-
1.
If \(q,\gamma \ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\) player \(j\) cooperates in both the first and second periods of the game, both after observing that player \(i\) selects C and D. On the one hand, the highly concerned player \(i\) cooperates if \(a+a\ge b-\beta _{i}^\mathrm{H}(b-c)+a\), which holds since \(\beta _{i}^\mathrm{H}\ge \frac{b-a}{b-c}\) by definition. On the other hand, the unconcerned player \(i\) defects since \(a+b-\beta _{i}^\mathrm{L}(b-c)\le b-\beta _{i}^\mathrm{L}(b-c)+b-\beta _{i}^\mathrm{L}(b-c)\), which holds given that \(\beta _{i}^\mathrm{L}<\frac{b-a}{b-c}\). Therefore, this pooling strategy profile cannot be supported if \(q,\gamma \ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})\).
-
2.
If \(q,\gamma <q^\mathrm{Sim}(\alpha _{j},\beta _{j})\) player \(j\) defects both in the first and second periods of the game, both after observing that player \(i\) selects C and D. The highly concerned player \(i\) defects, however, since \(c-\alpha _{i}^\mathrm{H}(b-c)+d\le d+d\), which implies \(\alpha _{i}^\mathrm{H}\ge 0\ge \frac{c-d}{b-c}\), which holds by definition. Hence, this pooling strategy profile cannot be sustained if \(q,\gamma <q^\mathrm{Sim}(\alpha _{j},\beta _{j})\).
-
3.
If \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})>\gamma \) player \(j\) cooperates in the first period of the game and in the second period he cooperates only after observing that player \(i\) chose C in the first-period stage game. On the one hand, the highly concerned player \(i\) cooperates since \(a+a\ge b-\beta _{i}^\mathrm{H}(b-c)+d\), or \(\beta _{i}^\mathrm{H}\ge \frac{b+d-2a }{b-c}\). Given that \(\frac{b-a}{b-c}>\frac{b+d-2a}{b-c}\), then condition \( \beta _{i}^\mathrm{H}\ge \frac{b+d-2a}{b-c}\) is satisfied from \(\beta _{i}^\mathrm{H}\ge \frac{b-a}{b-c}\). On the other hand, the unconcerned player \(i\) cooperates since \(a+b-\beta _{i}^\mathrm{L}(b-c)\ge b-\beta _{i}^\mathrm{L}(b-c)+d\), or \(a\ge d\). Hence, this pooling strategy profile can be supported as a PBE for \(q\ge q^\mathrm{Sim}(\alpha _{j},\beta _{j})>\gamma \).
-
4.
If \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\le \gamma \) player \(j\) defects in the first period of the game and in the second period he defects only after observing that player \(i\) selected C in the first-period stage game. The highly concerned player \(i\) defects, however, since \(c-\alpha _{i}^\mathrm{H}(b-c)+a\le d+a\), which implies \(\alpha _{i}^\mathrm{H}\ge 0\ge \frac{c-d }{b-c}\), which is satisfied by definition. Thus, this pooling strategy profile cannot be sustained if \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\le \gamma \). \(\square \)
1.3 Proof of Corollary 1
Informed player \(i\). Under complete information, when player \(i\) is highly concerned, i.e., when \(\beta _{i}\ge \frac{b-a}{b-c}\), then players’ preferences satisfy \(\beta _{i},\beta _{j}\ge \frac{b-a}{b-c}\), implying that outcome (C,C) can be sustained in pure strategies under complete information. (As discussed in Sect. 5.1, we assume that, for simplicity, players can resort to some kind of coordination mechanism, such as social norms or a common randomization device by which players are able to coordinate on the efficient, cooperative outcome (C,C). Thus, if this simultaneous-move game is repeated twice, (C,C) would arise during both periods when both players’ guilt aversion is sufficiently high.) In this context, player \(j\)’s equilibrium utility is \(a+a\). When player \(i\) is privately informed about his high concern for fairness, \(\beta _{i}\ge \frac{b-a}{b-c}\), then outcome (C,C) is similarly played during both stages of the repeated game, thus yielding the same equilibrium utility for player \( i\). If, by contrast, player \(i\) has low concerns for fairness, i.e., \(\beta _{i}<\frac{b-a}{b-c}\), then players’ preferences satisfy \(\beta _{j}\ge \frac{b-a}{b-c}>\beta _{i}\), implying that outcome (D,D) can be supported under complete information. Hence, if this simultaneous-move game is repeated twice, (D,D) would arise during both periods when at least one player’s guilt aversion is sufficiently high. Player \(i\)’s equilibrium utility is thus \(d+d\). When player \(i\) is privately informed about his low concern for fairness, \(\beta _{i}<\frac{b-a}{b-c}\), then Proposition 1 shows that outcome (C,C) can be sustained in the first-period stage game, while (D,C) emerges in the second-period stage game, thus entailing an equilibrium utility of \(a+b-\beta _{i}(b-c)\) for player \(i\). Therefore, player \(i\)’s equilibrium utility under incomplete information \(a+b-\beta _{i}(b-c)\), is larger than that under complete information, \(d+d\), if \(\beta _{i}\le \frac{ a+b-2d}{b-c}\). Note that this condition holds for all \(\beta _{i}<\frac{b-a}{ b-c}\), given that \(\frac{b-a}{b-c}<\frac{a+b-2d}{b-c}\), which is satisfied since \(a>d\) by assumption. Therefore, player \(i\)’s equilibrium utility is weakly larger under incomplete than complete information for all parameter values.
Uninformed player \(j\). Let us investigate whether player \( j \) obtains a larger expected utility in the complete or incomplete information version of the game. In particular, if we first evaluate player \( j\)’s expected utility in the complete information game, but before being informed about which is player \(i\)’s type (concerned or unconcerned), we obtain \(q[a+a]+(1-q)[d+d]\). Specifically, the first component denotes the case in which player \(j\) is informed about player \(i\) being concerned for fairness, which yields the (C,C) outcome in both periods. The second component, however, reflects the case in which player \(j\) is informed about player \(i\) being unconcerned, whereby only the (D,D) outcome can be sustained under complete information; as shown in Sect. 3. By contrast, in the incomplete information game, the uninformed player \(j\)’s expected utility is \(q[a+a]+(1-q)[a+c-\alpha _{j}(b-c)]\), where the first component represents the payoffs he obtains when player \(i\)’s type is high and (C,C) is played in both periods, while the second component describes his utility when player \(i\)’s type is low, whereby (C,C) arises in the first period of interaction, but (D,C) emerges in the second period. Hence, player \(j\)’s ex-ante expected utility is larger in the incomplete than the complete information version of the game if and only if
which simplifies to \(a+c-\alpha _{j}(b-c)>2d\), or \(\alpha _{j}\le \frac{ a+c-2d}{b-c}\). Note that this condition on \(\alpha _{j}\) is compatible with the initial assumption of \(\alpha _{j}\ge \beta _{j}\ge \frac{b-a}{b-c}\) if \(\frac{b-a}{b-c}<\frac{a+c-2d}{b-c}\), i.e., if \(2a-b>2d-c\), which holds when the payoff from promoting the cooperative outcome (C,C) is sufficiently high. \(\ \square \)
1.4 Proof of Proposition 2
Separating PBE. Let us first analyze the separating strategy profile where the (privately informed) second mover cooperates when being concerned about fairness but defects otherwise. First, note that after observing an action from the second mover in the first-period sequential-move game, the first mover’s beliefs about \(\beta _{2}^\mathrm{H}\) are updated according to Bayes’ rule and become \(\mu (\beta _{2}^\mathrm{H}|C)=1\) and \( \mu (\beta _{2}^\mathrm{H}|D)=0\). Given these beliefs, the first mover cooperates in the second period after observing that the second mover cooperated in the first-period stage game, but defects otherwise. After these choices, the second mover reciprocates the first mover in the second-period stage game if the second mover’s concerns are high, but defects otherwise.
During the first-period stage game, the second mover cooperates when being concerned but defects otherwise, as prescribed. Hence, the uninformed first mover cooperates if the expected utility from cooperation exceeds that from defection. That is,
or \(q\ge q^\mathrm{Seq}(\alpha _{1})\). Let us finally investigate the second mover’s behavior during the first-period game:
-
1.
If \(q\ge q^\mathrm{Seq}(\alpha _{1})\), the first mover cooperates in the first-period stage game. On the one hand, the concerned second mover cooperates if \(a+a\ge b-\beta _{2}^\mathrm{H}(b-c)+d\), since defection is responded with defection in the subsequent stage game. Solving for \(\beta _{2}^\mathrm{H}\), we obtain that the highly concerned second mover cooperates (as prescribed) if \( \beta _{2}^\mathrm{H}\ge \frac{b-d-2a}{b-c}\). In addition, since \(\frac{b-a}{b-c}> \frac{b-d-2a}{b-c}\) and \(\beta _{2}^\mathrm{H}\ge \frac{b-a}{b-c}\) by definition, condition \(\beta _{2}^\mathrm{H}\ge \frac{b-d-2a}{b-c}\) holds. Therefore, the concerned second mover cooperates in the first period, as prescribed in this separating strategy profile. On the other hand, the unconcerned second mover defects if \(a+[b-\beta _{2}^\mathrm{L}(b-c)]<[b-\beta _{2}^\mathrm{L}(b-c)]+d\), i.e., \(a<d\), which violates our initial assumptions. Hence, the unconcerned second mover also cooperates in the first period, implying that this separating strategy profile cannot be sustained as a PBE if priors satisfy \(q\ge q^\mathrm{Seq}(\alpha _{1})\).
-
2.
If \(q<q^\mathrm{Seq}(\alpha _{1})\), the first mover defects in the first-period stage game. On the one hand, the concerned second mover cooperates if \(c-\alpha _{2}^\mathrm{H}(b-c)+a\ge d+d\), or \(\alpha _{2}^\mathrm{H}\le \frac{a+c-2d}{ b-c}\). On the other hand, the unconcerned second mover defects if \(c-\alpha _{2}^\mathrm{L}(b-c)+b-\beta _{2}^\mathrm{L}(b-c)\le d+d\), which implies \(\frac{c+b-2d}{ b-c}\le \alpha _{2}^\mathrm{L}+\beta _{2}^\mathrm{L}\). Thus, for a separating equilibrium to exist, in which the second mover cooperates only when he is concerned about fairness, the first mover’s beliefs must satisfy \(q<q^\mathrm{Seq}(\alpha _{1})\) and parameter values must satisfy \(\alpha _{2}^\mathrm{H}\le \frac{a+c-2d}{ b-c}\) and \(\frac{c+b-2d}{b-c}\le \alpha _{2}^\mathrm{L}+\beta _{2}^\mathrm{L}\). The initial condition \(\beta _{2}^\mathrm{L}<\frac{b-a}{b-c}\) and \(\alpha _{2}^\mathrm{L}+\beta _{2}^\mathrm{L}\ge \frac{c+b-2d}{b-c}\), however, are incompatible with \(\alpha _{2}^\mathrm{H}\le \frac{a+c-2d}{b-c}\). [See the discussion in the proof of Proposition 1, specifically when checking for the existence of a separating equilibrium in the case that priors satisfy \(q<q^\mathrm{Sim}(\alpha _{j},\beta _{j})\).] As a consequence, this separating strategy profile cannot be sustained as a PBE of the game.
Pooling PBE. Let us now analyze the pooling strategy profile where both types of second mover cooperate in the first-period stage game. First, note that after observing an action from the second mover during the first-period sequential-move PD game, the first mover’s beliefs about \( \beta _{2}^\mathrm{H}\) in this pooling strategy profile cannot updated using Bayes’ rule and hence are \(\mu (\beta _{2}^\mathrm{H}|C)=q\) (in equilibrium) and \(\mu (\beta _{2}^\mathrm{H}|D)\equiv \gamma \in [0,1]\) (off-the-equilibrium path). Given these beliefs, the first mover cooperates in the second-period stage game after observing that the second mover chose C (in equilibrium) in the first-period stage game if \(q\ge q^\mathrm{Seq}(\alpha _{1})\). If the first mover observes the second mover selecting D in the first-period stage game (off-the-equilibrium path), then he cooperates in the second-period stage game if and only if
That is, if \(\gamma \ge q^\mathrm{Seq}(\alpha _{1})\). Let us now investigate the informed player (the second mover) during the first-period sequential-move game:
-
1.
If \(q,\gamma \ge q^\mathrm{Seq}(\alpha _{1})\) the first mover cooperates in both the first- and second-period stage game after observing any action from the second mover in the first-period stage game. On the one hand, the concerned second mover cooperates (as prescribed) if \(a+a\ge b-\beta _{2}^\mathrm{H}(b-c)+a\), which holds since \(\beta _{2}^\mathrm{H}\ge \frac{b-a}{b-c}\) by definition. On the other hand, the unconcerned second mover defects since \( a+b-\beta _{2}^\mathrm{L}(b-c)\le b-\beta _{2}^\mathrm{L}(b-c)+b-\beta _{2}^\mathrm{L}(b-c)\), which holds since \(\beta _{2}^\mathrm{L}<\frac{b-a}{b-c}\) by definition. Therefore, this pooling strategy profile cannot be supported as a PBE if \(q,\gamma \ge q^\mathrm{Seq}(\alpha _{1})\).
-
2.
If \(q,\gamma <q^\mathrm{Seq}(\alpha _{1})\) the first mover defects both in the first- and second-period stage game, both after observing that the second mover selects C and D in the first-period stage game. The concerned second mover defects, however, since \(c-\alpha _{2}^\mathrm{H}(b-c)+d\le d+d\), which implies \(\alpha _{2}^\mathrm{H}\ge 0\ge \frac{c-d}{b-c}\), which holds by definition. Hence, this pooling strategy profile cannot be sustained as a PBE if \(q,\gamma <q^\mathrm{Seq}(\alpha _{1})\).
-
3.
If \(q\ge q^\mathrm{Seq}(\alpha _{1})>\gamma \) the first mover cooperates in the first-period stage game, while in the second-period stage game he cooperates only after observing that the second mover selected C (in equilibrium) in the first-period stage game. On the one hand, the concerned second mover cooperates since \(a+a\ge b-\beta _{2}^\mathrm{H}(b-c)+d\), or \(\beta _{2}^\mathrm{H}\ge \frac{b+d-2a}{b-c}\). Given that \(\frac{b-a}{b-c}>\frac{b+d-2a}{ b-c}\), then condition \(\beta _{2}^\mathrm{H}\ge \frac{b+d-2a}{b-c}\) is satisfied from \(\beta _{2}^\mathrm{H}\ge \frac{b-a}{b-c}\). On the other hand, the unconcerned second mover cooperates since \(a+b-\beta _{2}^\mathrm{L}(b-c)\ge b-\beta _{2}^\mathrm{L}(b-c)+d\), or \(a\ge d\). Hence, this pooling strategy profile can be supported as a PBE for \(q\ge q^\mathrm{Seq}(\alpha _{1})>\gamma \).
-
4.
If \(q<q^\mathrm{Seq}(\alpha _{1})\le \gamma \) the first mover defects in the first-period stage game, while in the second-period stage game he defects only after observing that the second mover chose C (in equilibrium) in the first-period stage game. The concerned second mover defects, however, since \( c-\alpha _{2}^\mathrm{H}(b-c)+d\le d+a\), which implies \(\alpha _{2}^\mathrm{H}\ge 0\ge \frac{c-a}{b-c}\), which is satisfied by definition. Thus, this pooling strategy profile cannot be sustained as a PBE if \(q<q^\mathrm{Seq}(\alpha _{1})\le \gamma \). \(\square \)
1.5 Proof of Corollary 2
Second mover. When he is highly concerned about fairness, i.e., when \(\beta _{2}\ge \frac{b-a}{b-c}\), then players’ preferences satisfy \( \beta _{1},\beta _{2}\ge \frac{b-a}{b-c}\), implying that outcome (C,C) can be sustained in pure strategies under complete information. (Thus, if this sequential-move game is repeated twice, (C,C) would arise during both periods when both players’ guilt aversion is sufficiently high.) In this context, the second mover’s equilibrium utility is \(a+a\) under complete information. When the second mover is privately informed about his own high concern for fairness, \(\beta _{2}\ge \frac{b-a}{b-c}\), then outcome (C,C) is similarly played during both stages of the repeated game (as described in Proposition 2), thus yielding the same equilibrium utility for the (informed) first mover. When, instead, the first mover is informed that his concern for fairness is low, i.e., \(\beta _{2}<\frac{b-a}{b-c}\), players’ preferences satisfy \(\beta _{1}\ge \frac{b-a}{b-c}>\beta _{2}\), implying that the outcome (D,D) can be supported under complete information, as described in Lemma 1. Hence, if this sequential-move game is repeated twice, (D,D) would arise during both periods, entailing that an equilibrium utility of \(d+d\) for the second mover. When the second mover is privately informed about his low concern for fairness, \(\beta _{2}<\frac{b-a}{b-c}\), then Proposition 2 shows that in the first-period sequential-move game both players cooperate, while in the second-period game the first mover cooperates and the second mover responds by defecting. Therefore, the second mover’s equilibrium utility under incomplete information, \(a+b-\beta _{2}(b-c)\), is larger than that under complete information, \(d+d\), if \(\beta _{2}\le \frac{a+b-2d}{b-c}\). Note that this condition holds for all \(\beta _{2}<\frac{b-a}{b-c}\), given that \(\frac{b-a}{b-c}<\frac{a+b-2d}{b-c}\), which is satisfied since \(a>d\) by assumption. Therefore, the second mover’s equilibrium utility is weakly larger under incomplete than under complete information for all parameter values.
First mover. Let us investigate whether the uninformed first mover obtains a larger expected utility in the complete or incomplete information game. First, under complete information, the first mover obtains an expected utility of \(q[a+a]+(1-q)[d+d]\). The first component reflects the fact that the first mover is informed about the second mover’s concerns being high and, since his own concerns are also high, outcome (C,C) can be supported in both periods; as shown in Lemma 1. However, the second component represents the case in which the first mover is informed that the second mover is unconcerned. In this case, the first mover can anticipate that any of his actions will be responded to with defection and, as shown in Lemma 1, the only outcome that can be sustained in equilibrium is (D,D) during both periods of interaction. In contrast, when players compete in the incomplete information game, the expected utility of the uninformed first mover is \( q[a+a]+(1-q)[a+c-\alpha _{1}(b-c)]\). Indeed, the first component corresponds to the case where the second mover has high fairness concerns, which implies the cooperative outcome (C,C) obtains in both time periods, while the second component corresponds to the case where the second mover’s fairness concerns are low. In that setting, as described in the backstabbing equilibrium identified of Proposition 2, both players cooperate in their first period of interaction, but in the second period the (uninformed) first mover cooperates while the (informed) second mover responds by defecting. Comparing the first mover’s expected utility in both settings, we obtain that he prefers to remain uninformed if
which reduces to \(a+c-\alpha _{1}(b-c)-2d>0\), or \(\alpha _{1}\le \frac{ a+c-2d}{b-c}\). Note that this condition on \(\alpha _{1}\) is compatible with the initial assumption of \(\alpha _{1}\ge \beta _{1}\ge \frac{b-a}{b-c}\) if \(\frac{b-a}{b-c}<\frac{a+c-2d}{b-c}\), i.e., if \(2a-b>2d-c\), which holds when the payoff from promoting the cooperative outcome (C,C) is sufficiently high.\(\square \)
1.6 Proof of Corollary 3
Separating PBE. Let us first analyze the separating strategy profile where the first mover cooperates when he has high concerns for fairness but defects otherwise. First, note that after observing an action from the first mover in the first-period sequential-move PD game, the second mover’s beliefs about \(\beta _{1}^\mathrm{H}\) are updated according to Bayes’ rule, becoming \(\mu (\beta _{1}^\mathrm{H}|C)=1\) and \(\mu (\beta _{1}^\mathrm{H}|D)=0\). Recall that the second mover is concerned about fairness by definition, \(\beta _{2}^\mathrm{H}\ge \frac{b-a}{b-c}\), and that this information is common knowledge. Hence, given the above beliefs, the second mover’s best response is to “mimic” the action selected by the first mover (as described in Lemma 1), both in the first and second-period sequential PD games. Regarding the first mover, when he has high concerns for fairness he cooperates since \(a+a\ge d+d\). If unconcerned, the first mover defects (as prescribed) if \(a+d<d+d\), which cannot hold given that \(a>d\) by definition. Hence, the separating strategy profile cannot be supported as a PBE of the game.
Pooling PBE. Let us now analyze the pooling strategy profile where both types of first mover cooperate in the first-period game. First, note that after observing an action from the first mover during the first-period sequential-move PD game, the second mover’s beliefs about \(\beta _{1}^\mathrm{H}\) become \(\mu (\beta _{1}^\mathrm{H}|C)=q\) (in equilibrium) and \(\mu (\beta _{1}^\mathrm{H}|D)\equiv \gamma \in [0,1]\) (off-the-equilibrium path). Because the second mover’s best response is to “mimic” the action selected by the first mover, we do not need to analyze equilibrium played under different beliefs as we did in the proof of Proposition 2. Regarding the first mover, when he has high concerns for fairness he cooperates since \(a+a\ge d+d\). If unconcerned, the first mover also cooperates (as prescribed) given that \(a+a\ge d+d\). Hence, the pooling strategy profile can be supported as a PBE of the game, for all \(q\) and \(\gamma \in [0,1]\). \(\square \)
Rights and permissions
About this article
Cite this article
Duffy, J., Muñoz-García, F. Cooperation and signaling with uncertain social preferences. Theory Decis 78, 45–75 (2015). https://doi.org/10.1007/s11238-013-9400-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11238-013-9400-5
Keywords
- Prisoner’s dilemma
- Social preferences
- Inequity aversion
- Incomplete information
- Signaling
- Information transmission