The dynamical renaissance in neuroscience

Abstract

Although there is a substantial philosophical literature on dynamical systems theory in the cognitive sciences, the same is not the case for neuroscience. This paper attempts to motivate increased discussion via a set of overlapping issues. The first aim is primarily historical and is to demonstrate that dynamical systems theory is currently experiencing a renaissance in neuroscience. Although dynamical concepts and methods are becoming increasingly popular in contemporary neuroscience, the general approach should not be viewed as something entirely new to neuroscience. Instead, it is more appropriate to view the current developments as making central again approaches that facilitated some of neuroscience’s most significant early achievements, namely, the Hodgkin–Huxley and FitzHugh–Nagumo models. The second aim is primarily critical and defends a version of the “dynamical hypothesis” in neuroscience. Whereas the original version centered on defending a noncomputational and nonrepresentational account of cognition, the version I have in mind is broader and includes both cognition and the neural systems that realize it as well. In view of that, I discuss research on motor control as a paradigmatic example demonstrating that the concepts and methods of dynamical systems theory are increasingly and successfully being applied to neural systems in contemporary neuroscience. More significantly, such applications are motivating a stronger metaphysical claim, that is, understanding neural systems as being dynamical systems, which includes not requiring appeal to representations to explain or understand those phenomena. Taken together, the historical claim and the critical claim demonstrate that the dynamical hypothesis is undergoing a renaissance in contemporary neuroscience.

1 Introduction

Throughout the mid-twentieth century, many areas of psychology underwent a “cognitive revolution” (Bechtel and Graham 1999; Thagard 2005). This revolution drove an information-processing perspective of mind (Stillings et al. 1995), namely, mental activity like decision-making and problem solving, as well as goal-directed behavior. This perspective centered on explaining mind in terms of representations that encoded and decoded information and the computational procedures that acted on them (Thagard 2019; Von Eckardt 1995). During that time, the neurosciences were primarily concerned with behavior and physiology (Cooper and Shallice 2010). Accordingly, conceptual tools gaining traction in cognitive science (e.g., computation and representation) were largely not employed. On the other hand, throughout the 1980s and 1990s, research in cognitive science centered more on neurobiologically-inspired accounts of cognition, especially artificial neural networks like connectionism (Cooper and Shallice 2010; Rumelhart 1989). Even though neurobiologically-inspired concepts and models gained prominence, the information-processing perspective remained and cognition was defined in terms of computations and representations (Boden 2006). The widespread application of such information-processing conceptions of mind presumably left many in agreement with Fodor (1975) in thinking that computational and representational approaches were “the only game in town” (Rescorla 2020).

This overview is, of course, quite simplistic and leaves out significant facts. For example, various mind sciences—broadly construed—were not impacted by the cognitive revolution and its information-processing perspective. Ecological psychology (Gibson 1979/1986), embodiment (Varela et al. 1991), and synergetics (Haken et al. 1985), to name a few, carried out rich research programs without appeal to concepts such as “computation” or “representation” in their accounts of mental activity or goal-directed behavior. Many of these research programs did not just adhere to different concepts, methods, and theories, but were also staunchly opposed to understanding the mind in computational or representational terms. Yet, proponents of information-processing accounts were left asking, “If mind is not computational or representational, then what is it?” Throughout the 1990s, van Gelder (1995) and others published a number of works answering just that question: Mind is best understood not in computational or representational terms, but in terms of dynamical systems theory. The claim that mind is fundamentally dynamic in nature captured what was at the heart of a variety of noninformation-processing accounts of mind. The concepts and methods of dynamical systems theory are regularly central to research by ecological psychologists (Chemero 2009), proponents of embodiment and enactivism (Thompson 2007), and work in coordination dynamics and synergetics (Kelso 2009). What about dynamical systems theory in neuroscience; does it provide a viable investigative framework? Answering that question is the primary purpose of this paper.

I have two aims here: The first aim is primarily historical and is to demonstrate that dynamical systems theory is currently experiencing a renaissance in neuroscience. Although dynamical concepts and methods are becoming increasingly popular in contemporary neuroscience, the general approach should not be viewed as something entirely new to neuroscience. Instead, it is more appropriate to view the current developments as making central again approaches that facilitated some of neuroscience’s most significant early achievements during the mid-twentieth century. The second aim is primarily critical and defends a version of the “dynamical hypothesis” in neuroscience. Whereas the original version centered on defending, among other things, nonrepresentational accounts of cognition, the version I have in mind is broader and includes the substrates of cognitive systems as well. In view of that, I discuss research on motor control as a paradigmatic example that demonstrates that the concepts and methods of dynamical systems theory are increasingly and successfully being applied to a wide range of neural systems in neuroscience. More significantly, such applications are motivating a stronger metaphysical claim, that is, understanding neural systems as being dynamical systems, which includes not requiring appeal to representations to explain or understand those phenomena.

In the next section, I focus on the first aim and describe the dynamical renaissance. There, I introduce dynamical systems theory and dimensionality reduction. I highlight the significant role the latter has come to play in dynamical accounts of neural phenomena, with an emphasis on two historical examples of its application: the Hodgkin–Huxley and FitzHugh–Nagumo models. In the section that follows, I focus on the second aim, and present representational and dynamical systems explanations of motor control in order to demonstrate how the dynamical renaissance is motivating a reexamination of the necessity of appealing to “representations” in explanations of neural phenomena.

2 The dynamical renaissance

A “renaissance” can be defined as “a situation when there is new interest in something and it becomes strong and active again” (Combley 2011). This term is an appropriate description of what is happening in neuroscience because although the concepts and methods of dynamical systems theory can be viewed as novel in many contemporary subdisciplines of neuroscience, the fact is that the general approach was employed in research on a number of the field’s foundational discoveries in the mid-twentieth century. The claim here is not that dynamical systems theory, broadly construed, has been absent from all neuroscience practice during those intervening years. It is clear that some dynamical tools—especially differential equations—have been standardly applied in neuroscience research for decades.¹ Much of this work employs dynamical tools in order to model the electrophysiological properties of neurons, particularly those concerning neuronal circuits and synaptic organization (Izhikevich 2007, pp. xv–xvi). Consequently, the dynamic properties of neural systems have not on their own been central topics of investigation. Thus, dynamical systems theory concepts such as “fixed point attractors,” “limit cycles,” and “phase transitions,” as well as particular methods for analyzing and describing those properties, have not been regularly employed. It is those features and methods that make dynamical systems theory uniquely qualified for investigating the dynamics—especially nonlinear dynamics—of biological systems like neurons and neuronal networks. Thus, historically speaking, when dynamical systems theory has been seen in neuroscience, it has commonly been in the service of investigating neurophysiology and organization.² Moreover, such research has been informed by information-processing views of neuronal activity and organization, including single neurons (e.g., Koch 1999) and populations of neurons (e.g., Schöner et al. 2016). Such claims draw attention to a number of controversial issues recognizable by those familiar with particular debates in the cognitive sciences and philosophy of mind.³ One debate concerns the fact that many proponents of dynamical systems theory in the cognitive sciences have not only supported use of its concepts and methods, but they have also championed a controversial position regarding the nature of cognition: the dynamical hypothesis.

In the cognitive sciences and philosophy of mind, the dynamical hypothesis centers on two claims (Port and van Gelder 1995; van Gelder 1998). First, is the knowledge hypothesis, which is an epistemological claim centering on the idea that cognitive agents can be understood as dynamical systems (Chemero 2000; van Gelder 2006). Taken in isolation, that idea need not be controversial because it merely advocates for the use of, for example, data analysis methods from dynamical systems theory (e.g., differential equations) to generate hypotheses, create models, and to quantify cognition and related phenomena (e.g., goal-directed behavior). However, it becomes more provocative when coupled with the second claim: the nature hypothesis, which is an ontological thesis centering on the idea that cognitive agents are dynamical systems. What makes this second claim controversial is that it eschews explaining cognition in terms of information processing, in particular, it rejects understanding cognition as essentially computational or representational. This makes the first claim more provocative because it has the consequence of removing the need to appeal to the stronger forms of “representations” invoked in cognitive science research (e.g., representations with semantic properties; Pitt 2020). Given that information-processing accounts are currently accepted by many to be the “thoroughly entrenched conception” of cognition and neural systems (Shapiro 2013, p. 362), such that it would be either “confusion or brazenness” (Shapiro 2013, pp. 362–363) to reject explaining mental activity and behavior in computational and representational terms (cf. Favela and Martin 2017), it is not surprising that the dynamical hypothesis draws many a skeptical eye from contemporary researchers. The goal of this section is not to defend or reject the dynamical hypothesis. In keeping with the thesis of this section, I merely aim to demonstrate that dynamical systems theory—both in terms of epistemology (i.e., methods) and metaphysics (i.e., the nature of cognitive systems)—is not as novel to neuroscience as one could believe based on the ways it is discussed in the literature.⁴ Instead, its increasing popularity is in fact a return to practices that were common in the history of neuroscience. As a historical point, that goal is achievable without taking a stand on the dynamical hypothesis’ metaphysical claim. Accordingly, as I assume readers are unfamiliar with it, a brief introduction to dynamical systems theory is provided in the following subsection. After, I provide historical examples of its application.

2.1 A very concise introduction to dynamical systems theory

There are many excellent general introductions to dynamical systems theory (e.g., Alligood et al. 2000; Fuchs 2013; Guckenheimer and Holmes 1983; Strogatz 2015), as well as its applications in the mind sciences (e.g., Beer 2000; Chemero 2009; Clark 1997; Guastello et al. 2011; Port 2006; Riley and Holden 2012; Thelen and Smith 1994). The current introduction is aimed at providing a general overview and giving a sense of the aspects of dynamical systems theory that will be most significant in later sections (Favela 2020). To begin, dynamical systems theory is a branch of mathematics that can evaluate both abstract and physical systems as they change over time. One way to understand how dynamical systems theory is applied is in terms of its quantitative and qualitative elements. The quantitative element is the application of mathematical equations to describe, evaluate, and measure systems. A common dynamical mathematical tool is differential equations, which are mathematical functions that capture systems’ temporal evolutions, where variables in the equations are continuous values, as opposed to discrete values. The qualitative element is the visual depiction of the dynamics by means of plotting the equations in a state space, which is the range of possible values of a variable as depicted by means of a phase space plot.⁵

It is likely that many philosophers with at least some familiarity with dynamical systems theory know it by way of van Gelder’s discussion of the Watt centrifugal governor example (van Gelder 1995). Because that example is best described by van Gelder himself, I refer readers to that primary source (for those interested in secondary sources, I recommend Chemero 2000 and Shapiro 2019). Moreover, that example has been the target of much debate (e.g., Eliasmith 1997), which I do not wish to detract from the current aim of providing a concise and uncontroversial account of dynamical systems theory. Accordingly, here I provide pendulum dynamics as a more straightforward example. The quantitative element of a dynamical systems account of pendulum dynamics is the following:

$$ \frac{{d^{2} \theta }}{{dt^{2} }} + \frac{g}{l}\sin \theta = 0 $$

(1)

In this differential equation, $0$ is the pendulum swing, which is the phenomenon of interest. Angular displacement of arm ($\theta$), gravitational acceleration ($g$), and pendulum length ($l$) are the identified variables contributing to and most responsible for the dynamics of the phenomenon of interest. The qualitative element is the phase space plot of the pendulum swinging (Fig. 1). It is important to keep in mind that a qualitative description of the full range of the system’s dynamics via a state space is not intended to provide the kind of information or understanding that a diagram does. In the current context, a diagram of pendulum dynamics (Fig. 1a) is intended to provide understanding of the dynamics in real space. Here, the movement of a pendulum across two-dimensional space. The state space of pendulum dynamics (Fig. 1b) is intended to provide understanding of the dynamics abstractly. Here, the y-axis illustrates the velocity of the pendulum over time and the x-axis illustrates the angle of the pendulum at a time. For example, looking at (0, 0) on the phase space plot (Fig. 1b), tells you that the pendulum is around the resting position, and (− 2π, 0) and (2π, 0) illustrates the same motion but at opposite valued arm angles. Hence, the diagram provides an understanding of movement in actual physical space and the state space provides abstract understanding of the temporal space. Thus, taken together, the quantitative (e.g., differential equation) and qualitative (i.e., state space plot) elements are intended to provide explanations (e.g., contributions of variables) and understanding (i.e., abstract nature of the dynamics over time) of the phenomenon of interest.

Fig. 1

Depictions of pendulum dynamics. a Diagram of pendulum dynamics. The diagram is intended to provide understanding of the dynamics in real space. Here, the movement of a pendulum across two-dimensional space. b Phase space plot of pendulum dynamics. The state space is intended to provide understanding of the dynamics abstractly. Here, the y-axis illustrates the velocity of the pendulum over time ($\frac{d\theta }{dt}$) and the x-axis illustrates the pendulum arm’s angle at a time. Whereas the diagram (A) provides understanding of the actual physical space, the state space (B) provides abstract understanding of the temporal space. (Modified and reprinted with permission from Krishnavedala (2012). CC0 1.0 and Krishnavedala (2014). CC BY-SA 4.0.)

2.1.1 Dimensionality reduction

A more advanced topic than typically discussed in introductions to dynamical systems theory (especially in terms of the mind sciences), but one that will be crucial in later sections, is the intersection of dynamical systems theory and dimensionality reduction. In statistics and other forms of data analysis (e.g., machine learning), dimensionality (or dimensions) refers to the informative features of a dataset. For example, medical data such as blood pressure, temperature, white blood cell count, etc., are all features—or inputs—of a dataset obtained for the purpose of diagnosing an illness—or output. High-dimensional data refers to datasets with a “high” number (a relative amount) of features such that determining their relationships to each other and the phenomenon of interest can be computationally exceedingly demanding. For example, datasets comprised of gene expression are paradigmatic cases of high-dimensional data as there are seemingly innumerable relationships among genes, different temporal scales, etc. Dimensionality reduction, in the simplest terms, is a data processing strategy that attempts to cut down on the number of a dataset’s features without losing valuable information (Hinton and Salakhutdinov 2006; Nguyen and Holmes 2019; Sorzano et al. 2014). This is typically done in two general ways: filtering variables from the original dataset to keep only what is most relevant or exploiting redundancy in input data to find fewer new variables that contain the same information (Cohen 2017; Sorzano et al. 2014). As with any data processing or analysis techniques, one must be aware of the limitations of dimensionality reduction (Carlson et al. 2018; Jonas and Kording 2017). Yet, there are many virtues to employing dimensionality reduction on high-dimensional datasets, including its ability to: filter out meaningless noise (Cohen 2017), help control for incorrect intuitions about relationships among variables (Holmes and Huber 2018), increase a dataset’s statistical power (Nguyen and Holmes 2019), and reveal deeper organizational relationships and structures (Batista 2014).

Dimensionality reduction is not exclusive to dynamical systems theory. But for the aims of this paper, the most important way dimensionality reduction intersects with dynamical systems theory is for the purpose of reducing the number of variables needed to account for even the most complex of data from behavioral and cognitive tasks, as well as the underlying neural processes. With simple—usually human-made—systems, it can be relatively straightforward to identify the most relevant variables to account for the phenomenon of interest. As discussed above, the full range of pendulum dynamics can be understood via three variables: angular arm displacement ($\theta$), gravitational acceleration ($g$), and pendulum length ($l$). When it comes to neural systems and their related behaviors, however, variable identification is typically nowhere near as straightforward (Churchland and Abbott 2016; Churchland et al. 2012; Cunningham and Byron 2014; Frégnac 2017; Williamson et al. 2019). Since it is crucial to identify the relevant dimensions (i.e., features, variables) when developing models and equations of dynamical systems, various dimensionality reduction analyses can be employed. These methods include, but are not limited to, linear methods such as correspondence analysis and nonlinear methods such as diffusion maps (Nguyen and Holmes 2019). A popular method of dimensionality reduction in the mind sciences, and one that will come up in later section, is principal component analysis.

Here, I provide a brief and conceptually-focused introduction to principal component analysis (PCA; see Jolliffe and Cadima 2016 for a more technical introduction). While PCA has been around since the early-1900s, it was not until much more recently that the computational resources were available to leverage its techniques on high-dimensional datasets. The basic idea underlying PCA is to reduce a dataset’s dimensionality while preserving variability. Here, preserving variability means discovering new variables—principal components (PC)—with linear functions that match those in the original input data. Moreover, those new variables should maximize variance and be uncorrelated with each other (Jolliffe and Cadima 2016). Werner and colleagues provide fish body measurements as an illustrative and simple example of PCA (Werner et al. 2014). In this example, the input dataset contains height and length measurements of various fish (Fig. 2a). As it is assumed those two dimensions are strongly correlated, the PCA defines a change of coordinate systems from the original two-dimensional (height, length) data space to a single dimension (first shape score) data space (Fig. 2b). This reduction from two dimensions to one dimension retains the maximum amount of the original dataset’s variability.

Fig. 2

Principal component analysis (PCA) example. a Fish body measurements provide the input dataset, with height and length obtained from N individuals. b Height and length are assumed to be strongly correlated. PCA defines a change of coordinate system from the original (height, length)-axes (here, the x- and y-axes) to a new axes (B₁ and B₂), which depict the principle axes of the dimensions that covary. The process of defining a new coordinate system (V) corresponds to a reduction of the dimensionality of the data space, which also retains most of the data’s variability. (Modified and reprinted with permission from Werner et al. (2014). CC BY 4.0.)

As in the example of fish measurements (Fig. 2), when the various dimensionality reduction methods intersect with dynamical systems approaches, it is usually for the purpose of helping investigators get an epistemological grip on unwieldy data by contributing to the identification of the most relevant variables among multivariate datasets. Although dimensionality reduction in its contemporary form (e.g., via neural networks and other kinds of machine learning) is relatively new (~ early-2000s), issues concerning how to cope with high-dimensional data have been explicitly discussed in computer science (e.g., the “curse of dimensionality;” Bellman 1961) and statistics (Finney 1977) since the mid-1900s. It was around that time (give a decade back or two) that both dynamical systems approaches and forms of dimensionality reduction were contributing to some of the most significant research in neuroscience, namely, the Hodgkin–Huxley and FitzHugh–Nagumo models. In the following section, I present these cases to motivate the claim that contemporary applications of dynamical systems theory in neuroscience is not as much pioneering as it is a revival.

2.2 Dynamical systems theory in neuroscience, then and now

As mentioned above, it is common to view dynamical systems theory as merely an alternative or supplement to the information-processing approaches purported to be dominant in the contemporary mind sciences (e.g., Eliasmith 1996; Kaplan and Bechtel 2011). In this section, I present two historical cases to motivate both the claim that dynamical approaches were common in neuroscience research in the mid-1900s and that dimensionality reduction was part of practices that facilitated some of the field’s most lauded successes. I begin with Hodgkin and Huxley’s (1952) canonical model of action potentials. This Nobel Prize-earning work has been described as “elegant,” “groundbreaking,” and the most successful quantitative model in neuroscience (Gerstner et al. 2014; Koch 1999). A major feature of this work was the identification of the action potential (i.e., neuron spike) as a dynamic (i.e., temporal) event defined by relatively few variables (i.e., dimensions, elements). The canonical Hodgkin–Huxley model is as follows:

$$ I = C_{M} \frac{dV}{dt} + \bar{g}_{K} n^{4} \left( {V - V_{K} } \right) + \bar{g}_{Na} m^{3} h\left( {V - V_{Na} } \right) + \bar{g}_{l} \left( {V - V_{l} } \right) $$

(2)

Key elements of the model are: I (total membrane current as a function of time and voltage), $C_{M}$ (cell membrane capacity per unit), $dV$ (change of membrane potential from resting value), $dt$ (change over time), and $g$‘s (ions such as sodium [$Na$] and potassium [$K$]). Hodgkin and Huxley were able to successfully apply dynamical systems theory in the form of differential equations because they conceptualized the phenomenon of interest—namely, action potentials in the squid giant axon—as essentially a temporal event. From a dynamical perspective, their job became one of identifying the relevant variables responsible for the behavior. In this light, it is easy to see the Hodgkin–Huxley canonical model as an early application of a version of the dynamical hypothesis. While the original dynamical hypothesis is a set of claims concerning cognitive agents, here the concern is physiology. Specifically, Hodgkin and Huxley’s investigative framework was dynamical through and through in that it approached the phenomenon of interest in terms of its being both able to be understood as a dynamical system (i.e., modeled via differential equations) and as being a dynamical system (i.e., defining the action potential as a temporal event).⁶

As with any attempts at modeling complicated phenomena, it can be quite challenging to select the best variables to account for the target of interest. This is especially true with biological entities that usually have features that often interact nonlinearly. Consequently, many biological phenomena produce high-dimensional data. To the uninitiated, the Hodgkin–Huxley model presented above may seem quite complicated due to the appearance of many variables. Even if the model is seemingly complicated, Hodgkin and Huxley (1952) went through many iterations of models before developing the streamlined canonical model presented above. Moreover, defining the model above actually requires defining three of the variables with differential equations of their own, such that the Hodgkin–Huxley model, fully defined, is the following four-dimensional model:

$$ I = C_{M} \frac{dV}{dt} + \bar{g}_{K} n^{4} \left( {V - V_{K} } \right) + \bar{g}_{Na} m^{3} h\left( {V - V_{Na} } \right) + \bar{g}_{l} \left( {V - V_{l} } \right) $$

(3)

where

$$ {\raise0.7ex\hbox{${dn}$} \!\mathord{\left/ {\vphantom {{dn} {dt}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${dt}$}} = \alpha_{n} \left( {1 - n} \right) - \beta_{n} n, $$

(4)

$$ {\raise0.7ex\hbox{${dm}$} \!\mathord{\left/ {\vphantom {{dm} {dt}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${dt}$}} = \alpha_{m} \left( {1 - m} \right) - \beta_{m} m, $$

(5)

$$ {\raise0.7ex\hbox{${dh}$} \!\mathord{\left/ {\vphantom {{dh} {dt}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${dt}$}} = \alpha_{h} \left( {1 - h} \right) - \beta_{h} h $$

(6)

Seeing that the fully defined Hodgkin–Huxley canonical model is four differential equations makes clearer that the model cannot be solved analytically. Moreover, plotting the model along four dimensions creates a phase space plot that is challenging to interpret (Gerstner et al. 2014). Such cases are examples of the work dimensionality reduction can do to facilitate understanding of high-dimensional data.

The FitzHugh–Nagumo model of neuron excitability (FitzHugh 1961; Nagumo et al. 1962) is essentially the product of applying dimensionality reduction to the Hodgkin–Huxley model. Whereas the fully defined Hodgkin–Huxley model is a four-dimensional set of differential equations, the FitzHugh–Nagumo model is a pair of two-dimensional differential equations:

$$ \dot{V} = V - \frac{{V^{3} }}{3} - W + I $$

(7)

$$ \dot{W} = 0.08\left( {V + 0.7 - 0.8W} \right) $$

(8)

What is more, the FitzHugh–Nagumo model includes only three variables: $I$ (stimulus current magnitude), $V$ (cell membrane potential), and $W$ (recovery variable). Whereas the fully defined Hodgkin–Huxley model requires a four-dimensional phase space plot to depict the full range of behavior, the full range of behavior of the FitzHugh–Nagumo model can be depicted by a simpler two-dimensional phase space plot (Fig. 3).

Fig. 3

Phase space plot of FitzHugh–Nagumo model. With just two dimensions—$V$ (membrane potential) and $W$ (recovery variable)—the phase space plot depicts the full range of behavioral trajectories from a range of initial conditions. (Modified and reprinted with permission from Scholarpedia. CC BY-NC-SA 3.0.)

The FitzHugh–Nagumo model captures the full temporal range of neuronal excitation and propagation with two electrochemical properties: potassium and sodium ion flows (Izhikevich and FitzHugh 2006). It is worth noting that he FitzHugh–Nagumo model is less biologically realistic than the Hodgkin–Huxley model because it includes less empirically validated dimensions. With that said, it is still able to capture much of the same key information that the Hodgkin–Huxley model does. Though the Hodgkin–Huxley model is more biologically realistic than the FitzHugh–Nagumo model, only temporal projections of its four-dimensional phase trajectories can be simultaneously observed, which has the consequence of not allowing the model’s solution to be observed via a single plot (Izhikevich and FitzHugh 2006). In other words, a plot of the Hodgkin–Huxley model can depict direction of activity over time (i.e., projections), but not the states that it will settle in. With only two dimensions, the entire solution of the FitzHugh–Nagumo model can be plotted. Consequently, not only is the temporal trajectory of activity depicted (and maintained from the Hodgkin–Huxley model), but so too is the solution, namely, the states that the system settles in (i.e., properties not revealed by plotting the four dimensions of the Hodgkin–Huxley model). Thus, not only does the FitzHugh–Nagumo model capture the key information concerning the properties of excitation and propagation that contribute to single-neuron spiking that the Hodgkin–Huxley model does, but by having its full solution plotted on two dimensions it reveals nonlinearities and feedback that contribute to spiking activity (Izhikevich 2007; Izhikevich and FitzHugh 2006). In that way, the FitzHugh–Nagumo model is a clear example of dimensional reduction methods integrated with dynamical systems theory methods in the history of neuroscience. Specifically, information about the phenomenon of interest—namely, single-neuron activity—that is captured by four dimensions in the Hodgkin–Huxley model is maintained when reduced to the two dimensions “principle components” in the FitzHugh–Nagumo model. It is worth noting that other early applications of PCA in the mind sciences are found in Elman’s work on connectionist models of language (Elman 1991) and in biophysics by Haken and Kelso on self-organization in the brain during behavioral tasks (Kelso and Haken 1995).

I have presented the Hodgkin–Huxley model and FitzHugh–Nagumo model as cases of dynamical systems theory being employed in some of the major achievements in the history of neuroscience. Moreover, the latter model also integrated dimensionality reduction methodology. What I have not done is presented those cases as a means to demonstrate that dynamical approaches provided the only investigative framework employed in the neurosciences, broadly construed. There should be no doubt that mechanistic and reductionistic approaches were common and that such research was successfully conducted without dynamical systems concepts or methods. With that said, the above two cases should make it clear that it is incorrect to view dynamical systems theory as a novel development in contemporary neuroscience (see footnote 4 above). Even the most cutting edge neuroscience research—from microscale genetics to macroscale behavior—with its heavy focus on employing various types of dimensionality reducing methods (Churchland and Abbott 2016; Fan and Markram 2019; Frégnac 2017) have as forerunners research in the mid-1900s that can reasonably be identified as dynamical (Kass et al. 2018). It is in that sense that there is a dynamical renaissance in contemporary neuroscience, and that it is clear that a version of the knowledge hypothesis part of the dynamical hypothesis has turned out to be true, namely, that at least some of the underlying physiology of cognitive systems can be understood as a dynamical system, and not as computational. In the following section, I present representational and dynamical systems explanations of motor control in order to demonstrate how the dynamical renaissance is motivating a reexamination of the necessity of appealing to “representations” in explanations of neural phenomena.

3 W(h)ither representations?

Thus far, I have attempted to make the primarily historical and weaker point that the increased presence of dynamical systems theory in contemporary neuroscience is more akin to a renaissance than a novel introduction. In this section I aim to make a stronger point: along with utilizing concepts and methods, the revival of dynamical systems theory in contemporary neuroscience is driving a reassessment of the necessity of the concept “representation” in explanations of neural phenomena. This point parallels the nature hypothesis part of the dynamical hypothesis—namely, that cognitive agents are dynamical systems—and states that neural systems are dynamical systems. As discussed above, whereas the knowledge hypothesis part of the dynamical hypothesis landed quietly, the nature hypothesis arrived loudly. The reason is that central to the nature hypothesis is the metaphysical claim that cognition is not essentially computational or representational in nature (van Gelder 1995). Given that computations and representations are defining features of the purportedly dominant information-processing frameworks in the mind sciences since at least the cognitive revolution (~ 1950s), it is no wonder that it has been said that it would be either “confusion or brazenness” (Shapiro 2013, pp. 362–363) to reject explaining cognition—or neural systems—in computational and representational terms. In this section, I aim to demonstrate that—although it may indeed be brazen—it is certainly not confused to think that the phenomena investigated by the neurosciences can be explained without appeal to representations. I do so by discussing representational and dynamical accounts of motor control.

3.1 Motor control

Motor control is the ability of a system to generate goal-directed and coordinated movements with the body and environment (Latash et al. 2010). A simple example of motor control is when a monkey is hanging from a tree branch with one hand and reaches for a piece of fruit with the other hand. The goal is to not fall and get something to eat at the same time. What is being coordinated is the body (arms, hands, legs, etc.), location of tree branch in relation to body, and location of fruit in relation to body and tree. There are various theories for understanding motor control, with their own background assumptions, such as artificial intelligence/robotics, ecological, neuroanatomical, and synergetics/self-organization (Turvey and Fonesca 2008). Here, I focus on the traditionally predominant approaches in neuroscience that have focused on the central nervous system (CNS) and sensorimotor transformations (Jordan and Wolpert 2000). In short, these approaches are information-processing frameworks, where the motor system (i.e., limbs, joints, and muscles) receives motor commands (e.g., force, reach, torque adjustments; Diedrichsen 2012) from the controller located in the CNS (Jordan and Wolpert 2000). Moreover, representations and the information they encode are fundamental to this approach. This is admittedly a very general overview of motor control. My aim here is not to provide a thorough introduction to motor control, but to focus on what can broadly be referred to as “representational” and “dynamical systems” approaches to motor control. The presentation of these approaches is intended to demonstrate that the renaissance of dynamical systems theory in contemporary neuroscience is motivating nonrepresentational explanations of various neural phenomena.

3.2 Representational accounts of motor control

There is a long history in neuroscience and related fields (e.g., neurology) during which representations have played a central role in accounts of motor control (for discussion of competing applications of the term in the history of neuroscience, see Chirimuuta 2019). This history includes usages such as: the somatosensory cortex represents the body (e.g., Brecht 2017), neuronal activity patterns represent systematic relationships with body and world (e.g., S1 somatotopic maps; Wilson and Moore 2015), and neurons are vehicles that represent semantic information for goal-directed behavior (Thomson and Piccinini 2018). In many areas of current neuroscience research, “representations” have been cashed out in terms of coding (Brette 2019; Dehaene 2014; Koch and Marcus 2014). As both a literal and metaphorical term, “coding” (including “decoding” and “encoding”) has also come to be the way representations involved in motor control are understood (Shenoy et al. 2013; Thomson and Piccinini 2018). Like “representation,” there are various uses of the term “coding.” As Brette (2019) points out, the phrase “neural coding” appears in over 15,000 papers in a Google Scholar search of literature from the past ten years. For that reason, I will not attempt to provide an all-encompassing definition of “coding” or “neural coding.” Instead, I limit discussion to “coding” in terms of representations involved in motor control.

Given that information-processing approaches have such a large presence in contemporary neuroscience, it is unsurprising that concepts from computer science are appealed to when attempting to explain key claims of the approach, namely, that cognitive and neural systems are computational and representational in nature. As a starting point, motor control from an information-processing perspective can be understood in the following terms:

[T]he motor system can be considered a system whose inputs are the motor commands emanating from the controller within the central nervous system … To determine the behavior of the system in response to this input, an additional set of variables, called state variables, also must be known. For example, in a robotic model of the arm, the motor command would represent the torques generated around the joints and the state variables would be the joint angles and angular velocities. Taken together, the inputs and the state variables are sufficient to determine the future behavior of the system. (Jordan and Wolpert 2000, p. 601; italics in original)

Along those lines, the focus of motor control research in neuroscience has been to explain how such commands and state variables are encoded and decoded (Shenoy et al. 2013). In addition, the primary research target has been single neurons and the ways parameters are coded to control cortical output. From this general approach, single neurons provide the vehicles for encoded and decoded content, such as the content of state variable parameters. Thus, the job of the neuroscientist has been to describe the firing of individual neurons in the motor cortex as a function of various parameters (i.e., state variables) for concurrent or upcoming movements (Shenoy et al. 2013, pp. 340–341).

Consider a standard neuroscience experiment: the instructed-delay task. In this task, experimental subjects (e.g., human, monkey, etc.) are instructed which movements they should make after a cue tells them to make the movement (Kandel et al. 2000). A typical experimental setup involves a subject sitting in a chair in front of a touch screen while behavioral, muscle, and/or neural measurements are recorded. A basic task could involve the subject visually fixating on a green target on the screen and touching it with their hand (Fig. 4a), another red target appears so they know where their movement must be made, and after a delay, the subject is presented with the green target and then moves to the spot where the red target was (Shenoy et al. 2013). One kind of representational account of this event is as follows: The task (i.e., reaching targets with a hand) is encoded (represented) in the controller located in the CNS, which outputs commands to the motor system. The controller incorporates encoded (represented) sensory information as well, namely, visual information in the form of green and red targets. The controller also incorporates information from state variables that have encoded (represented) states of the system itself, such as arm angle, torques around the elbow joint, etc. In view of that story, the neuroscientist working on motor control focuses her research on single neurons by elucidating the relevant state variables encoded and identifying the tuning of those parameters necessary to produce successful movement (Fig. 4b).

Fig. 4

Representational and dynamical systems accounts of motor control. a In an instructed-delay task, a participant begins by focusing on a starting point, such as a green target, is presented another target (e.g., red square), and is instructed to point to the spot the second target was located after being presented with the first target. Behavioral, muscle, and/or neural measurements are recorded during the task. b Representational accounts of motor control traditionally focus on single neurons (e.g., Jordan and Wolpert 2000). The research aim is to identify the firing rate ($r$) of single neurons ($n$) in the motor cortex that describe functions of various parameters ($param_{i}$) that represent concurrent or upcoming movements (Eq. 1). Models of neuronal populations (Eq. 2) can integrate parameter functions defined at the single neuron. Motor commands are encoded in motor neurons via pulses that provide state variable profiles (B, bottom). (C) Dynamical systems accounts of motor control often focus on neural populations. The research aim is to elucidate neural population cortical activity ($\varvec{r}\left( t \right)$) that is mapped onto muscle activity ($\varvec{m}\left( t \right)$), as well as other intermediating circuits ($G\left[ x \right]$), that produce body movements in a manner that achieves the system’s aims (Eq. 3). $\varvec{r}\left( t \right)$ can be defined to capture neural population temporal activity (${\dot{\mathbf{r}}}$) that is determined by local motor cortex circuitry ($h\left( x \right)$) and inputs from other areas of the system (${\mathbf{u}}\left( t \right)$) (Eq. 4). State space plot of rotational dynamics (bottom). Data from Churchland et al. (2012) were reduced via jPCA to two dimensions that capture a significant portion of the neural population’s variance. Here, “a.u.” refers to “arbitrary units,” which is acceptable because the plot depicts the abstract nature of the population’s dynamics and not its actual dynamics in real space. (Modified and reprinted with permission from Pixabay and SVG Silh. CC0 1.0 (A); Modified and reprinted with permission from Eyal et al. (2018). CC BY 4.0 and Sartori et al. (2017). CC BY 4.0 (B); and Modified and reprinted with permission from Prior (2018). CC BY 4.0 and Lebedev et al., (2019). CC BY 4.0 (C).)

Shenoy and colleagues (2013) describe the representational perspective as focused on explaining single-neuron activity in terms of tuning for movement parameters (Shenoy et al. 2013, p. 340). They present the following as the general model adhered to by such approaches:

$$ r_{n} \left( t \right) = f_{n} \left( {param_{1} \left( t \right),param_{2} \left( t \right),. . .} \right) $$

(9)

where the firing rate ($r$) of single neurons ($n$) in the motor cortex are described as functions of various parameters ($param_{i}$) representing concurrent or upcoming movements. If it seems that the number of relevant parameters could be enormous, that is because it is. Part of the reason is because identifying each parameter, as well as defining its tuning, must also take into account covariates such as target locations, limb kinematics, proprioceptor activity, muscular synergies, and more (Shenoy et al. 2013). It is worth pointing out that although the general model defined by Shenoy and colleagues that focuses on single-neuron activity is true of much neuroscience research on motor control, the general idea also applies to research on neuronal populations (e.g., Sartori et al. 2017). In such cases, the general model of neuronal populations contributing to motor control is as follows:

$$ DR_{n} = \frac{1}{{t_{n} - t_{n - 1} }} $$

(10)

where $R$ refers to the parameters encoded in single neurons that code for movement instructions to the body and $D$ refers to the activity of neuronal populations that map to and from the body. Shenoy et al.’s general model of single neurons can be readily incorporated into the population model by defining $R$ as $f_{n} \left( {param_{1} \left( t \right),param_{2} \left( t \right),. . .} \right)$. Thus, even if a model of motor control is focused on neuronal populations, the action—that is, the representational action—remains located in the single neurons that state variables are encoded in. In summary, representational accounts understand motor control as a form of information processing, where movement is controlled beforehand and concurrently, said movements are encoded in single neurons, and neuronal activity is tuned to various parameters (i.e., state variables) that contribute to the action (e.g., limb velocity, joint torque, etc.).

3.3 Dynamical systems accounts of motor control

Although representational accounts of motor control can utilize dynamical systems theory methods (e.g., treating data as continuous and applying differential equations; e.g., Schöner et al. 2016), there can be fundamental differences between them insofar as explaining motor control goes.⁷ First, dynamical systems accounts of motor control focus on neural dynamics, specifically, the dynamics of neural populations (Fig. 4c). This contrasts with representational accounts that focus on the coding (i.e., representation) of movement parameters (e.g., body states, such as limb angles, and world states, such as target location), and how those parameters are tuned in single neurons. Second, the dynamical systems approach focuses on the state of the system producing movement and not what outputs of the system are represented. In other words, the dynamical systems approach is centrally concerned with system dynamics (or rules) that constitute movement (Churchland et al. 2012; Gallego et al. 2017; Michaels et al. 2016) and representational approaches are centrally concerned with how the system codes for current and future movements (Heitmann et al. 2015; Schöner et al. 2016).

One way to begin to understand the dynamical systems approach to motor control is in terms of how it conceptualizes the nervous systems. Whereas the representational approach views the nervous system as, well, a representational system, the dynamical systems approach views the nervous system as a pattern-generating system. The patterns the nervous system generates are aimed at successful movement. A general model for understanding this view of the nervous system is as follows (Shenoy et al. 2013):

$$ \varvec{m}\left( t \right) = G\left[ {\varvec{r}\left( t \right)} \right] $$

(11)

where neural populations of cortical activity ($\varvec{r}\left( t \right)$), are mapped onto muscle activity ($\varvec{m}\left( t \right)$), with other intermediating circuits ($G\left[ x \right]$), to produce body movements in a manner that achieves the system’s aims (Fig. 4c). The variable $\varvec{r}\left( t \right)$ is further defined as the following function:

$$ {{\tau }}{\dot{\mathbf{r}}}\left( t \right) = h\left( {{\mathbf{r}}\left( t \right)} \right) + {\mathbf{u}}\left( t \right) $$

(12)

where neural population over time (${\dot{\mathbf{r}}}$) is determined by local motor cortex circuitry ($h\left( x \right)$) and inputs from other areas of the system (${\mathbf{u}}\left( t \right)$). As such, a key feature of the dynamical systems approach is to elucidate the ways in which movements are driven—that is, determined, constrained, and sustained—by temporal patterns produced by neural populations (Shenoy et al. 2013, p. 341).

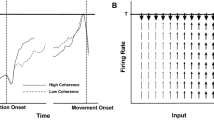
Churchland and colleagues successfully applied this approach to motor control during reaching. For details of the experiment and analyses, I refer readers to the primary source (Churchland et al. 2012; for further discussion by the authors see Shenoy et al. 2013; and for critiques of the study see Lebedev et al. 2019). In short, the authors conducted both single- and multi-unit recordings of four monkeys’ motor and premotor cortex during an instructed-delay task. Although the across-trial firing rate among single neurons exhibited commonly expected dynamics, they also demonstrated “quasi-oscillations patterns” in the form of rotational structure just before movement onset (Churchland et al. 2012, p. 52). The investigators then assessed the neural populations to see if the same rotational structure was exhibited at the population level. Findings at the neural-population level included: rotational dynamics during reaching, rotational dynamics in the same direction across conditions (i.e., variations of the instructed-delay task), rotational dynamics followed from a preparatory state, and the state space of the dynamics are not directly related to the arm movements (Churchland et al. 2012, pp. 52–53). It is important to clarify these findings, especially the fourth. In order to do so, it is necessary to explicate the data analyses a bit.

Churchland and colleagues utilized a dynamical systems theory approach to analyze the data. In doing so, they applied the elements described in Sect. 2 above: a quantitative element that incorporated dimensionality reduction and a qualitative element. In order to quantify the rotational dynamics, they utilized a type of principal components analysis they call “jPCA:”

$$ \dot{x}\left( {t,c} \right) = M_{\text{skew}} x\left( {t,c} \right) $$

(13)

where $\dot{x}\left( {t,c} \right)$ is the population state at time $t$ and condition $c$, and $M_{\text{skew}}$ is a matrix that captures the rotational dynamics (Churchland et al. 2012, p. 54). Datasets were reduced to six dimensions and then analyzed via the jPCA. The jPCA process reduced the datasets to two dimensions that were able to capture a significant portion of the variance. Thus, the population dynamics were plotted on a two-dimensional state space (e.g., Fig. 4c, bottom). As discussed above (Sect. 2), in dynamical systems theory, a state space can be an abstract depiction of dynamics and not a literal depiction of movement in real space (Fig. 1). Accordingly, the state space plots produced from Churchland et al.’s jPCA data are not actual depictions of neural population dynamics, but an abstract depiction of the dynamics, which Churchland and colleagues refer to as “rotational” given their oscillatory nature. In other words, the rotational movement of the dynamics in the state space does not indicate that the real neurons from which the data was collected fire individually or as a population in a circular movement around a center point in physical space. Instead, in terms of the two identified principal components that capture the majority of variance (i.e., jPC₁ and jPC₂), from the preparatory state (red or green circle; Fig. 4c, bottom), the dynamics can be understood as “rotational” in that they begin from a center point, and then their trajectory demonstrates movement away from the center and then back in the direction of the center. It is in that way that the state space is an abstract depiction of the dynamics.⁸ The four findings will be easier to grasp now that the analyses themselves, especially the state space plots, are better understood.

In regard to the first and second findings, the rotational dynamics (i.e., population-scale neural activity) during reaching were statistically the same across the different experimental conditions (i.e., movements to variously-located targets). Third, the various movements during tasks followed from the statistically same preparatory states, namely, the rotational dynamics. What that means is that task movements were the output of regular system dynamics instead of the system representing the desired outcome. That leads to the fourth—and for current purposes the most important—finding, the dynamics depicted by the state space (Fig. 4c, bottom) do not depict (or represent) the real space movements they were implicated in. In short, although the arm movements may look “rotational” as they reach to and from the starting position in real space, the rotational dynamics exhibited by the state space are not representations of the arm movements. They are abstract depictions of the temporal dynamics of the neural populations. Think back to the discussion of the qualitative element of dynamical systems theory approaches discussed above (Sect. 2.1). The phase space plot of pendulum dynamics (Fig. 1b) is not a depiction of the pendulum moving in real space. It is a visual depiction of the abstract nature of the temporal dynamics. Correspondingly, the phase space plot of rotational dynamics (Fig. 4c, bottom) is not a depiction of neural populations activity in real space. It is a visual depiction of the abstract nature of the neural population activity after being reduced to two principal components that account for a significant portion of the original dataset’s variability. As a result, the state space rotational dynamics do not imply that the neural population codes for (or represents) rotational movements.

In summary, dynamical systems accounts understand motor control as a form of pattern generation, where the nervous system does not represent states but drives desired movements. In that way, the nervous system is better thought of as constituting and producing forces that turn out the body’s movements. Furthermore, such an approach is not about accurately representing or encoding state variables but as producing movements that regularly lead to successful outcomes or not. In this way, the dynamical approach to motor control supports the dynamical hypothesis. First, as Churchland and colleagues’ research demonstrates (Churchland et al. 2012; Shenoy et al. 2013) it is a successful application of the elements of dynamical systems theory to fruitful research on neural systems, namely, motor control can be understood as a dynamical system. Second, that research demonstrates that core topics in neuroscience can be investigated, explained, and understood without appeal to information-processing frameworks, especially without invoking representations as key features of complex and goal-directed activity. That is to say, motor control can be understood as a dynamical system. I do not intend for this argument to lead to the conclusion that representations can wither away completely from neuroscience research, or from work on motor control. I do intend for this argument to motivate the claim that representations—as well as information-processing approaches in general—need not be the unquestioned go to in neuroscience research. Whither representations in neuroscience? Not eliminated, but not absolutely necessary either.

4 Conclusion

Dynamical systems theory is becoming increasingly popular in contemporary neuroscience (for a small sample see Breakspear 2017; Deco et al. 2017; Honey and Sporns 2008; Izhikevich 2007; Rabinovich et al. 2006; Sussillo 2014). In spite of the increased prominence in neuroscience research, discussion of dynamical systems theory in neuroscience among philosophers has been minimal (exceptions to this include Chemero and Silberstein 2008; Chirimuuta 2018; Favela 2019, 2020; Ross 2015). This is slightly odd given significant discussion of dynamical systems in cognitive science by philosophers (see Sect. 1 above). Perhaps, this is the case because philosophers have assumed that arguments applicable in cognitive science apply broadly to other mind sciences such as neuroscience. Yet, the place of dynamical systems theory in neuroscience is unique to that of cognitive science. Significant discussion among cognitive scientists and philosophers on the topic of dynamical systems theory began in the 1990s. But in neuroscience, dynamical systems theory was central in the mid-1900s, faded a bit, and then recently shows signs of increased applicability. For that reason alone, one could think philosophers (especially in history and philosophy of science; though, as mentioned above, see Chirimuuta 2019) would be more interested in understanding dynamical systems theory in the history of neuroscience. I hope to have motivated the worth of such a project here.

In addition, I have aimed in this paper to motivate viewing research in contemporary neuroscience from a dynamical systems theory approach as supporting a version of the dynamical hypothesis. Whereas the original dynamical hypothesis (e.g., van Gelder 1995) focused on cognitive agents, the version I have in mind is broader and includes the substrates of cognitive systems as well. Accordingly, I argued that the concepts and methods of dynamical systems theory have successfully been applied to neural systems in contemporary neuroscience. Moreover, I have argued that such approaches have also motivated understanding neural systems as dynamical systems, which includes not requiring appeal to computations or representations to explain or understand those systems. Taken together, the historical claim—that dynamical approaches were prominent in the mid-1900s—and the critical claim—that representations are unnecessary in at least some core areas of research—demonstrate that the dynamical hypothesis is undergoing a renaissance in contemporary neuroscience.