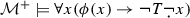Abstract
The infinitary function of the truth predicate consists in its ability to express infinite conjunctions and disjunctions. A transparency principle for truth states the equivalence between a sentence and its truth predication; it requires an introduction principle—which allows the inference from “snow is white” to “the sentence ‘snow is white’ is true”—and an elimination principle—which allows the inference from “the sentence ‘snow is white’ is true” to “snow is white”. It is commonly assumed that a theory of truth needs to satisfy a transparency principle to fulfil the infinitary function. Picollo and Schindler (Erkenntnis 83:899–928, 2017) argue against this idea. They prove that, given certain assumptions, an elimination principle is sufficient for the purpose. Then, they pose a challenge: to show why we should incorporate introduction principles to our theory of truth. In this essay I take on the challenge. I show that, given the authors’ assumptions, an introduction principle is also sufficient to perform the infinitary function.
Similar content being viewed by others
Notes
It is not logical simpliciter because a theory of truth requires a background theory about the objects to which truth is applied (e.g. sentences, Gödel codes thereof, propositions), that is, a theory of syntax.
In the literature, Peano or Robinson arithmetic are usually taken as syntax theory. At any case, we assume that \(\Sigma \) interprets some decent amount of arithmetic.
The schema and the pair of rules are equivalent in classical logic. However, the equivalence does not hold in every non-classical system, so there could be reasons to prefer one transparency principle over the other.
A truth theory is said to be type-free if it proves sentences of the form \(T\,\ulcorner T\,\ulcorner \phi \urcorner \urcorner \).
By “Let \(\phi (x)\) be a predicate of \({\mathcal {L}}_T\)-sentences”, I mean that the syntax theory \(\Sigma \) proves the (formalisation of) the claim “For all x, if \(\phi (x)\) then x is a sentence of \({\mathcal {L}}_T\)”. (I follow Picollo and Schindler on this assumption (p. 907).)
In their article, Picollo and Schindler show that an elimination principle is sufficient to express infinite disjunctions relative to the finite-axiomatisation approach in Halbach (1999). For the sake of uniformity, I make the argument from this section relative to the approach defined in Sect. 2.1. Accordingly, I adapt assumptions (a) and (b) by Halbach: in the original paper, they are restricted to infinite conjunctions and disjunctions of T-free sentences.
We use
 to denote the negation function that, applied to (the code of) a formula \(\phi \), gives (the code of) \(\lnot \phi \). We assume that the base theory \(\Sigma \) proves
to denote the negation function that, applied to (the code of) a formula \(\phi \), gives (the code of) \(\lnot \phi \). We assume that the base theory \(\Sigma \) proves 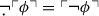 for any formula \(\phi \) of \({\mathcal {L}}_T\).
for any formula \(\phi \) of \({\mathcal {L}}_T\).This is, the inference from \(s=t\) and \(\phi (s)\) to \(\phi (t)\) holds for every formula \(\phi (x)\) and terms s, t.
I do not assume, and do not attribute to Picollo and Schindler, the view that any sentence expresses the conjunction of all the \(\phi \)s just in case it proves all the consequences of the conditionals \(\phi (\ulcorner \psi \urcorner )\rightarrow \psi \). (I thank an anonymous reviewer for suggesting me to clarify this.) Two points are worth mentioning. First, Inf-C and Inf-C* differ from a contradiction in that, if T is a primitive predicate, they do not prove the conditionals mentioned by classical logic alone. Second, Inf-C and Inf-C* differ from most sentences in that, when combined with the appropriate half of a transparency principle, they have some interesting properties regarding the conservativity of the theory of truth (see Sect. 3.4).
That is to say, suppose that \(\forall x(\chi (x)\rightarrow (x=\ulcorner \psi _{1}\urcorner \vee ...\vee x=\ulcorner \psi _{n}\urcorner ))\).
It is noteworthy that the counterarguments do not (and are not intended to) answer the objections A–D ‘in their own spirit’. The counterarguments focus on the expressive functions of the truth predicate. They show that certain (sets of) sentences can be expressed by means of an elimination (introduction) principle alone. In contrast, the objections focus on the inferential roles of truth. They point to certain inferences that seem to be valid but, without suitable principles, do not hold. Since both Picollo and Schindler’s paper and this essay focus strictly on the expressive functions of truth, this misappropriation of the objections does not constitute a problem.
A formula \(\phi (x)\) weakly represents a set A in a theory \(\Gamma \) just in case, for every object a denoted by a term \({\overline{a}}\), we have \(\Gamma \vdash \phi ({\overline{a}})\) if and only if \(a\in A\).
The outer logic of a theory \(\Gamma \subseteq L_T\) is the set of its theorems. The inner logic is the set of sentences \(\phi \) such that \(\Gamma \) proves \(T\ulcorner \phi \urcorner \).
A liar is a sentence \(\lambda \) s.t. our syntax theory proves \(\lambda \leftrightarrow \lnot T\,\ulcorner \lambda \urcorner \).
If we regard “All theorems of \(\Gamma \) are true” as somehow similar to “All theorems of \(\Gamma \) are non-false”, it is probably because of the intuitive validity of the rule that commutes truth and negation:
$$\begin{aligned} \lnot T\,\ulcorner \phi \urcorner \dashv \vdash T\,\ulcorner \lnot \phi \urcorner \end{aligned}$$Now, the left-to-right direction of this rule together with an elimination principle imply transparency; if the background logic is classical, this means triviality. Thus, the intuitive appeal of \(\text {GRP}^{*}_{\Gamma }\) seems to rely on a rule that is not (fully) admissible in the framework.
I thank an anonymous reviewer for encouraging me to address the subject of this section.
Heck advances another objection against Halbach’s account. The author argues that the truth predicate serves certain quasi-logical expressive functions which (i) are not plausibly described as that of expressing infinite conjunctions and disjunctions and (ii) require principles stronger than disquotation. This may be pressing for Halbach. However, I do not assume either that what I called the infinitary function exhausts the expressive utility of the truth predicate, or that a disquotation principle provides “a complete description of truth” (Halbach 1999, p. 1). Hence, I reckon that Heck’s objection does not affect per se the semidisquotational proposals addressed. It would be coherent to say that, while an introduction or elimination principle is sufficient to express infinite conjunctions and disjunctions, a complete theory of truth must ultimately appeal to principles which go beyond disquotation.
References
Beall, J. (2009). Spandrels of truth. Oxford: Oxford University Press.
Cobreros, P., et al. (2013). Reaching transparent truth. Mind, 122, 841–866.
Da Ré, Bruno (2020). Structural weakening and paradoxes. Manuscript. Retrieved at https://www.researchgate.net/publication/348517688_Structural_weakening_and_paradoxes.
Field, H. (2008). Saving truth from paradox. New York: Oxford University Press.
Gupta, A. (1993). A critique of de ationism. Philosophical Topics, 21, 57–81.
Halbach, V. (2011). Axiomatic Theories of Truth. Cambridge: Cambridge University Press.
Halbach, V. (1999). Disquotationalism and infinite conjunctions. Mind, 108, 1–22.
Heck, Richard K. (2004) Truth and Disquotation. In Synthese 142. (Originally published under the name “Richard G. Heck, Jr”.), pp. 317–352.
Horsten, L. (2011). The Tarskian turn: De ationism and axiomatic truth. Cambridge: MIT press.
Horwich, P. (1998). Truth (2nd ed.). Oxford: Blackwell.
Kripke, S. (1975). Outline of a theory of truth. Journal of Philosphy, 72, 690–716.
Leeds, S. (1978). Theories of reference and truth. Erkenntnis, 13, 111–129.
Leitgeb, H. (2007). What theories of truth should be like (but cannot be). Philosophy Compass, 2, 276–290.
Picollo, L., & Schindler, T. (2019). De ationism and The Function of Truth. Philosophical Perspectives, 32, 326–351.
Picollo, L., & Schindler, T. (2017). Disquotation and infinite conjunctions. Erkenntnis, 83, 899–928.
Priest, G. (2006). In contradiction. New York: Oxford University Press.
Putnam, H. (1978). Meaning and the moral sciences. London: Routledge.
Quine, W. V. O. (1970). Philosophy of logic. Cambridge: Harvard University Press.
Rosenblatt, L. (2019). Noncontractive classical logic. Notre Dame Journal of Formal Logic, 60, 559–585.
Tarski, A. (1935). The concept of truth in formalized languages. In J. Corcoran (Ed.), Logic, Semantics, Metamathematics (pp. 152–278). Oxford: Clarendon press.
Zardini, E. (2011). Truth without contra(di)ction. Review of Symbolic Logic, 4, 498–535.
Acknowledgements
Earlier versions of this paper have been presented in 2018 at the Work in Progress Seminar of the Buenos Aires Logic Group (Buenos Aires, Argentina), also in 2018 at the National University of Rosario (Rosario, Argentina), and in 2019 at the Mathematical Philosophy Seminar of the Munich Center for Mathematical Philosophy (Munich, Germany); I would like to thank the attendees of these talks for their valuable feedback. I am grateful to Bruno Da Ré, Lavinia Picollo, Lucas Rosenblatt, Thomas Schindler and Diego Tajer for their help and guidance in the preparation of this paper. Finally, I would like to thank an anonymous reviewer of this journal, whose suggestions contributed to a significant improvement of the original draft.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Recall that \({\mathcal {L}}\) contains a term \(\ulcorner \sigma \urcorner \) denoting \(\sigma \) (perhaps via some coding) for each expression \(\sigma \) of \({\mathcal {L}}_T\). Suppose our base theory \(\Sigma \subseteq {\mathcal {L}}\) is classical. Let \(\phi (y)\) be a predicate of sentences of \({\mathcal {L}}\).
Proof of Proposition 10
Define \(\Sigma '\) as \(\Sigma +\{\phi (\ulcorner \psi \urcorner )\rightarrow \psi :\psi \in {\mathcal {L}}\}\) and define \(\Gamma '\) as \(\Gamma +\forall x(\phi (x)\rightarrow Tx)\). We show that \(\Sigma '\) and \(\Gamma '\) have the same T-free consequences.
Let \(\chi \in {\mathcal {L}}\). Assume that \(\Sigma '\vdash \chi \). By the argument from Sect. 2.1 and the fact that \(\Sigma \) is classical, \(\Gamma '\vdash \chi \). For the converse, we will use the following lemma:
Lemma 12
Any model \({\mathcal {M}}\) of \(\Sigma '\) can be expanded to a model \({\mathcal {M}}^+\) of \(\,\Gamma '\).
Proof
If \(\Sigma '\) has no models, the Lemma holds trivially. So, let \({\mathcal {M}}=\langle D,I \rangle \) be a model where D is the domain and I the interpretation function, and suppose that \({\mathcal {M}}\models \Sigma '\). Define \({\mathcal {M}}^+=\langle D,I^+ \rangle \) to be the expansion of \({\mathcal {M}}\) s.t. \(I^+(T)=\{I(\ulcorner \psi \urcorner ):{\mathcal {M}}\models \phi (\ulcorner \psi \urcorner )\}\). We prove that \({\mathcal {M}}^+\vDash \Gamma '\).
-
(a)
Let \(\delta \in {\mathcal {L}}_T\). Assume \({\mathcal {M}}^+\models T\ulcorner \delta \urcorner \). Then, \(I(\ulcorner \delta \urcorner )\in \{I(\ulcorner \psi \urcorner ): {\mathcal {M}}\models \phi (\ulcorner \psi \urcorner )\}\), and hence \({\mathcal {M}}\models \phi (\ulcorner \delta \urcorner )\). Besides, \({\mathcal {M}}\models \phi (\ulcorner \delta \urcorner )\rightarrow \delta \), so \({\mathcal {M}}\models \delta \). \({\mathcal {M}}^+\) expands \({\mathcal {M}}\), so \({\mathcal {M}}^+\models \delta \). Therefore, \({\mathcal {M}}^+\models T\ulcorner \delta \urcorner \rightarrow \delta \).
-
(b)
Let s be any map from the variables in \({\mathcal {L}}_T\) to D. Let \(s'\) differ from s at most at variable x. Assume \({\mathcal {M}}^+,s'\models \phi (x)\). \(\phi (y)\) is a predicate of sentences of \({\mathcal {L}}\) and \({\mathcal {M}}^+\) expands \({\mathcal {M}}\). Thus, \(s'(x)\in \{I(\ulcorner \psi \urcorner ):{\mathcal {M}}\models \phi (\ulcorner \psi \urcorner )\}\). Hence, \({\mathcal {M}}^+,s'\models Tx\). Therefore, \({\mathcal {M}}^+,s'\models \phi (x)\rightarrow Tx\). Map \(s'\) was arbitrary. Thus, \({\mathcal {M}}^+,s\models \forall x(\phi (x)\rightarrow Tx)\). Besides, \(\forall x(\phi (x)\rightarrow Tx)\) is a sentence, so \({\mathcal {M}}^+\models \forall x(\phi (x)\rightarrow Tx)\).
\(\square \)
Assume that \(\Gamma '\vdash \chi \). Suppose, for reductio, that \(\Sigma '\nvdash \chi \). Then, there is a model \({\mathcal {M}}\) of \(\Sigma '\) s.t. \({\mathcal {M}}\not \models \chi \). By our Lemma, there is an expansion \({\mathcal {M}}^+\) s.t. \({\mathcal {M}}^+\models \Sigma '\cup \Gamma '\). \({\mathcal {M}}^+\not \models \chi \), because \({\mathcal {M}}^+\) expands \({\mathcal {M}}\) and \(\chi \in {\mathcal {L}}\). But \({\mathcal {M}}^+\models \chi \), because \({\mathcal {M}}^+\models \Gamma '\). A contradiction. Hence, \(\Sigma '\vdash \chi \). \(\square \)
Proof of Proposition 11
Define \(\Sigma '\) as \(\Sigma +\{\phi (\ulcorner \psi \urcorner )\rightarrow \psi :\psi \in {\mathcal {L}}\}\) and define \(\Gamma '\) as  . We show that \(\Sigma '\) and \(\Gamma '\) have the same T-free consequences.
. We show that \(\Sigma '\) and \(\Gamma '\) have the same T-free consequences.
Let \(\chi \in {\mathcal {L}}\). Assume that \(\Sigma '\vdash \chi \). By the argument from Sect. 3.1 and the fact that \(\Sigma \) is classical, \(\Gamma '\vdash \chi \). For the converse, we will use the following lemma:
Lemma 13
Any model \({\mathcal {M}}\) of \(\Sigma '\) can be expanded to a model \({\mathcal {M}}^+\) of \(\,\Gamma '\).
Proof
Again, if \(\Sigma '\) has no models, the Lemma holds trivially. So let \({\mathcal {M}}=\langle D,I \rangle \) be a model and suppose that \({\mathcal {M}}\models \Sigma '\). Define \({\mathcal {M}}^+=\langle D,I^+ \rangle \) to be the expansion of \({\mathcal {M}}\) s.t. \(I^+(T)=\{I(\ulcorner \psi \urcorner ):\psi \in {\mathcal {L}}_T\} \setminus \{I(\ulcorner \lnot \psi \urcorner ):{\mathcal {M}}\models \phi (\ulcorner \psi \urcorner )\}\). We prove that \({\mathcal {M}}^+\vDash \Gamma '\).
-
(a)
Let \(\delta \in {\mathcal {L}}_T\). Assume \({\mathcal {M}}^+\models \delta \). Then, \(I(\ulcorner \delta \urcorner )\notin \{I(\ulcorner \lnot \psi \urcorner ):{\mathcal {M}}\models \phi (\ulcorner \psi \urcorner )\}\). (Assume the opposite. Then, there is a \(\xi \in {\mathcal {L}}\) s.t. \(\delta \) is identical to \(\lnot \xi \) and \({\mathcal {M}}\models \phi (\ulcorner \xi \urcorner )\). \({\mathcal {M}}\models \phi (\ulcorner \xi \urcorner )\rightarrow \xi \), so \({\mathcal {M}}\models \xi \). \({\mathcal {M}}^+\) expands \({\mathcal {M}}\), so \({\mathcal {M}}^+\models \xi \). Thus, \({\mathcal {M}}^+\not \models \delta \). A contradiction.) Hence, \({\mathcal {M}}^+\models T\ulcorner \delta \urcorner \). Therefore, \({\mathcal {M}}^+\models \delta \rightarrow T\ulcorner \delta \urcorner \).
-
(b)
Let s be any map from the variables in \({\mathcal {L}}_T\) to D. Let \(s'\) differ from s at most at variable x. Assume \({\mathcal {M}}^+,s'\models \phi (x)\). \(\phi (y)\) is a predicate of sentences of \({\mathcal {L}}\) and \({\mathcal {M}}^+\) expands \({\mathcal {M}}\). Thus,
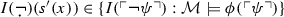 . Hence,
. Hence, 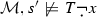 . Therefore,
. Therefore, 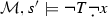 and
and 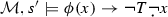 . Map \(s'\) was arbitrary. Thus,
. Map \(s'\) was arbitrary. Thus, 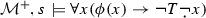 . Besides,
. Besides, 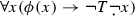 is a sentence, so
is a sentence, so 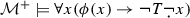
\(\square \)
The proof continues as the analogous part of the proof of Proposition 10, but using Lemma 13 instead of Lemma 12. \(\square \)
Rights and permissions
About this article
Cite this article
Fiore, C. Semidisquotation and the infinitary function of truth. Erkenn 88, 851–866 (2023). https://doi.org/10.1007/s10670-020-00372-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-020-00372-8




 to denote the negation function that, applied to (the code of) a formula
to denote the negation function that, applied to (the code of) a formula 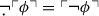 for any formula
for any formula 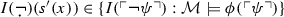 . Hence,
. Hence, 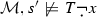 . Therefore,
. Therefore, 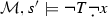 and
and 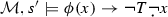 . Map
. Map 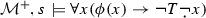 . Besides,
. Besides, 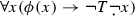 is a sentence, so
is a sentence, so