Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-06-09T11:27:27.898Z Has data issue: false hasContentIssue false
  • English
  • Français

KEISLER’S THEOREM AND CARDINAL INVARIANTS

Published online by Cambridge University Press:  18 November 2022

TATSUYA GOTO
TATSUYA GOTO*
Affiliation:
GRADUATE SCHOOL OF SYSTEM INFORMATICS KOBE UNIVERSITY ROKKO-DAI 1-1, NADA, KOBE 657-8501, JAPAN
*
E-mail: 202x603x@stu.kobe-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider several variants of Keisler’s isomorphism theorem. We separate these variants by showing implications between them and cardinal invariants hypotheses. We characterize saturation hypotheses that are stronger than Keisler’s theorem with respect to models of size 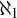$\aleph _1$ and 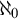$\aleph _0$ by 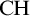$\mathrm {CH}$ and 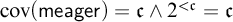$\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land 2^{<\mathfrak {c}} = \mathfrak {c}$ respectively. We prove that Keisler’s theorem for models of size 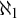$\aleph _1$ and 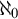$\aleph _0$ implies 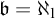$\mathfrak {b} = \aleph _1$ and 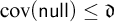$\operatorname {cov}(\mathsf {null}) \le \mathfrak {d}$ respectively. As a consequence, Keisler’s theorem for models of size 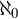$\aleph _0$ fails in the random model. We also show that for Keisler’s theorem for models of size 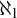$\aleph _1$ to hold it is not necessary that $\operatorname {cov}(\mathsf {meager})$ equals 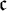$\mathfrak {c}$.

Type
Article
Information
The Journal of Symbolic Logic , Volume 89 , Issue 2 , June 2024 , pp. 905 - 917
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, U., Proper forcing , Handbook of Set Theory , Springer, Cham, 2010, pp. 333–394.10.1007/978-1-4020-5764-9_6CrossRefGoogle Scholar
Bartoszyński, T. and Judah, H., Set Theory: On the Structure of the Real Line , CRC Press, Boca Raton, 1995.10.1201/9781439863466CrossRefGoogle Scholar
Bell, J. L. and Slomson, A. B., Models and Ultraproducts: An Introduction , Courier Corporation, Chelmsford, 2006.Google Scholar
Blass, A., Combinatorial cardinal characteristics of the continuum , Handbook of Set Theory , Springer, Cham, 2010, pp. 395–489.10.1007/978-1-4020-5764-9_7CrossRefGoogle Scholar
Ellentuck, E. and Rucker, R. V. B., Martin’s axiom and saturated models . Proceedings of the American Mathematical Society , vol. 34 (1972), no. 1, pp. 243–249.Google Scholar
Golshani, M. and Shelah, S., The Keisler–Shelah isomorphism theorem and the continuum hypothesis , Fundamenta Mathematicae , to appear, 2022.Google Scholar
Keisler, H. J., Ultraproducts and elementary classes , Ph.D. thesis, University of California, Berkeley, 1961.CrossRefGoogle Scholar
Klausner, L. D. and Mejía, D. A., Many different uniformity numbers of Yorioka ideals . Archive for Mathematical Logic , vol. 61 (2022), no. 5, pp. 653–683.CrossRefGoogle Scholar
Shelah, S., Vive la différence I: Nonisomorphism of ultrapowers of countable models , Set Theory of the Continuum , Springer, Cham, 1992, pp. 357–405.10.1007/978-1-4613-9754-0_20CrossRefGoogle Scholar