Abstract
Inquisitive first order logic  is an extension of first order classical logic, introducing questions and studying the logical relations between questions and quantifiers. It is not known whether
is an extension of first order classical logic, introducing questions and studying the logical relations between questions and quantifiers. It is not known whether  is recursively axiomatizable, even though an axiomatization has been found for fragments of the logic (Ciardelli, 2016). In this paper we define the \(\mathsf {ClAnt}\)—classical antecedent—fragment, together with an axiomatization and a proof of its strong completeness. This result extends the ones presented in the literature and introduces a new approach to study the axiomatization problem for fragments of the logic.
is recursively axiomatizable, even though an axiomatization has been found for fragments of the logic (Ciardelli, 2016). In this paper we define the \(\mathsf {ClAnt}\)—classical antecedent—fragment, together with an axiomatization and a proof of its strong completeness. This result extends the ones presented in the literature and introduces a new approach to study the axiomatization problem for fragments of the logic.
Similar content being viewed by others
1 Introduction
Inquisitive semantics (Ciardelli et al. 2018) is a semantic framework that aims to represent statements and questions uniformly in a logical system and to analyze logical relations between them. Inquisitive first order logic  is the inquisitive counterpart of classical first order logic. In particular, it extends the usual first order language by introducing question-forming operators to represent alternative questions (e.g.,
is the inquisitive counterpart of classical first order logic. In particular, it extends the usual first order language by introducing question-forming operators to represent alternative questions (e.g.,  , which stands for “Does P hold or does Q hold?”) and witness questions (e.g.,
, which stands for “Does P hold or does Q hold?”) and witness questions (e.g.,  , which stands for “What is an element with property P?”).
, which stands for “What is an element with property P?”).
This augmented language captures concepts specific to questions—such as answerhood and dependency between questions—through the entailment of the logic; and it allows to study the complexity of these concepts from a formal point of view: for example, is the dependency between questions recursively enumerable or compact? An effective way to tackle these questions is to characterize the entailment in terms of some fundamental principles and rules, that is, to axiomatize the logic.
Although a recursive axiomatization has been found for several propositional inquisitive logics (Ciardelli 2014; Ciardelli et al. 2020; Ciardelli and Roelofsen 2011; Punčochář 2015, 2019; Katsuhiko 2011), it is still not known whether  admits one. A sound natural deduction system for it has been proposed in Ciardelli (2016, Ch. 4), together with a conjecture of its completeness, which remains open. Ciardelli (2016, Ch. 4) it is also shown that two fragments of the logic—the mention-some fragment
admits one. A sound natural deduction system for it has been proposed in Ciardelli (2016, Ch. 4), together with a conjecture of its completeness, which remains open. Ciardelli (2016, Ch. 4) it is also shown that two fragments of the logic—the mention-some fragment  and the mention-all fragment \({\mathcal {L}}_{\forall }\)—can be recursively axiomatized. This leads to the natural question whether there are other interesting fragments which are axiomatizable, and whether we can find general techniques to axiomatize them. This paper introduces the classical antecedent fragment \(\mathsf {ClAnt}\), which extends \({\mathcal {L}}_{\forall }\) and
and the mention-all fragment \({\mathcal {L}}_{\forall }\)—can be recursively axiomatized. This leads to the natural question whether there are other interesting fragments which are axiomatizable, and whether we can find general techniques to axiomatize them. This paper introduces the classical antecedent fragment \(\mathsf {ClAnt}\), which extends \({\mathcal {L}}_{\forall }\) and  , and a new approach to the completeness problem applicable to \(\mathsf {ClAnt}\), giving a positive answer to the first question and insights on the second.
, and a new approach to the completeness problem applicable to \(\mathsf {ClAnt}\), giving a positive answer to the first question and insights on the second.
\(\mathsf {ClAnt}\) can be intuitively characterized as the fragment where questions are not allowed in the antecedent of an implication. This fragment is particularly interesting since it contains—modulo logical equivalence—all formulas corresponding to natural language statements and several classes of formulas corresponding to natural language questions: for example polar questions (“Will Joey come to the party?”), alternative questions (“Is Joey coming to the party or is Chandler coming?”), mention-some and mention-all questions (“What is an instance of a person coming to the party?”, “Who is coming to the party?”), and their conditional versions (“If Chandler comes to the party, will Joey come to the party too?”). We prove that the natural deduction system proposed for  in Ciardelli (2016), restricted to \(\mathsf {ClAnt}\), provides a sound and strongly complete axiomatization of
in Ciardelli (2016), restricted to \(\mathsf {ClAnt}\), provides a sound and strongly complete axiomatization of  validities in the fragment.
validities in the fragment.
The paper is organized as follows: In Sect. 2 we present  and some basic properties we will use throughout the paper; in Sect. 3 we introduce the \(\mathsf {ClAnt}\) fragment of the logic; in Sect. 4 we study a deductive system suitable to capture entailment between \(\mathsf {ClAnt}\) formulas and show some of its main properties; Sect. 5 is devoted to showing the main result of the paper, that is, the completeness of the deductive system introduced. We conclude with some remarks and future research directions in Sect. 7.
and some basic properties we will use throughout the paper; in Sect. 3 we introduce the \(\mathsf {ClAnt}\) fragment of the logic; in Sect. 4 we study a deductive system suitable to capture entailment between \(\mathsf {ClAnt}\) formulas and show some of its main properties; Sect. 5 is devoted to showing the main result of the paper, that is, the completeness of the deductive system introduced. We conclude with some remarks and future research directions in Sect. 7.
2 Preliminaries
In this section we briefly present first order inquisitive logic ( ) and state the results we will use in this paper. An extensive introduction on the topic is presented in Ciardelli (2016, Ch. 4).
) and state the results we will use in this paper. An extensive introduction on the topic is presented in Ciardelli (2016, Ch. 4).
We start by fixing some notational conventions. With a first order signature we will refer to a finite or countable setFootnote 1
where \(R_0, R_1, \dots \) and \(f_0, f_1, \dots \) are formal symbols, referred to as relation symbols and \(function symbols \) respectively. Each symbol comes with an assigned arity, that is, the number of arguments of its interpretation in a model. We will typically use the symbols P, Q, \(P'\), \(P_1\)...for relation symbols of arity 1 (also called unary relation symbols), and the symbols c, \(c'\), \(c_1\)...for function symbols of arity 0 (also called constants).
We fix a countable set of formal symbols \({{\,\mathrm{\mathrm {\mathbf {Var}}}\,}}\), simply referred to as the variables. We will typically use the symbols x, y, z, \(x'\), \(x_1\)...to indicate elements of \({{\,\mathrm{\mathrm {\mathbf {Var}}}\,}}\). With terms of the signature \(\varSigma \) (or simply terms when \(\varSigma \) is clear from the context) we refer to the standard inductively defined notion of first order term: either a constant in \(\varSigma \), a variable in \({{\,\mathrm{\mathrm {\mathbf {Var}}}\,}}\) or a formal combination \(f(t_1,\dots ,t_n)\) where f is a function symbol of arity n and \(t_1,\dots ,t_n\) are terms previously defined. We will typically use the symbols t, \(t'\), \(t_1\)...to indicate terms. Closed terms (i.e., terms not containing occurrences of variables) will play a special role in the rest of the paper: We indicate with \({\mathcal {T}}_{\varSigma }\) the set of closed terms of the signature \(\varSigma \).
We are now ready to introduce  . The syntax of the logic is obtained by augmenting the syntax of first order logic with additional operators, i.e. inquisitive disjunction
. The syntax of the logic is obtained by augmenting the syntax of first order logic with additional operators, i.e. inquisitive disjunction  inquisitive existential quantifier
inquisitive existential quantifier  .
.
Definition 1
(Syntax of
 ) Fix a first order signature
\(\varSigma \). Formulas of
) Fix a first order signature
\(\varSigma \). Formulas of
 are generated by the following grammar:
are generated by the following grammar:

where R is a relation symbol from \(\varSigma \) and \(t_1,\dots ,t_n\) are terms of the signature \(\varSigma \). The concepts of free and bound occurrences of a variable, of closed formula, etc. are analogous to those of first order logic. Notice that here we are not considering the equality symbol as part of the syntax; for a treatment of the language with equality, see Sect. 6.
We introduce the following shorthands:Footnote 2

As noticed before, the syntax of  is an extension of the syntax of first order logic. This suggests the following definition.
is an extension of the syntax of first order logic. This suggests the following definition.
Definition 2
(Classical formula) A classical formula is a formula not containing the symbols

 .
.
We will usually refer to classical formulas with the symbols \(\alpha ,\beta , \gamma \)—whereas we will use \(\varphi , \psi , \chi \) for arbitrary formulas. Notice that if \(\alpha \) and \(\beta \) are classical formulas, then so are \(\lnot \alpha \), \(\alpha \vee \beta \) and \(\exists x. \alpha \).
There are two motivations to adopt this evocative naming convention: firstly, entailment between classical formulas in
 coincides with first order logic entailment (this will be clarified by Lemma 10); secondly, the natural language interpretation of classical formulas is the same as the conventional one for their first order counterparts. For instance the statement “If Ross is coming to the party, then everyone is coming too” is represented by the classical formula
\(C(r) \rightarrow \forall x. C(x)\).
coincides with first order logic entailment (this will be clarified by Lemma 10); secondly, the natural language interpretation of classical formulas is the same as the conventional one for their first order counterparts. For instance the statement “If Ross is coming to the party, then everyone is coming too” is represented by the classical formula
\(C(r) \rightarrow \forall x. C(x)\).
The new operators 
 are used to introduce questions and logical relations between them into the scope of the system. Inquisitive disjunction introduces alternative questions into the picture, such as “Will Joey come to the party?”, corresponding to the formula ?C(j) ; while inquisitive existential quantifier is used to introduce witness questions, such as “What is an instance of a person coming to the party?” corresponding to the formula
are used to introduce questions and logical relations between them into the scope of the system. Inquisitive disjunction introduces alternative questions into the picture, such as “Will Joey come to the party?”, corresponding to the formula ?C(j) ; while inquisitive existential quantifier is used to introduce witness questions, such as “What is an instance of a person coming to the party?” corresponding to the formula  . A more detailed account of this intuition is given in Ciardelli (2016, Ch. 4).
. A more detailed account of this intuition is given in Ciardelli (2016, Ch. 4).
Since we shifted our attention from statements to sentences, we need to generalize the semantics of classical first order logic also to encompass questions. The approach adopted in  is to move from a truth-based account to an information-based one, as the latter allows us to study logical relations between statements and questions in a uniform way. To do so, we need to introduce a suitable concept of model to represent information.
is to move from a truth-based account to an information-based one, as the latter allows us to study logical relations between statements and questions in a uniform way. To do so, we need to introduce a suitable concept of model to represent information.
Definition 3
(Information model) An information model \(\mathcal {M}\) is a tuple
where W is a set—called the set of worlds of \(\mathcal {M}\)—and \(M_w\) are first order modelsFootnote 3 over the signature \(\varSigma \) such that:
-
The models \(M_w\) (with \(w\in W\)) have the same domain D—called the domain of \(\mathcal {M}\);
-
The interpretation of each function symbol f of arity n is the same function \(f^{\mathcal {M}}: D^n \rightarrow D\) for each \(M_w\) (with \(w\in W\)). This includes the interpretation of constant symbols, that is, functions of arity 0.
For a relation symbol R, we indicate with \(R_{w}\) the interpretation of R in the first order model \(M_w\).
We call a function \(g: {{\,\mathrm{\mathrm {\mathbf {Var}}}\,}}\rightarrow D\) an assignment over the domain D. As a shorthand, we write \(g[x\mapsto d]\) for the assignment that maps the variable \(x\in {{\,\mathrm{\mathrm {\mathbf {Var}}}\,}}\) to the element \(d\in D\), and otherwise coincides with g.
Given a term t (possibly containing free variables), we indicate with \(t^{\left\langle \mathcal {M},g \right\rangle }\) the element corresponding to t, computed recursively in a standard way—notice that \(t^{\left\langle \mathcal {M},g \right\rangle }\) is well defined, since the valuation of constant and function symbols is the same for every model \(M_w\) within the information model \(\mathcal {M}\). If the term t is closed (i.e., if \(t\in {\mathcal {T}}_{\varSigma }\)) its interpretation is independent from g, and so we will simply write \(t^{\mathcal {M}}\) omitting the assignment.
If not otherwise specified, we will indicate with W and D the set of worlds and the domain of the model under consideration respectively.
Definition 4
Given an information model \(\mathcal {M}\) as above, we call a set \(s \subseteq W\) an information state.
Information models are used to represent pieces of information. In this context, we use the term piece of information to refer to any property I of first-order models in the given signature. For example \(I_1\): “the interpretation of c is in the extension of P” and \(I_2\): “the cardinality of the domain is finite and even” are considered pieces of information. Given a model \(\mathcal {M}\) we can encode a piece of information I with the info state \(s_I \,\,{:}{=}\,\, \{w\in W \,|\, M_w \text { has property } I \}\); that is, by selecting the worlds corresponding to the first-order models having property I. So in the examples given above, \(s_{I_1}\) consists of all the worlds \(w \in W\) for which \(M_w\) satisfies P(c); and \(s_{I_2}\) is either W or \(\emptyset \), depending on the cardinality of D.
We are now ready to present the semantics of  .
.
Definition 5
(Semantics of  ) Let
\(\mathcal {M}\) be an information model, s an information state of
\(\mathcal {M}\) and
\(g: {{\,\mathrm{\mathrm {\mathbf {Var}}}\,}}\rightarrow D\) an assignment. We define the support relation
\(\vDash \) over formulas of
) Let
\(\mathcal {M}\) be an information model, s an information state of
\(\mathcal {M}\) and
\(g: {{\,\mathrm{\mathrm {\mathbf {Var}}}\,}}\rightarrow D\) an assignment. We define the support relation
\(\vDash \) over formulas of
 by the following inductive clauses:
by the following inductive clauses:

If \(\mathcal {M}, s \vDash _g \varphi \) we say that s supports \(\varphi \) under g. We introduce the shorthand \(\mathcal {M}\vDash _g \varphi \) for \(\mathcal {M}, W \vDash _g \varphi \). It can be verified that, if \(\varphi \) is a sentence, then its semantics is independent from the assignment g. In this case we will simply omit g.
In what follows, we will give a brief introduction to the support semantics, focusing on the results instrumental for the rest of the paper. For a thorough description of the support semantics, we point to Ciardelli (2016, Ch. 4). We start by stating one of the main properties of this semantics.
Lemma 1
(Downward closure and empty state property) Let \(\varphi \) be a formula, \(s,s'\) information states of \(\mathcal {M}\) and \(g : D \rightarrow {{\,\mathrm{\mathrm {\mathbf {Var}}}\,}}\) an assignment. Then:
-
If \(\mathcal {M}, s \vDash _g \varphi \) and \(s' \subseteq s\) then \(\mathcal {M}, s' \vDash _g \varphi \);
-
\(\mathcal {M}, \emptyset \vDash _g \varphi \).
These two properties have an intuitive interpretation, in line with the one presented for information models: if a certain piece of information supports a sentence (\(\mathcal {M}, s \vDash _g \varphi \)), then any more specific information supports the same sentence too (if \(s' \subseteq s\) then \(\mathcal {M}, s' \vDash _g \varphi \)); and an inconsistent piece of information supports everything (\(\mathcal {M}, \emptyset \vDash _g \varphi \)).
Using Lemma 1, we can also easily derive a semantic clause for the operator \(\lnot \):
As usual, we associate to the semantics just introduced the corresponding concepts of validity and entailment.
Definition 6
(Validity and entailment) We say that a formula \(\varphi \) is (semantically) valid in  , and indicate it with \(\vDash \varphi \), iff for every model \(\mathcal {M}\), every information state s of \(\mathcal {M}\) and every assignment \(g: {{\,\mathrm{\mathrm {\mathbf {Var}}}\,}}\rightarrow D\), it holds \(\mathcal {M}, s \vDash _g \varphi \).
, and indicate it with \(\vDash \varphi \), iff for every model \(\mathcal {M}\), every information state s of \(\mathcal {M}\) and every assignment \(g: {{\,\mathrm{\mathrm {\mathbf {Var}}}\,}}\rightarrow D\), it holds \(\mathcal {M}, s \vDash _g \varphi \).
Given a set of formulas \(\varPhi \cup \{ \psi \}\), we say that \(\varPhi \) entail \(\psi \), and indicate it with \(\varPhi \vDash \psi \), iff for every \(\mathcal {M}\), s and g as above, if \(\mathcal {M}, s \vDash _g \varphi \) for every \(\varphi \in \varPhi \), then \(\mathcal {M}, s \vDash _g \psi \).
As an example, consider the formulas  and \(P(c) \vee \lnot P(c)\). Unraveling the semantic clauses, we obtain the following support conditions for the two formulas.
and \(P(c) \vee \lnot P(c)\). Unraveling the semantic clauses, we obtain the following support conditions for the two formulas.

It is clear that the second condition is always true, since in every world the extension of P is determined: that is, \(P(c) \vee \lnot P(c)\) is valid in  . However, the first condition is not tautological: It requires all worlds in \(\mathcal {M}\) to agree on whether c is in the extension of P.
. However, the first condition is not tautological: It requires all worlds in \(\mathcal {M}\) to agree on whether c is in the extension of P.
We observe a similar situation with the formulas  and \(\exists x. P(x)\), for which the support conditions can be derived with a similar proof.
and \(\exists x. P(x)\), for which the support conditions can be derived with a similar proof.

In this case, \(\exists x. P(x)\) requires that in every world there is an element with property P—possibly depending on the world; while the formula  asks more, namely that for a fixed element d, all the worlds agree on d being in the extension of P. So the additional requirement is that we have a witness for the quantifier which all the worlds agree on.
asks more, namely that for a fixed element d, all the worlds agree on d being in the extension of P. So the additional requirement is that we have a witness for the quantifier which all the worlds agree on.
The differences between the operators  \(\vee \), and between the operators
\(\vee \), and between the operators  and \(\exists \) are also witnessed by two peculiar properties of the support semantics: the disjunction and existence properties for the inquisitive operators.
and \(\exists \) are also witnessed by two peculiar properties of the support semantics: the disjunction and existence properties for the inquisitive operators.
Theorem 7
(Theorems 4.1 and 4.2 in Grilletti (2019)) Fix a signature \(\varSigma \). Given a set of classical formulas \(\varGamma \), for every formulas \(\varphi \) and \(\psi \) we have:
-
If
 , then \(\varGamma \vDash \varphi \) or \(\varGamma \vDash \psi \);
, then \(\varGamma \vDash \varphi \) or \(\varGamma \vDash \psi \); -
If
 , then \(\varGamma \vDash \varphi [t/x]\) for some term t of \(\varSigma \).
, then \(\varGamma \vDash \varphi [t/x]\) for some term t of \(\varSigma \).
In particular, this highlights the constructive character of the inquisitive operators 
 , in contrast with the operators \(\vee \) and \(\exists \) which behave classically.
, in contrast with the operators \(\vee \) and \(\exists \) which behave classically.
However, if we restrict our attention to singleton information states, that is, information states containing only one world, we can see that the support semantics is a generalization of the usual semantics of first order classical logic. In this case the support condition for  \(\vee \) coincide, the support condition for \(\exists \) and
\(\vee \) coincide, the support condition for \(\exists \) and  also coincide, and so a formula \(\varphi \) is supported in a state \(\{w\}\) if and only if its classical variant \(\varphi ^{cl}\)—obtained by substituting \(\vee \) for
also coincide, and so a formula \(\varphi \) is supported in a state \(\{w\}\) if and only if its classical variant \(\varphi ^{cl}\)—obtained by substituting \(\vee \) for  \(\exists \) for
\(\exists \) for  in \(\varphi \)—is true in \(M_w\).
in \(\varphi \)—is true in \(M_w\).
The following result generalizes the previous observation and connects classical semantics and support semantics. We will indicate with \(\vDash ^{cl}\) both the standard semantics relation of classical first order logic and the corresponding entailment relation between classical formulas.
Lemma 8
Let \(\alpha \) be a classical formula. Then
In particular, a classical formula is valid for support semantics iff it is valid for the classical semantics; and the entailment relations \(\vDash \) and \(\vDash ^{cl}\) coincide over classical formulas.
With a slight abuse of notation (justified by the lemma), henceforth we will use the symbol \(\vDash \) both for support semantics (resp., entailment) and for the standard semantics (resp., entailment) of classical first order logic, omitting the superscript cl.
This result has rather interesting consequences and will be used several times in the current manuscript. For example we have the following: given a classical formula \(\alpha \), a model \(\mathcal {M}\) and an assignment g, there is always a greatest information state satisfying \(\alpha \), namely the set \(|\alpha | \,\,{:}{=}\,\, \{ w \in W \;|\; M_w \vDash ^{cl}_g \alpha \}\); and given an information state s, the state \(s \cap |\alpha |\) is the greatest substate of s supporting \(\alpha \).
Lemma 8 is particularly interesting under the information-based interpretation: given an information state s, a certain statement—encoded by \(\alpha \)—is supported by s if and only if in every possible world in s the statement is true. Moreover, under this interpretation \(|\alpha |\) represents exactly the information conveyed by the statement encoded by \(\alpha \).
Similarly, we can also talk about support for questions: a question is supported by an information state s iff s resolves the issue raised by the question. So for example  , representing the alternative question “Will Joey come to the party or not?”, is supported by s iff in all the possible worlds Joey will go to the party or in all the possible worlds Joey will not go to the party; that is, the information encoded by s must be enough to determine an answer to the question. For an exhaustive treatment of the conceptual background of the logic we refer to Ciardelli (2016, Chs. 1, 2 and 4).
, representing the alternative question “Will Joey come to the party or not?”, is supported by s iff in all the possible worlds Joey will go to the party or in all the possible worlds Joey will not go to the party; that is, the information encoded by s must be enough to determine an answer to the question. For an exhaustive treatment of the conceptual background of the logic we refer to Ciardelli (2016, Chs. 1, 2 and 4).
We conclude this section by presenting a sound natural deduction system for  and some related concepts.
and some related concepts.
Definition 9
(Natural deduction system) Consider the natural deduction system in Table 1. We say that a set of formulas \(\varPhi \) derives a formula \(\psi \) (in symbols  ) if there is a derivation of \(\psi \) from \(\varPhi \) in the natural deduction system.
) if there is a derivation of \(\psi \) from \(\varPhi \) in the natural deduction system.

This system was presented in Ciardelli (2016, Ch. 4). It is still an open question if the system is complete for  . What is known Ciardelli (2016, Proposition 4.4.3) is that this system is complete for classical consequences. Given a set of formulas \(\varPhi \), define \(\varPhi ^{cl} \,\,{:}{=}\,\, \{ \varphi ^{cl} \;|\; \varphi \in \varPhi \}\). We will indicate with
. What is known Ciardelli (2016, Proposition 4.4.3) is that this system is complete for classical consequences. Given a set of formulas \(\varPhi \), define \(\varPhi ^{cl} \,\,{:}{=}\,\, \{ \varphi ^{cl} \;|\; \varphi \in \varPhi \}\). We will indicate with  the standard provability relation of classical first order logic.
the standard provability relation of classical first order logic.
Lemma 10
Let \(\varPhi \) be a set of inquisitive formulas and \(\alpha \) a classical formula. Then

In particular,  coincides with the usual classical entailment when \(\varPhi \) consists only of classical formulas; and a classical formula is valid in
coincides with the usual classical entailment when \(\varPhi \) consists only of classical formulas; and a classical formula is valid in  if and only if it is valid in classical first order logic.
if and only if it is valid in classical first order logic.
With slight abuse of notation (justified by the lemma), we will indicate with  both the provability relation from Definition 9 and the standard provability relation of classical first order logic, omitting the superscript cl.
both the provability relation from Definition 9 and the standard provability relation of classical first order logic, omitting the superscript cl.
It is worth discussing two rules of this system, which play an essential role in the rest of the paper:  -split rule and the
-split rule and the  -split rule. Notice that these rules are natural counterparts of the disjunction and existence properties of the support semantics. Moreover, these rules have a natural reading under the information-based interpretation: if a statement resolves an alternative question (
-split rule. Notice that these rules are natural counterparts of the disjunction and existence properties of the support semantics. Moreover, these rules have a natural reading under the information-based interpretation: if a statement resolves an alternative question ( ), then it supports one of the alternatives (
), then it supports one of the alternatives ( ); and if a statement resolves a witness question (
); and if a statement resolves a witness question ( ), then it provides enough information to pinpoint a witness (
), then it provides enough information to pinpoint a witness ( ).
).
The proofs of soundness of the rules follow this same intuition. Let us show the case  -split as an example:
-split as an example:

Finally, notice that the rules are not sound without the restriction on the antecedent \(\alpha \) being classical. For example, consider the formula

which is trivially valid. If we could apply the rule to this formula, by the disjunction property (Theorem 7) we would have that  would be valid or
would be valid or  would be valid. But this is clearly not the case, as it is easy to produce counterexamples for both formulas.
would be valid. But this is clearly not the case, as it is easy to produce counterexamples for both formulas.
3 ClAnt Fragment
In this section we present the main protagonist of this paper, that is, the \(\mathsf {ClAnt}\) fragment.
Definition 11
(\(\mathsf {ClAnt}\) fragment) The \(\mathsf {ClAnt}\) fragment is generated by the following grammar:

where \(\alpha \) ranges over classical formulas.
In Ciardelli (2016, Ch. 4), two other fragments were presented and studied, namely the mention-some ( ) and the mention-all fragment (\({\mathcal {L}}_{\forall }\)). These two fragments are generated by the following grammars:
) and the mention-all fragment (\({\mathcal {L}}_{\forall }\)). These two fragments are generated by the following grammars:

where \(\alpha \) ranges over classical formulas.
It was proven in Ciardelli (2016) that the support relation for inquisitive logic restricted to both these fragments is axiomatizable. Interestingly, the proofs presented are quite different and cannot, prima facie, be adapted to the other fragment. For the mention-some fragment, the completeness proof uses a canonical model construction similar to the one proposed for propositional inquisitive logic in Ciardelli (2016, Ch. 3), heavily relying on the existence of a disjunctive normal form for formulas. For the mention-all fragment, the completeness proof passes through a translation in the Logic of Interrogation (Groenendijk 1999; ten Cate and Shan 2007), a logic with a partition-based semantics.
Notice that \(\mathsf {ClAnt}\) subsumes both these fragments. So the axiomatization for \(\mathsf {ClAnt}\) and the corresponding completeness proof, presented in Sects. 4 and 5 respectively, introduce a novel approach to axiomatize both  and \({\mathcal {L}}_{\forall }\). Moreover, \(\mathsf {ClAnt}\) is strictly more expressive than both these fragments, as shown by the following result.
and \({\mathcal {L}}_{\forall }\). Moreover, \(\mathsf {ClAnt}\) is strictly more expressive than both these fragments, as shown by the following result.
Proposition 12
The sentence  is in \(\mathsf {ClAnt}\) and it is not logically equivalent to any formula in
is in \(\mathsf {ClAnt}\) and it is not logically equivalent to any formula in  in the same signature.
in the same signature.
This formula holds if for every element x there is an associated element y such that exactly one of them has property P. This condition is particularly interesting in contexts where epistemic identity does not correspond to ontological identity, like inquisitive logic (see Ciardelli 2016, Sec. 4.3.4 for a small discussion on the topic).
The models used in the proof of Proposition 12
Proof
In the scope of this proof, we will use the notation  . \(\theta \) is clearly in \(\mathsf {ClAnt}\)—notice that \(P(x) \leftrightarrow \lnot P(y)\) is a classical formula.
. \(\theta \) is clearly in \(\mathsf {ClAnt}\)—notice that \(P(x) \leftrightarrow \lnot P(y)\) is a classical formula.
To show that \(\theta \) is not equivalent to a formula in  , consider the models depicted in Fig. 1a. It is straightforward to verify that \(\mathcal {M} \vDash \theta \), while \(\mathcal {N} \nvDash \theta \). Assume towards a contradiction that \(\theta \) is equivalent to a formula in
, consider the models depicted in Fig. 1a. It is straightforward to verify that \(\mathcal {M} \vDash \theta \), while \(\mathcal {N} \nvDash \theta \). Assume towards a contradiction that \(\theta \) is equivalent to a formula in  . By the normal form described in Ciardelli (2016, Proposition 4.7.2), this means that
. By the normal form described in Ciardelli (2016, Proposition 4.7.2), this means that

for some \(\alpha _1, \dots , \alpha _n\) classical formulas. In particular, this means that for some \(i \in \{ 1,\dots ,n\}\) we have  , that is, \(\mathcal {M} \vDash _{g} \alpha _i\) for some assignment g.
, that is, \(\mathcal {M} \vDash _{g} \alpha _i\) for some assignment g.
Notice that the only atomic formulas available in the current language are \(\bot \) and P(x) for x a variable. So if \(g(x) = b\), the assignments g and \(g[x\mapsto a]\) satisfy exactly the same atomic formulas, and consequently the same complex formulas. And the same applies for g and the assignment h defined as follows:
Since the image of h is contained in \(\{a,c\}\) and \(\mathcal {M} \vDash _h \alpha _i\), with a similar reasoning we also obtain that \(\mathcal {N}, \{w\} \vDash _h \alpha _i\) and \(\mathcal {N}, \{v\} \vDash _h \alpha _i\). Thus by Lemma 8 we have \(\mathcal {N} \vDash _h \alpha _i\) and consequently \(\mathcal {N} \vDash \theta \). And this is a contradiction, as wanted.
To show that \(\theta \) is not equivalent to a formula in \({\mathcal {L}}_{\forall }\) we use Ciardelli (2016, Proposition 4.8.4), which states that every formula \(\varphi \in {\mathcal {L}}_{\forall }\) is pair-distributive, that is:
So we just need to show that \(\theta \) is not pair-distributive: given the model in Fig. 1b, every state \(s'\) with at most two worlds satisfies \(\theta \), but the whole model does not. \(\square \)
We conclude this section with an alternative presentation of the \(\mathsf {ClAnt}\) fragment.
Lemma 13
Every formula in \(\mathsf {ClAnt}\) is equivalent to a formula generated by the following grammar:

where \(\alpha \) ranges over classical formulas.
Proof
(Sketch) The main idea of the proof is to “massage” the implications toward the classical formulas using the following equivalences, taking care of renaming the bounded variables when necessary.

Notice that the equivalences read from left to right reduce the complexity of the consequent of the implication. Consequently, after enough reduction steps all the implications appear in subformulas of the form \(\alpha \rightarrow \beta \), which are themselves classical formulas. \(\square \)
This result tells us that we can dispense with implications outside of classical formulas. At the level of expressive power this is a significant limitation, since \(\rightarrow \) is the only logical operator acting as a second-order quantifier for the semantics—compare with Definition 5. It is not clear yet whether the completeness proof presented in the following sections relies on this limitation or can be generalized to more expressive fragments, or even the whole logic. What is known, is that \(\mathsf {ClAnt}\) is strictly less expressive than  , as the following result shows.
, as the following result shows.
Claim
The formula \(\forall x. ?P(x) \rightarrow ?r\) (for P a unary relation symbol and r a 0-ary relation symbol) is not logically equivalent to any formula in \(\mathsf {ClAnt}\).
The only proof known to the author of this result relies on Lemma 13, but uses also a variation of the Ehrenfeucht-Fraïssé game for  introduced in Gianluca and Ivano (2019), which has not yet been discussed in the literature. Since presenting and discussing these results strides away from the intended objective of this paper, we leave the claim unproven for now, with the promise to present the proof in future works.
introduced in Gianluca and Ivano (2019), which has not yet been discussed in the literature. Since presenting and discussing these results strides away from the intended objective of this paper, we leave the claim unproven for now, with the promise to present the proof in future works.
4 Deductive System
Definition 14
(Natural deduction system for \(\mathsf {ClAnt}\)) For \(\varPhi \cup \{ \psi \}\) \(\mathsf {ClAnt}\) formulas we say that \(\varPhi \) derives \(\psi \) in \(\mathsf {ClAnt}\) (in symbols  ) if there is a derivation of \(\psi \) from \(\varPhi \) containing only \(\mathsf {ClAnt}\) formulas.
) if there is a derivation of \(\psi \) from \(\varPhi \) containing only \(\mathsf {ClAnt}\) formulas.
Clearly if  then
then  , but a priori nothing ensures that if there exists a derivation of \(\psi \) from \(\varPhi \), then there exists also a derivation containing only \(\mathsf {ClAnt}\) formulas. However, we will show in Theorem 34 that this is indeed the case.
, but a priori nothing ensures that if there exists a derivation of \(\psi \) from \(\varPhi \), then there exists also a derivation containing only \(\mathsf {ClAnt}\) formulas. However, we will show in Theorem 34 that this is indeed the case.
Notice that if we apply a rule in Table 1 to \(\mathsf {ClAnt}\) formulas, the conclusion produced is again a \(\mathsf {ClAnt}\) formula, the only exception being \((\rightarrow i)\). In particular, the conclusion of \((\rightarrow i)\) is a \(\mathsf {ClAnt}\) formula iff the discharged assumption is a classical formula, that is, if the rule is applied with the following side condition:

From this observation, it follows that  can be characterized as the provability relation of the natural deduction system obtained by replacing the rule (\(\rightarrow \)i) with the rule (\(\mathsf {ClAnt}\rightarrow \)i) in Table 1.
can be characterized as the provability relation of the natural deduction system obtained by replacing the rule (\(\rightarrow \)i) with the rule (\(\mathsf {ClAnt}\rightarrow \)i) in Table 1.
To study the properties of this system and the relations with the system presented in Definition 9, we focus on theories of  and of \({\mathsf {ClAnt}}\), that is, sets of formulas in
and of \({\mathsf {ClAnt}}\), that is, sets of formulas in  and in \(\mathsf {ClAnt}\) respectively. Since we need to be particularly careful when handling free variables, we distinguish between sets of formulas and theories.
and in \(\mathsf {ClAnt}\) respectively. Since we need to be particularly careful when handling free variables, we distinguish between sets of formulas and theories.
Definition 15
Let \(\varSigma \) be a fixed signature.
-
A set of \(\varSigma \)-formulas is any set \(\varPhi \) of
 formulas in the signature \(\varSigma \).
formulas in the signature \(\varSigma \). -
A \(\varSigma \)-theory is any set \(\varPhi \) of
 sentences in the signature \(\varSigma \).
sentences in the signature \(\varSigma \).
So \(\varSigma \)-theories do not contain formulas with free variables, while sets of \(\varSigma \)-formulas may. It is easy to transform a set of \(\varSigma \)-formulas in a corresponding theory, at the cost of adding new constant symbols to the signature. For A a set of parameters—that we assume disjoint from the set \(\varSigma \)—we define \(\varSigma (A)\) as the signature extending \(\varSigma \) with the elements of A as fresh constant symbols.
Definition 16
Let \(\varPhi \) be a set of \(\varSigma \)-formulas and let V be the set of free variables appearing in \(\varPhi \). Consider a set \({\widetilde{V}} \,\,{:}{=}\,\, \{\, {\widetilde{x}} \,|\, x\in V \,\}\) of distinct formal parameters. We define the closure of \(\varPhi \) as the \(\varSigma ({\widetilde{V}})\)-theory \({\widetilde{\varPhi }}\) obtained by substituting every free occurrence of the variable x in \(\varPhi \) with \({\widetilde{x}}\), for every \(x\in V\).
Proposition 17
Let \(\varPhi \cup \{\psi \}\) be a set of \(\varSigma \)-formulas. ThenFootnote 4
The proof consists only in comparing the semantic clauses of the two entailments, and it is therefore omitted. This proposition allows us to focus our attention on theories and to highlight the role of the parameters in the proofs that follow.
To prove the completeness of the system introduced, we need to study more in detail three special classes of theories: saturated theories, classically saturated theories and \(\mathsf {ClAnt}\)-saturated theories. In what follows, we will indicate with A a fixed set of constant symbols not appearing in the signature \(\varSigma \).
Definition 18
(Saturated theory) A \(\varSigma (A)\)-theory \(\varPhi \) is called saturated (with respect to A) if for every sentences \(\varphi ,\psi \) of \(\varSigma (A)\) it satisfies:

It is easy to produce examples of saturated theories: Consider an inquisitive model \(\mathcal {M}\) on the signature \(\varSigma (A)\) for which the interpretations of the terms in \({\mathcal {T}}_{\varSigma (A)}\) cover the whole domain, that is, \(\{ t^{\mathcal {M}} \;|\; t\in {\mathcal {T}}_{\varSigma (A)} \} = D\)—henceforth we will call these models \({\mathcal {T}}_{\varSigma (A)}\)-covered. Given an information state s, define the theory of \(\left\langle \mathcal {M},s \right\rangle \) as \(\mathrm {Th}(\mathcal {M},s) = \{\, \varphi \text { sentence of } \varSigma (A) \,|\, \mathcal {M}, s \vDash \varphi \,\}\). It is immediate to show that \(\mathrm {Th}(\mathcal {M},s)\) is a saturated \(\varSigma (A)\)-theory. In particular, the existence property and the normality condition rely on the fact that the model is \({\mathcal {T}}_{\varSigma (A)}\)-covered.
If we restrict our attention only to classical formulas, we can define the corresponding concept of classically-saturated theory.
Definition 19
(Classical theories and classically saturated theories) A classical \(\varSigma \)-theory is a \(\varSigma \)-theory containing only classical formulas.
We say that a classical \(\varSigma (A)\)-theory \(\varGamma \) is classically-saturated (with respect to A) if for every classical sentences \(\alpha ,\beta \) of \(\varSigma (A)\) it satisfies:

A simple induction shows that, given \(\varGamma \cup \{ \alpha \}\) classical formulas,  if and only if \(\alpha \) is a consequence of \(\varGamma \) in classical first order logic. This observation, in conjunction with deductive closure and the disjunction property, tells us that a classically-saturated theory \(\varGamma \) is complete, that is, for every sentence \(\alpha \) of \(\varSigma (A)\) we have either \(\alpha \in \varGamma \) or \(\lnot \alpha \in \varGamma \). And in turns, it follows that the condition corresponding to normality is also satisfied:
if and only if \(\alpha \) is a consequence of \(\varGamma \) in classical first order logic. This observation, in conjunction with deductive closure and the disjunction property, tells us that a classically-saturated theory \(\varGamma \) is complete, that is, for every sentence \(\alpha \) of \(\varSigma (A)\) we have either \(\alpha \in \varGamma \) or \(\lnot \alpha \in \varGamma \). And in turns, it follows that the condition corresponding to normality is also satisfied:

Classically-saturated theories are examples of Hintikka sets for classical first order logic (see for example Hodges 1993, Sec. 2.3). This is particularly relevant, since every Hintikka set \(\varGamma \) admits a first-order model \(M_\varGamma \), and it is thus satisfiable.
We will sketch the construction of \(M_\varGamma \) for \(\varGamma \) a classically-saturated \(\varSigma (A)\)-theory, essentially following the proof of Theorem 2.3.3 in Hodges (1993).
Definition 20
Given \(\varGamma \) a classically-saturated \(\varSigma (A)\)-theory, we define the model \(M_\varGamma \) by the following clauses:
-
The domain of \(M_\varGamma \) is the set \({\mathcal {T}}_{\varSigma (A)}\);
-
A constant symbol \(c \in \varSigma \) is interpreted as itself, that is, \(c^{M_\varGamma } = c\). The same applies for a parameter \(a \in A\): \(a^{M_\varGamma } = a\).
-
An n-ary function symbol f different from a constant is interpreted as the corresponding term combinator, that is:
$$\begin{aligned} \begin{array}{l c @{} l @{} c} f^{M_\varGamma }: &{}({\mathcal {T}}_{\varSigma (A)})^n &{}\rightarrow &{}{\mathcal {T}}_{\varSigma (A)} \\ &{} \left\langle t_1, \dots , t_n \right\rangle &{}\mapsto &{}f(t_1, \dots , t_n) \end{array} \end{aligned}$$ -
An n-ary relation symbol R is interpreted as the relation defined by the following clause:
$$\begin{aligned} R^{M_\varGamma }(t_1,\dots ,t_n) \qquad \text {iff}\qquad R(t_1,\dots ,t_n) \in \varGamma \end{aligned}$$
Notice that by construction the model \(M_\varGamma \) is \({\mathcal {T}}_{\varSigma (A)}\)-covered. Another peculiar property of \(M_\varGamma \) is that it satisfies exactly the sentences in \(\varGamma \), that is:
Lemma 21
(Truth Lemma) For every classical sentence \(\alpha \) of \(\varSigma (A)\) we have
The proof of this result (which we omit) consists of a simple structural induction on \(\alpha \). As an example, we sketch the inductive step for the case \(\alpha \) of the form \(\exists x. \beta \).
It is useful to interpret these results on classically-saturated theories also in terms of support semantics. To do this, we firstly introduce the concept of classical part of a theory—and for later use, also the concept of \(\mathsf {ClAnt}\) part of a theory.
Definition 22
(Classical part and \(\mathsf {ClAnt}\) part of \(\varPhi \)) Let \(\varPhi \) be a theory. The classical part of \(\varPhi \) ( ) and the \(\mathsf {ClAnt}\) part of \(\varPhi \) (
) and the \(\mathsf {ClAnt}\) part of \(\varPhi \) ( ), are defined as the set of classical formulas contained in \(\varPhi \) and the set of \(\mathsf {ClAnt}\) formulas contained in \(\varPhi \) respectively.
), are defined as the set of classical formulas contained in \(\varPhi \) and the set of \(\mathsf {ClAnt}\) formulas contained in \(\varPhi \) respectively.
Corollary 23
The followings hold:
-
Let \(\mathcal {M}\) be a \({\mathcal {T}}_{\varSigma (A)}\)-covered model on the signature \(\varSigma (A)\) and w a world of \(\mathcal {M}\). Then
 is a classically-saturated \(\varSigma (A)\)-theory.
is a classically-saturated \(\varSigma (A)\)-theory. -
Let \(\varGamma \) be a classically-saturated \(\varSigma (A)\)-theory. Then there exists a model \(\mathcal {M}\) on the signature \(\varSigma (A)\) and a world w of \(\mathcal {M}\) such that
 .
.
If we restrict our attention to \({\mathcal {T}}_{\varSigma (A)}\)-covered models in the signature \(\varSigma (A)\), Corollary 23 tells us that classically saturated theories are exactly the classical parts of theories of singleton information states, that is, states of the form \(\{w\}\).
It is worth noticing that for an arbitrary information state s, the set  is not necessarily classically-saturated. Take for example an enhanced version of the information model \(\mathcal {N}\) from Fig. 1a, obtained by
is not necessarily classically-saturated. Take for example an enhanced version of the information model \(\mathcal {N}\) from Fig. 1a, obtained by
-
extending the signature of \(\mathcal {N}\) with the set of parameters A;
-
interpreting the elements of A so as to cover the whole domain \(\{ a, b, c \}\).
Let us call this enhanced model \(\mathcal {N}\,'\) and fix \(s \,\,{:}{=}\,\, \{w,v\}\). Since \(\mathcal {N}\,', s \nvDash P(b)\) and \(\mathcal {N}\,', s \nvDash \lnot P(b)\), we have that  is not complete—independently from the in terpretation of the new parameters—and consequently
is not complete—independently from the in terpretation of the new parameters—and consequently  does not satisfy the Classical disjunction property.
does not satisfy the Classical disjunction property.
Finally, we restrict our attention only to \(\mathsf {ClAnt}\) formulas, obtaining the concept of \(\mathsf {ClAnt}\)-saturated theory.
Definition 24
(\(\mathsf {ClAnt}\)-theories and \(\mathsf {ClAnt}\)-saturated theories) A \(\mathsf {ClAnt}\) \(\varSigma \)-theory is a \(\varSigma \)-theory containing only \(\mathsf {ClAnt}\) formulas.
We say that a \(\mathsf {ClAnt}\) \(\varSigma (A)\)-theory \(\varPhi \) is \(\mathsf {ClAnt}\)-saturated (with respect to A) if for every \(\mathsf {ClAnt}\) sentences \(\varphi ,\psi \) of \(\varSigma (A)\) it satisfies:

From Definition 14 it follows readily that, given \(\varPhi \) a saturated \(\varSigma (A)\)-theory, the subset of its \(\mathsf {ClAnt}\) formulas is a \(\mathsf {ClAnt}\)-saturated \(\varSigma (A)\)-theory. The converse—that every \(\mathsf {ClAnt}\)-saturated theory can be obtained by restricting a saturated theory in the whole language—is not as obvious, but surprisingly it is the case.
Theorem 25
Let \(\varPhi \) be a \(\mathsf {ClAnt}\)-saturated \(\varSigma (A)\)-theory. Then there exists a saturated \(\varSigma (A)\)-theory \(\varPsi \) such that  .
.
The rest of this section is dedicated to proving this result. Henceforth, given a \(\mathsf {ClAnt}\)-theory \(\varPhi \), we will indicate with \(\overline{\varPhi }\) its deductive closure with respect to  —which is again a \(\mathsf {ClAnt}\)-theory.
—which is again a \(\mathsf {ClAnt}\)-theory.
Lemma 26
Given \(\varPhi \) a \(\mathsf {ClAnt}\)-saturated \(\varSigma (A)\)-theory and \(\alpha \) a classical sentence such that  , then \(\overline{\varPhi \cup \{\alpha \}}\) is \(\mathsf {ClAnt}\)-saturated \(\varSigma (A)\)-theory.
, then \(\overline{\varPhi \cup \{\alpha \}}\) is \(\mathsf {ClAnt}\)-saturated \(\varSigma (A)\)-theory.
Proof
Let us call \(\varTheta \,\,{:}{=}\,\, \overline{\varPhi \cup \{\alpha \}}\). Clearly \(\varTheta \) is deductively closed. Moreover it is coherent, since  iff
iff  :
:
the left-to-right implication can be deduced using the rule \((\mathsf {ClAnt}\rightarrow i)\); the right-to-left implication can be deduced using the rule \((\rightarrow e)\).
So we just need to show that \(\varTheta \) satisfies the disjunction property, the existence property and the normality condition.
Disjunction property

Existence property
Notice that since \(\alpha \) is a sentence, x does not appear free in \(\alpha \).

Normality condition
Notice that since \(\alpha \) is a sentence and \(\varTheta \) is a theory, x and y do not appear free in \(\alpha \) nor \(\varTheta \).

\(\square \)
Lemma 27
Let \(\varPhi , \varPsi \) be two \(\mathsf {ClAnt}\)-saturated \(\varSigma (A)\)-theories such that  . Then \(\varPhi = \varPsi \).
. Then \(\varPhi = \varPsi \).
Proof
We start with a sub-lemma: given any \(\varPhi \) and \(\varPsi \) as in the hypothesis, then for every classical formula \(\alpha \) it holds  . The proof is straightforward:
. The proof is straightforward:
Using this technical result, we can show by induction on the length of the \(\mathsf {ClAnt}\) sentence \(\theta \)—intended as the number of symbols appearing in \(\theta \)—that \(\theta \in \varPhi \iff \theta \in \varPsi \).
-
If \(\theta \) is an atom, the result follows by hypothesis—atoms are classical formulas.
-
If \(\theta \equiv \psi \wedge \chi \), then
$$\begin{aligned}&\theta \in \varPhi \\ \iff&\psi \in \varPhi \text { and } \chi \in \varPhi&\text {Deductive closure of } \varPhi \\ \iff&\psi \in \varPsi \text { and } \chi \in \varPsi&\text {Inductive hypothesis} \\ \iff&\theta \in \varPsi&\text {Deductive closure of } \varPsi \end{aligned}$$ -
If
 , then $$\begin{aligned}&\theta \in \varPhi \\ \iff&\psi \in \varPhi \text { or } \chi \in \varPhi&\text {Deductive closure and Disjunction property of } \varPhi \\ \iff&\psi \in \varPsi \text { or } \chi \in \varPsi&\text {Inductive hypothesis} \\ \iff&\theta \in \varPsi&\text {Deductive closure and Disjunction property of } \varPsi \end{aligned}$$
, then $$\begin{aligned}&\theta \in \varPhi \\ \iff&\psi \in \varPhi \text { or } \chi \in \varPhi&\text {Deductive closure and Disjunction property of } \varPhi \\ \iff&\psi \in \varPsi \text { or } \chi \in \varPsi&\text {Inductive hypothesis} \\ \iff&\theta \in \varPsi&\text {Deductive closure and Disjunction property of } \varPsi \end{aligned}$$ -
If \(\theta \equiv \alpha \rightarrow \psi \), then
$$\begin{aligned}&\theta \in \varPhi \\ \iff&\psi \in \overline{\varPhi \cup \{\alpha \}}&(\mathsf {ClAnt}\rightarrow i) \text { and } (\rightarrow e) \\ \iff&\psi \in \overline{\varPsi \cup \{\alpha \}}&\text {Inductive hypothesis applied to } \overline{\varPhi \cup \{\alpha \}} \text { and } \overline{\varPsi \cup \{\alpha \}} \\ \iff&\theta \in \varPsi&(\mathsf {ClAnt}\rightarrow i) \text { and } (\rightarrow e) \end{aligned}$$Notice that we can apply the inductive hypothesis to the theories \(\overline{\varPhi \cup \{\alpha \}}\) and \(\overline{\varPsi \cup \{\alpha \}}\) since by Lemma 26 they are \(\mathsf {ClAnt}\)-saturated theories, and we showed at the beginning of the proof that
 .
. -
If
 , then $$\begin{aligned}&\theta \in \varPhi \\ \iff&\psi [t/x] \in \varPhi \quad \text {for some } t \in {\mathcal {T}}_{\varSigma (A)}&\text {Existence property for } \varPhi \\ \iff&\psi [t/x] \in \varPsi \quad \text {for some } t \in {\mathcal {T}}_{\varSigma (A)}&\text {Inductive hypothesis} \\ \iff&\theta \in \varPsi&\text {Existence property for } \varPsi \end{aligned}$$
, then $$\begin{aligned}&\theta \in \varPhi \\ \iff&\psi [t/x] \in \varPhi \quad \text {for some } t \in {\mathcal {T}}_{\varSigma (A)}&\text {Existence property for } \varPhi \\ \iff&\psi [t/x] \in \varPsi \quad \text {for some } t \in {\mathcal {T}}_{\varSigma (A)}&\text {Inductive hypothesis} \\ \iff&\theta \in \varPsi&\text {Existence property for } \varPsi \end{aligned}$$ -
If \(\theta \equiv \forall x.\psi \), then
$$\begin{aligned}&\theta \in \varPhi \\ \iff&\varphi [t/x] \in \varPhi \quad \text {for all } t \in {\mathcal {T}}_{\varSigma (A)}&\text {Normality condition for } \varPhi \\ \iff&\psi [t/x] \in \varPsi \quad \text {for all } t \in {\mathcal {T}}_{\varSigma (A)}&\text {Inductive hypothesis} \\ \iff&\theta \in \varPsi&\text {Normality condition for } \varPsi \end{aligned}$$
\(\square \)
To obtain a result analogous to Corollary 23, we need to introduce a construction resembling the canonical models for intuitionistic logic.
Definition 28
(Canonical model) We define \(\mathcal {M}^c\) the canonical model of \(\varSigma (A)\) by the following clauses:
-
The set of worlds is \(W^c\), the set of classically-saturated \(\varSigma (A)\)-theories;
-
The common domain of the structures is \(D^c \,\,{:}{=}\,\, {\mathcal {T}}_{\varSigma (A)}\);
-
The model corresponding to world \(\varGamma \) is \(M_\varGamma \)—introduced in Definition 20.
As a direct consequence of Definition 28 and of Lemma 21, we have that  . From this observation we obtain the following Lemma.
. From this observation we obtain the following Lemma.
Lemma 29
Let \(s \subseteq W^c\) and \(\varGamma \) a classical theory. Then
Proof
For every \(\alpha \in \varGamma \) we have
\(\square \)
Given a coherent classical \(\varSigma (A)\)-theory \(\varTheta \) it is not generally true that there exists a world of the canonical model satisfying \(\varTheta \). A simple example, for P a unary predicate symbol, is \(\varTheta \,\,{:}{=}\,\, \{\, \lnot \forall x. P(x) \,\} \cup \{\, P(t) \,|\, t\in {\mathcal {T}}_{\varSigma (A)} \,\}\). The problem in this case is that for every theory \(\varGamma \) of a world of the canonical model—that is, by Lemma 29, for every classically-saturated \(\varSigma (A)\)-theory \(\varGamma \)—if  then there must be a witness \(t\in {\mathcal {T}}_{\varSigma (A)}\) for which
then there must be a witness \(t\in {\mathcal {T}}_{\varSigma (A)}\) for which  .
.
So the normality condition is necessary for such a world to exist. The following lemma shows that it is also a sufficient condition.Footnote 5
Lemma 30
(Classical saturation lemma) Let \(\varTheta \) be a coherent classical \(\varSigma (A)\)-theory such that for every sentence \(\alpha \) in the signature \(\varSigma (A)\) it holds:

Then there exists a classically-saturated \(\varSigma (A)\)-theory \(\varGamma \) such that \(\varTheta \subseteq \varGamma \).
Proof
This proof is an adaptation of the proof of Theorem (Gabbay 1981, Sec. 3.3, Theorem 2) for the intuitionistic case.
We start by showing a useful property, that we will later refer to as \((*)\)-property: given \(\beta \) a classical sentence of \(\varSigma (A)\), if \(\varDelta \) is a classical theory that satisfies the normality condition above then \(\varDelta \cup \{ \beta \}\) also satisfies the condition. In fact for any classical formula \(\alpha \) we have

Now we go back to the main proof. Fix an enumeration \(B_0,B_1,\dots \) of the classical sentences in the signature \(\varSigma (A)\). We will define inductively a chain of classical \(\varSigma (A)\)-theories \(\varGamma _i\) indexed by \({\mathbb {N}}\) such that:
-
1.
\(\varGamma _i\) is coherent, that is,
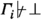 .
. -
2.
For every index i, \(\varGamma _i \subseteq \varGamma _{i+1}\).
-
3.
For every index i, \(\varGamma _i\) respects the normality condition.
The plan is to take \(\varGamma \,\,{:}{=}\,\, \cup _{i\in {\mathbb {N}}} \varGamma _i\). During the construction we will impose some additional conditions to ensure \(\varGamma \) to be a classically-saturated \(\varSigma (A)\)-theory. We start the construction by defining \(\varGamma _0 \,\,{:}{=}\,\, \varTheta \). By hypothesis conditions 1 and 3 are respected; condition 2 is trivially respected.
Suppose we already defined \(\varGamma _n\) with the properties above. We proceed by cases.
-
Case
 and \(B_n \ne \exists x. \alpha \). Define \(\varGamma _{n+1} \,\,{:}{=}\,\, \varGamma _n \cup \{ B_n \}\). Condition 1 follows from
and \(B_n \ne \exists x. \alpha \). Define \(\varGamma _{n+1} \,\,{:}{=}\,\, \varGamma _n \cup \{ B_n \}\). Condition 1 follows from  ; condition 2 is trivially satisfied; condition 3 follows from the \((*)\)-property.
; condition 2 is trivially satisfied; condition 3 follows from the \((*)\)-property. -
Case
 and \(B_n = \exists x. \alpha \). Notice that
and \(B_n = \exists x. \alpha \). Notice that  . So by condition 3 and the \((*)\)-property, there exists a term \(t\in {\mathcal {T}}_{\varSigma (A)}\) such that
. So by condition 3 and the \((*)\)-property, there exists a term \(t\in {\mathcal {T}}_{\varSigma (A)}\) such that  . Define \(\varGamma _{n+1} \,\,{:}{=}\,\, \varGamma _n \cup \{ B_n, \alpha [t/x] \}\). Condition 1 follows from
. Define \(\varGamma _{n+1} \,\,{:}{=}\,\, \varGamma _n \cup \{ B_n, \alpha [t/x] \}\). Condition 1 follows from  and
and  ; Condition 2 trivially holds; Condition 3 follows from the \((*)\)-property.
; Condition 2 trivially holds; Condition 3 follows from the \((*)\)-property. -
Case
 . Define \(\varGamma _{n+1} \,\,{:}{=}\,\, \varGamma _n\). Conditions 1,2 and 3 trivially hold.
. Define \(\varGamma _{n+1} \,\,{:}{=}\,\, \varGamma _n\). Conditions 1,2 and 3 trivially hold.
Define \(\varGamma \,\,{:}{=}\,\, \cup _{i\in {\mathbb {N}}} \varGamma _i\). By Condition 2, \(\varTheta \subseteq \varGamma \). So it remains to show that \(\varGamma \) is classically-saturated. First of all, \(\varGamma \) is coherent since  iff there exists an index \(i\in {\mathbb {N}}\) such that
iff there exists an index \(i\in {\mathbb {N}}\) such that  , but the latter would contradict condition 1. Moreover \(\varGamma \) is deductively closed, since if
, but the latter would contradict condition 1. Moreover \(\varGamma \) is deductively closed, since if  for some \(n\in {\mathbb {N}}\), then
for some \(n\in {\mathbb {N}}\), then  and so \(B_n \in \varGamma _{n+1} \subseteq \varGamma \).
and so \(B_n \in \varGamma _{n+1} \subseteq \varGamma \).
To show the classical disjunction property, suppose that  . This implies that
. This implies that  or
or  ; without loss of generality, suppose the former is the case. Then
; without loss of generality, suppose the former is the case. Then  , and by construction \(B_{m} \in \varGamma _{m+1} \subseteq \varGamma \). Finally, to show the classical existence property suppose that
, and by construction \(B_{m} \in \varGamma _{m+1} \subseteq \varGamma \). Finally, to show the classical existence property suppose that  and let \(B_n\) be the enumeration of \(\exists x. \alpha \). Then
and let \(B_n\) be the enumeration of \(\exists x. \alpha \). Then  , and consequently
, and consequently  . By construction, there exists a term \(t\in {\mathcal {T}}_{\varSigma (A)}\) such that \(\alpha [t/x] \in \varGamma _{n+1} \subseteq \varGamma \).
. By construction, there exists a term \(t\in {\mathcal {T}}_{\varSigma (A)}\) such that \(\alpha [t/x] \in \varGamma _{n+1} \subseteq \varGamma \).
This shows that \(\varGamma \) is a classically-saturated \(\varSigma (A)\)-theory as wanted. \(\square \)
Combining the results above, we can show the connection between \(\mathsf {ClAnt}\)-saturated theories and the semantics of the logic.
Theorem 31
Given \(\varPhi \) a \(\mathsf {ClAnt}\)-saturated \(\varSigma (A)\)-theory, there exists a state \(E_{\varPhi }\) of \(\mathcal {M}^c\) such that for every \(\mathsf {ClAnt}\) formula \(\psi \) of \(\varSigma (A)\):
Proof
Define the state  and consider the theory of this state \(\varPsi \,\,{:}{=}\,\, \mathrm {Th}(\mathcal {M}^c, E_{\varPhi })\). By Lemma 29,
and consider the theory of this state \(\varPsi \,\,{:}{=}\,\, \mathrm {Th}(\mathcal {M}^c, E_{\varPhi })\). By Lemma 29,  . We want to show that also the other inclusion holds.
. We want to show that also the other inclusion holds.
Fix a classical formula \(\alpha \in \varPsi \) and suppose toward a contradiction that  . In particular, \(\alpha \) is not a consequence of
. In particular, \(\alpha \) is not a consequence of  in classical first-order logic—since
in classical first-order logic—since  is classically-saturated. By Lemma 30, then there exists a classically-saturated \(\varSigma (A)\)-theory \(\varTheta \) such that
is classically-saturated. By Lemma 30, then there exists a classically-saturated \(\varSigma (A)\)-theory \(\varTheta \) such that  and \(\alpha \notin \varTheta \). But this leads to a contradiction, since we have:
and \(\alpha \notin \varTheta \). But this leads to a contradiction, since we have:

So we established that  , and since \(\alpha \) was an arbitrary classical formula in \(\varPsi \), we also established that
, and since \(\alpha \) was an arbitrary classical formula in \(\varPsi \), we also established that  .
.
By Lemma 27, since  , we obtain that
, we obtain that  , from which the result follows. \(\square \)
, from which the result follows. \(\square \)
From the previous result, Theorem 25 follows trivially.
Proof
(Theorem 25) Consider \(\varPsi \,\,{:}{=}\,\, \mathrm {Th}(\mathcal {M}^c, E_{\varPhi })\). Since \(\mathcal {M}^c\) is \({\mathcal {T}}_{\varSigma (A)}\)-covered, \(\varPsi \) is a saturated \(\varSigma (A)\)-theory. Moreover, by Theorem 31,  , as wanted. \(\square \)
, as wanted. \(\square \)
This result, together with the saturation lemma presented in Sect. 5, leads to the completeness of the natural deduction system introduced for \(\mathsf {ClAnt}\).
5 Completeness
This section is completely devoted to the proof of completeness for the \(\mathsf {ClAnt}\) fragment. To lighten the notation in the proofs of the following lemmas, we introduce the following convention for inferences with multiple conclusions: let \(\varPhi \) and \(\varPsi \) be sets of \(\mathsf {ClAnt}\) formulas; we write  to indicate that there exists \(\psi _1,\dots ,\psi _n \in \varPsi \) such that
to indicate that there exists \(\psi _1,\dots ,\psi _n \in \varPsi \) such that  or, in case \(\varPsi \) is empty, that
or, in case \(\varPsi \) is empty, that  .
.
Lemma 32
Let \(\varPhi \cup \varPsi \cup \{\chi \}\) be a set of \(\mathsf {ClAnt}\) formulas. If  and
and  , then
, then  .
.
Proof
By hypothesis, for some \(\varphi _i,\varphi '_{i'}\in \varPhi \) and \(\psi _j,\psi '_{j'}\in \varPsi \), we haveFootnote 6

Combining the two proofs together we get

and thus  , as wanted. \(\square \)
, as wanted. \(\square \)
Lemma 33
(Saturation lemma) Consider \(\varPhi \cup \{\psi \}\) a set of \(\mathsf {ClAnt}\) \(\varSigma \)-formulas such that  . Consider the objects \({\widetilde{V}}\), \({\widetilde{\varPhi }}\) and \({\widetilde{\psi }}\) as defined in Definition 16. Then given A a countable set of parameters disjoint from \(\varSigma ({\widetilde{V}})\), there exists a \(\mathsf {ClAnt}\)-saturated \(\varSigma (A\cup {\widetilde{V}})\)-theory \(\varDelta \) such that \({\widetilde{\varPhi }} \subseteq \varDelta \) and \({\widetilde{\psi }} \notin \varDelta \).
. Consider the objects \({\widetilde{V}}\), \({\widetilde{\varPhi }}\) and \({\widetilde{\psi }}\) as defined in Definition 16. Then given A a countable set of parameters disjoint from \(\varSigma ({\widetilde{V}})\), there exists a \(\mathsf {ClAnt}\)-saturated \(\varSigma (A\cup {\widetilde{V}})\)-theory \(\varDelta \) such that \({\widetilde{\varPhi }} \subseteq \varDelta \) and \({\widetilde{\psi }} \notin \varDelta \).
Proof
This proof is an adaptation of the proof of Theorem 2 in Gabbay (1981, Sec. 3.3), developed for intuitionistic logic.
First of all, by Proposition 17 we can assume that \(\varPhi \cup \{\psi \}\) contains only sentences, and that we just need to find a \(\mathsf {ClAnt}\)-saturated \(\varSigma (A)\)-theory \(\varDelta \) such that \(\varPhi \subseteq \varDelta \) and \(\psi \notin \varDelta \). Fix an enumeration \(B_1,B_2,\dots \) of the \(\mathsf {ClAnt}\) sentences in the signature \(\varSigma (A)\).Footnote 7 We will define inductively a chain of pairs of \(\varSigma (A)\)-theories \(\left\langle \varDelta _i, \varTheta _i \right\rangle \) indexed by \(i\in {\mathbb {N}}\) such that:
-
1.
 .
. -
2.
For every index i, \(\varDelta _i \subseteq \varDelta _{i+1}\) and \(\varTheta _i \subseteq \varTheta _{i+1}\).
-
3.
\(B_n \in \varDelta _{n+1} \cup \varTheta _{n+1}\).
The plan is to take \(\varDelta \,\,{:}{=}\,\, \cup _{i\in {\mathbb {N}}} \varDelta _i\). During the construction we will impose some additional conditions to ensure \(\varDelta \) to be a \(\mathsf {ClAnt}\)-saturated \(\varSigma (A)\)-theory.
We start the construction by defining \(\left\langle \varDelta _0, \varTheta _0 \right\rangle \,\,{:}{=}\,\, \left\langle \varPhi , \{\psi \} \right\rangle \). By hypothesis condition 1 is respected; conditions 2 and 3 are trivially respected.
Suppose we already defined \(\left\langle \varDelta _n, \varTheta _n \right\rangle \) with the properties above.
By Lemma 32, we cannot have both that  and that
and that  . So we continue the proof by considering two possible (non mutually exclusive) cases: if
. So we continue the proof by considering two possible (non mutually exclusive) cases: if  and if
and if  .
.
-
1.
Case
 . We distinguish two sub-cases, depending on whether \(B_n\) is of the form \(\forall x. \varphi \) or not.
. We distinguish two sub-cases, depending on whether \(B_n\) is of the form \(\forall x. \varphi \) or not. -
(a)
Case \(B_n = \forall x. \varphi \). Consider a fresh parameter \(a\in A\) (that is, an element not appearing in \(\varDelta _n \cup \varTheta _n \cup \{B_n\}\)) and define \(\varDelta _{n+1} \,\,{:}{=}\,\, \varDelta _n\) and \(\varTheta _{n+1} \,\,{:}{=}\,\, \varDelta _n \cup \{ B_n, \varphi [a/x] \}\). Clearly conditions 2 and 3 are respected. Moreover also condition 1 holds, i.e.
 ; for otherwise, for some \(\delta _1,\dots ,\delta _h \in \varDelta _n\) and some \(\theta _1,\dots ,\theta _k \in \varTheta _n\), we would have:
; for otherwise, for some \(\delta _1,\dots ,\delta _h \in \varDelta _n\) and some \(\theta _1,\dots ,\theta _k \in \varTheta _n\), we would have:
-
(a)

So in particular  , which is a contradiction.
, which is a contradiction.
-
(b)
Case \(B_n \ne \forall x. \varphi \). In this case we simply define \(\varDelta _{n+1} \,\,{:}{=}\,\, \varDelta _n\) and \(\varTheta _{n+1} \,\,{:}{=}\,\, \varTheta _n \cup \{ B_n \}\). Conditions 1, 2 and 3 follow by construction.
-
2.
Case
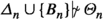 . Once again, we distinguish two sub-cases, this time depending on whether \(B_n\) is of the form
. Once again, we distinguish two sub-cases, this time depending on whether \(B_n\) is of the form  or not.
or not. -
(a)
Case
 Consider a fresh parameter \(a\in A\) and define \(\varDelta _{n+1} \,\,{:}{=}\,\, \varDelta _n \cup \{B_n, \varphi [a/x]\}\) and \(\varTheta _{n+1} \,\,{:}{=}\,\, \varTheta _n\). Clearly conditions 2 and 3 are respected. Also condition 1 holds, for otherwise:
Consider a fresh parameter \(a\in A\) and define \(\varDelta _{n+1} \,\,{:}{=}\,\, \varDelta _n \cup \{B_n, \varphi [a/x]\}\) and \(\varTheta _{n+1} \,\,{:}{=}\,\, \varTheta _n\). Clearly conditions 2 and 3 are respected. Also condition 1 holds, for otherwise:
-
(a)

and so

where T[y/a] is the proof obtained by substituting a fresh variable y for a in the proof T. Thus  , which is a contradiction.
, which is a contradiction.
-
(b)
Case
 . Define \(\varDelta _{n+1} \,\,{:}{=}\,\, \varDelta _n \cup \{B_n\}\) and \(\varTheta _{n+1} \,\,{:}{=}\,\, \varTheta _n\); clearly conditions 1, 2 and 3 are respected.
. Define \(\varDelta _{n+1} \,\,{:}{=}\,\, \varDelta _n \cup \{B_n\}\) and \(\varTheta _{n+1} \,\,{:}{=}\,\, \varTheta _n\); clearly conditions 1, 2 and 3 are respected.
Thus we built the sequence \(\left\langle \varDelta _i, \varTheta _i \right\rangle \) for \(i\in {\mathbb {N}}\), as wanted. Define \(\varDelta \,\,{:}{=}\,\, \cup _{i\in {\mathbb {N}}} \varDelta _i\) and \(\varTheta \,\,{:}{=}\,\, \cup _{i\in {\mathbb {N}}} \varTheta _i\). We want to show now that \(\varDelta \) is \(\mathsf {ClAnt}\)-saturated, that \(\varPhi \subseteq \varDelta \) and that \(\psi \notin \varDelta \).
First of all, notice that \(\varPhi \subseteq \varDelta _0 \subseteq \varDelta \). Moreover by condition 1 and 2 we have  , for otherwise there would be a finite n such that
, for otherwise there would be a finite n such that  . Consequently \(\psi \in \varTheta _0 \subseteq \varTheta \), and so \(\psi \notin \varDelta \). What is left to show is that \(\varDelta \) is \(\mathsf {ClAnt}\)-saturated.
. Consequently \(\psi \in \varTheta _0 \subseteq \varTheta \), and so \(\psi \notin \varDelta \). What is left to show is that \(\varDelta \) is \(\mathsf {ClAnt}\)-saturated.
By condition 3, we have that every sentence in \(\mathsf {ClAnt}\) is an element of \(\varDelta \cup \varTheta \). This, together with  and \(\varTheta \ne \emptyset \), ensures that \(\varDelta \) is deductively closed and \(\bot \notin \varDelta \).
and \(\varTheta \ne \emptyset \), ensures that \(\varDelta \) is deductively closed and \(\bot \notin \varDelta \).
As for the Disjunction property, suppose  . By contradiction, assume \(\varphi ,\psi \notin \varDelta \), which in turn implies \(\varphi ,\psi \in \varTheta \). In particular we would have
. By contradiction, assume \(\varphi ,\psi \notin \varDelta \), which in turn implies \(\varphi ,\psi \in \varTheta \). In particular we would have  , which is a contradiction; thus at least one among \(\varphi \) and \(\psi \) has to be in \(\varDelta \).
, which is a contradiction; thus at least one among \(\varphi \) and \(\psi \) has to be in \(\varDelta \).
For the Existence property, suppose  . Let
. Let  be the enumeration given to this sentence.
be the enumeration given to this sentence.
We have \(B_n \in \varDelta _{n+1} \cup \varTheta _{n+1}\) by condition 3. But if \(B_n \in \varTheta _{n+1}\) were the case, we would have  and consequently
and consequently  , which is a contradiction. So it follows that \(B_n \in \varDelta _{n+1}\). In particular, following the inductive construction presented above (case 2a), we have that \(\varDelta _{n+1} \,\,{:}{=}\,\, \varDelta _n \cup \{ B_n, \varphi [a/x] \}\) for some \(a\in A \subseteq {\mathcal {T}}_{\varSigma (A)}\). And so we have \(\varphi [a/x]\in \varDelta _{n+1} \subseteq \varDelta \). Since
, which is a contradiction. So it follows that \(B_n \in \varDelta _{n+1}\). In particular, following the inductive construction presented above (case 2a), we have that \(\varDelta _{n+1} \,\,{:}{=}\,\, \varDelta _n \cup \{ B_n, \varphi [a/x] \}\) for some \(a\in A \subseteq {\mathcal {T}}_{\varSigma (A)}\). And so we have \(\varphi [a/x]\in \varDelta _{n+1} \subseteq \varDelta \). Since  is an arbitrary existential sentence, it follows that \(\varDelta \) has the existence property.
is an arbitrary existential sentence, it follows that \(\varDelta \) has the existence property.
The normality condition follows from considerations completely analogous to the one in the previous paragraph. \(\square \)
Using the results we collected so far, we can completely characterize the connection between the relation  and the relations
and the relations  and \(\vDash \).
and \(\vDash \).
Theorem 34
Let \(\varPhi \cup \{\psi \}\) be \(\mathsf {ClAnt}\) formulas. Then it holds:

Proof
The left-to-right implication follows trivially, since every derivation in the deductive system for \(\mathsf {ClAnt}\) is also a derivation for the deductive system for  .
.
For the right-to-left implication, we show the contrapositive. Suppose that  . Then by Lemma 33 there exists a \(\mathsf {ClAnt}\)-saturated theory \(\varDelta \) (in an extended signature) such that \(\varPhi \subseteq \varDelta \) and \(\psi \notin \varDelta \). By Theorem 25, there exists a saturated theory \(\varPsi \) such that
. Then by Lemma 33 there exists a \(\mathsf {ClAnt}\)-saturated theory \(\varDelta \) (in an extended signature) such that \(\varPhi \subseteq \varDelta \) and \(\psi \notin \varDelta \). By Theorem 25, there exists a saturated theory \(\varPsi \) such that  , and so in particular \(\varPhi \subseteq \varPsi \) and \(\psi \notin \varPsi \). Since \(\varPsi \) is deductively closed with respect to
, and so in particular \(\varPhi \subseteq \varPsi \) and \(\psi \notin \varPsi \). Since \(\varPsi \) is deductively closed with respect to  , it follows that
, it follows that  . \(\square \)
. \(\square \)
Theorem 35
(Completeness) Let \(\varPhi \cup \{\psi \}\) be \(\mathsf {ClAnt}\) formulas. Then it holds:

Proof
We prove the result by contraposition: suppose that  . By Lemma 33, given A a countable set of fresh parameters there exists a \(\mathsf {ClAnt}\)-saturated \(\varSigma ({\widetilde{V}}\cup A)\)-theory \(\varDelta \) such that \({\widetilde{\varPhi }} \subseteq \varDelta \) and \({\widetilde{\psi }} \notin \varDelta \). By Theorem 31, given \(\mathcal {M}^c\) the canonical model for the signature \(\varSigma ({\widetilde{V}}\cup A)\), we have
. By Lemma 33, given A a countable set of fresh parameters there exists a \(\mathsf {ClAnt}\)-saturated \(\varSigma ({\widetilde{V}}\cup A)\)-theory \(\varDelta \) such that \({\widetilde{\varPhi }} \subseteq \varDelta \) and \({\widetilde{\psi }} \notin \varDelta \). By Theorem 31, given \(\mathcal {M}^c\) the canonical model for the signature \(\varSigma ({\widetilde{V}}\cup A)\), we have  . Thus in particular \(\mathcal {M}^c, E_\varDelta \vDash {\widetilde{\varPhi }}\) and \(\mathcal {M}^c, E_\varDelta \not \vDash {\widetilde{\psi }}\).
. Thus in particular \(\mathcal {M}^c, E_\varDelta \vDash {\widetilde{\varPhi }}\) and \(\mathcal {M}^c, E_\varDelta \not \vDash {\widetilde{\psi }}\).
Define the assignment \(g: V \rightarrow D\) such that \(g(x) = ({\widetilde{x}})^{\mathcal {M}}\). An easy induction shows that, for every formula \(\chi \) in the signature \(\varSigma \) with free variables in V we have
\(\mathcal {M}^c, E_{\varDelta } \vDash _g \chi \) iff \(\mathcal {M}^c, E_{\varDelta } \vDash {\widetilde{\chi }}\). In particular, it follows that \(\mathcal {M}^c, E_{\varDelta } \vDash _g \varPhi \) and \(\mathcal {M}^c, E_{\varDelta } \nvDash _g \psi \). Thus \(\varPhi \not \vDash \psi \), as wanted. \(\square \)
6 Language with Equality
Notice that in defining the syntax of  (Definition 1) we did not consider the equality symbol. There are at least two ways to enhance the semantics of
(Definition 1) we did not consider the equality symbol. There are at least two ways to enhance the semantics of  with an equality symbol: we can consider a rigid or a non-rigid interpretation. Both are described in detail in Ciardelli (2016, Ch. 4).Footnote 8
with an equality symbol: we can consider a rigid or a non-rigid interpretation. Both are described in detail in Ciardelli (2016, Ch. 4).Footnote 8
In the rigid interpretation, the semantic clause for equality is
That is, \(t_1 = t_2\) holds if and only if the two elements are interpreted as the same element of \(D^\mathcal {M}\).
In the second case, we want the interpretation of equality to be world-dependent, like the interpretation of other relation symbols. To achieve this, we need a small generalization of the notion of first-order model described in Footnote 3: additionally, we require a first-order model to specify an equivalence relation \(\sim \) (the interpretation of the equality symbol) that is required to be a congruence with respect to the interpretation of the function and relation symbols. In this case, the corresponding semantical clause for equality is
That is, \(t_1\) and \(t_2\) are interpreted as elements of \(D^{\mathcal {M}}\) which every world in s consider to be identical.
Let us refer to \(\vDash ^=\) and \(\vDash ^\sim \) as the semantical relations corresponding to Clauses 1 and 2 respectively. To account for these two extensions of the language, we can modify the deductive system in Definition 9 by adding rules 1-3 for the rigid equality; and rules 1–2 for the non-rigid equality.Footnote 9

As for the case without equality, it is still an open question whether these deductive systems are complete. However, we can show that the corresponding restricted systems for \(\mathsf {ClAnt}\) are complete.
Theorem 36
(Completeness for the language with equality) Consider the natural deduction systems  and
and  obtained by adding to the system in Definition 14 Rules 1–3 and Rules 1–2 respectively. Then, given \(\varPhi \cup \{\psi \}\) a set of \(\mathsf {ClAnt}\) formulas (possibly containing \(=\)), we have:
obtained by adding to the system in Definition 14 Rules 1–3 and Rules 1–2 respectively. Then, given \(\varPhi \cup \{\psi \}\) a set of \(\mathsf {ClAnt}\) formulas (possibly containing \(=\)), we have:

Proof
(Sketch) We want to prove analogues of Theorem 35 for the new relations introduced. To achieve this, we need analogues of Definition 20 and Lemma 21 for the case with rigid and non-rigid equality, which follow again by adapting the proof of Theorem 2.3.3 in Hodges (1993). All the other proofs in this paper are independent from the equality symbols being in the language, including the proof of Theorem 35. \(\square \)
7 Conclusions
In this paper we introduced the \(\mathsf {ClAnt}\) fragment of  , extending the mention-some and mention-all fragments. We presented a natural deduction system for \(\mathsf {ClAnt}\), specializing the one proposed in Ciardelli (2016, Ch. 4) for
, extending the mention-some and mention-all fragments. We presented a natural deduction system for \(\mathsf {ClAnt}\), specializing the one proposed in Ciardelli (2016, Ch. 4) for  . We introduced \(\mathsf {ClAnt}\)-saturated theories, which stem from the deduction system presented, and showed (1) these theories are characterized by their classical fragment and (2) they are exactly the restrictions to the \(\mathsf {ClAnt}\) fragment of saturated theories for the whole language. This allowed us to prove the main result of the paper, that is, the completeness of the natural deduction system through a canonical model construction.
. We introduced \(\mathsf {ClAnt}\)-saturated theories, which stem from the deduction system presented, and showed (1) these theories are characterized by their classical fragment and (2) they are exactly the restrictions to the \(\mathsf {ClAnt}\) fragment of saturated theories for the whole language. This allowed us to prove the main result of the paper, that is, the completeness of the natural deduction system through a canonical model construction.
The protagonists in the proof abovementioned are the \(\mathsf {ClAnt}\)-saturated theories: by studying their properties, we were able to adapt the canonical model technique to (a fragment of)  . The same approach can be applied to fragments of the logic satisfying properties (1) and (2) above, obtaining analogous completeness results; as of now it is not known if a proper extension of \(\mathsf {ClAnt}\) with said properties exists. Potentially, a variation of the approach could be applied to the logic
. The same approach can be applied to fragments of the logic satisfying properties (1) and (2) above, obtaining analogous completeness results; as of now it is not known if a proper extension of \(\mathsf {ClAnt}\) with said properties exists. Potentially, a variation of the approach could be applied to the logic  , although it is not known whether property (1) holds for the whole language. Further investigations in this direction are left for future work.
, although it is not known whether property (1) holds for the whole language. Further investigations in this direction are left for future work.
Change history
15 February 2022
Open access funding note is included
Notes
The reader might wonder why we do not introduce a symbol \({\overline{\forall }}\) dual to the quantifier
 , that is, defined by the shorthand
, that is, defined by the shorthand
 . There are two main reasons. Firstly, the formulas
\(\forall x. \lnot \lnot \varphi \) and
. There are two main reasons. Firstly, the formulas
\(\forall x. \lnot \lnot \varphi \) and
 are provably equivalent in
are provably equivalent in
 , thus making the addition of
\({\overline{\forall }}\) to the system redundant. Secondly, the formula
\({\overline{\forall }} x. \varphi \) so defined is always equivalent to a classical formula (Definition 2), and thus
\({\overline{\forall }}\) would not play the role of a question-forming operator as the notation would suggest.
, thus making the addition of
\({\overline{\forall }}\) to the system redundant. Secondly, the formula
\({\overline{\forall }} x. \varphi \) so defined is always equivalent to a classical formula (Definition 2), and thus
\({\overline{\forall }}\) would not play the role of a question-forming operator as the notation would suggest.In this context, a first-order model consists of a domain D and an interpretation of each relation (resp. function) symbol of \(\varSigma \) as a relation (resp. function) symbol of \(\varSigma \) of the corresponding arity over D.
If the set \(\varPhi \) and \(\psi \) have a common free variable, let us say x, \({\widetilde{\varPhi }}\) and \({\widetilde{\psi }}\) are obtained by substituting the free occurrences of x with the same formal parameter \({\widetilde{x}}\).
Recall that, by Lemma 10,
 amounts to classical entailment when restricted to classical formulas.
amounts to classical entailment when restricted to classical formulas.In the natural deduction proofs that follow we will use a single line for the application of an instance of a rule; while we will use a double line for a subproof. On the right of a single line we will write the name of the rule applied; on the right of a double line we will write a label naming the subproof.
Notice that this can be done without the use of the axiom of choice since we are considering a countable signature \(\varSigma \) and a countable set A.
Rules 1–2 are the standard rules for equality found in natural deduction systems for intuitionistic logic, while Rule 3 is thoroughly discussed in Ciardelli (2016, Sec. 4.5).
References
Ciardelli, I. (2009). Inquisitive semantics and intermediate logics. M.Sc. thesis, University of Amsterdam.
Ciardelli, I. (2014). Modalities in the realm of questions: Axiomatizing inquisitive epistemic logic. In R. Goré, B. Kooi, & A. Kurucz (Eds.), Advances in Modal Logic (AiML) (pp. 94–113). College Publications.
Ciardelli, I. (2016). Questions in logic. Institute for logic, language and computation. Ph.D. thesis, University of Amsterdam.
Ciardelli, I., & Roelofsen, F. (2011). Inquisitive logic. Journal of Philosophical Logic, 40(1), 55–94.
Ciardelli, I., Groenendijk, J., & Roelofsen, F. (2018). Inquisitive semantics. Oxford University Press.
Ciardelli, I., Iemhoff, R., & Yang, F. (2020). Questions and dependency in intuitionistic logic. Notre Dame Journal of Formal Logic, 61(1), 75–115, 1.
Gabbay, D. (1981). Semantical investigations in Heyting’s intuitionistic logic (Vol. 148). Springer.
Gianluca, G., & Ivano, C. (2019). An Ehrenfeucht-Fraïssé game for inquisitive first-order logic. In A. Silva, S. Staton, P. Sutton, & C. Umbach (Eds.), Language, logic, and computation (pp. 166–186). Springer.
Grilletti, G. (2019). Disjunction and existence properties in inquisitive first-order logic. Studia Logica, 107(6), 1199–1234.
Groenendijk, J. (1999). The logic of interrogation. In T. Matthews & D. Strolovitch (Eds.), Semantics and linguistic theory (pp. 109–126). Cornell University Press.
Hodges, W. (1993). Model theory. Encyclopedia of mathematics and its applications: Cambridge University Press.
Katsuhiko, S. (2011). First-order inquisitive pair logic. In M. Banerjee & A. Seth (Eds.), Logic and its applications (pp. 147–161). Springer.
Punčochář, V. (2015). Weak negation in inquisitive semantics. Journal of Logic, Language, and Information, 24(3), 323–355.
Punčochář, V. (2019). Substructural inquisitive logics. The Review of Symbolic Logic, 12(2), 296–330.
Roelofsen, F. (2013). Algebraic foundations for the semantic treatment of inquisitive content. Synthese, 190(1), 79–102.
ten Cate, B., & Shan, C.-C. (2007). Axiomatizing Groenendijks logic of interrogation. In M. Aloni, A. Butler, & P. Dekker (Eds.), Questions in dynamic semantics (pp. 63–82). Elsevier.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author gratefully acknowledges funding from the European Research Council (ERC, grant agreement number 680220). The author would also like to thank Ivano Ciardelli, Thom van Gessel and Floris Roelofsen for useful discussion on the manuscript and the anonymous reviewers for their comments and suggestions.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grilletti, G. Completeness for the Classical Antecedent Fragment of Inquisitive First-Order Logic. J of Log Lang and Inf 30, 725–751 (2021). https://doi.org/10.1007/s10849-021-09341-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-021-09341-y




 , then
, then  , then
, then 
 formulas in the signature
formulas in the signature  sentences in the signature
sentences in the signature  is a classically-saturated
is a classically-saturated  .
. , then
, then  .
. , then
, then 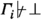 .
. and
and  ; condition 2 is trivially satisfied; condition 3 follows from the
; condition 2 is trivially satisfied; condition 3 follows from the  and
and  . So by condition 3 and the
. So by condition 3 and the  . Define
. Define  and
and  ; Condition 2 trivially holds; Condition 3 follows from the
; Condition 2 trivially holds; Condition 3 follows from the  . Define
. Define  .
. . We distinguish two sub-cases, depending on whether
. We distinguish two sub-cases, depending on whether  ; for otherwise, for some
; for otherwise, for some 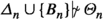 . Once again, we distinguish two sub-cases, this time depending on whether
. Once again, we distinguish two sub-cases, this time depending on whether  or not.
or not.  Consider a fresh parameter
Consider a fresh parameter  . Define
. Define  , that is, defined by the shorthand
, that is, defined by the shorthand
 . There are two main reasons. Firstly, the formulas
. There are two main reasons. Firstly, the formulas
 are provably equivalent in
are provably equivalent in
 , thus making the addition of
, thus making the addition of
 amounts to classical entailment when restricted to classical formulas.
amounts to classical entailment when restricted to classical formulas.