Abstract
Euclidean diagrammatic reasoning refers to the diagrammatic inferential practice that originated in the geometrical proofs of Euclid’s Elements. A seminal philosophical analysis of this practice by Manders (‘The Euclidean diagram’, 2008) has revealed that a systematic method of reasoning underlies the use of diagrams in Euclid’s proofs, leading in turn to a logical analysis aiming to capture this method formally via proof systems. The central premise of this paper is that our understanding of Euclidean diagrammatic reasoning can be fruitfully advanced by confronting these logical and philosophical analyses with the field of cognitive science. Surprisingly, central aspects of the philosophical and logical analyses resonate in very natural ways with research topics in mathematical cognition, spatial cognition and the psychology of reasoning. The paper develops these connections, concentrating on four issues: (1) the cognitive origins of Euclidean diagrammatic reasoning, (2) the cognitive representations of spatial relations in Euclidean diagrams, (3) the nature of the cognitive processes and cognitive representations involved in Euclidean diagrammatic reasoning seen as a form of visuospatial relational reasoning and (4) the complexity of Euclidean diagrammatic reasoning for the human cognitive system. For each of these issues, our analysis generates concrete experiment proposals, opening thereby the way for further empirical investigations. The paper is thus a prolegomenon to a research program on Euclidean diagrammatic reasoning at the crossroads of logic, philosophy and cognitive science.














Similar content being viewed by others
Notes
Throughout the paper we use the term ‘elementary Euclidean geometry’ to refer to what Tarski calls ‘elementary geometry’ in the opening sentence of (Tarski 1959), namely: “the body of notions and theorems which, following the tradition of Euclid’s Elements, form the subject matter of geometry courses in secondary schools” (Tarski 1959, p. 16).
Giaquinto (2007) is a typical example of work in the philosophy of mathematics directly informed by cognitive science.
The paper restricts its focus on these three subfields. This is by no mean an exhaustive list of subfields of cognitive science relevant to a cognitive investigation of Euclidean diagrammatic reasoning. In the conclusion of this paper, we will indicate other important connections to be explored, extending to other subfields than the ones mentioned here.
On this see section 4.2.2 of Manders (2008).
What this restricted conception removes from consideration most conspicuously are the properties of objects within diagrams—the exact straightness of a line, for instance. Moreover, it also removes from consideration exact relations which are not relations between the magnitudes of objects in diagrams. An example is the relation of the tangency of a line to a circle.
An anonymous referee has brought to our attention that between the verbal presentations of
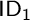 and
and 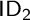 and the visual presentations given by Fig. 2 sits an important cognitive question: how are verbal formulations of the premises and conclusion of a Euclidean diagrammatic inference interpreted visually? Such an interpretation appears to be central to the realization of concrete diagrams like those of Fig. 2, as different interpretations can lead to different co-exact features being realized concretely. The cognitive basis of the interpretative process is thus a central issue in understanding the interaction with concrete diagrams in the mathematical practice of Euclid’s Elements. It is however beyond the scope of this paper. A full study of it is a task for future research.
and the visual presentations given by Fig. 2 sits an important cognitive question: how are verbal formulations of the premises and conclusion of a Euclidean diagrammatic inference interpreted visually? Such an interpretation appears to be central to the realization of concrete diagrams like those of Fig. 2, as different interpretations can lead to different co-exact features being realized concretely. The cognitive basis of the interpretative process is thus a central issue in understanding the interaction with concrete diagrams in the mathematical practice of Euclid’s Elements. It is however beyond the scope of this paper. A full study of it is a task for future research.A highly critical analysis of the \(\mathbf{Eu}\) approach here described has recently appeared (Miller 2012). Miller identifies some serious formal deficiencies with the proof system as developed in Mumma (2006), and claims that these deficiencies result from those features of \(\mathbf{Eu}\) that distinguish it from the system he developed in Miller (2007). Miller’s diagnosis is however mistaken. The features underlying the problems he identifies are not systemic but rather local and isolated. Rectifying the problems is simply a matter of removing the bugs in the presentation of \(\mathbf{Eu}\) in Mumma (2006). A response paper demonstrating this has been submitted (Mumma 2013). As all the resulting modifications to \(\mathbf{Eu}\) are at the local level, they have no bearing on the general framework of \(\mathbf{Eu}\) as a formal system, and so have no bearing on our general proposals for utilizing the system for empirical research in Euclidean diagrammatic reasoning.
In Izard et al. (2011a, p. 330), an intuition is defined as “a form of knowledge that is accessible to explicit report, although its justification is not”. An intuition is then said to be universal when it is “present in all normally developing human beings, irrespective of their environment, level of education etc.”.
This study investigates also the capacity of participants to use geometrical clues to locate objects in the world based on information from maps. This part of the study is not directly relevant for Euclidean diagrammatic reasoning and will not be discussed here.
The terminology used here for the classification of concepts and for concept names is that of Dehaene et al. (2006).
In the terminology of Sect. 2, we would reformulate the principle as ‘given a line and a point off this line, one can always place a unique line such that this point is on it, and it would never intersect the first line’.
In the terminology of the test, the authors use the phrase “lines crossing” to refer to the intersection relation, and the phrase “line going through points” to refer to the on relation.
In Izard et al. (2011b), accompanying illustrations are provided in the task in order to help visualization and to support the narration. In line with the experimental methodology of Izard et al. (2011b), the sketches we are providing in Fig. 9 aim to fulfill the same role. An anonymous referee has pointed out to us that one may wonder whether such illustrations can influence performances in the task, and if so how they are used by participants. These issues are not directly addressed in Izard et al. (2011b), and we suspect that substantial theoretical and experimental work is required to answer them.
For another discussion of the relation between cognitive intuitions of space and the emergence of geometry as a mathematical theory, see De Cruz (2009).
Kosslyn et al. (1989) explained this hemispheric specialization by arguing that the left hemisphere is involved in category formation in several aspects of language, while the right hemisphere plays an important role in navigation for which coordinate and metric information is central.
New aspects of the coordinate/categorical distinction have been investigated recently by van der Ham (2010), in particular concerning its temporal aspects in working memory and its role in perception and memory in real life situations.
Notice that the idea of representing a co-exact relation as an equivalence class of specific instantiations satisfying the relation is central to the logical system \(\mathbf{Eu}\): a co-exact spatial relation is captured through an equivalence class of \(\mathbf{Eu}\) diagrams instantiating the spatial configuration of geometric objects described by the relation, while a given \(\mathbf{Eu}\) diagram can be seen as conveying specific information relative to the spatial locations of the geometric objects within an \(n \times n\) array.
It is important to emphasize here that our claim holds for our restrictive use of the exact/co-exact distinction, in particular where exact relations only concern equality or inequality relations between length, angle or area magnitudes. In the more general account of the distinction provided by Manders, one has to be very careful in classifying exact relations as coordinate ones. In particular, examples such as the relation of tangency between a line and a circle—an exact relation according to Manders—are not directly classified as coordinate in the sense of Kosslyn’s distinction, and might even be classified as categorical. It is likely that the full account provided by Manders of the exact/co-exact distinction requires additional categories than the coordinate and categorical ones.
A large part of the psychological literature on relational reasoning has focused on transitive inferences, i.e., inferences whose validity comes from the transitive property of the relation involved. Inference \({\mathsf {IR}}\) is an example of transitive inference. The mental rule and mental model theories, however, have the capacity to deal with other forms of relational reasoning than transitive inferences. We shall mention that transitive inferences play a very small role in Euclidean diagrammatic reasoning.
Notice that the VIA view is precisely what Knauff opposes with his three-stage theory.
Knauff (2009) emphasizes that the first stage elicits activity mainly in the visual areas (OCT). However, this might be a consequence of the study (Fangmeier et al. 2006) motivating the theory. In this study, premises and conclusion are provided visually: for instance, the premise ‘\(V\) is to the left of \(X\)’ is presented via a picture in which only \(V\) and \(X\) are represented, and where \(V\) is to the left of \(X\). In the context of Euclidean diagrammatic reasoning, there does not seem to be any possibility of presenting premises and conclusion visually: one would need instead to specify explicitly the spatial relations between the objects, eventually in the form of construction steps. Indeed, (Knauff 2009, p. 119) recognizes that visual images in the first stage can be generated top–down from memory. In this case, semantic knowledge about spatial relations would have to be solicited. Thus, our adaptation of the three-stage theory does not depart from Knauff (2009), but emphasizes modifications necessary for the situation in which premises are not presented visually.
Notice that modifications of the three-stage theory at the level of spatial representations might have a direct impact on predictions of the theory concerning neural activity. Notice also that if one wishes to develop an account of spatial representations as grounded in the visual system, this would lead to a role for visual representations completely different from the one postulated by the VIA view.
An interesting line of research to explore further here concerns the role of these mechanisms in the context of problem solving tasks such as the ones investigated in Koedinger and Anderson (1990).
The nature of our approach can perhaps be clarified by situating it with respect to David Marr’s three levels of cognitive analysis (Marr 1982). Accordingly, a cognitive analysis can be carried out at the computational (or functional) level, algorithmic level or implementational level. Clearly, the philosophical and logical analyses of Euclidean diagrammatic reasoning given in Sect. 2 sit on the functional level as they describe Euclidean diagrammatic reasoning in terms of the types of information and inferences it consists in. Most of the paper can then be seen as the development of a cognitive perspective on Euclidean diagrammatic reasoning situated at the algorithmic level as our efforts have been devoted to identifying what could be the cognitive representations and processes used by the cognitive system to carry out Euclidean diagrammatic reasoning. We have not addressed the implementational level in this paper. Since the \(E\) and \(\mathbf{Eu}\) systems can be seen as formal models at the functional level, an anonymous referee has suggested to us that further progress can be made on the formal front by trying to develop formal models at the algorithmic level. To this end, one might then take inspiration from the field of spatial qualitative reasoning (Renz and Nebel 2007), and in particular from formal models for representing and reasoning with topological information (Randell et al. 1992).
It would be interesting also to explore potential connections with theoretical and computational models of visual imagery, such as for instance the computational imagery theory of Glasgow and Papadias (1992). However, even though such frameworks often deal with visual and spatial representations, they take visual representations to be primary while we adopt the opposite perspective whereby spatial representations are primary. Further research is required to understand how the two perspectives can interact with one another.
References
Avigad, J., Dean, E., & Mumma, J. (2009). A formal system for Euclid’s Elements. Review of Symbolic Logic, 2(4), 700–768.
Baciu, M., Koenig, O., Vernier, M., Bedoin, N., Rubin, C., & Segebarth, C. (1999). Categorical and coordinate spatial relations: fMRI evidence for hemispheric specialization. NeuroReport, 10(6), 1373–1378.
Barsalou, L. (1999). Perceptual symbol systems. Behavioral and Brain Sciences, 22(04), 577–660.
Barsalou, L. (2008). Grounded cognition. Annual Review of Psychology, 59, 617–645.
Christoff, K., Prabhakaran, V., Dorfman, J., Zhao, Z., Kroger, J., Holyoak, K., et al. (2001). Rostrolateral prefrontal cortex involvement in relational integration during reasoning. NeuroImage, 14(5), 1136–1149.
Clark, A., & Chalmers, D. (1998). The extended mind. Analysis, 58, 7–19.
De Cruz, H. (2009). An enhanced argument for innate elementary geometric knowledge and its philosophical implications. In B. van Kerkhove (Ed.), New perspectives on mathematical practices, essays in philosophy and history of mathematics (pp. 185–206). New Jersey: World Scientific.
Dehaene, S., Izard, V., Pica, P., & Spelke, E. (2006). Core knowledge of geometry in an Amazonian indigene group. Science, 311(5759), 381–384.
Euclid (anc.) The thirteen books of Euclid’s elements.
Fangmeier, T., Knauff, M., Ruff, C., & Sloutsky, V. (2006). fMRI evidence for a three-stage model of deductive reasoning. Journal of Cognitive Neuroscience, 18(3), 320–334.
Giaquinto, M. (2007). Visual thinking in mathematics: An epistemological study. Oxford: Oxford University Press.
Glasgow, J., & Papadias, D. (1992). Computational imagery. Cognitive Science, 16(3), 355–394.
Goel, V., Gold, B., Kapur, S., & Houle, S. (1998). Neuroanatomical correlates of human reasoning. Journal of Cognitive Neuroscience, 10(3), 293–302.
Goodwin, G., & Johnson-Laird, P. (2005). Reasoning about relations. Psychological Review, 112(2), 468–493.
Halford, G., Wilson, W., & Phillips, S. (1998). Processing capacity defined by relational complexity: Implications for comparative, developmental, and cognitive psychology. Behavioral and Brain Sciences, 21(06), 803–831.
Halford, G., Baker, R., McCredden, J., & Bain, J. (2005). How many variables can humans process? Psychological Science, 16(1), 70–76.
Halford, G., Wilson, W., & Phillips, S. (2010). Relational knowledge: The foundation of higher cognition. Trends in Cognitive Sciences, 14(11), 497–505.
Hegarty, M., & Stull, A. (2012). Visuospatial thinking. In K. Holyoak & R. Morrison (Eds.), The Oxford handbook of thinking and reasoning (pp. 606–630). Oxford: Oxford University Press.
Hutchins, E. (1999). Cognitive artifacts. In R. Wilson & F. Keil (Eds.), The MIT encyclopedia of the cognitive sciences (pp. 126–128). Cambridge, MA: MIT Press.
Izard, V., Pica, P., Dehaene, S., Hinchey, D., & Spelke, E. (2011a). Geometry as a universal mental construction. In E. Brannon & S. Dehaene (Eds.), Space, time and number in the brain: Searching for the foundations of mathematical thought, no. XXIV in attention and performance (pp. 319–332). Oxford: Oxford University Press.
Izard, V., Pica, P., Spelke, E., & Dehaene, S. (2011b). Flexible intuitions of Euclidean geometry in an Amazonian indigene group. Proceedings of the National Academy of Sciences, 108(24), 9782–9787.
Jager, G., Postma, A., et al. (2003). On the hemispheric specialization for categorical and coordinate spatial relations: A review of the current evidence. Neuropsychologia, 41(4), 504–515.
Johnson-Laird, P., Byrne, R., & Tabossi, P. (1989). Reasoning by model: The case of multiple quantification. Psychological Review, 96(4), 658–673.
Knauff, M. (2009). A neuro-cognitive theory of deductive relational reasoning with mental models and visual images. Spatial Cognition & Computation, 9(2), 109–137.
Knauff, M. (2013). Space to reason: A spatial theory of human thought. Cambridge, MA: MIT Press.
Koedinger, K., & Anderson, J. (1990). Abstract planning and perceptual chunks: Elements of expertise in geometry. Cognitive Science, 14(4), 511–550.
Kosslyn, S. (1987). Seeing and imagining in the cerebral hemispheres: A computational approach. Psychological Review, 94(2), 148–175.
Kosslyn, S. (1994). Image and brain: The resolution of the imagery debate. Cambridge, MA: MIT press.
Kosslyn, S., Koenig, O., Barrett, A., Cave, C., Tang, J., & Gabrieli, J. (1989). Evidence for two types of spatial representations: Hemispheric specialization for categorical and coordinate relations. Journal of Experimental Psychology: Human Perception and Performance, 15(4), 723–735.
Kosslyn, S., Chabris, C., Marsolek, C., & Koenig, O. (1992). Categorical versus coordinate spatial relations: Computational analyses and computer simulations. Journal of Experimental Psychology: Human Perception and Performance, 18(2), 562–577.
Kosslyn, S., Thompson, W., Gitelman, D., & Alpert, N. (1998). Neural systems that encode categorical versus coordinate spatial relations: PET investigations. Psychobiology, 26(4), 333–347.
Laeng, B. (1994). Lateralization of categorical and coordinate spatial functions: A study of unilateral stroke patients. Journal of Cognitive Neuroscience, 6(3), 189–203.
Manders, K. (2008). The Euclidean diagram. In P. Mancosu (Ed.), Philosophy of mathematical practice. Oxford: Oxford University Press.
Margolis, E., & Laurence, S. (2007). Creations of the mind: Theories of artifacts and their representation. Oxford: Oxford University Press.
Marr, D. (1982). Vision: A computational investigation into the human representation and processing of visual information. San Francisco, CA: Freeman.
Miller, N. (2007). Euclid and his twentieth century rivals: Diagrams in the logic of Euclidean geometry. Stanford: CSLI Publications.
Miller, N. (2012). On the inconsistency of Mumma’s Eu. Notre Dame Journal of Formal Logic, 53(1), 27–52.
Mumma, J. (2006). Intuition formalized: ancient and modern methods of proof in elementary geometry. Ph.D. Thesis, Carnegie Mellon University.
Mumma, J. (2010). Proofs, pictures, and Euclid. Synthese, 175(2), 255–287.
Mumma, J. (2013). Refining and elaborating Eu: a response to Miller’s ‘on the inconsistency of Eu’, (submitted).
Norman, D. (1991). Cognitive artifacts. In J. Carroll (Ed.), Designing interaction: Psychology at the human–computer interface (pp. 17–38). Cambridge: Cambridge University Press.
Palermo, L., Bureca, I., Matano, A., & Guariglia, C. (2008). Hemispheric contribution to categorical and coordinate representational processes: A study on brain-damaged patients. Neuropsychologia, 46(11), 2802–2807.
Randell, D., Cohn, A. & Cui, Z. (1992). A spatial logic based on regions and connection. In Nebel, B., Swartout, W., & Rich, C. (eds) Proceedings of the 3rd conference on principles of knowledge representation and reasoning, vol. 92, (pp 165–176). Cambridge, MA: Morgan Kaufmann.
Renz, J., & Nebel, B. (2007). Qualitative spatial reasoning using constraint calculi. In M. Aiello, I. Pratt-Hartmann, & J. van Benthem (Eds.), Handbook of spatial logics (pp. 161–215). Berlin: Springer.
Rips, L. (1994). The psychology of proof: Deductive reasoning in human thinking. Cambridge, MA: The MIT Press.
Spelke, E. (2011). Natural number and natural geometry. In E. Brannon & S. Dehaene (Eds.), Space, time and number in the brain: Searching for the foundations of mathematical thought, no XXIV in attention and performance (pp. 287–317). Oxford: Oxford University Press.
Spelke, E., & Kinzler, K. (2007). Core knowledge. Developmental Science, 10(1), 89–96.
Stenning, K. (2002). Seeing reason: Image and language in learning to think. Oxford: Oxford University Press.
Tarski, A. (1959). What is elementary geometry? In P. Suppes, A. Tarski, & L. Henkin (Eds.), The axiomatic method: With special reference to geometry and physics (1st ed., pp. 16–29). Amsterdam: North-Holland.
Trojano, L., Conson, M., Maffei, R., & Grossi, D. (2006). Categorical and coordinate spatial processing in the imagery domain investigated by rTMS. Neuropsychologia, 44(9), 1569–1574.
Tversky, B. (2005). Visuospatial reasoning. In K. Holyoak & R. Morrison (Eds.), The Cambridge handbook of thinking and reasoning (pp. 209–240). Cambridge: Cambridge University Press.
van der Ham, C. (2010). Thinking left and right: Neurocognitive studies on spatial relation processing. Ph.D. Thesis, Utrecht University.
Waltz, J., Knowlton, B., Holyoak, K., Boone, K., Mishkin, F., de Menezes, Santos M., et al. (1999). A system for relational reasoning in human prefrontal cortex. Psychological Science, 10(2), 119–125.
Acknowledgments
Parts of this paper have been presented at the Logic and Cognition 2012 Conference in Poznań (Poland, May 2012), the International Conference on Thinking in London (UK, July 2012) and the Logic and Cognition Workshop at ESSLLI in Opole (Poland, August 2012). We would like to thank the audiences of these events for helpful feedback and comments, in particular Markus Knauff and Michiel van Lambalgen for stimulating discussions. We are thankful to Jean Paul van Bendegem for providing comments on the whole manuscript. Finally, we are very grateful to Jakub Szymanik, Rineke Verbrugge and three anonymous referees for providing extensive comments that led to substantial improvements of the paper. Yacin Hamami acknowledges support from a doctoral fellowship of the Research Foundation Flanders (FWO).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hamami, Y., Mumma, J. Prolegomena to a Cognitive Investigation of Euclidean Diagrammatic Reasoning. J of Log Lang and Inf 22, 421–448 (2013). https://doi.org/10.1007/s10849-013-9182-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-013-9182-8





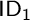 and
and 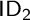 and the visual presentations given by Fig.
and the visual presentations given by Fig.