Abstract
The maturation of the physical image has made apparent the limits of our scientific understanding of fundamental reality. These limitations serve as motivation for a new form of metaphysical inquiry that restricts itself to broadly scientific methods. Contributing towards this goal we combine the mathematical universe hypothesis as developed by Max Tegmark with the axioms of Stewart Shapiro’s structure theory. The result is a theory we call the Theory of the Structural Multiverse (TSM). The focus is on informal theory development and constraint satisfaction. Some empirical consequences of the theory are worked out, in particular the feasibility of a predictive observer selection effect. The explanatory, unifying, and generative powers of the theory are found to substantially support the theory. The TSM is demonstrated to be an empirically significant scientific theory that is foundational to and continuous with the rest of the scientific image.
Similar content being viewed by others
Notes
Arithmetic was formalized in this way by Peano and later geometry and analysis were formalized by Hilbert and his colleagues.
Tegmark (1998) assembles an illustrative diagram to visualize the connections between the formal theories corresponding to the various branches of natural mathematics.
This is true for non-algebraic second-order theories like arithmetic. First-order theories of infinite structures are non-categorical in that they suffer from the Löwenheim–Skolem theorems that produce unintended non-isomorphic models even for non-algebraic theories. There are also categorical and algebraic branches of mathematics that intend to describe not a single structure but a class of them, such as group theory. There are the regular exceptions to the rule, such as when we try to model set theory in the cumulative hierarchy itself. For a detailed review of second-order model theory as a foundation for mathematics see Shapiro (1994).
Shapiro and Resnik call such structures abstract though they do not offer solutions as to how abstract reality relates to physical reality. Shapiro considered the possibility that physical reality was no different than mathematical reality but did not fully elaborate on the consequences of such a conception. We are left with separate physical and mathematical realms and as such the global ontology increases and is more complex.
The concept of a universe is typically applied with little theoretical rigor to what are elsewhere referred to O-regions, parallel realities, inflationary pockets, and parallel universes. Tegmark’s multiverse hierarchy helps sort out the mess but we would go further and limit the application of the concept of a universe to his level 4 multiverse composed of mathematical structures alone.
This is the main deviation from structure theory and the main difference between structural universes and mathematical structures. All structural universes are mathematical structures, but only continuous mathematical structures are structural universes. Mathematical structures can include collections of disconnected universes, but universes must be unified wholes. Just because the cumulative hierarchy is big enough to model two disconnected structural universes simultaneously does not mean that any new universe has been described as a result. A single mathematical structure can actually describe several structural universes.
This axiom is needed to secure the existence of the natural number structure and all larger infinite structures that are based on it.
The addition of certain relations may result in inconsistency. The structure resulting from an addition must also satisfy the rest of the axioms, in particular the existence axiom.
This definition of equivalence is preferable to a simple isomorphic requirement because isomorphism is too strict for recognizing sameness of structure. If two structures have different relations but the relations of one can be defined in terms of the relations the other they should be considered equivalent. There still remain several issues that limit our ability to propose valid equivalence criteria, but it seems that at this point there will be no detectable empirical consequences. See Resnik (1997).
The present axiom gives the criteria for recognizing structural existence. In Sect. 3.2 on explanations we discuss further the general problem of existence and offer a definition in structuralist terms. Shaprio points out that we have reason to believe in mathematical structures that can be described by coherent theories, but there may also exist structures that cannot be described by such theories.
Scientific theories are distinguished from philosophical or metaphysical theories of reality in that they rigorously specify a set of models and they link those models to observational procedures.
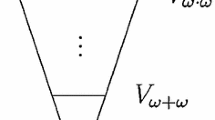
\(\hbox {V}_{\mathrm{2w}}\) is a cumulative hierarchy of sets in the von Neumann universe of sets of a certain size. The axioms of Zermelo set theory can be interpreted as ranging over the sets in this model. This resulting system is powerful enough to provide models of almost all ordinary mathematics.
The problem is analogous to intuitionistic attempts at a re-construal of natural mathematics. It is difficult to maintain that only a small part of natural mathematics is valid, or similarly that only a small part of mathematics is about real objects.
We have discussed some reasons why the full axiomatization corresponding to ZFC set theory would be preferable but the reasons why are only loosely associated with empirical evidence. The matter is not entirely conceptual however because given a broad understanding of empirics we can treat our observations of the practices of mathematicians as empirical evidence. There exists a group of people (mathematicians) engaged in a type of activity (natural mathematics) and the best explanation of what is going on requires us to propose the present full axiomatization. It just happens that only part of this axiomatization can be further supported by the more traditionally empirical evidence to be discussed in Sect. 3.
This is important to emphasize, as the TSM is not a theory in physics, and should not be evaluated in the same way that theories in physics are evaluated. Just as we would not require the theory of evolution to make the same types of predictions as quantum mechanics, so too should we not require the TSM to make predictions of the sort that are typical in physics or any other existing branch of science.
The Self-Model Theory of Subjectivity provides a good summary of such a system. It also provides a useful framework for deriving the phenomenal appearances of subjectivity, temporality, and materialism, even if the substrate for such a system is purely structural. Several intuitive objections to the TSM are responded to by reference to the SMT. See Metzinger (2003).
Noteworthy is the notion of causation is displaced as a primitive in our conceptual scheme. The dynamics do not cause any state of reality to change. They merely describe, over a certain domain, how one state of reality is related to adjacent ones. One state of reality does not come into being in virtue of its generation from another state of reality over time. The states are merely related by the dynamics. It is analogous to how the derivative of a function can describe how values of that function relate to each other, but the derivative is not causal in any metaphysical sense. The concept of causation is only useful when describing the time evolution of states of reality within a universe over some time continuous domain, just as the concept of a derivative is only useful when describing the changes of a function over some differentiable domain. There is no problem accepting functions that begin out of nowhere as it were, just as there is no problem with physical realities that have a beginning or an end in time.
It is true that a modified effective laws of physics might give rise to another type of observer, but the assumption that life requires galaxy formation should nonetheless be unproblematic.
See Ladyman and Ross (2009) for a good summary of the research in this area and an argument in favor of ontic physical structuralism, an idea related to the MUH but motivated and organized along different lines. The arguments in favor of OSR may for the most part also be viewed as arguments for the TSM. A further discussion of physical structuralism can be found in Bokulich and Bokulich (2011).
Mathematical realism in ontology is an old idea sometimes called Platonism. Most practicing mathematicians and many physicists and philosophers of mathematics accept some form of mathematical realism.
The existential significance of mathematical objectivity was emphasized by Georg Kreisel, to whom the dictum is attributed: ‘the point is not the existence of mathematical objects, but the objectivity of mathematical truth’. Roger Penrose has more recently emphasized the role of mathematical objectivity in existential explanations.
There is something of a MUH continuum that restricts the structural multiverse in various ways. A possible variation could be to limit the universes to only computable ones (CUH), or to those with finite positions (FUH).
Scientific Metaphysics edited by Ross et al. (2013) outlines several different interpretations of the scope, purpose and possibility of a naturalized metaphysics.
References
Bokulich, A., & Bokulich, P. (2011). Scientific structuralism. Berlin: Springer.
Bostrom, N. (2010). Anthropic bias: Observation selection effects in science and philosophy. London: Routledge.
Ladyman, J., & Ross, D. (2009). Every thing must go. Oxford: Oxford University Press.
Metzinger, T. (2003). Being no one: The self-model theory of subjectivity. Cambridge, MA: MIT Press.
Resnik, M. (1997). Mathematics as a science of patterns. Oxford: Clarendon Press.
Ross, D., Ladyman, J., & Kincaid, H. (2013). Scientific metaphysics. Oxford: Oxford University Press.
Shapiro, S. (1994). Foundations without foundationalism: A case for second-order logic. Oxford: Clarendon Press.
Shapiro, S. (1997). The philosophy of mathematics: Structure and ontology. Oxford: Oxford University Press.
Steiner, M. (2002). The applicability of mathematics as a philosophical problem. Cambridge, MA: Harvard University Press.
Tegmark, M. (1998). Is the ‘theory of everything’ merely the ultimate ensemble theory? Annals of Physics, 270, 1–51.
Tegmark, M. (2008). The mathematical universe. Foundations of Physics, 38, 101–150.
Tegmark, M. (2013). Our mathematical universe: My personal quest for the ultimate nature of reality. New York: Knopf Publishing Group.
Van Fraassen, B. C. (1980). The scientific image. Oxford: Clarendon Press.
Vilenkin, A. (2007). Many worlds in one. Atlanta, GA: FSG Adult.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hamlin, C. Towards a theory of universes: structure theory and the mathematical universe hypothesis. Synthese 194, 571–591 (2017). https://doi.org/10.1007/s11229-015-0959-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-015-0959-y