Abstract
Two of the major problems in AGM-style belief revision, namely the difficulties in accounting for iterated change and for Ramsey test conditionals, have satisfactory solutions in descriptor revision. In descriptor revision, the input is a (set of) metalinguistic sentence(s) specifying the success condition of the operation. The choice mechanism selects one of the potential outcomes (available belief sets) in which the success condition is satisfied. Iteration of this operation is unproblematic. Ramsey test conditionals can be introduced without giving rise to the paradoxical results that they generate in other systems. In addition to standard (sentential) Ramsey test conditionals, a more general variant of epistemic conditionals is defined, representing statements of the form ”if the belief state is changed to satisfy condition A then it will satisfy condition B”. An axiomatic characterization of such descriptor conditionals is presented. It is related in intricate ways to the KLM postulates for cumulative reasoning.


Similar content being viewed by others
Notes
In AGM theory, for any sentence p, the belief set Cn(K ∪ {p}) is obtainable from the original belief set K by revision either by p or by falsum. See Hansson [14] for a discussion of the problems that this multiplicity of outcomes gives rise to.
A set \(\mathbb {Y}\) of belief sets is descriptor-definable if and only if there is some descriptor Ψ such that for all belief sets Y : \(Y \in \mathbb {Y}\) if and only if \(Y \Vdash {\Psi }\). A relation ≦ on a set \(\mathbb {X}\) of belief sets is descriptor-wellfounded if and only if each non-empty descriptor-definable subset of \(\mathbb {X}\) has a ≦-minimal element [21].
This postulate differs from that of (local) regularity used in Hansson [21] (If \(X \circ {\Xi } \Vdash {\Psi }\) then \(X \circ {\Psi } \Vdash {\Psi }\)). The global variant ensures that the outcome set is the same independently of which element of \(\mathbb {X}\) we apply ∘ to.
Properties of binary relations are transferred to ternary relations by keeping the middle term constant.
The property of weak connectedness was used (under the same name) in a decision-theoretical framework by Fishburn [9, p.11].
As can be seen from the proof, weak connectedness holds essentially because for any two belief sets X and Z there is a descriptor Ψ that is satisfied by X and Z, but not by any other belief set. Then Y∘Ψ must be either X or Z, and consequently one of them must block the other from the standpoint of Y .
The term “pseudodistance” has been used since the 19 th century for various weakenings of, and alternatives to, standard Euclidean distance. It is used here to denote a weakening of the standard concept of a distance, such that δ(X,Y)=δ(Y,X) does not hold in general. See Lehmann et al. [29, p. 300] for a useful general definition of pseudodistances in this sense.
Negative transmission is related with the symmetry requirement of (V +), as can be seen from the fact that negative transmission holds if there is some real-valued measure such that δ(X,Y)=δ(Y,X) for all X and Y and that
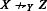 if and only if δ(X,Y)≤δ(Y,Z). Negative transmission is also closely related to an axiom introduced under the name “loop” by Lehmann et al. [29], p. 306. To see the connection with “loop”, note that Lehmann et al refer to distances between sets of objects. In their notation, X ∣ Y is the set of elements y of Y such that min
x∈X
δ(x,y) is at least as small as is min
x∈X
δ(x,y
′) for any other element y
′ of Y . Therefore their formula \((X_{1}\mid (X_{0}\cup X_{2}))\cap X_{0} \neq \varnothing \) can be interpreted in the singleton case (X
0 = {x
0}, X
1 = {x
1}, and X
2 = {x
2}) as saying that x
0 is at least as close to x
1 as it is to x
2.
if and only if δ(X,Y)≤δ(Y,Z). Negative transmission is also closely related to an axiom introduced under the name “loop” by Lehmann et al. [29], p. 306. To see the connection with “loop”, note that Lehmann et al refer to distances between sets of objects. In their notation, X ∣ Y is the set of elements y of Y such that min
x∈X
δ(x,y) is at least as small as is min
x∈X
δ(x,y
′) for any other element y
′ of Y . Therefore their formula \((X_{1}\mid (X_{0}\cup X_{2}))\cap X_{0} \neq \varnothing \) can be interpreted in the singleton case (X
0 = {x
0}, X
1 = {x
1}, and X
2 = {x
2}) as saying that x
0 is at least as close to x
1 as it is to x
2.Frank Ramsey [35, p. 247] noted that “[i]f two people are arguing ‘If p will q?’ and are both in doubt as to p, they are adding p hypothetically to their stock of knowledge and are arguing on that basis about q.” Robert Stalnaker [40, pp. 101–105] developed this proposal into a general principle. See Hansson [14] for a defence of the Ramsey test.
Ex falso quodlibet is usually not mentioned in presentations of conditional logic, but it follows from the common principle that α → β holds whenever α logically implies β. See e.g. Burgess [4].
Technically, in the logic of descriptors a belief set X is interchangeable with a descriptor π X that is satisfied by X but not by any other belief set. (See Definition 5.) Therefore unitarity can equivalently be expressed by a requirement that the descriptor {Ξ∣Ψ ⇒ Ξ} is satisfied by exactly one belief set; this is also why the name “unitarity” was chosen for this postulate.
The And postulate follows from the other five, see Kraus et al 1990, p. 179.
As shown in Hansson [22], \(X \Vdash {\Psi } \veebar {\Xi }\) holds if and only if either \(X \Vdash {\Psi }\) or \(X \Vdash {\Xi }\) holds.
To show that \(\trianglelefteq ^\#\) is well-defined it is sufficient to show that if \(\{X,Y\} \underline {\vartriangle }^{\ast } \{X^{\prime },Y^{\prime }\}\) and \(\{X,Z\} \underline {\vartriangle }^{\ast } \{X^{\prime },Z^{\prime }\} \), then \(\{X,Y\} \trianglelefteq ^{\ast }\{X,Z\}\) iff \(\{X^{\prime },Y^{\prime }\} \trianglelefteq ^{\ast }\{X^{\prime },Z^{\prime }\}\). Let \(\{X,Y\} \underline {\vartriangle }^{\ast } \{X^{\prime },Y^{\prime }\} \), \(\{X,Z\} \underline {\vartriangle }^{\ast } \{X^{\prime },Z^{\prime }\} \), and \(\{X,Y\} \trianglelefteq ^{\ast }\{X,Z\}\). It follows from \(\{X,Y\} \underline {\vartriangle }^{\ast } \{X^{\prime },Y^{\prime }\} \) that \(\{X^{\prime },Y^{\prime }\} \trianglelefteq ^{\ast }\{X,Y\}\) and from \(\{X,Z\} \underline {\vartriangle }^{\ast } \{X^{\prime },Z^{\prime }\} \) that \(\{X,Z\} \trianglelefteq ^{\ast }\{X^{\prime },Z^{\prime }\}\). Using \(\{X,Y\} \trianglelefteq ^{\ast }\{X,Z\}\) and the transitivity of \(\trianglelefteq ^{\ast }\) we obtain \(\{X^{\prime },Y^{\prime }\} \trianglelefteq ^{\ast }\{X^{\prime },Z^{\prime }\}\).
Note that {X, X}≈{Y, Y} yields δ ′(⌊{X, X}⌋) = δ ′(⌊{Y, Y}⌋).
Note that through the Lemma, negative transmission is used at this point.
References
Alchourrón, C., Gärdenfors, P., & Makinson, D. (1985). On the logic of theory change: partial meet contraction and revision functions. Journal of Symbolic Logic, 50, 510–530.
Alchourrón, C., & Makinson, D. (1982). On the logic of theory change: contraction functions and their associated revision functions. Theoria, 48, 14–37.
Bezzazi, H., Makinson, D., & Pino Pérez, R. (1997). Beyond rational monotony: some strong non-Horn conditions for nonmonotonic inference operations. Journal of Logic and Computation, 7, 605–631.
Burgess, J.P. (1981). Quick completeness proofs for some logics of conditionals. Notre Dame Journal of Formal Logic, 22, 76–84.
Darwiche, A., & Pearl, J. (1997). On the logic of iterated belief revision. Journal of Artificial Intelligence, 89, 1–29.
Edgington, D. (2007). On conditionals. In D.M. Gabbay, & F. Guenthner (Eds.), Handbook of philosophical logic. 2nd edn., (Vol. 14 pp. 127–221). Dordrecht: Springer.
Fermé, E., & Hansson, S.O. (2001). Shielded Contraction. In H. Rott, & M.-A. Williams (Eds.), Frontiers of belief revision (pp. 85–107): Kluwer 2001.
Fermé, E., & Hansson, S.O. (2011). AGM 25 years. Twenty-Five years of research in belief change. Journal of Philosophical Logic, 40, 295–331.
Fishburn, P.C. (1970). Utility theory for decision making. New York: Wiley.
Galliers, J.R. (1992). Autonomous belief revision and communication. In P. Gärdenfors (Ed.), Belief revision (pp. 220–246). Cambridge: Cambridge University Press.
Gärdenfors, P. (1986). Belief revisions and the Ramsey test for conditionals. Philosophical Review, 95, 81–93.
Gärdenfors, P., & Makinson, D. (1988). Revisions of knowledge systems using epistemic entrenchment. In M.Y. Vardi (Ed.), Proceedings of the 2nd conference on theoretical aspects of reasoning about knowledge (pp. 83–95). Los Altos: Morgan Kaufmann.
Hansson, S.O. (1991). Belief contraction without recovery. Studia Logica, 50, 251–260.
Hansson, S.O. (1992). In defense of the Ramsey test. Journal of Philosophy, 89, 522–540.
Hansson, S.O. (1999). A textbook of belief dynamics. Dordrecht: Kluwer.
Hansson, S.O. (2001). Preference logic. In D. Gabbay, & F. Guenthner (Eds.), Handbook of philosophical logic. 2nd edn. (pp. 319–393).
Hansson, S.O. (2008). Specified meet contraction. Erkenntnis, 69, 31–54.
Hansson, S.O. (2013). Cognitive realism in belief revision. In E.Fermé, & G. Simari (Eds.), Trends in belief revision and argumentation dynamics (pp. 57–74). London: College Publications.
Hansson, S.O. (2013). Blockage contraction. Journal of Philosophical Logic, 42, 415–442.
Hansson, S.O. (2013). Outcome level analysis of belief contraction. Review of Symbolic Logic, 6, 183–204.
Hansson, S.O. (2014). Descriptor revision. Studia Logica, 102, 955–980.
Hansson, S.O. (2014). Relations of epistemic proximity for belief change. Artificial Intelligence, 217, 76–91.
Hansson, S.O., Fermé, E., Cantwell, J., & Falappa, M. (2001). Credibility-limited revision. Journal of Symbolic Logic, 66, 1581–1596.
Jech, T.J. ([1973] 2008). The axiom of choice. Mineola, N.Y.: Dover Publications.
Jin, Y., & Thielscher, M. (2007). Iterated belief revision, revised. Artificial Intelligence, 171, 1–18.
Konieczny, S., & Pino Pérez, R. (2000). A framework for iterated revision. Journal of Applied Non-classical logics, 10, 339–367.
Kraus, S., Lehmann, D., & Magidor, M. (1990). Nonmonotonic reasoning, preferential models and cumulative logics. Artificial Intelligence, 44, 167–207.
Lehmann, D. (1995). Belief revision, revised. In Proceedings of the 14th international joint conference on artificial intelligence (IJCAI-95) (pp. 1534–1540).
Lehmann, D., Magidor, M., & Schlechta, K. (2001). Distance semantics for belief revision. Journal of Symbolic Logic, 66, 295–317.
Lindström, S., & Rabinowicz, W. (1991). Epistemic entrenchment with incomparabilities and relational belief revision. In A. Fuhrmann, & M. Morreau (Eds.), The logic of theory change (p. 93126). New York: Springer.
Lindström, S., & Rabinowicz, W. (1992). Belief revision, epistemic conditionals and the Ramsey test. Synthese, 91, 195–237.
Makinson, D. (1994). General patterns in nonmonotonic reasoning. In D.M. Gabbay, C.J. Hogger, & J.A. Robinson (Eds.), Handbook of logic in artificial intelligence and logic programming, Nonmonotonic reasoning and uncertain reasoning, (Vol. 3 pp. 35–110). Oxford: Clarendon.
Makinson, D. (1997). Screened revision. Theoria, 63, 14–23.
Peppas, P. (2014). A panorama of iterated revision. In S.O. Hansson (Ed.), David Makinson on classical methods for non-classical problems (pp. 71–94). Dordrecht: Springer.
Ramsey, F. (1931). Foundations of mathematics and other logical essays. New York: Routledge.
Roberts, F.S. (1979). Measurement theory with applications to decisionmaking, utility and the social sciences. Reading: Addison-Wesley.
Rott, H. (1999). Moody conditionals: Hamburgers, switches, and the tragic death of an American president. In J. Gerbrandy, M. Marx, M. de Rijke, & Y. Venema (Eds.), Essays dedicated to Johan van Benthem on the occasion of his 50th birthday. http://www.illc.uva.nl/j50/contribs/rott (pp. 98–112). Amsterdam: Amsterdam University Press.
Rott, H. (2001). Change, choice and inference: a study of belief revision and nonmonotonic reasoning. Oxford: Oxford University Press.
Rott, H. (2009). Shifting priorities: simple representations for twenty-seven iterated theory change operators. In D. Makinson, J. Malinowski, & H. Wansing (Eds.), Towards Mathematical Philosophy. Papers from the Studia Logica conference Trends in Logic IV. Springer (pp. 269–296).
Stalnaker, R. (1968). A theory of conditionals. In N. Rescher (Ed.), Studies in logical theory, american philosophical quarterly monograph series, II (pp. 98–112). Cambridge: Blackwell.
Stalnaker, R. (2009). Iterated belief revision. Erkenntnis, 70, 189–209.
Ullmann-Margalit, E., & Morgenbesser, S. (1977). Picking and choosing. Social Research, 44, 757–78.
Acknowledgment
I would like to thank John Cantwell for a series of conversations on the logic of conditionals that were unusually helpful in the preparation of this paper.
Author information
Authors and Affiliations
Corresponding author
Appendix: Proofs
Appendix: Proofs
Definition 5
[22]
-
(i)
\({\Pi }_{X} = \{\mathfrak {B}p \mid p \in X\} \cup \{\neg \mathfrak {B}p \mid p \notin X\}\)
-
(ii)
\({\Psi }_{1} \veebar {\Psi }_{2} = \{\alpha \vee \beta \mid (\alpha \in {\Psi }_{1}) \ \& \ (\beta \in {\Psi }_{2})\}\)
Lemma 1
Let ∘ be a global operation on the elements of a set \(\mathbb {X}\) of belief sets, with descriptors as inputs and elements of \(\mathbb {X}\) as outputs. Let \(X, Y_{1}, {\dots } , Y_{n} \in \mathbb {X}\) . If ∘ satisfies global regularity and either confirmation or relative success, then \(X\circ ({\Pi }_{Y_{1}} \veebar {\dots } \veebar {\Pi }_{Y_{n}}) ~\in \ \{Y_{1}, {\dots } , Y_{n}\}\).
Proof of Lemma 1
Since \(Y_{1} \Vdash {\Pi }_{Y_{1}}\) we obtain \(Y_{1} \circ {\Pi }_{Y_{1}} \Vdash {\Pi }_{Y_{1}}\) from either confirmation or relative success. It follows that \(Y_{1} \circ {\Pi }_{Y_{1}} \Vdash {\Pi }_{Y_{1}}\veebar {\dots } \veebar {\Pi }_{Y_{n}}\), global regularity yields \(X\circ ({\Pi }_{Y_{1}} \veebar {\dots } \veebar {\Pi }_{Y_{n}})\Vdash {\Pi }_{Y_{1}} \veebar {\dots } \veebar {\Pi }_{Y_{n}}\) and we can use the observation referred to in footnote 13 to obtain \(X\circ ({\Pi }_{Y_{1}} \veebar {\dots } \veebar {\Pi }_{Y_{n}}) \ \in \ \{Y_{1}, {\dots } , Y_{n}\}\). □
Lemma 2
-
(1)
If a relation \(\rightharpoondown \) satisfies asymmetry, then it satisfies irreflexivity.
-
(2)
If a relation \(\rightharpoondown \) satisfies transitivity and irreflexivity, then it satisfies asymmetry.
Proof of Lemma 2
Part 1: Directly by substitution.
Part 2: Let \(\rightharpoondown \) be transitive and irreflexive, and suppose for contradiction that it is not asymmetric. Then there are Y and Z such that \(Y\rightharpoondown Z\) and \(Z\rightharpoondown Y\). Transitivity yields \(Y\rightharpoondown Y\), contrary to irreflexivity. □
Lemma 3
Let \(\rightharpoondown _{X}\) be a transitive and irreflexive relation, and let \(\bar {\rightharpoondown }_{X}\) be the relation such that \(Y \bar {\rightharpoondown }_{X} Z\) iff either \(Y\rightharpoondown _{X} Z\) or Y=Z. Then \(\bar {\rightharpoondown }_{X}\) is transitive, reflexive, and antisymmetric.
Proof of Lemma 3
Reflexivity follows from the reflexivity of identity. For transitivity, note that if \(Y\bar {\rightharpoondown }_{X} Z ~\& Z \bar {\rightharpoondown }_{X} V\), then there are four possibilities, namely \(Y\rightharpoondown _{X} Z~ \& ~ Z \rightharpoondown _{X} V\), \(Y = Z ~ \& ~ Z \rightharpoondown _{X} V\), \(Y\rightharpoondown _{X} Z ~ \& ~ Z = V\), and Y = Z & Z = V. In the first case \(Y \rightharpoondown _{X} V\) and thus \(Y \bar {\rightharpoondown }_{X} V\) follow from the transitivity of \(\rightharpoondown \), and in the following two cases from substitution of identicals. In the forth case \(Y \bar {\rightharpoondown }_{X} V\) follows from the transitivity of identity. For antisymmetry, let \(Y \bar {\rightharpoondown }_{X} Z\) and \(Z \bar {\rightharpoondown }_{X} Y\). If follows from the definition of \(\bar {\rightharpoondown }\) that either Y = Z or \(Y \rightharpoondown _{X} Z ~\& ~ Z \rightharpoondown _{X} Y\). The latter is impossible due to the asymmetry of \(\rightharpoondown \) that follows from Lemma 2. Thus Y = Z. □
Lemma 4
Let \(\rightharpoondown \) be a ternary relation that satisfies asymmetry and weak connectedness, and \(\bar {\rightharpoondown }\) the relation such that \(X \bar {\rightharpoondown }_{Y} Z\) iff either \(X\rightharpoondown _{Y} Z\) or X=Z. Then:
-
(1)
It holds for all X, Y, and Z that \(X \bar {\rightharpoondown }_{Y} Z\) iff .
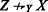
-
(2)
If \(\rightharpoondown \) satisfies negative transmission, then \(\bar {\rightharpoondown }\) satisfies:
If \(X_{1} \bar {\rightharpoondown }_{X_{2}}X_{3}, \ X_{2} \bar {\rightharpoondown }_{X_{3}}X_{4}, {\dots } , X_{n-2} \bar {\rightharpoondown }_{X_{n-1}}X_{n}\) , and X 2 =X n−1 , then \(X_{1} \bar {\rightharpoondown }_{X_{2}}X_{n}\).
Proof of Lemma 4
Part 1: First let \(X \bar {\rightharpoondown }_{Y} Z\), i.e. either \(X\rightharpoondown _{Y} Z\) or X = Z. In the former case  follows from the asymmetry of \(\rightharpoondown \) and in the latter case from its irreflexivity that follows from its asymmetry (Lemma 2). Next let
follows from the asymmetry of \(\rightharpoondown \) and in the latter case from its irreflexivity that follows from its asymmetry (Lemma 2). Next let  . It follows from weak connectedness that either \(X\rightharpoondown _{Y} Z\) or X = Z, i.e. \(X \bar {\rightharpoondown }_{Y} Z\).
. It follows from weak connectedness that either \(X\rightharpoondown _{Y} Z\) or X = Z, i.e. \(X \bar {\rightharpoondown }_{Y} Z\).
Part 2: Consider the following substitution instance of negative transmission:
If
,
, …,
,
and X 2 = X n−1, then
.
According to part 1 it is equivalent with
If \(X_{n-2} \bar {\rightharpoondown }_{X_{n-1}} X_{n}, \ X_{n-3} \bar {\rightharpoondown }_{X_{n-2}} X_{n-1}, {\dots } , X_{2} \bar {\rightharpoondown }_{X_{3}}X_{4}\),
and X 2 = X n−1, then \(X_{1} \bar {\rightharpoondown }_{X_{2}}X_{n}\).
as desired. □
Lemma 5
Let ∘ be a descriptor revision. If it satisfies relative success, global regularity, and cumulativity, then it satisfies:
-
If \(X\circ {\Xi }\Vdash {\Psi }\) iff \(X\circ {\Xi }\Vdash {\Psi }^{\prime }\) for all Ξ, then X∘Ψ=X∘Ψ ′ (uniformity)
Proof of Lemma 5
Let Ψ and Ψ′ be descriptors such that \(K\circ {\Xi }\Vdash {\Psi }\) iff \(K\circ {\Xi }\Vdash {\Psi }^{\prime }\) for all Ξ.
Case 1, there is no Ξ such that \(X\circ {\Xi }\Vdash {\Psi }\): Then by supposition there is no Ξ such that \(X\circ {\Xi }\Vdash {\Psi }^{\prime }\). It follows from relative success that X ∘ Ψ = X and X ∘ Ψ′ = K.
Case 2, there is some Ξ′ such that \(X\circ {\Xi }^{\prime }\Vdash {\Psi }\): Then by the assumption \(X\circ {\Xi }^{\prime }\Vdash {\Psi }^{\prime }\). Due to global regularity it follows from \(X\circ {\Xi }^{\prime }\Vdash {\Psi }\) that \(X\circ {\Psi }\Vdash {\Psi }\) and from \(X\circ {\Xi }^{\prime }\Vdash {\Psi }^{\prime }\) that \(X\circ {\Psi }^{\prime }\Vdash {\Psi }^{\prime }\). Due to our assumption (substituting Ψ for Ξ) we can conclude from \(X\circ {\Psi }\Vdash {\Psi }\) that \(X\circ {\Psi }\Vdash {\Psi }^{\prime }\). Similarly (substituting Ψ′ for Ξ) we can conclude from \(X\circ {\Psi }^{\prime }\Vdash {\Psi }^{\prime }\) that \(X\circ {\Psi }^{\prime }\Vdash {\Psi }\). Applying cumulativity to \(X\circ {\Psi }\Vdash {\Psi }^{\prime }\) we obtain X ∘ Ψ = X∘(Ψ∪Ψ′), and applying the same postulate to \(X\circ {\Psi }^{\prime }\Vdash {\Psi }\) we obtain X ∘ Ψ′ = X∘(Ψ∪Ψ′). Thus X ∘ Ψ = X ∘ Ψ′ in this case as well. □
Proof of Theorem 1
The equivalence between (I), (II), and (III) follows directly from the corresponding proof for local descriptor revision in [21] and Lemma 5.
From (III) to (IV): Weak connectedness: Let X ≠ Z and \(X, Y, Z \in \mathbb {X}\). It follows from relative success, global regularity and Lemma 1 that \(Y\circ ({\Pi }_{X} \veebar {\Pi }_{Z}) \ \in \ \{X, Z\}\). Without loss of generality we can assume that \(Y\circ ({\Pi }_{X} \veebar {\Pi }_{Z}) = X\). In order to show that \(X \rightharpoondown _{Y} Z\), suppose to the contrary that there is some Ψ such that \(X\Vdash {\Psi }\) and Y ∘ Ψ = Z. Then \(Y\circ {\Psi } \Vdash {\Pi }_{Z}\), thus \(Y\circ {\Psi } \Vdash {\Pi }_{X} \veebar {\Pi }_{Z}\). Due to cumulativity, \(Y\circ {\Psi } = Y\circ ({\Psi }\cup ({\Pi }_{X} \veebar {\Pi }_{Z}))\). Due to confirmation, X∘π X = X, thus \(X \circ {\Pi }_{X} \Vdash {\Psi }\), and since Y ∘ Ψ = Z it follows from global regularity that \(Z\Vdash {\Psi }\), and we can conclude from \(X\Vdash {\Psi }\) and \(Z\Vdash {\Psi }\) that \({\Pi }_{X}\veebar {\Pi }_{Z}\Vdash {\Psi }\), thus \({\Pi }_{X}\veebar {\Pi }_{Z} \dashv \Vdash {\Psi }\cup ({\Pi }_{X}\veebar {\Pi }_{Z})\). Uniformity that we have from Lemma 5 yields \(Y\circ ({\Pi }_{X}\veebar {\Pi }_{Z})= Y\circ ({\Psi } \cup ({\Pi }_{X}\veebar {\Pi }_{Z}))\). We now have \(X = Y\circ ({\Pi }_{X} \veebar {\Pi }_{Z}) = Y\circ ({\Psi } \cup ({\Pi }_{X}\veebar {\Pi }_{Z})) = Y\circ {\Psi } =Z\), contrary to X ≠ Z. We can conclude from this contradiction that \(X\rightharpoondown _{Y} Z\).
Irreflexivity: Suppose to the contrary that \(X\rightharpoondown _{Y} X\). It follows from relative success, global regularity, and Lemma 1 that Y∘π X = X, but that is impossible since \(X\rightharpoondown _{Y} X\).
Transitivity: Let \(X\rightharpoondown _{V} Y\) and \(Y \rightharpoondown _{V} Z\). Due to asymmetry that we have just shown, X ≠ Z. Due to weak connectedness that we have also shown, either \(X\rightharpoondown _{V} Z\) or \(Z \rightharpoondown _{V} X\). Suppose that \(Z\rightharpoondown _{V} X\). We have X∘π
X
= X from confirmation, thus \(X\circ {\Pi }_{X} \Vdash {\Pi }_{X}\veebar {\Pi }_{Y}\veebar {\Pi }_{Z}\), and global regularity yields \(V\circ ({\Pi }_{X}\veebar {\Pi }_{Y}\veebar {\Pi }_{Z}) \Vdash {\Pi }_{X}\veebar {\Pi }_{Y}\veebar {\Pi }_{Z}\), thus due to Lemma 1, \(V\circ ({\Pi }_{X}\veebar {\Pi }_{Y}\veebar {\Pi }_{Z}) ~\in ~ \{X,Y,Z\}\). However this is impossible since \(X\rightharpoondown _{V} Y\), \(Y\rightharpoondown _{V} Z\), and \(Z \rightharpoondown _{V} X\). We can conclude from this contradiction that  , thus \(X\rightharpoondown _{V} Z\) as desired.
, thus \(X\rightharpoondown _{V} Z\) as desired.
Superiority: Let X ≠ Y. Confirmation yields \(X\circ ({\Pi }_{X}\veebar {\Pi }_{Y}) = X\). It follows from \(Y \Vdash {\Pi }_{X}\veebar {\Pi }_{Y}\) that  , thus due to weak connectedness that we have just shown, \(X\rightharpoondown _{X} Y\).
, thus due to weak connectedness that we have just shown, \(X\rightharpoondown _{X} Y\).
The connection between ◦ and ⇁ : If \(\mathbb {X}\) has some element Y that satisfies Ψ then we can use confirmation to obtain \(Y\circ {\Pi }_{Y}\Vdash {\Psi }\) and then global regularity to obtain \(X\circ {\Psi }\Vdash {\Psi }\). Due to Definition 1 and the weak connectedness of \(\rightharpoondown \) that was shown above, X ∘ Ψ is then the unique \(\rightharpoondown _{X}\)-unblocked element among the set of Ψ-satisfying elements of \(\mathbb {X}\). If \(\mathbb {X}\) has no Ψ-satisfying element, then \(X \circ {\Psi } \nVdash {\Psi }\), and it follows from relative success that X ∘ Ψ = X.
From (IV) to (III): Closure, confirmation, relative success, and global regularity all follow directly from the definitions.
Cumulativity: Let \(X\circ {\Psi }\Vdash {\Xi }\). If \(X\circ {\Psi } \nVdash {\Psi }\), then due to (IV) \(\mathbb {X}\) has no Ψ-satisfying element, thus it has no Ψ∪Ξ-satisfying element, and (IV) directly yields X ∘ Ψ = X and X∘(Ψ∪Ξ) = X. If \(X\circ {\Psi } \Vdash {\Psi }\), then X ∘ Ψ is a Ψ∪Ξ-satisfying element of \(\mathbb {X}\). Since the Ψ∪Ξ-satisfying elements form a subset of the Ψ-satisfying elements, and \((X\circ {\Psi }) \rightharpoondown _{X} Y\) for all elements Y of the latter set except X ∘ Ψ itself, we can conclude that \((X\circ {\Psi }) \rightharpoondown _{X} Y\) for all Ψ ∪ Ξ-satisfying elements Y of \(\mathbb {X}\), except X ∘ Ψ itself. Thus X ∘ Ψ = X∘(Ψ∪Ξ).
From (IV) to (V) when \(\mathbb {X}\) is countable: Due to Cantor’s representation theorem for countable sets [36, pp. 109–111], if \(\mathbb {X}\) is countable then there is some real-valued measure d Y such that d Y (X) ≤ d Y (Z) iff \(X \bar {\rightharpoondown }_{Y} Z\). Let δ be the real-valued measure such that δ(Y, X) = d Y (X)−d Y (Y) for all \(X, Y \in \mathbb {X}\).
From (V) to (IV): Let \(X \rightharpoondown _{Y} Z\) iff δ(Y, X)<δ(Y, Z).
For transitivity, let \(X\rightharpoondown _{V} Y\) and \(Y\rightharpoondown _{V} Z\). Then δ(V, X)<δ(V, Y) and δ(V, Y)<δ(V, Z), thus δ(V, X)<δ(V, Z), thus \(X\rightharpoondown _{V} Z\).
For weak connectedness, let X ≠ Z. It follows from the properties of δ that δ(Y, X) ≠ δ(Y, Z), thus either δ(Y, X)<δ(Y, Z) or δ(Y, Z)<δ(Y, X), thus either \(X \rightharpoondown _{Y} Z\) or \(Z \rightharpoondown _{Y} X\).
For irreflexivity, note that \(X \rightharpoondown _{Y} X\) would imply δ(Y, X)<δ(Y, X).
For superiority, let X ≠ Y. Then δ(X, X) = 0 and δ(X, Y) ≠ 0, thus δ(X, X)<δ(X, Y), thus \(X\rightharpoondown _{X} Y\).
Proof of Theorem 2
From (IV + ) to (V + ): We are going to construct a measure δ and then verify that for all \(X \in \mathbb {X}\) it relates to \(\rightharpoondown _{X}\) in the desired way.
For the construction, let \(\bar {\rightharpoondown }\) be the relation on the elements of \(\mathbb {X}\) such that \(X \bar {\rightharpoondown }_{Y} Z\) iff either \(X\rightharpoondown _{Y} Z\) or X = Z. Due to Lemma 3, for all X, \(\bar {\rightharpoondown }_{X}\) is transitive, reflexive, and antisymmetric. For each \(X \in \mathbb {X}\) we introduce the relation \(\trianglelefteq _{X}\) on subsets of \(\mathbb {X}\) containing X and at most one additional element, such that for all \(Y, Z \in \mathbb {X}\):
Since there is a one-to-one correspondence between the sets eligible as arguments of \(\trianglelefteq _{X}\) and the elements of \(\mathbb {X}\), it follows from the transitivity, reflexivity, and antisymmetry of \(\bar {\rightharpoondown }_{X}\) that \(\trianglelefteq _{X}\) is also transitive, reflexive, and antisymmetric. Let ≈ be the relation such that {X, Y}≈{Z, V} iff X = Y and Z = V. Construct the union of ≈ and all the relations \(\trianglelefteq _{X}\) for \(X\in \mathbb {X}\). The transitive closure of this union is denoted \(\trianglelefteq ^{\ast }\). Its domain consists of all subsets of \(\mathbb {X}\) with either one or two elements. Let \(\underline {\vartriangle }^{\ast }\) be the symmetrical part of \(\trianglelefteq ^{\ast }\), i.e. \(\{X,Y\} \underline {\vartriangle }^{\ast } \{Z,V\}\) iff \(\{X,Y\} \trianglelefteq ^{\ast } \{Z,V\} \trianglelefteq ^{\ast } \{X,Y\}\). Since \(\trianglelefteq ^{\ast }\) is transitive and reflexive, \(\underline {\vartriangle }^{\ast }\) is transitive, symmetric, and reflexive, i.e. an equivalence relation. For each set {X, Y} of one or two elements of \(\mathbb {X}\), let ⌊{X, Y}⌋ be its equivalence class under \(\underline {\vartriangle }^{\ast }\). Let \(\trianglelefteq ^\#\) be the relation on these equivalence classes such that \(\lfloor \{X,Y\} \rfloor \trianglelefteq ^\# \lfloor \{X,Z\} \rfloor \) if and only if \(\{X,Y\} \trianglelefteq ^{\ast } \{X,Z\}\).Footnote 14 It follows directly that \(\trianglelefteq ^\#\) is transitive, reflexive, and antisymmetric, i.e. a partial order. (\(\trianglelefteq ^\#\) is the reduction of \(\trianglelefteq ^{\ast }\), cf. Roberts [36], pp. 30–31.)
Due to the order extension principle (that follows from the axiom of choice, Jech [24], p. 19) there is a total order (transitive, complete, and antisymmetric relation) \(\trianglelefteq ^{\ddagger }\) that extends \(\trianglelefteq ^\#\). Due to Cantor’s representation theorem for countable sets [36, pp. 109–111] there is a real-valued function δ ′ such that \(\lfloor \{X,Y\} \rfloor \trianglelefteq ^{\ddagger } \lfloor \{Z,V\} \rfloor \) iff δ ′(⌊{X, Y}⌋) ≤ δ ′(⌊{Z, V}⌋). To obtain a calibrated measure, let δ(⌊{X, Y}⌋) = δ ′(⌊{X, Y}⌋)−δ ′(⌊{X, X}⌋).Footnote 15 We can apply δ also to the elements of the equivalence classes, setting δ({X, Y}) = δ(⌊{X, Y}⌋). With this our construction of a distance measure is finished.
Verification: It follows from the construction that for all \(X,Y \in \mathbb {X}\): δ(X, Y) = δ(Y, X), δ(X, X) = 0, and δ(X, Y) ≥ 0. It remains to show (A) that δ(X, Y) ≠ δ(X, Z) whenever Y ≠ Z, and (B) that if Ψ is satisfiable within \(\mathbb {X}\), then δ(X, X ∘ Ψ) ≤ δ(X, Y) whenever \(Y\Vdash {\Psi }\). The satisfaction of clause (ii) of (V +) follows directly.
Part A: We will assume that δ(X, Y) = δ(X, Z) and prove that Y = Z. If X = Y then δ(X, Y) = δ(X, X) = 0, thus δ(X, Z) = 0, thus δ ′(X, Z) = δ ′(X, X), thus \(\{X,Z\} \underline {\vartriangle }^{\ast } \{X,X\}\), thus \(Z\bar {\rightharpoondown }_{X}X\), thus X = Z. In the principal case when X ≠ Y it follows from δ(X, Y) = δ(X, Z) that \(\lfloor \{X,Y\} \rfloor \trianglelefteq ^\# \lfloor \{X,Z\} \rfloor \) and \(\lfloor \{X,Z\} \rfloor \trianglelefteq ^\# \lfloor \{X,Y\} \rfloor \).
It follows from \(\lfloor \{X,Y\} \rfloor \trianglelefteq ^\# \lfloor \{X,Z\} \rfloor \) that there is a chain of links from {X, Y} to {X, Z}, where each link has either of the forms
-
(a)
\({\dots } \{A,B\} \trianglelefteq _{B} \{B,C\}, \ \{B,C\} \trianglelefteq _{C} \{C,D\} \dots \) or
-
(b)
\({\dots } \{A,B\} \trianglelefteq _{B} \{B,C\}, \ \{B,C\} \trianglelefteq _{B} \{B,D\} \dots \)
which means equivalently that either
-
(a’)
\({\dots } A \bar {\rightharpoondown }_{B} C, \ B \bar {\rightharpoondown }_{C} D {\dots } \) or
-
(b’)
\({\dots } A \bar {\rightharpoondown }_{B} C, \ C \bar {\rightharpoondown }_{B} D \dots \)
In case (b’) we can use \(B \bar {\rightharpoondown }_{C} B\) that follows from the reflexivity of \(\bar {\rightharpoondown }\) to expand the chain as follows:
-
(b”)
\({\dots } A \bar {\rightharpoondown }_{B} C, \ B \bar {\rightharpoondown }_{C} B, \ C \bar {\rightharpoondown }_{B} D \dots \)
which means that in all cases of \(\lfloor \{X,Y\} \rfloor \trianglelefteq ^\# \lfloor \{X,Z\} \rfloor \) we have a chain of type (a’). More precisely, taking into account the beginnings and ends of these chains we have in all cases a chain of one of the four following types:
-
(1)
\(X \bar {\rightharpoondown }_{Y} S_{1}, \ Y \bar {\rightharpoondown }_{S_{1}} S_{2}, {\dots } , S_{n-1} \bar {\rightharpoondown }_{S_{n}} X, \ S_{n} \bar {\rightharpoondown }_{X} Z\)
-
(2)
\(X \bar {\rightharpoondown }_{Y} S_{1}, \ Y \bar {\rightharpoondown }_{S_{1}} S_{2}, {\dots } , S_{n-1} \bar {\rightharpoondown }_{S_{n}} Z, \ S_{n} \bar {\rightharpoondown }_{Z} X\)
-
(3)
\(Y \bar {\rightharpoondown }_{X} S_{1}, \ X \bar {\rightharpoondown }_{S_{1}} S_{2}, {\dots } , S_{n-1} \bar {\rightharpoondown }_{S_{n}} X, \ S_{n} \bar {\rightharpoondown }_{X} Z\)
-
(4)
\(Y \bar {\rightharpoondown }_{X} S_{1}, \ X \bar {\rightharpoondown }_{S_{1}} S_{2}, {\dots } , S_{n-1} \bar {\rightharpoondown }_{S_{n}} Z, \ S_{n} \bar {\rightharpoondown }_{Z} X\)
By adding \(Y \bar {\rightharpoondown }_{X} Y\) at the beginning of all chains of types 1 and 2 and \(Z \bar {\rightharpoondown }_{X} Z\) at the end of all chains of types 2 and 4 we will have in all cases a chain of type 3. It follows from Lemma 4, part 2, that \(Y \bar {\rightharpoondown }_{X} Z\), i.e. either \(Y \rightharpoondown _{X} Z\) or Y = Z.Footnote 16
Similarly, it follows from \(\lfloor \{X,Z\} \rfloor \trianglelefteq ^\# \lfloor \{X,Y\} \rfloor \) that \(Z \bar {\rightharpoondown }_{X} Y\), i.e. either \(Z \rightharpoondown _{X} Y\) or Y = Z. Since \(\rightharpoondown _{X}\) is asymmetric it follows that Y = Z.
Part B can be proved by showing that for each belief set X and each descriptor Ψ that is satisfiable within \(\mathbb {X}\), there is a unique Ψ-satisfying element of \(\mathbb {X}\) that has the smallest distance to X of all Ψ-satisfying elements of \(\mathbb {X}\). Given the result in part A we can show this by proving that \(Y \rightharpoondown _{X} Z\) iff δ(X, Y)<δ(X, Z).
For one direction, let \(Y \rightharpoondown _{X} Z\). It follows from the construction that \(\lfloor \{X,Y\} \rfloor \trianglelefteq ^\# \lfloor \{X,Z\} \rfloor \), thus δ(X, Y) ≤ δ(X, Z). It follows from the asymmetry of \(\rightharpoondown _{X}\) that Y ≠ Z and thus from part A that δ(X, Y) ≠ δ(X, Z), thus δ(X, Y)<δ(X, Z).
For the other direction, let δ(X, Y)<δ(X, Z). Then Y ≠ Z. Due to the definition of δ we also have \(\lfloor \{X,Y\} \rfloor \trianglelefteq ^\# \lfloor \{X,Z\} \rfloor \), and then it follows as in part A that \(Y \bar {\rightharpoondown }_{X} Z\). Since Y ≠ Z we can conclude that \(Y \rightharpoondown _{X} Z\), as desired.
From (V + ) to (IV +): Let \(X \rightharpoondown _{Y} Z\) iff δ(Y, X)<δ(Y, Z). The proofs of transitivity, weak connectedness, asymmetry, and superiority follow as in the proof of Theorem 1. Negative transmission can be proved as follows:
 ,
,  , … ,
, … ,  , and X
2 = X
n−1
, and X
2 = X
n−1
and X 2 = X n−1
and X 2 = X n−1
and X 2 = X n−1 (the property δ(X, Y) = δ(Y, X))
δ(X n , X 2) ≥ δ(X 2, X 1)
δ(X 2, X n ) ≥ δ(X 2, X 1) (the property δ(X, Y) = δ(Y, X))
 □
□
Proof of Observation 1
Let \(\bar {\rightharpoondown }\) be the relation such that \(X \bar {\rightharpoondown }_{Y} Z\) iff either \(X\rightharpoondown _{Y} Z\) or X = Z. We are first going to show that \(\bar {\rightharpoondown }\) is transitive. Let \(Y_{1}\bar {\rightharpoondown }_{X} Y_{2}\) and \(Y_{2} \bar {\rightharpoondown }_{X} Y_{3}\). Due to the definition of \(\bar {\rightharpoondown }\), we also have \(X \bar {\rightharpoondown }_{Y_{2}} X\). We can apply Lemma 4, part 2, to \(Y_{1} \bar {\rightharpoondown }_{X} Y_{2}\), \(X\bar {\rightharpoondown }_{Y_{2}} X\), and \(Y_{2} \bar {\rightharpoondown }_{X} Y_{3}\) and obtain \(Y_{1} \bar {\rightharpoondown }_{X} Y_{3}\), as desired.
Due to a standard theorem in preference logic (see for instance [16], p. 324), it follows from the transitivity of \(\bar {\rightharpoondown }_{X}\) that its strict part \(\rightharpoondown _{X}\) is also transitive. □
Proof of Observation 2
See Fig. 3. DP1: Part (a) of the figure is compatible with q ⊩ p. Let X = Cn({¬p,¬q, r}). Then (X∗p)∗q = Cn({p, q, r}) and X∗q = Cn({p, q,¬r}).
DP2: Part (b) of the figure is compatible with q ⊩ ¬p. Let X = Cn({¬p, q,¬r}). Then (X∗p)∗q = Cn({¬p, q, r}) and X∗q = X = Cn({¬p, q,¬r}).
DP3: In part (c) of the figure, let X = Cn({¬p,¬q, r}). Then (X∗p)∗q = Cn({¬p, q, r}) and X∗q = Cn({p, q, r}), hence X∗q ⊩ p but \((X \ast p) \ast q \nvdash p\).
DP4: Use the same example as in part 3, and note that \(X * q \nvdash \neg p\) but (X∗p)∗q ⊩ ¬p. □
Proof of Observation 3
DP1: Let \(\mathfrak {B}q\) be unsatisfiable within \(\mathbb {X}\) and let \(X\nvdash p\) and X∗p ⊩ p. Then X∗q = X and (X∗p)∗q = X∗p.
DP1, modified: Since q ⊩ p, the first p-containing belief set not preceding X must either be equal to or precede the first q-containing belief set not preceding X. In both cases, (X∗p)∗q = X∗q follows directly.
DP2: Part (a) of Fig. 4 is compatible with q ⊩ ¬p. Let X = Cn({¬p, q, r}). Then (X∗p)∗q = Cn({¬p, q,¬r}) but X∗q = X = Cn({¬p, q, r}).
DP3: If X = X∗q then X ⊩ p, thus X = X∗p, thus (X∗p)∗q = X∗q. If X ≠ X∗q, then X∗q ⊩ q. It follows from this and X∗q ⊩ p that X∗p is either identical to X∗q or precedes it. In both cases (X∗p)∗q = X∗q.
DP4: In part (b) of Fig. 4, let X = Cn({q}). Then (X∗p)∗q = Cn({¬p, q}) and X∗q = X = Cn({q}). It follows that \(X \ast q \nvdash \neg p\) but (X∗p)∗q ⊩ ¬p. □
Proof of Theorem 3
From (III − ) to (VI): Left logical equivalence follows from uniformity (Lemma 5), unitarity from closure, reflexivity from global regularity (since Ψ is satisfiable within \(\mathbb {X}\)), and the cumulativity of ⇒ from that of ∘.
From (VI) to (III − ): Closure follows from unitarity. For confirmation, we apply translation principle TP2. Let \(X\Vdash {\Psi }\), i.e. \(\mathfrak {B}{\scriptstyle \top }\Rightarrow {\Psi }\). We can use the cumulativity of ⇒ to show that \(\{\mathfrak {B}{\top }\}\cup {\Psi }\Rightarrow {\Xi }\) if and only if \(\mathfrak {B}{\top }\Rightarrow {\Xi }\). Due to left logical equivalence, \(\{\mathfrak {B}{\top }\}\cup {\Psi }\Rightarrow {\Xi }\) can be substituted by Ψ ⇒ Ξ. Relative success and global regularity follow from reflexivity, and the cumulativity of ∘ from that of ⇒.
Proof of Observation 4
Due to unitarity there is a belief set Y such that for all descriptors Ξ: \({\Psi }_{1}\veebar {\Psi }_{2}\Rightarrow {\Xi }\) iff \(Y\Vdash {\Xi }\). It follows from reflexivity that \(Y\Vdash {\Psi }_{1}\veebar {\Psi }_{2}\), and due to the result referred to in footnote 13, either \(Y\Vdash {\Psi }_{1}\) or \(Y\Vdash {\Psi }_{2}\). It is sufficient to prove the former case. In that case we have \({\Psi }_{1}\veebar {\Psi }_{2}\Rightarrow {\Psi }_{1}\), thus:
□
Rights and permissions
About this article
Cite this article
Hansson, S.O. Iterated Descriptor Revision and the Logic of Ramsey Test Conditionals. J Philos Logic 45, 429–450 (2016). https://doi.org/10.1007/s10992-015-9381-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-015-9381-7



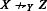 if and only if δ(X,Y)≤δ(Y,Z). Negative transmission is also closely related to an axiom introduced under the name “loop” by Lehmann et al. [
if and only if δ(X,Y)≤δ(Y,Z). Negative transmission is also closely related to an axiom introduced under the name “loop” by Lehmann et al. [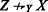
 ,
,  , …,
, …,  ,
,  and X
2 = X
n−1, then
and X
2 = X
n−1, then  .
. and X
2 = X
n−1, then
and X
2 = X
n−1, then 
