Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-07T06:47:49.559Z Has data issue: false hasContentIssue false
  • English
  • Français

COARSE REDUCIBILITY AND ALGORITHMIC RANDOMNESS

Published online by Cambridge University Press:  12 August 2016

DENIS R. HIRSCHFELDT ,
CARL G. JOCKUSCH JR. ,
RUTGER KUYPER  and
PAUL E. SCHUPP
DENIS R. HIRSCHFELDT
Affiliation:
DEPARTMENT OF MATHEMATICSUNIVERSITY OF CHICAGOCHICAGO, IL, USAE-mail: drh@math.uchicago.edu
CARL G. JOCKUSCH JR.
Affiliation:
DEPARTMENT OF MATHEMATICSUNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGNCHAMPAIGN, IL, USAE-mail: jockusch@math.uiuc.edu
RUTGER KUYPER
Affiliation:
DEPARTMENT OF MATHEMATICSUNIVERSITY OF WISCONSIN–MADISONMADISON, WI, USAE-mail: mail@rutgerkuyper.com
PAUL E. SCHUPP
Affiliation:
DEPARTMENT OF MATHEMATICSUNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGNCHAMPAIGN, IL, USAE-mail: schupp@illinois.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A coarse description of a set A ⊆ ω is a set D ⊆ ω such that the symmetric difference of A and D has asymptotic density 0. We study the extent to which noncomputable information can be effectively recovered from all coarse descriptions of a given set A, especially when A is effectively random in some sense. We show that if A is 1-random and B is computable from every coarse description D of A, then B is K-trivial, which implies that if A is in fact weakly 2-random then B is computable. Our main tool is a kind of compactness theorem for cone-avoiding descriptions, which also allows us to prove the same result for 1-genericity in place of weak 2-randomness. In the other direction, we show that if 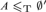$A \le _{{\rm{T}}} \emptyset {\rm{'}}$ is a 1-random set, then there is a noncomputable c.e. set computable from every coarse description of A, but that not all K-trivial sets are computable from every coarse description of some 1-random set. We study both uniform and nonuniform notions of coarse reducibility. A set Y is uniformly coarsely reducible to X if there is a Turing functional Φ such that if D is a coarse description of X, then ΦD is a coarse description of Y. A set B is nonuniformly coarsely reducible to A if every coarse description of A computes a coarse description of B. We show that a certain natural embedding of the Turing degrees into the coarse degrees (both uniform and nonuniform) is not surjective. We also show that if two sets are mutually weakly 3-random, then their coarse degrees form a minimal pair, in both the uniform and nonuniform cases, but that the same is not true of every pair of relatively 2-random sets, at least in the nonuniform coarse degrees.

Keywords

Primary 03D30Secondary 03D2803D32Coarse reducibilityalgorithmic randomnessK-triviality
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 3 , September 2016 , pp. 1028 - 1046
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Astor, E., Asymptotic density, immunity, and randomness . Computability, vol. 4 (2015), pp. 141–158.Google Scholar
Barmpalias, G., Lewis, A. E. M., and Ng, K. M., The importance of ${\rm{\Pi }}_1^0 $ classes in effective randomness , this Journal, vol. 75 (2010), pp. 387–400.Google Scholar
Bienvenu, L., Day, A. R., Greenberg, N.. Kučera, A., Miller, J. S., Nies, A., and Turetsky, D., Computing K-trivial sets by incomplete random sets . Bulletin of Symbolic Logic, vol. 20 (2014), pp. 80–90.Google Scholar
Bienvenu, L., Greenberg, N., Kučera, A., Nies, A., and Turetsky, D., Coherent randomness tests and computing the K-trivial sets . Journal of the European Mathematical Society, to appear.Google Scholar
Downey, R. G. and Hirschfeldt, D. R., Algorithmic randomness and complexity. Theory and Applications of Computability, Springer, New York, 2010.Google Scholar
Downey, R. G., Jockusch, C. G. Jr., McNicholl, T. H., and Schupp, P. E., Asymptotic density and the Ershov Hierarchy . Mathematical Logic Quarterly, vol. 16 (2015), pp. 189–195.Google Scholar
Downey, R. G., Jockusch, C. G. Jr., and Schupp, P. E., Asymptotic density and computably enumerable sets . Journal of Mathematical Logic, vol. 13 (2013) 1350005, 43 pp.Google Scholar
Downey, R. G., Nies, A., Weber, R., and Yu, L., Lowness and ${\rm{\Pi }}_2^0 $ nullsets, this Journal vol. 71 (2006), pp. 1044–1052.Google Scholar
Dzhafarov, D. D. and Igusa, G., Notions of robust information coding, to appear.Google Scholar
Figueira, S., Miller, J. S., and Nies, A., Indifferent sets , Journal of Logic and Computation, vol. 19 (2009), pp. 425–443.Google Scholar
Greenberg, N., Hirschfeldt, D. R., and Nies, A., Characterizing the strongly jump-traceable sets via randomness . Advances in Mathematics, vol. 231 (2012), pp. 2252–2293.Google Scholar
Greenberg, N. and Miller, J. S., Lowness for Kurtz randomness , this Journal, vol. 74 (2009), pp. 665–678.Google Scholar
Hirschfeldt, D. R. and Jockusch, C. G. Jr., On notions of computability theoretic reduction between ${\rm{\Pi }}_2^1 $ principles , to appear.Google Scholar
Hirschfeldt, D. R., Jockusch, C. G. Jr., McNicholl, T., and Schupp, P. E., Asymptotic density and the coarse computability bound . Computability, to appear.Google Scholar
Hirschfeldt, D. R., Nies, A., and Stephan, F., Using random sets as oracles . Journal of the London Mathematical Society, vol. 75 (2007), pp. 610–622.Google Scholar
Jockusch, C. G. Jr., Degrees of generic sets , Recursion Theory: Its Generalisations and Applications (Drake, F. R. and Wainer, S. S., editors), London Mathematical Society Lecture Note Series 45, Cambridge University Press, Cambridge, 1980, pp. 110–139.Google Scholar
Jockusch, C. G. Jr. and Schupp, P. E., Generic computability, Turing degrees, and asymptotic density . Journal of the London Mathematical Society, vol. 85 (2012), pp. 472–490.Google Scholar
Kapovich, I., Myasnikov, A., Schupp, P., and Shpilrain, V., Generic-case complexity, decision problems in group theory and random walks . Journal of Algebra, vol. 264 (2003), pp. 665–694.CrossRefGoogle Scholar
Kučera, A., An alternative priority-free solution to Post’s problem , Mathematical Foundations of Computer Science 1986 (Gruska, J., Rovan, B., and Wiederman, J., editors), Lecture Notes in Computer Science, vol. 233, Springer, Berlin, 1986, 493–500.Google Scholar
Kumabe, M. and Lewis, A. E. M., A fixed point free minimal degree . Journal of the London Mathematical Society, vol. 80 (2009), pp. 785–797.Google Scholar
Loomis, L. H. and Whitney, H., An inequality related to the isoperimetric inequality . Bulletin of the American Mathematical Society, vol. 55 (1949), pp. 961–962.Google Scholar
Maass, W., Shore, R. A., and Stob, M., Splitting properties and jump classes . Israel Journal of Mathematics, vol. 39 (1981), pp. 210–224.Google Scholar
Monin, B., Higher Computability and Randomness , Ph.D dissertation, Université Paris Diderot–Paris 7, 2014.Google Scholar
Nies, A., Computability and Randomness, Oxford University Press, Oxford, 2009.Google Scholar
Nies, A., Notes on a theorem of Hirschfeldt, Jockusch, Kuyper and Schupp regarding coarse computation and K-triviality , Logic Blog 2013, Part 5, Section 24 (Nies, A., editor), available at http://arxiv.org/abs/1403.5719.Google Scholar
Sacks, G. E., Recursive enumerability and the jump operator . Transactions of the American Mathematical Society, vol. 108 (1963), pp. 223–239.Google Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees . Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1987.Google Scholar
van Lambalgen, M., The axiomatization of randomness , this Journal, vol. 55 (1990), pp. 1143–1167.Google Scholar
Yu, L., Lowness for genericity . Archive of the Mathematical Logic, vol. 45 (2006), pp. 233–238.CrossRefGoogle Scholar