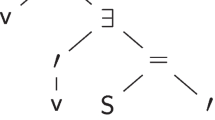Skip to main content
SpringerLink
Log in

On the Recognizing Power of the Lambek Calculus with Brackets

  • Published:
Journal of Logic, Language and Information Aims and scope Submit manuscript

Abstract

Every language recognized by the Lambek calculus with brackets is context-free. This is shown by combining an observation by Jäger with an entirely straightforward adaptation of the method Pentus used for the original Lambek calculus. The case of the variant of the calculus allowing sequents with empty antecedents is slightly more complicated, requiring a restricted use of the multiplicative unit.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. Equivalently, we may take all sequents of the form \(A {\varvec{\rightarrow }}A\) as initial sequents, as Jäger (2003) did.

  2. This is one of the two notions of recognition studied by Jäger (2003); he called this notion t-recognition.

  3. An example (adapted from Fadda and Morrill 2005) is \(\Diamond \Box ^{\downarrow }p \,\Diamond \Box ^{\downarrow }q {\varvec{\rightarrow }}\Diamond \Box ^{\downarrow }(p \bullet q)\).

  4. To be precise, Kanovich et al. (2017) were speaking of \(\mathbf {L}^{\textstyle *}\Diamond \) rather than \(\mathbf {L}\Diamond \). Jäger (2003) was dealing with \(\mathbf {L}\Diamond \) rather than \(\mathbf {L}^{\textstyle *}\Diamond \), although he did not make it entirely clear.

  5. See Kanazawa (2006) for a statement of an interpolation theorem for the implicational fragment of intuitionistic logic in terms of these links.

  6. To extend Moortgat’s (1996) proof in the presence of \(\varvec{1}\), one only need to add the reduction step

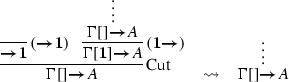
  7. Pentus’s (1999) claim of context-freeness of \(\mathbf {L}^{\textstyle *}\), as opposed to \(\mathbf {L}^{\textstyle *}_{\varvec{1}}\), is immune to this criticism since an interpolation theorem similar to Theorem 3 does hold for \(\mathbf {L}^{\textstyle *}\) and there’s no need to use \(\varvec{1}\) in converting an \(\mathbf {L}^{\textstyle *}\) grammar to a context-free grammar. The same criticism does apply to his claim about grammars based on multiplicative cyclic linear logic (CLL).

References

  • Fadda, M., & Morrill, G. (2005). The Lambek calculus with brackets. In C. Casadio, P. J. Scott, & R. A. Seely (Eds.), Language and grammar: Studies in mathematical linguistics and natural language (pp. 113–128). Stanford, CA: CSLI Publications.

    Google Scholar 

  • Jäger, G. (2003). On the generative capacity of multi-modal categorial grammars. Research on Language and Computation, 1(1), 105–125. https://doi.org/10.1023/A:1024512212054.

    Article  Google Scholar 

  • Kanazawa, M. (2006). Computing interpolants in implicational logics. Annals of Pure and Applied Logics, 142(1–3), 125–201. https://doi.org/10.1016/j.apal.2005.12.014.

    Article  Google Scholar 

  • Kanovich, M., Kuznetsov, S., Morrill, G., & Scedrov, A. (2017). A polynomial-time algorithm for the Lambek calculus with brackets of bounded order. In D. Miller (Ed.), 2nd international conference on formal structures for computation and deduction (FSCD 2017), Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany, leibniz international proceedings in informatics (LIPIcs), vol 84, (pp. 22:1–22:17). https://doi.org/10.4230/LIPIcs.FSCD.2017.22, URL http://drops.dagstuhl.de/opus/volltexte/2017/7738.

  • Kuznetsov, S. (2012). Lambek grammars with the unit. In P. de Groote, & M. J. Nederhof (Eds.), Formal grammar: 15th and 16th international conferences, FG 2010, Copenhagen, Denmark, August 2010, FG 2011, Ljubljana, Slovenia, August 2011, Revised Selected Papers (pp. 262–266). Berlin, Heidelberg: Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-32024-8_17.

    Chapter  Google Scholar 

  • Lambek, J. (1958). The mathematics of sentence structure. American Mathematical Monthly, 65, 154–170.

    Article  Google Scholar 

  • Lambek, J. (1961). On the calculus of syntactic types. In R. Jakobson (Ed.), Structure of language and its mathematical aspects (pp. 166–178). Providence, R.I.: American Mathematical Society.

    Chapter  Google Scholar 

  • Moortgat, M. (1996). Multimodal linguistic inference. Journal of Logic, Language, and Information, 5, 349–385.

    Article  Google Scholar 

  • Pentus, M. (1993). Lambek grammars are context free. In Proceedings of the eighth annual IEEE symposium on logic in computer science (pp. 429–433).

  • Pentus, M. (1997). Product-free Lambek calculus and context-free grammars. Journal of Symbolic Logic, 62, 648–660.

    Article  Google Scholar 

  • Pentus, M. (1999). Lambek calculus and formal grammars. In Provability, complexity, grammars, no. 192 in American mathematical society translations–series 2 (pp. 57–86). Providence, Rhode Island: American Mathematical Society.

  • Roorda, D. (1991). Resource logics: Proof-theoretical investigations. PhD thesis, University of Amsterdam.

  • Versmissen, J. A. G. (1996). Grammatical composition: Modes, models, modalities. PhD thesis, University of Utrecht.

Download references

Author information

Authors and Affiliations

  1. Department of Advanced Sciences, Faculty of Science and Engineering, Hosei University, 3–7–2 Kajino-cho, Koganei-shi, Tokyo, 184–8584, Japan

    Makoto Kanazawa

Authors
  1. Makoto Kanazawa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Makoto Kanazawa.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kanazawa, M. On the Recognizing Power of the Lambek Calculus with Brackets. J of Log Lang and Inf 27, 295–312 (2018). https://doi.org/10.1007/s10849-018-9269-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10849-018-9269-3

Keywords

Search

Navigation