Article contents
Computable Boolean algebras
Published online by Cambridge University Press: 12 March 2014
Extract
Feiner [F] showed that a 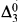 Boolean algebra need not have a computable copy (see also [T2]). Downey and Jockusch [D-J] showed that every low Boolean algebra does have a computable copy. Thurber [T3], showed that every low2 Boolean algebra has a computable copy. Here we show that every Boolean algebra which is low3, or even low4, has a computable copy.
Boolean algebra need not have a computable copy (see also [T2]). Downey and Jockusch [D-J] showed that every low Boolean algebra does have a computable copy. Thurber [T3], showed that every low2 Boolean algebra has a computable copy. Here we show that every Boolean algebra which is low3, or even low4, has a computable copy.
The results of [D-J] and [T3] were obtained by passing to linear orderings. In [D-J], there is an embedding theorem saying that any linear ordering which is 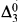 with the successor relation as an added predicate can be embedded in a slightly larger linear ordering which is computable. An isomorphism theorem of Remmel [R] is used to show that the interval algebras of the two linear orderings are isomorphic (except in a trivial case). In [T3], there is an embedding theorem saying that any linear ordering which is
with the successor relation as an added predicate can be embedded in a slightly larger linear ordering which is computable. An isomorphism theorem of Remmel [R] is used to show that the interval algebras of the two linear orderings are isomorphic (except in a trivial case). In [T3], there is an embedding theorem saying that any linear ordering which is 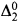 with certain added predicates can be embedded in one which is
with certain added predicates can be embedded in one which is 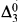 with successor. Again the isomorphism theorem of Remmel is used to show that the interval algebras are isomorphic (except in a trivial case).
with successor. Again the isomorphism theorem of Remmel is used to show that the interval algebras are isomorphic (except in a trivial case).
Here, instead of passing to linear orderings, we work directly with Boolean algebras. We begin with a review of the known results. We re-formulate the embedding theorems of Downey-Jockusch and Thurber in terms of Boolean algebras. We extract from Remmel's isomorphism theorem some information on complexity. In this way, we show that a low Boolean algebra is isomorphic to a computable one by an isomorphism which is 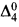 , at worst, and the same is true for a low2 Boolean algebra.
, at worst, and the same is true for a low2 Boolean algebra.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2000
References
REFERENCES
- 37
- Cited by




