Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-24T22:27:41.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential Calculus and Nilpotent Real Numbers

Published online by Cambridge University Press:  15 January 2014

Anders Kock
Anders Kock*
Affiliation:
Department of Mathematical Sciences, University of Aarhus, DK 8000 Aarhus C, Denmark, E-mail:kock@imf.au.dk
Get access Rights & Permissions [Opens in a new window]

Extract

Do there exist real numbers d with d2 = 0 (besides d = 0, of course)? The question is formulated provocatively, to stress a formalist view about existence: existence is consistency, or better, coherence.

Also, the provocation is meant to challenge the monopoly which the number system, invented by Dedekind et al., is claiming for itself as THE model of the geometric line. The Dedekind approach may be termed “arithmetization of geometry”.

We know that one may construct a number system out of synthetic geometry, as Euclid and followers did (completed in Hilbert's Grundlagen der Geometrie, [2, Chapter 3]): “geometrization of arithmetic”. (Picking two distinct points on the geometric line, geometric constructions in an ambient Euclidean plane provide structure of a commutative ring on the line, with the two chosen points as 0 and 1).

Starting from the geometric side, nilpotent elements are somewhat reasonable, although Euclid excluded them. The sophist Protagoras presented a picture of a circle and a tangent line; the apparent little line segment D which tangent and circle have in common, are, by Pythagoras' Theorem, precisely the points, whose abscissae d (measured along the tangent) have d2 = 0. Protagoras wanted to use this argument for destructive reasons: to refute the science of geometry.

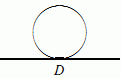
A couple of millenia later, the Danish geometer Hjelmslev revived the Protagoras picture. His aim was more positive: he wanted to describe Nature as it was. According to him (or extrapolating his position), the Real Line, the Line of Sensual Reality, had many nilpotent infinitesimals, which we can see with our naked eyes.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 9 , Issue 2 , June 2003 , pp. 225 - 230
Copyright
Copyright © Association for Symbolic Logic 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bell, J. L., A primer of infinitesimal analysis, Cambridge University Press, 1998.Google Scholar
[2] Hilbert, D., Grundlagen der Geometrie, Teubner, Leipzig, 1899, 8. ed., 1956.Google Scholar
[3] Hilbert, D. and Cohn-Vossen, S., Anschauliche Geometrie, Springer, 1932.Google Scholar
[4] Hjelmslev, J., Die natürliche Geometrie, Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg (2), (1923), pp. 1–36.Google Scholar
[5] Hjelmslev, J., Lærebog i Geometri, Jul. Gjellerups Forlag, Copenhagen, 1923.Google Scholar
[6] Hjelmslev, J., Tre Foredrag over Geometriens Grundlag, Jul. Gjellerups Forlag, Copenhagen, 1923.Google Scholar
[7] Klingenberg, W., Euklidische Ebenen mit Nachbarelementen, Mathematische Zeitschrift, vol. 61 (1954), pp. 1–25.Google Scholar
[8] Kock, A., A simple axiomatics for differentiation, Mathematica Scandinavica, vol. 40 (1977), pp. 183–193.CrossRefGoogle Scholar
[9] Kock, A., Synthetic differential geometry, Cambridge University Press, 1981.Google Scholar
[10] Kock, A., The osculating plane of a space curve — synthetic formulations, Rendiconti del Circolo Matematico di Palermo. Serie II, vol. 64 (2000), pp. 67–79.Google Scholar
[11] Lane, S. Mac, Mathematics – form and function, Springer, 1986.Google Scholar
[12] Lavendhomme, R., Basic concepts of synthetic differential geometry, Kluwer, 1996.CrossRefGoogle Scholar
[13] Lawvere, F. W., The category of categories as a foundation for mathematics, Proceedings of the conference of categorical algebra, La Jolla, 1965, Springer, 1966.Google Scholar
[14] Lawvere, F. W., Categorical dynamics, Topos theoretic methods in geometry (Kock, A., editor), No. 30, Aarhus Math. Inst. Var. Publ., 1979.Google Scholar
[15] Lawvere, F. W., Towards a description in a smooth topos of the dynamically possible motions and deformations of a continuous body, Cahiers de Topologie et Géométrie Différentielle Catégoriques, vol. 21 (1981), pp. 277–392.Google Scholar
[16] Lawvere, F. W., Outline of synthetic differential geometry, 02 1998, available at http://www.acsu.buffalo.edu/~wlawvere/SDG Outline.pdf.Google Scholar
[17] Moerdijk, I. and Reyes, G. E., Smooth infinitesimal analysis, Springer, 1991.Google Scholar
[18] Weil, A., Théorie des points proches sur les variétes différentiables, Colloq Top. et Géom. Diff. Strasbourg, 1953.Google Scholar
[19] Weyl, H., Philosophy of mathematics and natural science, Princeton University Press, 1949.Google Scholar