Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-31T21:09:06.569Z Has data issue: false hasContentIssue false
  • English
  • Français

Combinatorial properties of filters and open covers for sets of real numbers

Published online by Cambridge University Press:  12 March 2014

Claude Laflamme  and
Marion Scheepers
Claude Laflamme
Affiliation:
Department of Mathematics, The University of Calgary, Calgary, Alberta, Canada T2N-1N4 E-mail: laf@math.ucalgary.ca
Marion Scheepers
Affiliation:
Department of Mathematics, Boise State University, Boise, Idaho 83725, USA E-mail: mscheep@micron.net
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyze combinatorial properties of open covers of sets of real numbers by using filters on the natural numbers. In fact, the goal of this paper is to characterize known properties related to ω-covers of the space in terms of combinatorial properties of filters associated with these ω-covers. As an example, we show that all finite powers of a set 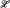of real numbers have the covering property of Menger if, and only if, each filter on ω associated with its countable ω-cover is a P+ filter.

Keywords

Filteromega covermeagermeasure zerocovering propertyinfinite gamecardinal number
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 3 , September 1999 , pp. 1243 - 1260
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bartoszyński, T., On the structure of measurable filters on a countable set, Real Analysis Exchange, vol. 17 (1992), pp. 681–701.CrossRefGoogle Scholar
[2] Canjar, R. M., On the generic existence of special ultrafilters, Proceedings of the American Mathematical Society , vol. ? (19??), pp. ???–???Google Scholar
[3] Galvin, F. and Miller, A. W., γ-sets and other singular sets of real numbers, Topology and its Applications, vol. 17 (1984), pp. 145–155.CrossRefGoogle Scholar
[4] Garcia-Ferreira, S. and Laflamme, C., The γP property and the reals, preprint.Google Scholar
[5] Gerlits, J. and Nagy, Zs., Some properties of C(X), I, Topology and its Applications, vol. 14 (1982), pp. 151–161.CrossRefGoogle Scholar
[6] Hurewicz, W., Über die Verallgemeinerung des Borelschen Theorems, Mathematische Zeitschrift, vol. 24 (1925), pp. 401–421.CrossRefGoogle Scholar
[7] Hurewicz, W., Über Folgen stetiger Funktionen, Fundamenta Mathematicae, vol. 9 (1927), pp. 193–204.CrossRefGoogle Scholar
[8] Just, W., Miller, A. W., Scheepers, M., and Szeptycki, P. J., The combinatorics of open covers (II), Topology and its Applications, vol. 73 (1996), pp. 241–266.CrossRefGoogle Scholar
[9] Laflamme, C., Strong meager properties for filters, Fundamenta Mathematicae, vol. 146 (1995), pp. 283–293.CrossRefGoogle Scholar
[10] Nowik, A., Scheepers, M., and Weiss, T., The algebraic sum of sets of real numbers with strong measure zero sets, this Journal, to appear.Google Scholar
[11] Rothberger, F., Eine Verscharfung der Eigenschaft c, Fundamenta Mathematicae, vol. 30 (1938), pp. 50–55.CrossRefGoogle Scholar
[12] Sakai, M., Property C″ and function spaces, Proceedings of the American Mathematical Society, vol. 104 (1988), pp. 917–919.Google Scholar
[13] Scheepers, M., Combinatorics of open covers III. games, C P ( ), Fundamenta Mathematicae, to appear.Google Scholar
[14] Scheepers, M., Combinatorics of open covers I: Ramsey theory, Topology audits Applications, vol. 69 (1996), pp. 31–62.CrossRefGoogle Scholar
[15] Talagrand, M., Filtres: mesurabilité, rapidité, propriété de Baire forte, Studia Mathematica, vol. 67 (1980), pp. 13–43.CrossRefGoogle Scholar