Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-06T02:41:19.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Theories with recursive models

Published online by Cambridge University Press:  12 March 2014

Manuel Lerman  and
James H. Schmerl
Manuel Lerman
Affiliation:
University of Connecticut, Storrs, Connecticut 06268
James H. Schmerl
Affiliation:
University of Connecticut, Storrs, Connecticut 06268
Get access Rights & Permissions [Opens in a new window]

Extract

A structure 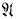is recursive if the set of quantifier-free sentences in the complete diagram ⊿(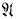) of 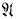is recursive. It has been known for some time that every decidable theory has a recursive model. In fact, every decidable theory has a decidable model 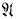(that is a model 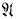such that ⊿(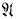) is recursive). In this paper we find other conditions which imply that a theory have a recursive model.

In §1 we study the relation between an ℵ0-categorical theory T having a recursive model and the complexity of the quantificational hierarchy of that theory. We let ∃0 denote the set of quantifier-free sentences, and let ∃n÷1 denote the set of sentences beginning with an existential quantifier and having n alternations of quantifiers. (∀n is defined analogously.) Then we show that if T is an arithmetical ℵ0-categorical theory such that T ⋂ ∃n÷2 is Σn÷10 for each n < ω, then T has a recursive model. We show that this is a best possible result by giving an example of a ⊿n÷20 ℵ0-categorical theory T such that T ⋂ ∃n÷1 is recursive yet T has no recursive model.

In §2 we consider the theory of trees. Ershov [1] had proved that every Σ10 theory of trees has a recursive model. We show this to be best possible by giving an example of a ⊿20 theory of trees which has no recursive model.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 1 , March 1979 , pp. 59 - 76
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ershov, J., Skolem functions and constructive models, Algebra i Logika, vol. 12(1973), pp. 644–654.Google Scholar
[2]Goncharov, S. S., and Nurtazin, A. T., Constructive models of complete solvable theories, Algebra i Logika, vol. 12(1973), pp. 125–142.Google Scholar
[3]Harrington, L., Recursively presentable prime models, this Journal, vol. 39(1974), pp. 305–309.Google Scholar
[4]Henson, C. W., Countable homogeneous relational structures and ℵ0-categorical theories, this Journal, vol. 37(1972), pp. 494–500.Google Scholar
[5]Läuchli, H. and Leonard, J., On the elementary theory of linear order, Fundamenta Mathematicae, vol. 59(1966), pp. 109–116.CrossRefGoogle Scholar
[6]Millar, T. S., Foundations of recursive model theory, Annals of Mathematical Logic, vol. 13(1978), pp. 45–72.CrossRefGoogle Scholar
[7]Morley, M.D., Decidable models, Israel Journal of Mathematics, vol. 25(1976), pp. 233–240.CrossRefGoogle Scholar
[8]Nash-Williams, C. S. J., On well-quasi-ordering finite trees, Proceedings of the Cambridge Philosophical Society, vol. 59(1963), pp. 833–835.CrossRefGoogle Scholar
[9]Peretyat'kin, M. G., Every recursively enumerable extension of a theory of linear order has a constructible model, Algebra i Logika, vol. 12(1973), pp. 211–219.Google Scholar
[10]Peretyat'kin, M. G., On complete theories with a finite number of denumerable models, Algebra i Logika vol. 12(1973), pp. 550–576.Google Scholar