Abstract
G. Schiemer has recently ascribed to Carnap the so-called domains-as-fields conception of models, which he subsequently used to defend Carnap’s treatment of extremal axioms against J. Hintikka’s criticism that the number of tuples in a relation, and not the domain of discourse, is optimised in Carnap’s treatment. We will argue by a careful textual analysis, however, that this domains-as-fields conception cannot be applied to Carnap’s early semantics, because it includes a notion of submodel and subrelation that is not only absent from Carnap’s work at that time, but even contradicts it. As a consequence, Schiemer’s defense of Carnap’s extremal axioms against Hintikka’s criticism fails. We will reconcile Carnap’s treatment of extremal axioms and Hintikka’s observation by taking into account the practice of axiomatics in the early twentieth century. If one realises that, in Carnap’s time, a predicate for the domain of discourse was often introduced in the formal theory, and that Carnap defined such predicates from the basic relations of an axiom system, the apparent disagreement between optimising relations and optimising domains disappears.
Similar content being viewed by others
Notes
Henceforth we will refer to the second part of Untersuchungen as Untersuchungen II.
Under domain of discourse we understand the pre-theoretical notion of “things” that a (formal) theory is about. This notion can be encoded in a formal theory as, for example, the range of quantification or by a predicate in the language. (See Betti and Loeb 2012, p. 246.)
Der Begriff “Individuum” ist ein relativer Begriff: derselbe Gegenstand, der in einem gewissen Zusammenhange Individuum ist, kann in einem erweiterten Zusammenhange Relation sein, indem hier die Glieder auftreten, während von solchen in dem ersten Zusammenhang nicht die Rede ist.
All translations are the author’s unless otherwise specified.
Die in einem Axiomensystem auftretenden Zeichen (z.B. Wörter) für die Grundbegriffe des Axiomensystems nennen wir die “Grundzeichen”. Sie haben nach der genannten Auffassung keine feste Bedeutung, sondern können je nach dem Anwendungsfall auf verschiedene Gegenstände bezogen werden. Die Grundzeichen sind demnach Variable, und die einzelnen Axiome, sowie auch das ganze Axiomensystem sind Aussagefunktionen, nicht Aussagen (…).
In his early logical work Carnap doesn’t make an essential distinction between concepts and objects. He writes:
We can (…) almost say that the concept and its object are the same. This identity doesn’t mean, however, a substantiation of the concept, but rather conversely a “functionalisation” of the object. (Carnap 1928, p. 6)
(The above cited passage may be understood as a general allusion to Cassirer (1910). See Mormann (2006, p. 31). We can find this same equation of concepts and objects in Untersuchungen II.
We will not go into Carnap’s notion of true proposition here.
Schreiben wir für f(R, S, T) kurz \(f\mathcal{R},\) und sind R 1, S 1, T 1 bestimmte, etwa arithmetische Relationen, die zulässige Werte der Variabeln R, S, T sind, so können wir auch für das geordnete Relationssystem R 1, S 1, T 1 eine abkürzende Bezeichnung einführen, etwa \(\mathcal{R}_1.\) Das Modell \(\mathcal{R}_1\) ist dann ein Wert der Modellvariablen \(\mathcal{R}.\)
Beispiel 2.7.1 A 1 bezeichne die zweistellige Relation, deren Gliederpaare die Zahlenpaare 3, 5 und 6, 7 und 8, 9 sind; also (nach §1.5): A 1 = Df [3′5, 6′7, 8′9]. Ferner sei A 2 = Df [3′7, 9′2]; A 3 = Df [2′5]; A 4 = Df [3′4, 4′6, 8′9]. Die einstellige Relation (oder Klasse), deren Glieder diese vier Relationen sind, sei K; also K = Df [A 1, A 2, A 3, A 4]. Die Variabele P einer bestimmtem Aussagefunktion fP habe nun den Typus t(0) (oder t1), also die Stufe 1, was wir durch die Schreibung P (0) zum Ausdruck bringen können. Das besagt, daß die P-Werte einstellige Relationen (Klassen) von Individuen sind. Da K eine einstellige Relation von zweistellige Relationen zwischen Zahlen ist, so können wir K als Wert der Variablen P nehmen, indem wir die zweistellige Relationen zwischen Zahlen als Individuen ansehen.
gQ ((00)) sei eine andere Aussagefunktion. Nach der Typusbezeichnung ist Q von zweiter Stufe und die Q-Werte sind einstellige Relationen von zweistelligen Relationen zwischen Individuen. Hier können wir, obwohl die Relationsvariabele Q einen anderen Typus hat als P, doch wieder dieselbe Relation K als Wert von Q nehmen; wir müssen aber dann andere Gegenstände zu Individuen nehmen, nämlich jetzt die Zahlen selbst.
We can find a similar statement in Carnap (1934a, p. 271).
For more on analyticity, see e.g Coffa (1991, pp. 286–293) and Schiemer and Reck (forthcoming, p. 17).
For more on Carnap’s notions of axiom system and model, see Carnap (1937), §71e.
For more on extremal axioms by Carnap, see also Awodey and Reck (2003) §4.2.
Schiemer uses the term “partial relation” to translate “Teilrelation”.
The notion of submodel is even stricter in Schiemer (2012). There only restriction of the field is taken into account:
Carnap’s formal models of an axiomatic theory can thus be reconstructed (in modern notation) as tuples of the form \({\mathfrak{M}} = (D, \{R_{i}\}_{i \in I})\) where {R i } i∈I is a family of relations and \(D = \bigcup\nolimits_{i\in I} Fld(R_i)\) is the respective model domain. Accordingly, a submodel \({\mathfrak{N}} = (D, \{R_i\}_{i\in I})\) of \({\mathfrak{M}}\) is conceived as a family of restrictions R i ′ of the relations R i to \(D'\subseteq D\) (…) (Schiemer (2012), p. 622).
Subsumtion (“R sub S”); jedes R-Paar ist auch ein S-Paar; R “ist enthalten in” S, R ist “Teilrelation” von S:
We will come back below to the definition of restriction, which Schiemer (2013) mistakes for that of subrelation.
Die einstelligen Relationen heißen auch “Klassen”; wir fassen hier also die Klassen (nach dem Vorgange von Weyl) mit unter den Terminus “Relationen”, was die Begriffsbildung und die Formulierung der Theorie sehr vereinfacht. (Carnap 2000, p. 65).
Ist jedes n-tupel von P auch ein solches von Q, so heißt P eine “Teilrelation” von Q; in Zeichen: Trl(P, Q); die Definition lautet (die genaue Form kann nicht allgemein, sondern nur für bestimmte Stellenzahlen gegeben werden):
Die Teilrelation von R, die durch Beschränkung des Vorbereiches von R auf die Klasse α entsteht, wird bezeichnet mit \(\alpha\;\upharpoonleft\; R\) (gelesen “R vorbeschränkt auf α”); entsprechend bei Beschränkung des Nachbereiches: \(R\;\upharpoonright\;\beta\) (“R nachbeschränkt auf β”); im Falle beider Beschränkungen: \(\alpha\;\upharpoonleft\; R\;\upharpoonright \;\beta;\) bei Beschränkung des Feldes: R
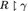 γ (“R beschränkt auf γ”).
γ (“R beschränkt auf γ”).Bezeichnen wir die Grundrelation des AS mit R und das Produkt der ursprünglichen Axiome mit fR, so lautet (…):
-
(a)
Beschränktheitsaxiom: \((P): \,P\,\subset\!\!\!\!\cdot\,\,R.fP.\supset.P=R\)
-
(b)
Vollständigkeitsaxiom: \((Q):\, R\, \subset\!\!\!\!\cdot\,\, Q.fQ.\supset.R=Q\)
In Worten:
-
(a)
Beschränktheitsaxiom: “Jedes [sic] Teilrelation von R, die die anderen Axiomen [sic] erfüllt, fällt mit R zusammen”.
-
(b)
Vollständigkeitsaxiom: “Jedes [sic] Relation, deren Teilrelation R ist und die die anderen Axiomen [sic] erfüllt, fällt mit R zusammen”.
(RC 081-01-04)
-
(a)
Intransitivity should here be understood in the strong sense: for all a, b, c, if R(a, b) and R(b, c), then it is not the case that R(a, c).
\(\hbox{Tm}({\mathfrak{P}},{\mathfrak{P}}^{\prime})\): echtes Teilmodell. Tr(P, Q) echte Teilrelation
$$ \begin{array}{lll} \hbox{Falls} & \left. \begin{array}{l} P: P,Q,R\\ P': P', Q', R' \end{array}\right\} & \hbox{Tm}(P,P') \hbox{ bedeutet dann:} \\ & & ((\hbox{Tr }(P,P') \lor P=P')\& (Q\ldots)\& (R\ldots)\\ & & \& (\hbox{Tr }(P,P')\lor\hbox{ Tr }(Q,Q')\lor\hbox{ Tr}(R,R')) \end{array} $$Note the remarks on analyticity in Sect. 2. A corresponding notion of substructure formulated without the notion of analyticity can be found in Untersuchungen II:
$$ \hbox{Ts}_f =_{df} \hat{{\mathfrak{R}}}\hat{{\mathfrak{S}}}((\exists R,S).(R\,\subset\!\!\!\!\cdot\,\,S.fR.fS.R\varepsilon{\mathfrak{R}}.S \varepsilon{\mathfrak{S}}.{\mathfrak{R}} \neq{\mathfrak{S}}[.]{\mathfrak{R}},{\mathfrak{S}}\varepsilon\text{nr}) $$(RC 081-01-05)
We find corresponding definitions of the extremal axioms for structures also in Untersuchungen II: RC 081-01-10.
Also Schiemer makes the connection between Carnap’s practice and Tarski’s use of a domain predicate, but does not mention definability: see Schiemer (2013, p. 509). For more on the use of domain predicates see Schiemer and Reck (forthcoming, p. 34/35).
Grundbegriff: EL. (\(\ldots\))
-
x EL y heißt: die Menge x ist Element der Menge y.
-
Abgeleitete Begriffe. Die Mengen: me = Df C`EL (diese “Mengen” sind nicht Klassen, sondern Individuen!).
-
Drei Grundbegriffe: Null, Zahl, Nachfolger; wir bezeichnen sie mit nu, za, Nf.
Grundbegriff: Vorgänger Vg. (\(\ldots\))
Wir definieren jetzt: D 1′. za = Df C`Vg.
Einziger Grundbegriff: ger, die Klasse der Geraden, jede Gerade genommen als Klasse ihrer Punkte (\(\ldots\))
Die Punkte: D 1. \({\bf pu} =_{Df} {\sf s}\hbox{`}{\bf ger}\) (bei Pieri zweiter Grundbegriff).
An additional observation in favor of our interpretation may be that Carnap’s study on extremal axioms seems to presuppose an absolute existence axiom (RC 081-01-04), which Bonk and Mosterin rephrase as “∃x Fx” Carnap 2000, p. 50). This would mean that there exists a basic predicate (F) in the language that singles out the domain of discourse, and that there is thus a direct relation between optimising the model (of this relation) and optimising the domain of discourse.
References
Awodey, S., & Reck, E. H. (2003). Completeness and categoricity. Part I: Nineteenth-century axiomatics to twentieth-century metalogic. History and Philosophy of Logic, 23, 1–30.
Betti, A., & Loeb, I. (2012). On Tarski’s foundations of the geometry of solids. Bulletin of Symbolic Logic, 18(2), 230–260.
Carnap, R. (1928). Der logische Aufbau der Welt (2nd edn.). Hamburg 1961.
Carnap, R. (1929). Abriss der Logistik. Wien.
Carnap, R. (1934a). Die Antinomien und die Unvollständigkeit der Mathematik. Monatshefte für Mathematik, 41(1), 263–284.
Carnap, R. (1934b). Logische Syntax der Sprache. Wien, translated into English as Carnap (1937).
Carnap, R. (1937). The logical syntax of language. London: Kegan Paul, Trench, Trubner.
Carnap, R. (2000). Untersuchungen zur allgemeinen Axiomatik. Wissenschaftliche Buchgesellschaft Darmstadt.
Carnap, R., & Bachmann, F. (1936). Über Extremalaxiome. Erkenntnis, 166–188, translated as Carnap and Bachmann (1981).
Carnap, R., & Bachmann, F. (1981). On extremal axioms. History and Philosophy of Logic, 2, 67–85, translation of Carnap and Bachmann (1936) by H.G. Bohnert.
Cassirer, E. (1910). Substanzbegriff und Funktionsbegriff: Untersuchungen über die Grundfragen der Erkenntniskritik. Berlin: Cassirer.
Coffa, J. (1991). The semantic tradition from Kant to Carnap: To the Vienna Station. Cambridge: Cambridge University Press.
Friedman, M. (1988). Logical truth and analyticity in Carnap. In W. Aspray, & P. Kitcher (Eds.), History and philosophy of modern mathematics (pp. 82–94). Minneapolis: University of Minnesota Press
Givant, S. R., & Mackenzie, R. (Eds.). (1986). Alfred Tarski: Collected Papers (Vol. 1). Birkhäuser.
Gödel, K. (1931). Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Mh. Math. Phys., xxxviii, 173–198
Gómez-Torrente, M. (1996) Tarski on logical concequence. Notre Dame Journal of Formal Logic, 37(1), 125–151
Hilbert, D. (1903). Grundlagen der Geometrie. B.G. Teubner (2nd edn.) (first edition: 1889).
Hintikka, J. (1991). Carnap, the universality of language and extremality axioms. Erkenntnis, 35(1–3), 325–336.
Mancosu, P. (2006) Tarski on models and logical consequence. In J. Ferreirós, & J. J. Gray (Eds.), The architecture of modern mathematics (pp. 209–237). Oxford: Oxford University Press
Mancosu, P. (2010). Fixed- versus variable-domain interpretations of Tarski’s account of logical consequence. Philosophy Compass, 5(9), 745–759.
Mormann T. (2006). Between Heidelberg and Marburg: The Aufbau’s Neo-Kantian Origins and the AP/CP-Divide. Sapere Aude!, 1, 22–50
Rédei, M. (Ed.). (2005). John von Neumann: Selected letters. Providence, RI: American Mathematical Society
Schiemer, G. (2012). Carnap on extremal axioms, “completeness of the models,” and categoricity. The Review of Symbolic Logic, 5(4), 613–641.
Schiemer, G. (2013). Carnap’s early semantics. Erkenntnis, 78(1), 487–522.
Schiemer, G., & Reck, E. H. (forthcoming) Logic in the 1930s: Type theory and model theory. The Bulletin of Symbolic Logic.
Tarski, A. (1929). Les fondaments de la géométrie des corps. Annales de la Société Polonaise de Mathématiques, 29–34, reprinted in Givant and Mackenzie (1986).
Tarski, A. (1933). Pojęcie prawdy w językach nauk dedukcyjnych. Nakładem / Prace Towarzystwa Naukowego Warszawskiego, wydzial III, 34.
Tarski, A. (1935). Der Wahrheitsbegriff in den formalisierten Sprachen. Studia Philosophica, 1, 261–405.
Whitehead, A., & Russell, B. (1910, 1912, 1913, 1925). Principia Mathematica. Cambridge: Cambridge University Press.
Acknowledgments
The author thanks Georg Schiemer, for sending her his recent papers, for discussions, and for his comments on an earlier version of this paper. She thanks Stefan Roski for many interesting discussions on Carnap and Carnap’s notion of model. She also thanks Arianna Betti, Hein van den Berg, Rik Peels, Jeroen de Ridder, Stefan Roski, Jeroen Smid, and René van Woudenberg for comments on an earlier version of this paper. Finally she thanks both referees for their insightful remarks. Work on this paper was made possible by ERC Starting Grant TRANH 203194. All passages from the Rudolf Carnap Papers are quoted by permission of the University of Pittsburgh. All rights reserved.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Loeb, I. Submodels in Carnap’s Early Axiomatics Revisited. Erkenn 79, 405–429 (2014). https://doi.org/10.1007/s10670-013-9501-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10670-013-9501-0




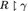 γ (“R beschränkt auf γ”).
γ (“R beschränkt auf γ”).