Abstract
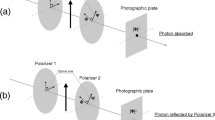
We formulate an elementary statistical game which captures the essence of some fundamental quantum experiments such as photon polarization and spin measurement. We explore and compare the significance of the principle of maximum Shannon entropy and the principle of minimum Fisher information in solving such a game. The solution based on the principle of minimum Fisher information coincides with the solution based on an invariance principle, and provides an informational explanation of Malus' law for photon polarization. There is no solution based on the principle of maximum Shannon entropy. The result demonstrates the merits of Fisher information, and the demerits of Shannon entropy, in treating some fundamental quantum problems. It also provides a quantitative example in support of a general philosophy: Nature intends to hide Fisher information, while obeying some simple rules.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
W. Yourgrau and S. Mandelstam, Variational Principles in Dynamics and Quantum Theory, 2nd edn. (Pitman, London, 1960).
J. von Neumann, Mathematical Foundations of Quantum Mechanics (Princeton University Press, New Jersey, 1955).
E. T. Jaynes, “Information theory and statistical mechanics, I & II,” Phys. Rev. 106, 620–630 (1957); 108, 171-190 (1957).
C. Brukner and A. Zeilinger, “Conceptual inadequacy of the Shannon information in quantum measurements,” Phys. Rev. A 63, 022113, 1–10 (2001).
B. R. Frieden and B. H. Soffer, “Lagrangians of physics and the game of Fisher-information transfer,” Phys. Rev. E 52, 2274–2286 (1995).
B. R. Frieden, Physics from Fisher Information: A Unification (Cambridge University Press, 1998).
R. A. Fisher, “Theory of statistical estimation,” Proc. Camb. Phil. Soc. 22, 700–725 (1925).
J. H. Wheeler, “Information, physics, quantum: the search of links,” in Complexity, Entropy, and Physics of Information, Z. H. Zurek, ed. (Addison-Wesley, Reading, MA, 1990), pp. 3–28.
J. Summhammer, “Maximum predictive power and the superposition principle,” Int. J. Theor. Phys. 33, 171–178 (1994).
J. Summhammer, “Structure of probabilistic information and quantum laws,” arXiv: quant-ph/0102099, contribution to conference Foundations of Probability and Physics, Vaxjo University, Sweden, 27 Nov.-1 Dec. 2000.
A. Zeilinger, “A foundational principle for quantum mechanics,” Found. Phys. 29, 631–643 (1999).
C. Brukner and A. Zeilinger, “Malus' law and quantum information,” Acta Physica Slovaca, 49, 647–652 (1999).
N. Wiener, Cybernetics (MIT Press, Cambridge, MA, 1948).
C. E. Shannon and W. Weaver, The Mathematical Theory of Communication (University of Illinois Press, Urbana, 1949).
L. Brillouin, Science and Information (Academic, New York, 1956).
L. Szilard, “Ñber die Entropieverminderung in einem thermodynamischen System bei eingriffen intelligenter wesen,” Z. Phys. 53, 840–856 (1929) (an English translation appeared in Behavioral Sci. 9, 301-310 1964)).
J. Hilgevoord and J. B. M. Uffink, “The mathematical expression of the uncertainty principle,” in Microphysical Reality and Quantum Formalism, A. van der Merwe et al., eds. (Kluwer Academic, Dordrecht, 1988), pp. 91–114.
S. L. Luo, “Fisher information matrix of Husimi distribution,” J. Stat. Phys. 102, 1417–1428 (2001).
H. Cramér, Mathematical Methods of Statistics (Princeton University Press, Princeton, 1946).
T. M. Cover and J. A. Thomas, Elements of Information Theory (Wiley, New York, 1991).
P. A. M. Dirac, The Principles of Quantum Mechanics, 4th edn. (Clarendon, Oxford, 1958).
R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Vol. III (Addison-Wesley, Reading, MA, 1965).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Luo, S. Maximum Shannon Entropy, Minimum Fisher Information, and an Elementary Game. Foundations of Physics 32, 1757–1772 (2002). https://doi.org/10.1023/A:1021454807474
Issue Date:
DOI: https://doi.org/10.1023/A:1021454807474