Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-19T00:57:05.470Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on computable real fields

Published online by Cambridge University Press:  12 March 2014

E. W. Madison
E. W. Madison*
Affiliation:
University of Iowa
Get access Rights & Permissions [Opens in a new window]

Extract

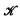It is well known that every field (formally, real field 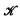) has an algebraic closure 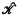(real-closure 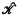). This is to say 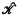is an algebraic extension of 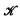which is algebraically closed (real-closed). Of course, certain properties of 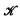carry over to 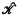. In particular, M. O. Rabin has proved in [3] that the algebraic closure—which is of course unique up to isomorphism—of a computable field is computable. The purpose of this note is to establish an analogue of Rabin's theorem for formally real fields. It is clear that a direct analogue can be formulated only in the case of ordered fields, for otherwise there may be many (nonisomorphic) such .

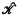Type
Research Article
Information
The Journal of Symbolic Logic , Volume 35 , Issue 2 , June 1970 , pp. 239 - 241
Copyright
Copyright © Association for Symbolic Logic 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Erdös, P., Gillman, L. and Henriksen, M., An isomorphism theorem for real-closed fields, Annals of mathematics (2), vol. 61 (1955).CrossRefGoogle Scholar
[2]Lachlan, A. H. and Madison, E. W., Computable fields and arithmetically definably ordered fields, Proceedings of the American Mathematical Society (to appear).Google Scholar
[3]Rabin, M. O., Computable algebra, Transactions of the American Mathematical Society, vol. 95 (1960), pp. 341–360.Google Scholar
[4]van der Waerden, B. L., Modern Algebra, Vol. I, Ungar, New York, 1949 and 1950.Google Scholar