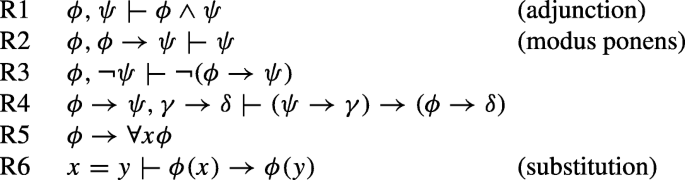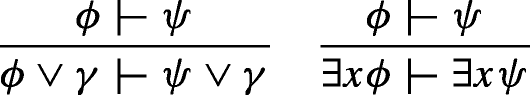Abstract
I show that it is not possible to uniquely characterize classical logic when working within classical set theory. By building on recent work by Eduardo Barrio, Federico Pailos, and Damian Szmuc, I show that for every inferential level (finite and transfinite), either classical logic is not unique at that level or there exist intuitively valid inferences of that level that are not definable in modern classical set theory. The classical logician is thereby faced with a three-horned dilemma: Give up uniqueness but preserve characterizability, give up characterizability and preserve uniqueness, or (potentially) preserve both but give up modern classical set theory. After proving the main result, I briefly explore this third option by developing an account of classical logic within a paraconsistent set theory. This account of classical logic ensures unique characterizability in some sense, but the non-classical set theory also produces highly non-classical meta-results about classical logic.
Similar content being viewed by others
References
Barrio, E., Pailos, F., & Szmuc, D. (2019). (Meta)Inferential Levels of Entailment beyond the Tarskian Paradigm. Synthese https://doi.org/10.1007/s11229-019-02411-6.
Cook, R. (2007). Embracing revenge: on the indefinite extensibility of language. In J.C. Beall (Ed.) Revenge of the Liar: New Essays on the Paradox.
Barrio, E., & Pailos, F. (2020). A Hierarchy of Classical and Paraconsistent Logics. Journal of Philosophical Logic, 49(1), 93–120.
Brady, R., & Routley, R (1989). The Non-Triviality of Extensional Dialectical Set Theory. In G. Priest, R. Routley, & J. Norman (Eds.) Paraconsistent Logic: Essays on the Inconsistent (pp. 415–436). Munich: Philosophia Verlag.
Brady, R. (2006). Universal Logic. Stanford: California: CSLI.
Carnielli, W., & Coniglio, M.E. (2016). Paraconsistent set theory by predicating on consistency. Journal of Logic Computation, 26, 97–116.
Cobreros, P., La Rosa, E., & Tranchini, L. (2020). (I Can’t Get No) Antisatisfaction. Synthese. https://doi.org/10.1007/s11229-020-02570-x.
Dicher, B., & Paoli, F. (2019). ST, LP, and Tolerant Metainferences. In C. Başkent T. Ferguson (Eds.) Graham Priest on Dialetheism and Paraconistency. Switzerland: Springer.
Mendelson, E. (2001). Introduction to Mathematical Logic. London: Chapman & Hall/CRC.
Priest, G. (1995). Beyond the Limits of Thought. Cambridge: Cambridge Unviersity Press.
Priest, G. (2006). In contradiction: a study of the transconsistent Expanded ed. Oxford: Clarendon Press.
Priest, G. (2013). Indefinite Extensibility—Dialetheic Style. Studia Logica., 101, 1263–1275.
Routley, R. (1977). Ultralogic as Universal. Relevance Logic Newsletter, 2, 50–90 and 138-175. Reprinted in Routley, R. and Weber, Z. (2019) Ultralogic as Universal. Springer, 1–121.
Russell, B. (1905). On some difficulties in the theory of transfinite numbers and order types. Proceedings of the London Mathematical Society, 4, 29–53.
Scambler, C. (2020). Classical Logic and the Strict Tolerant Hierarchy. Journal of Philosophical Logic, 49, 351–370.
Scambler, C. (2020). Transfinite Meta-inferences. Journal of Philosophical Logic. https://doi.org/10.1007/s10992-020-09548-7.
Absolute Generality.
Tourville, N., & Cook, R.T. (2016). Embracing the technicalities: expressive completeness and revenge. The Review of Symbolic Logic, 9(2), 325–58.
Weber, Z. (2010). Transfinite numbers in paraconsistent set theory. The Review of Symbolic Logic, 3(1), 71–92.
Weber, Z. (2012). Transfinite cardinals in paraconsistent set theory. The Review of Symbolic Logic, 5, 269–293.
Weber, Z., Badia, G., & Girard, P. (2016). What Is an Inconsistent Truth Table?. Australasian journal of Philosophy, 94, 533–548.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: The Logic and Set Theory of Section 4
Appendix: The Logic and Set Theory of Section 4
The following are logical and set-theoretic axioms, rules, and definitions from [20] (with the addition of an induction axiom) that constitute the background set theory in Section 4 above. I also list the various key facts that are used in proofs of results in Section 4.
Two technical comments about this set theory are in order. First, the logic from [20] differs slightly from that of [19]. In [19], what I list as R3 and R4 below are presented in axiom form, which means that the logic of [20] is slightly weaker. The benefit of choosing the weaker logic is that it is covered by Brady’s non-triviality proof from [4]. However, as Weber points out in a footnote on [20, p. 271], everything from [19] can still be obtained with this weaker logic. Second, I add to the logic of [20] an induction axiom, stating that induction holds of any recursively defined set. While weak forms of transfinite recursion and induction are provable in [19, p. 88], they are just that: weak. To ensure that the recursive definitions of Section 4 are adequately strong, I follow the precedent of Brady [5, ch. 9] and Weber et al. [21] by simply adding an induction axiom to the theory.
-
Logical axioms:
$$ \begin{array}{@{}rcl@{}} \begin{array}{llll} \mathrm{A}1 & \quad \phi \to \phi \\ \mathrm{A}2 & \quad (\phi \wedge \psi) \to \phi \\ \mathrm{A}3 & \quad (\phi \wedge \psi) \to \psi \\ \mathrm{A}4 & \quad (\phi \wedge (\psi \vee \gamma)) \to ((\phi \wedge \psi) \vee (\phi \vee \gamma)) & \text{(distribution)} \\ \mathrm{A}5 & \quad ((\phi \to \psi) \wedge (\psi \to \gamma)) \to (\phi \to \gamma) & \text{(conjunctive syllogism)}\\ \mathrm{A}6 & \quad ((\phi \to \psi) \wedge (\phi \to \gamma)) \to (\phi \to (\psi \wedge \gamma))\\ \mathrm{A}7 & \quad (\phi \to \neg \psi) \to (\psi \to \neg \phi) & \text{(contraposition)}\\ \mathrm{A}8 & \quad \neg \neg \phi \to \phi & \text{(double negation elimination)}\\ \mathrm{A}9 & \quad \phi \vee \neg \phi & \text{(excluded middle)} \\ \mathrm{A}10 & \quad \forall x \phi \to \phi(y/x) & \text{where } y \text{ is free for } x \text{ in } \phi\\ \mathrm{A}11 & \quad \forall x (\phi \to \psi) \to (\phi \to \forall x \psi) & \text{where } x \text{ is not free in } \phi \\ \mathrm{A}12 & \quad \forall x (\phi \vee \psi) \to (\phi \vee \forall x \psi) & \text{where } x \text{ is not free in } \phi \end{array} \end{array} $$ -
Logical rules:
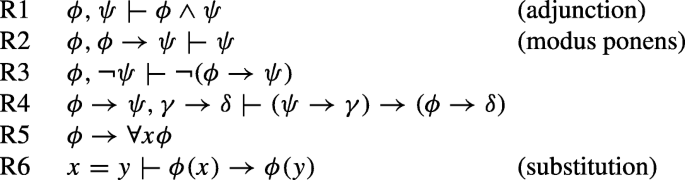
It is worth noting that the more familiar form of contraposition (ϕ → ψ) → (¬ψ →¬ϕ) can also be derived. [19, p. 74]
-
Structural rules:
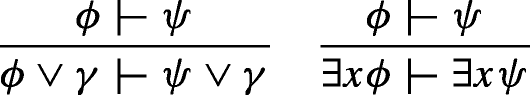
-
t-rule:
-
Enthymematic conditional:ϕ↦ψ := (ϕ ∧ t) → ψ
-
Set-theoretic axioms:
-
S1 \( x \in \{z : \phi (z)\} \leftrightarrow \phi (x)\) (abstraction)
-
S2 \( \forall z (z \in x \leftrightarrow z \in y) \leftrightarrow x = y\) (extensionality)
-
-
Induction axiom:
Every recursively defined set satisfies induction.
-
Key fact 1: ([19, p. 77])Identity is an equivalence relation.
-
Key fact 2: ([19, p. 77]Sets that differ in membership are non-identical. An important instance of this fact is that ∃(x ∈ a ∧ x∉a) → a≠a, where a is any set.
-
Key fact 3:Footnote 1Where f is some function,

-
Key fact 4: ([19, p. 85]On≠On
Rights and permissions
About this article
Cite this article
McAllister, I. Classical Logic is not Uniquely Characterizable. J Philos Logic 51, 1345–1365 (2022). https://doi.org/10.1007/s10992-021-09633-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-021-09633-5



 , stated as proposition 5.10 in [
, stated as proposition 5.10 in [