No CrossRef data available.
Article contents
Two questions from Dana Scott: Intuitionistic topologies and continuous functions
Published online by Cambridge University Press: 12 March 2014
Extract
Since intuitionistic sets are not generally stable – their membership relations are not always closed under double negation – the open sets of a topology cannot be recovered from the closed sets of that topology via complementation, at least without further ado. Dana Scott asked, first, whether it is possible intuitionistically for two distinct topologies, given as collections of open sets on the same carrier, to share their closed sets. Second, he asked whether there can be intuitionistic functions that are closed continuous in that the inverse of every closed set is closed without being continuous in the usual, open sense. Here, we prove that, as far as intuitionistic set theory is concerned, there can be infinitely-many distinct topologies on the same carrier sharing a single collection of closed sets. The proof employs Heyting-valued sets, and demonstrates that the intuitionistic set theory IZF [4, 624], as well as the theory IZF plus classical elementary arithmetic, are both consistent with the statement that infinitely many topologies on the set of natural numbers share the same closed sets. Without changing models, we show that these formal theories are also consistent with the statement that there are infinitely many endofunctions on the natural numbers that are closed continuous but not open continuous with respect to a single topology.
For each prime k ∈ ω, let Ak be this ω-sequence of sets open in the standard topology on the closed unit interval: for each n ∈ ω,
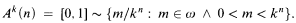
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2009




