Energy-Time Uncertainty Relations in Quantum Measurements

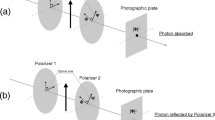
Abstract

Quantum measurement is a physical process. A system and an apparatus interact for a certain time period (measurement time), and during this interaction, information about an observable is transferred from the system to the apparatus. In this study, we quantify the energy fluctuation of the quantum apparatus required for this physical process to occur autonomously. We first examine the so-called standard model of measurement, which is free from any non-trivial energy–time uncertainty relation, to find that it needs an external system that switches on the interaction between the system and the apparatus. In such a sense this model is not closed. Therefore to treat a measurement process in a fully quantum manner we need to consider a “larger” quantum apparatus which works also as a timing device switching on the interaction. In this setting we prove that a trade-off relation (energy–time uncertainty relation), $\tau \cdot \Delta H_A \ge \frac{\pi \hbar }{4}$, holds between the energy fluctuation $\Delta H_A$ of the quantum apparatus and the measurement time $\tau$. We use this trade-off relation to discuss the spacetime uncertainty relation concerning the operational meaning of the microscopic structure of spacetime. In addition, we derive another trade-off inequality between the measurement time and the strength of interaction between the system and the apparatus.

Appendices

Appendix 1: Proof of Theorem 4

Proof

For simplicity, we assume that $t_0=0$ and that $\sigma (0)(=|\phi (0)\rangle \langle \phi (0))|$ is pure. Let us consider two states $\Theta _0(0)$ and $\Theta _t(0)$ $(0\le t\le \frac{\pi \hbar }{2 \Delta H_c})$ defined by

$$\begin{aligned} \Theta _0(0):= & {} \rho (0)\otimes |\phi (0)\rangle \langle \phi (0)| \\ \Gamma _t(0):= & {} \rho (0) \otimes |\phi (-t)\rangle \langle \phi (-t)|. \end{aligned}$$

These states evolve with the Hamiltonian $H=H_S+H_A+V$. Let us denote the states at time t by $\Theta _0(t)$ and $\Gamma _t(t)$. While $\Theta _0(t)$ may have a complicated form, $\Gamma _t(t)$ has a simple form,

$$\begin{aligned} \Gamma _t(t)=\rho ^0(t)\otimes |\phi (0)\rangle \langle \phi (0)|, \end{aligned}$$

where we used Lemma 2. Because the fidelity between two states is invariant under unitary evolution [15], it follows that

$$\begin{aligned} F(\Theta _0(0), \Gamma _t(0)) =F(\Theta _0(t), \Gamma _t(t)). \end{aligned}$$

The left-hand side of the above equation becomes

$$\begin{aligned} F(\Theta _0(0), \Gamma _t(0)) =|\langle \phi (0)| \phi (-t)\rangle | \end{aligned}$$

and the right-hand side is bounded as

$$\begin{aligned} F(\Theta _0(t), \Gamma _t(t))\le F(\rho (t), \rho ^0(t)), \end{aligned}$$

where we utilized the fact that the fidelity decreases for restricted states [15]. Thus it holds that

$$\begin{aligned} |\langle \phi (0)|\phi (-t)\rangle |\le F(\rho (t),\rho ^0(t)). \end{aligned}$$

The left-hand side of this inequality represents the speed of time evolution of the apparatus and is bounded. Let us fix a value $0 \le F_0 \le 1$ and denote by $\tau _F$ the minimum time t attaining $F(\rho (t), \rho ^0(t)) \le F_0$. Then we obtain,

$$\begin{aligned} \tau _{F_0} \cdot \Delta _{\alpha }(H) \ge 2 \hbar \arccos \frac{F_0 + 1-\alpha }{\alpha }. \end{aligned}$$

For this process to describe a measurement process, there must be an initial state attaining $F(\rho (t), \rho ^(0))\le \frac{1}{\sqrt{2}}$. Thus we obtain

$$\begin{aligned} \tau \cdot \Delta _{\alpha }(H) \ge 2 \hbar \arccos \frac{\frac{1}{\sqrt{2}}+ 1 -\alpha }{\alpha }. \end{aligned}$$

$\square$

Corollary 2

For $\alpha = \frac{1}{2}\left( \frac{1}{\sqrt{2}}+1\right)$, it holds that

$$\begin{aligned} \tau \cdot \Delta _{\alpha }(H) \ge \frac{2 \pi \hbar }{3}. \end{aligned}$$

Appendix 2: Proof of Theorem 5

Proof

We mimic the proof of Theorem 3. We consider the dynamics from time $t=t_0$ to $t=t_0+\tau$. Suppose that 0 and 1 are possible outcomes. We consider two states $|0\rangle$ and $|1\rangle$ satisfying $P_0 |0\rangle = |0\rangle$, $P_1|0\rangle = 0$, $P_1|1\rangle = |1\rangle$, and $P_0|1\rangle =0$ and define $|\pm \rangle := \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle )$. We consider a pair of initial states $|\pm \rangle \langle \pm | \otimes \sigma (t_0)$. The states to be compared are $\rho _{\pm }:=\text{ tr }_{\mathcal {K}}[e^{-i \frac{H}{\hbar }\tau } (|\pm \rangle \langle \pm | \otimes \sigma (t_0)) e^{i \frac{H}{\hbar }\tau }]$. For an arbitrary operator $\mathsf {A}$ on the system, it holds that

$$\begin{aligned}&\Bigg |\text{ tr }\Bigg [e^{-i \frac{H}{\hbar }\tau } (|(+\rangle \langle + | - |-\rangle \langle - | )\otimes \sigma (t_0)) e^{i \frac{H}{\hbar }\tau } (\mathsf {A}\otimes \mathbf {1})\Bigg ]\Bigg | \\&\quad \le 2 \Vert \mathsf {A}\Vert \sum _n \langle 0 \otimes \phi (t_0)| e^{i \frac{H}{\hbar }\tau } (\mathbf {1}\otimes \mathsf {E}_n) e^{-i \frac{H}{\hbar }\tau }|0 \otimes \phi (t_0)\rangle ^{1/2} \langle 1 \otimes \phi (t_0)| e^{i \frac{H}{\hbar }\tau }\\&\qquad \times \,(\mathbf {1}\otimes \mathsf {E}_n) e^{-i \frac{H}{\hbar }\tau }|1 \otimes \phi (t_0)\rangle ^{1/2} \\&\quad = 2 \Vert \mathsf {A}\Vert \sum _n P(n||0\rangle \langle 0|)^{1/2} P(n | |1\rangle \langle 1|)^{1/2} \\&\quad = 2 \Vert \mathsf {A}\Vert \left( P(0||0\rangle \langle 0|)^{1/2} P(0||1\rangle \langle 1|)^{1/2} +P(1||0\rangle \langle 0|)^{1/2} P(1||1\rangle \langle 1|)^{1/2}\right. \\&\qquad \left. +\, \sum _{n \ne 0,1} P(n||0\rangle \langle 0|)^{1/2} P(n||1\rangle \langle 1|)^{1/2} \right) \\&\quad \le 2\Vert \mathsf {A}\Vert \left( P(0||1\rangle \langle 1|)^{1/2} +P(1||0\rangle \langle 0|)^{1/2} \right. \\&\left. \qquad +\left( \sum _{n\ne 0,1} P(n||0\rangle \langle 0|)\right) ^{1/2} \left( \sum _{n \ne 0,1}P(n||1\rangle \langle 1|)\right) ^{1/2}\right) \\&\quad \le 6\Vert A\Vert \sqrt{P_{error}}. \end{aligned}$$

Thus we obtain $D(\rho _+, \rho _-):= \sup _{\mathsf {A}: \Vert \mathsf {A}\Vert =1} | \text{ tr }[(\rho _+ -\rho _-)\mathsf {A}] | \le 6 \sqrt{P_{error}}$. To estimate the magnitude of this perturbation we consider unitary evolution governed by the Hamiltonian $H_S$. In time $\tau$, this “unperturbed” dynamics changes $|\pm \rangle$ to a pair of orthogonal states $|\pm '\rangle$ of the system. We then estimate $F(\rho _{+}, |+'\rangle \langle +'|)$ and $F(\rho _-, |-'\rangle \langle -'|)$. As $|\pm '\rangle$ are orthogonal, we have

$$\begin{aligned}&F(\rho _+, |+'\rangle \langle +'|)^2 + F(\rho _-, |-'\rangle \langle -'|)^2 \\&\quad = \langle +'| \rho _+|+'\rangle + \langle -'| \rho _- |-'\rangle \\&\quad = \langle +'|\rho _+ |+'\rangle + \langle -'|\rho _+|-'\rangle +\langle -'| \rho _- - \rho _+|-'\rangle \\&\quad \le \text{ tr }[\rho _+] + D(\rho _+, \rho _-) \\&\quad \le 1 + 6 \sqrt{P_{error}}. \end{aligned}$$

Thus we can conclude

$$\begin{aligned} \min \{ F(\rho , |+'\rangle \langle +'|), F(\rho , |-'\rangle \langle -'|)\} \le \sqrt{ \frac{1+6 \sqrt{P_{error}}}{2}}. \end{aligned}$$

We assume $F(\rho , |+'\rangle \langle +'|)\le \sqrt{ \frac{1+6 \sqrt{P_{error}}}{2}}$. Combining it with Theorem 2 by putting $\rho (t_0)=|+\rangle \langle +|$, we obtain

$$\begin{aligned} \cos \left( \frac{\tau \Delta H_A}{\hbar } \right) \le \sqrt{ \frac{1+6 \sqrt{P_{error}}}{2}}. \end{aligned}$$

This ends the proof. $\square$