Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Moschovakis, Yiannis N.
2010.
Classical descriptive set theory as a refinement of effective descriptive set theory.
Annals of Pure and Applied Logic,
Vol. 162,
Issue. 3,
p.
243.
Majcher-Iwanow, Barbara
2012.
Polish group actions and effectivity.
Archive for Mathematical Logic,
Vol. 51,
Issue. 5-6,
p.
563.
Marion, Jean-Yves
2012.
From Turing machines to computer viruses.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 370,
Issue. 1971,
p.
3319.
Jones, Neil D.
2013.
A Swiss Pocket Knife for Computability.
Electronic Proceedings in Theoretical Computer Science,
Vol. 129,
Issue. ,
p.
1.
Pavlovic, Dusko
2013.
Monoidal computer I: Basic computability by string diagrams.
Information and Computation,
Vol. 226,
Issue. ,
p.
94.
Abramsky, Samson
2014.
Johan van Benthem on Logic and Information Dynamics.
Vol. 5,
Issue. ,
p.
121.
Markose, Sheri M.
2016.
Complex Type 4 Structure Changing Dynamics of Digital Agents: Nash Equilibria of a Game with Arms Race in Innovations.
SSRN Electronic Journal,
Moschovakis, Yiannis N.
2016.
Martin Davis on Computability, Computational Logic, and Mathematical Foundations.
Vol. 10,
Issue. ,
p.
107.
M. Markose, Sheri
2017.
Complex type 4 structure changing dynamics of digital agents: Nash equilibria of a game with arms race in innovations.
Journal of Dynamics & Games,
Vol. 4,
Issue. 3,
p.
255.
Moschovakis, Joan R.
and
Moschovakis, Yiannis N.
2018.
Intuitionism and effective descriptive set theory.
Indagationes Mathematicae,
Vol. 29,
Issue. 1,
p.
396.
Pavlovic, Dusko
and
Yahia, Muzamil
2018.
Coalgebraic Methods in Computer Science.
Vol. 11202,
Issue. ,
p.
167.
TERWIJN, SEBASTIAAN A.
2018.
GENERALIZATIONS OF THE RECURSION THEOREM.
The Journal of Symbolic Logic,
Vol. 83,
Issue. 04,
p.
1683.
Barendregt, Henk
and
Terwijn, Sebastiaan A.
2019.
Fixed point theorems for precomplete numberings.
Annals of Pure and Applied Logic,
Vol. 170,
Issue. 10,
p.
1151.
SALEHI, SAEED
2020.
ON THE DIAGONAL LEMMA OF GÖDEL AND CARNAP.
The Bulletin of Symbolic Logic,
Vol. 26,
Issue. 1,
p.
80.
Terwijn, Sebastiaan A.
2020.
The noneffectivity of Arslanov’s completeness criterion and related theorems.
Archive for Mathematical Logic,
Vol. 59,
Issue. 5-6,
p.
703.
Weber, Zach
2021.
Paradoxes and Inconsistent Mathematics.
Tourlakis, George
2022.
Computability.
p.
281.
Kennedy, Juliette
2022.
Gödel's Incompleteness Theorems.
Salehi, Saeed
2022.
Tarski’s Undefinability Theorem and the Diagonal Lemma.
Logic Journal of the IGPL,
Vol. 30,
Issue. 3,
p.
489.
Golov, Anton
and
Terwijn, Sebastiaan A.
2022.
Fixpoints and relative precompleteness.
Computability,
Vol. 11,
Issue. 2,
p.
135.
 .
. for some e.
for some e. : Nm+1 → ℕ such that
: Nm+1 → ℕ such that .
. of (1+m+n) arguments with values in V, there is a total recursive function
of (1+m+n) arguments with values in V, there is a total recursive function  of m arguments such that
of m arguments such that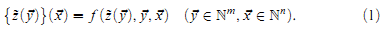
 and let
and let  .
.




