Optimal Control Strategies and Sensitivity Analysis of an HIV/AIDS-Resistant Model with Behavior Change

Abstract

Despite several research on HIV/AIDS, it is still incumbent to investigate more effective control measures to mitigate its infection level. Therefore, we introduce an HIV/AIDS-resistant model with behavior change and study its basic properties. In order to determine the most sensitive parameters that are responsible for disease transmission with respect to the basic reproduction number and those responsible for disease prevalence with respect to the endemic equilibrium, the sensitivity analysis was established and it was confirmed that the influx rate of people into the infected population and total abstinence from all risk practices and endemic areas are some of the most sensitive parameters for disease spread and disease eradication, respectively. Furthermore, by considering controls $u_1$ denoting the government’s intervention in promoting and encouraging behavior change, $u_2$ representing intake of balanced nutritional supplementation, and $u_3$ connoting antiretroviral therapy (ART), an optimal control problem was developed and analyzed. Before the establishment of the necessary conditions of the optimal control using Pontryagin’s Maximum Principle, we proved the existence of the optimal control triplet $(u_1(t),u_2(t),u_3(t)\in \Phi ,$ where $\Phi$ is the control set at time t,) which has been neglected by many researchers in recent years. Using the Runge–Kutta scheme, the optimal control problem was solved to understand the best combination of control strategies. Using the demographic and epidemiological data for South Africa on HIV/AIDS, a numerical simulation was carried out and results are presented on 3D surface plots. The obtained results suggested that the combination of all the considered control measures is the best method to ensure disease eradication.

1 Introduction

HIV infection has been a dangerous health hazard for people across the world for decades, and consequently claims millions of lives, especially in the resource-less and undeveloped countries. From the recent data of the World Health Organization (WHO), an estimated 36.7 million people were living with HIV, with approximately 2 million newly infected globally, and more than a million deaths due to its spread in 2015 (UNAIDS 2015). The two main types of HIV strains are HIV-1 and HIV-2. The most dangerous one that has spread worldwide is HIV-1, while the latter is less pathogenic and less spread, and therefore it is confined mainly to the West African countries. The tests carried out on one can not sufficiently detect the other due to large genetic differences between them.

Several factors account for the uneven global distribution of the HIV-1 virus incidence across the world. Some of these factors are political, social and economic, especially on the African continent. The epicenter of the disease is South Africa, some other countries in Sub-Sahara Africa are neither spared from the spread. Out of over millions of infected adults and children around the world, more than 70% of them are from sub-Sahara Africa, of which over 32% resides in Southern African countries such as Botswana, Lesotho, Swaziland etc. (HIV 2018; Phillips and Pirkle 2011).

Unfortunately, no substantial treatment of HIV/AIDS has been discovered. An alternative treatment that can guarantee viral suppression, reduction in morbidity and mortality rate is the antiretroviral treatment (ART). However, it does not ensure complete eradication of the virus from the blood stream. To achieve this objective and ensure complete treatment, perfect vaccine and medicinal drugs are still much needed (Simon et al. 2006).

The threat of HIV/AIDS seems unassailable. However, several preventive strategies have been identified, and effect of behavior change has been highly recognized and acknowledged. Behavior change is is about modifying behaviors that lower the probabilities of disease transmission and chronic illness, and maintain disease management (Coleman and Pasternak 2012). This includes the process of conducting actions that encourage positive behavior and alter negative behavior, or application of different types of intervention strategies which can be achieved through motivational and educational techniques by targeting some specific groups of people or particular individuals (Coates et al. 2008). The positive impacts of behavior change strategy have been recorded for a big reduction in HIV infections. The ABC-approach, which simply means advocating abstinence, being faithful and consistent condom usage, has been identified as the most common behavior change strategy (Shelton et al. 2004).

According to (Report 2012), appearance of new HIV/AIDS infection cases has been drastically reduced in the majority of Southern African countries. For example, behavior change such as reduction of sexual partners, delay of the onset of sexual intercourse, and increase in condom usage accounts for 73% reduction of infection in Malawi, 71% in Botswana, 68% in Namibia, 58% in Zambia, 50% in Zimbabwe and 41% in South Africa. Those who show partial abstinence are those that only reduce their sexual partners but still live in an endemic environment, while those who totally abstain are those who maintain only one sexual partner and do away from all endemic or exposed environments.

Some category of people develop resistance to HIV/AIDS (Marmor et al. 2006; Paxton et al. 1996; Samson et al. 1996). The resistance can be in the form of an exposed uninfected scenario which has been identified among health workers, prostitutes and infants of infected mothers. The other scenario is the case of infected individuals with slow or no progression to AIDS without any medication or treatment. They live for years with the virus with insignificant or no loss of CD4+ cells (Easterbrook 1999; Marmor et al. 2006), as may be expected to occur under healthy circumstances.

The 2014 report (Green 2015) established that some people show partial or total inborn resistance to HIV/AIDS. The possible reasons behind this strange occurrences have been studied by (Altman 2000; Blackwell 2012; Mendus and Ring 2016; Singh 2015; Minnesota 2014). Just a decade ago, it was opined that acute-phase amyloid A protein, interleukin-22, Toll-like receptors, natural killer cells and some other proteins may be the reason why some infected individuals do not seroconvert let alone progress to AIDS despite multiple exposure to HIV (Biasin et al. 2010). These individuals live a normal life because the virus cannot bind itself together, and perhaps it is here that the key to overcome the infection lies.

Despite the implementation of ART in sub-Saharan Africa for the past few years, the mortality rate of HIV/AIDS is still alarming, especially in the first few months of the treatment. One of the major identified reasons is poor nutrition otherwise called malnutrition. Few patients who maintain a balanced nutritional supplementation have improved prognosis (Braitstein et al. 2006; Koethe et al. 2010; Olsen et al. 2014). Nutritional support with balanced optimal composition has become a key factor in the ART program and it is needed in abundance to be distributed among the infected and less privileged patients who constitute the poorest of the poor community in some African countries to reduce the mortality rate (Grobler et al. 2013; Lamb et al. 2012).

Researchers such as in Jeremiah et al. (2014), Polasa et al. (1984) discovered that nutritional deficiency hinders the effectiveness of pharmacokinetics, such as rifampin which is identified as the most effective drug for HIV-tuberculosis (HIV-TB) co-infected patients. Frequent intake of balanced nutritional supplementation leads to increase in body weight and decreases mortality rate during the infection and treatment period.

The essence of optimal control is inestimable in mathematical modeling. This is the analysis that shows the best combination of control strategies that ensure reduction in the spread of infectious diseases. This analysis has been studied by many researchers such as (Makinde and Okosun 2011; Ngina et al. 2019; Okosun et al. 2013, 2013). Few researchers have proved the existence of the optimal control variables, in fact, to the best of our knowledge, it has only been proved by Ngina et al. (2019) in their within-host and drug-resistant model. We shall employ the same approach to establish the existence of our optimal control variables, which is a new element in the study of HIV/AIDS models.

Several mathematical models on HIV/AIDS are readily available online, but optimal control and sensitivity analyses of an HIV/AIDS model with resistance and behavior change still pose an unanswered biological question that we will like to address in this work. The available works that examined the effects of resistance are (Jia and Xiao 2018; Khanh 2016; Rabiu et al. 2020), where all of them incorporated it in flu model which is very much different from this study. Uniquely, our model also incorporates time-dependent controls (government’s intervention in promoting and encouraging behavior change, intake of balanced nutritional supplementation and ART) to determine the best combination of strategies capable in dealing with the virus spread.

A mathematical modeling approach shall be used to study the dynamics, sensitivity analysis and optimal control analysis of an HIV/AIDS-resistant model with behavior change. In order to contribute to the work of the aforementioned researchers, we developed a new model as follows:

• 1. We incorporate the susceptible class (S) and the class of susceptibles with behavior change $(S_b)$. We also include classes $(I_1)$ and $(I_{1b})$ for slow progressors and slow progressors with behavior change, respectively. They are considered to have partial resistance to the virus. Classes $(I_2)$ and $(I_{2b})$ for non progressors and non progressors with behavior change respectively, are also incorporated. They are considered to have complete resistance to the virus and do not progress to the AIDS compartment (A). We finally include classes $(I_3)$ and $(I_{3b})$ for fast progressors and fast progressors with behavior change, respectively. They are considered to have no resistance to the virus.

• 2. We calculate the sensitivity analysis indices to determine the most sensitive parameters that are responsible for disease transmission with respect to the basic reproduction number, and those responsible for disease prevalence with respect to the endemic equilibrium.

• 3. We apply optimal controls to the model to determine the combined effects of the control triplet $u_1(t),u_2(t),u_3(t)$.

• 4. The proof of existence of the optimal control variables, which has been largely neglected by many researchers, is also established.

• 5. We examine the effect of the control variables on the control reproduction number.

The work is arranged as follows. Section 2 contains model formulation and parameter description, while Sect. 3 entails the model and its basic properties. The sensitivity analysis of the model is discussed in Sect. 4. Furthermore, we solve the optimal control problem and prove the necessary conditions and uniqueness of the control variables in the same section. Section 5 presents numerical solutions and graphical representations of the obtained results. The concluding remarks, acknowledgment, disclosure statement, and conflict of interest follow in Sect. 6.

2 Model Formulation and Assumptions

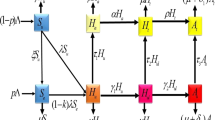
We formulate a model of HIV resistance and behavior change by splitting the total human population at time t, denoted by N(t), into nine mutually-exclusive compartments of susceptible individuals S(t),  susceptible individuals with behavior change $S_b(t),$ slow progressors HIV-1 $I_1(t)$, slow progressors HIV-1 with behavior change $I_{1b}(t)$, non progressors HIV-1 $I_2(t)$, non progressors HIV-1 with behavior change $I_{2b}(t)$, fast progressors HIV-1 $I_3(t)$, fast progressors HIV-1 with behavior change $I_{3b}(t)$, and AIDS class A such that

$$\begin{aligned} N(t)=S(t)+S_{b}(t)+I_1(t)+I_{1b}(t)+I_2(t)+I_{2b}+I_3(t)+I_{3b}+A(t). \end{aligned}$$

We assume that the AIDS class consists of weak and unhealthy infected individuals that are sexually inactive.

Sexually active individuals are recruited into the susceptible population at a constant rate B. The susceptible individuals acquire the virus through effective contact with HIV-1 positive and infectious individuals at the rate $\lambda$ (known as force of infection) given by

$$\begin{aligned} \lambda =\frac{\beta (I_3+\sigma _1I_{3b}+\sigma _2I_2+\sigma _3I_{2b}+\sigma _4I_1+\sigma _5I_{1b})}{N}, \end{aligned}$$

(1)

where $\beta$ in (1) denotes the effective contact rate that is capable of leading to infection, $0\le \sigma _1,\sigma _2,\sigma _3,\sigma _4,\sigma _5\le 1$ denote the modification parameters that account for the assumed reduction in the transmission of virus by the various HIV-1 infected classes.

The acquisition of infection by slow, non and fast progressors HIV-1 individuals $I_1,I_2$ and $I_3$ occurs at the rates $\alpha _1\lambda ,\alpha _2\lambda$ and $\alpha _3\lambda$ respectively, while natural death occurs at a constant rate $\mu$. The susceptible individuals in class S change their sexual behavior through total abstinence at a rate $\gamma _1$. The individuals in $S_b$ become reckless and regress to S at a rate $\gamma _2$. Individuals in $S_b$ are assumed to have no contacts with infectious individuals due to total behavior change. Therefore, the rate of change of the total population of both susceptible and susceptible with behavior change classes is respectively given by

$$\begin{aligned} \dot{S}(t)=\,&B-(\alpha _1+\alpha _2+\alpha _3)\lambda S+\gamma _2S_b-(\mu +\gamma _1) S,\\ \dot{S_b}(t)=\,&\gamma _1S-(\gamma _2+\mu )S_b, \end{aligned}$$

where $^{\cdot }$ represents derivative with respect to time.

The slow-progressor HIV-1 infected class $I_1$ is generated by the break-through of infection of susceptible class at the rate $\alpha _1\lambda$. A fraction of this category of people abstains totally from HIV-1 (due to the change of behavior) and then progresses to $I_{1b}$ at the rate $\gamma _3$. Those who abstain partially (that is those who are reckless) may regress back to $I_1$ at the rate $\gamma _4$. This compartment also contains those who slowly progress to AIDS (due to the partial resistance to AIDS) at the rate $\rho _1$ so that the governing equations are:

$$\begin{aligned}&\dot{I_1}(t)=\alpha _1\lambda S+\gamma _4I_{1b}-(\gamma _3+\mu +\rho _1)I_1,\\&\dot{I_{1b}}(t)=\gamma _3I_1-(\gamma _4+\mu )I_{1b}. \end{aligned}$$

Similarly, we compose the non-progressor HIV-1 infected class $I_2$ by the break-through of infection of susceptible class at the rate $\alpha _2\lambda$. A fraction of this category of people abstains totally from HIV-1 (due to the change of behavior) and then progresses to $I_{2b}$ at the rate $\gamma _5$. Those who abstain partially (that is those who are reckless) may regress back to $I_2$ at the rate $\gamma _6$. This compartment does not contain those who progress to AIDS due to their full resistance to AIDS, so that the governing equations are:

$$\begin{aligned}&\dot{I_2}(t)=\alpha _2\lambda S+\gamma _6I_{2b}-(\gamma _5+\mu )I_2,\\&\dot{I_{2b}}(t)=\gamma _5I_2-(\gamma _6+\mu )I_{2b}. \end{aligned}$$

The fast-progressor HIV-1 infected class $I_3$ is generated by the break-through of infection of susceptible class at the rate $\alpha _3\lambda$. A fraction of this category of people abstains totally from HIV-1 (due to the change of behavior) and then progresses to $I_{3b}$ at the rate $\gamma _7$. Those who abstain partially (that is those who are reckless) may regress back to $I_3$ at the rate $\gamma _8$. This compartment also contains those who progress fast to AIDS at the rate $\rho _2$ (because they have no resistance to AIDS) so that the governing equations are:

$$\begin{aligned}&\dot{I_3}(t)=\alpha _3\lambda S+\gamma _8I_{3b}-(\gamma _7+\mu +\rho _2)I_3,\\&\dot{I_{3b}}(t)=\gamma _7I_3-(\gamma _8+\mu )I_{3b}. \end{aligned}$$

Taking $\tau$ to be the disease-induced death rate, the AIDS class dynamics is given by

$$\begin{aligned} \dot{A}(t)=\rho _1I_1+\rho _2I_3-(\mu +\tau )A. \end{aligned}$$

We assume that the transfers of infections from susceptibles to the classes $I_1, I_2$ and $I_3$ are different; so that we have

$$\begin{aligned} 0\le \alpha _2<\alpha _1<\alpha _3<1~\text {and}~\alpha _1+\alpha _2+\alpha _3=1. \end{aligned}$$

(2)

The resultant mathematical model is given by:

$$\begin{aligned} \dfrac{dS}{dt}=\,&B-(\alpha _1+\alpha _2+\alpha _3)\lambda S+\gamma _2S_b-K_1S, \end{aligned}$$

(3)

$$\begin{aligned} \dfrac{dS_b}{dt}=\,&\gamma _1S-K_2S_b,\end{aligned}$$

(4)

$$\begin{aligned} \dfrac{dI_1}{dt}=\,&\alpha _1\lambda S+\gamma _4I_{1b}-K_3I_1,\end{aligned}$$

(5)

$$\begin{aligned} \dfrac{dI_{1b}}{dt}=\,&\gamma _3 I_1-K_4I_{1b},\end{aligned}$$

(6)

$$\begin{aligned} \dfrac{dI_2}{dt}=\,&\alpha _2\lambda S+\gamma _6 I_{2b}- K_5I_2,\end{aligned}$$

(7)

$$\begin{aligned} \dfrac{dI_{2b}}{dt}=\,&\gamma _5 I_2-K_6I_{2b},\end{aligned}$$

(8)

$$\begin{aligned} \dfrac{dI_3}{dt}=\,&\alpha _3\lambda S+\gamma _8I_{3b}-K_7I_3,\end{aligned}$$

(9)

$$\begin{aligned} \dfrac{dI_{3b}}{dt}=\,&\gamma _7 I_3-K_8I_{3b},\end{aligned}$$

(10)

$$\begin{aligned} \dfrac{dA}{dt}=\,&\rho _1I_1+\rho _2I_3-K_9A, \end{aligned}$$

(11)

where

$$\begin{aligned}&K_1=\gamma _1+\mu , K_2=\gamma _2+\mu , K_3=\gamma _3+\mu +\rho _1, K_4=\gamma _4+\mu , \\&K_5=\gamma _5+\mu ,K_6=\gamma _6+\mu , K_7=\gamma _7+\mu +\rho _2, K_8=\gamma _8+\mu ,K_9=\mu +\tau , \end{aligned}$$

with initial condition

$$\begin{aligned}&S(0)\ge 0, S_b(0)\ge 0,I_1(0)\ge 0,I_{1b}(0)\ge 0,I_2(0)\ge 0,I_{2b}(0)\ge 0,\nonumber \\&I_3(0)\ge 0,I_{3b}(0)\ge 0,A(0)\ge 0. \end{aligned}$$

(12)

The flow chart of this model is given below (Fig. 1).

Fig. 1

Flow chart of the model

3 Analysis of the Model

3.1 Basic Properties of the Model

Here, we shall establish that the mathematical model (3)–(11) is epidemiologically feasible. This can be done by establishing that the populations remain non-negative, which means we need to prove that all the solutions of the model with positive initial conditions are non-negative at all time $t>0$. We assume that the initial conditions at the onset of the HIV-1 disease outbreak is given by (12).

We define a region

$$\begin{aligned} \Sigma =\left\{ (S,S_{b},I_1,I_{1b},I_2,I_{2b},I_3,I_{3b},A)\in \mathfrak {R}_+^9:0<N\le \frac{B}{\mu } \right\} . \end{aligned}$$

(13)

Theorem 3.1

The feasible region $\Sigma$ with initial conditions presented in ( 12 ) is positively invariant and attracting.

Proof

Since $N>0$ in $\Sigma$, so the force of infection $\lambda$ is well-defined, and since the right-hand side of (3)–(11) is Liptschitzian, differentiable and continuous with partial derivatives defined in $\Sigma$, the Picard Theorem (Dass 2008) provides the existence of solutions on some interval $[0,\Theta )$ where $0<\Theta \le \infty$ depends on (12). It can be easily observed that

$$\begin{aligned}&\dot{S}\ge 0~\text {if}~S=0,\dot{S}_b\ge 0~\text {if}~S_b=0,\dot{I}_1\ge 0~\text {if}~I_1=0,\dot{I}_{1b}\ge 0~\text {if}~I_{1b}=0,\\&\dot{I}_2\ge 0~\text {if}~I_2=0,\dot{I}_{2b}\ge 0~\text {if}~I_{2b}=0,\dot{I}_{3}\ge 0~\text {if}~I_{3}=0,\dot{I}_{3b}\ge 0~\text {if}~I_{3b}=0,\\&\dot{A}\ge 0~\text {if}~A=0. \end{aligned}$$

Therefore, from the provision of (12), the solutions $S(t),S_b(t),I_1(t), I_{1b}(t), I_2(t),I_{2b}(t),I_3(t),I_{3b}(t),A(t)$ are non-negative in the interval $[0,\Theta )$.

Consequently, adding (3)–(11) together gives

$$\begin{aligned} \frac{dN}{dt}=B-\mu N-\tau A\le B-\mu N, \end{aligned}$$

(14)

whose solution satisfies

$$\begin{aligned}&N(t)\le \frac{B}{\mu }+\left[ N(0)-\frac{B}{\mu }\right] \exp {(-\mu t)}, \nonumber \\&\quad \lim _{t\rightarrow \infty }N(t)\le \frac{B}{\mu }+\lim _{t\rightarrow \infty }\left[ N(0)-\frac{B}{\mu }\right] \exp {(-\mu t)}\le \frac{B}{\mu },\nonumber \\&\quad \lim _{t\rightarrow \infty }N(t)\le \frac{B}{\mu }. \end{aligned}$$

(15)

This confirms that the solution is bounded above by $\frac{B}{\mu }$ in the domain defined by (13). Therefore, the model is epidemically well-posed and meaningful since all the state variables are non-negative for all $t\ge 0$ (Djomegni et al. 2020; Rabiu et al. 2020, 2020; Rabiu and Akinyemi 2016) . Hence, $\Sigma$ is a feasible region and it is sufficient to study the model in $\Sigma$. This completes the proof. $\square$

3.2 Disease-Free Equilibrium and Its Stability

The disease-free equilibrium is defined as the point where no virus is present in the community. The equilibrium will show the behavior of the model in the absence of HIV-1 virus. It is worth noting here that since the susceptible individuals are uninfected, their change of behavior should be through total abstinence from all activities that can lead to HIV/AIDS contraction and not partial abstinence. It is only the infected individuals that can choose whether to abstain totally or partially. For this case, $\gamma _2$ for partial abstinence will be zero, while $\gamma _1$ for total abstinence will not be equal to zero. For the system of Eqs. (3)–(11), only the compartments S and $S_{b}$ are involved with uninfected individuals, while others ($I_1=I_{1b}=I_2=I_{2b}=I_3=I_{3b}=A=0$) are the infected ones. Hence, the disease-free equilibrium of (3)–(11) is given by

$$\begin{aligned} \Psi ^*=(S^*, S^*_b,I_1^*,I_{1b}^*,I_2^*,I_{2b}^*,I_3^*,I_{3b}^*,A^*)=\left( \frac{B}{\mu +\gamma _1},\frac{\gamma _1B}{\mu (\gamma _1+\mu )},0,0,0,0,0,0,0\right) . \end{aligned}$$

(16)

But if we assume they abstain both partially and totally (i.e $\gamma _1\ne 0,\gamma _2\ne 0$), then the disease-free equilibrium of (3)–(11) becomes

$$\begin{aligned} \Psi ^*_c=(S^*, S^*_b,I_1^*,I_{1b}^*,I_2^*,I_{2b}^*,I_3^*,I_{3b}^*,A^*)=\left( \frac{BK_2}{K_1K_2-\gamma _1\gamma _2},\frac{\gamma _1B}{K_1K_2-\gamma _1\gamma _2},0,0,0,0,0,0,0\right) . \end{aligned}$$

(17)

Note that for the subsequent analyses, Eq. (16) shall be used and $\gamma _2$ shall be set to zero, so that $K_2=\mu$.

Employing the next generation method (Diekmann et al. 1990; Van den Driessche and Watmough 2002) to Eqs. (3)–(11), $\mathcal {F}$ (the new infection terms) and $\mathcal {V}$ (transfer terms) are expressed as

$$\begin{aligned}&\mathcal {V}= \left[ \begin{array}{ccccccc} K_3&{}-\gamma _4&{}0&{}0&{}0&{}0&{}0\\ -\gamma _3&{}K_4&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}K_5&{}-\gamma _6&{}0&{}0&{}0\\ 0&{}0&{}-\gamma _5&{}K_6&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}K_7&{}-\gamma _8&{}0\\ 0&{}0&{}0&{}0&{}-\gamma _7&{}K_8&{}0\\ -\rho _1&{}0&{}0&{}0&{}-\rho _2&{}0&{}K_9\\ \end{array} \right] , \\&\mathcal {F}=\left[ \begin{array}{ccccccc} \dfrac{\alpha _1\beta \sigma _4\mu }{K_1}&{}\dfrac{\alpha _1\beta \sigma _5\mu }{K_1}&{}\dfrac{\alpha _1\beta \sigma _2\mu }{K_1}&{}\dfrac{\alpha _1\beta \sigma _3\mu }{K_1}&{}\dfrac{\alpha _1\beta \mu }{K_1}&{}\dfrac{\alpha _1\beta \sigma _1\mu }{K_1}&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ \dfrac{\alpha _2\beta \sigma _4\mu }{K_1}&{}\dfrac{\alpha _2\beta \sigma _5\mu }{K_1}&{}\dfrac{\alpha _2\beta \sigma _2\mu }{K_1}&{}\dfrac{\alpha _2\beta \sigma _3\mu }{K_1}&{}\dfrac{\alpha _2\beta \mu }{K_1}&{}\dfrac{\alpha _2\beta \sigma _1\mu }{K_1}&{}0\\ \\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ \dfrac{\alpha _3\beta \sigma _4\mu }{K_1}&{}\dfrac{\alpha _3\beta \sigma _5\mu }{K_1}&{}\dfrac{\alpha _3\beta \sigma _2\mu }{K_1}&{}\dfrac{\alpha _3\beta \sigma _3\mu }{K_1}&{}\dfrac{\alpha _3\beta \mu }{K_1}&{}\dfrac{\alpha _3\beta \mu \sigma _1}{K_1}&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ \end{array} \right] . \end{aligned}$$

Using $\rho$ as the spectral radius (magnitude of the dominate eigenvalue) of the next generation matrix $\mathcal {F}\mathcal {V}^{-1}$, then $\rho (\mathcal {F}\mathcal {V}^{-1})$ is given by

$$\begin{aligned}&\mathcal {R}_T= \frac{\beta \alpha _1\mu (\sigma _4K_4+\sigma _5\gamma _3)}{K_1(K_3K_4-\gamma _3\gamma _4)}+\frac{\beta \alpha _2\mu (\sigma _2K_6+\sigma _3K_5)}{K_1(K_5K_6-\gamma _5\gamma _6)}+\frac{\beta \alpha _3\mu (K_8+\gamma _7\sigma _1)}{K_1(K_7K_8-\gamma _7\gamma _8)}. \end{aligned}$$

(18)

The threshold parameter $\mathcal {R}_T$ is the reproduction number of (3)–(11). It is used in measuring the average number of new HIV infections generated by a single infected individual introduced into a community/population where a certain fraction of the population changed their behavior towards HIV-1 infection by using condom, being faithful to one partner, etc. Hence, we present the following Lemma.

Lemma 3.2

The disease-free equilibrium point (DFE) of the model is locally asymptotically stable (LAS) if $\mathcal {R}_T<1$ , and unstable when $\mathcal {R}_T>1.$

The biological implication of Lemma 3.2 is that, when the reproduction number is less than unity, the infection will die out in the community quickly, thereby making the disease-free equilibrium stable. On the other hand, when the reproduction number is greater than unity, the whole community will be infected quickly since more than 1 person will be contracting the infection on a daily basis. This makes the disease-free equilibrium unstable.

3.3 Existence of Endemic Equilibrium

The model has a unique positive endemic equilibrium point (EEP). This is the point where at least one of the virus infected compartments is non-zero. Let

$$\begin{aligned} \Psi ^{**}=(S^{**},S^{**}_b,I_1^{**},I_{1b}^{**},I_2^{**},I_{2b}^{**},I_3^{**},I_{3b}^{**},A^{**}), \end{aligned}$$

(19)

be the endemic equilibrium point. We further define the force of infection as

$$\begin{aligned} \lambda ^{**}=\frac{\beta (I_3^{**}+\sigma _1I_{3b}^{**}+\sigma _2I_2^{**}+\sigma _3I_{2b}^{**}+\sigma _4I_1^{**}+\sigma _5I_{1b}^{**})}{N^{**}}. \end{aligned}$$

(20)

Solving Eq. (3)–(11) in terms of the force of infection $\lambda ^{**}$ at steady-state as follows:

$$\begin{aligned}&S^{**}=\frac{BK_2}{K_2(f_1\lambda ^{**}+K_1)},I_{1}^{**}=\frac{\alpha _1\lambda ^{**}BK_2K_4}{K_2(K_3K_4-\gamma _3\gamma _4)(f_1\lambda ^{**}+K_1)}, \nonumber \\&I_{1b}^{**}=\frac{\alpha _1\lambda ^{**}BK_2\gamma _3}{K_2(K_3K_4-\gamma _3\gamma _4)(f_1\lambda ^{**}+K_1)},S^{**}_b=\frac{B\gamma _1}{K_2(f_1\lambda ^{**}+K_1)}, \nonumber \\&I_2^{**}=\frac{B\alpha _2K_2K_6\lambda ^{**}}{W_5K_2(f_1\lambda ^{**}+K_1)},I_{2b}^{**}=\frac{B\alpha _2K_2\gamma _5\lambda ^{**}}{W_5K_2(f_1\lambda ^{**}+K_1)},\nonumber \\&I_3^{**}=\frac{B\alpha _3K_2K_8\lambda ^{**}}{W_7K_2(f_1\lambda ^{**}+K_1)},I_{3b}^{**}=\frac{B\alpha _3K_2\gamma _7\lambda ^{**}}{W_7K_2(f_1\lambda ^{**}+K_1)},\nonumber \\&A^{**}=\frac{(\alpha _1\rho _1K_4W_7+\alpha _3K_8\rho _2W_3)\lambda ^{**}BK_2}{K_9W_3W_7K_2(f_1\lambda ^{**}+K_1)}, \nonumber \\&N^{**}=\frac{BK_9W_3W_7[K_2(f_1\lambda ^{**}+K_1)]-\tau \lambda ^{**}BK_2[(\alpha _1\rho _1K_4W_7+\alpha _3K_8\rho _2W_3)]}{ K_9W_3W_7K_2(f_1\lambda ^{**}+K_1)}, \end{aligned}$$

(21)

where

$$\begin{aligned}&f_1=\mu +(\alpha _1+\alpha _2+\alpha _3)\lambda ^{**},W_3=K_3K_4-\gamma _3\gamma _4,\nonumber \\&W_5=K_5K_6-\gamma _5\gamma _6,W_7=K_7K_8-\gamma _7\gamma _8. \end{aligned}$$

(22)

Substituting all the equations in (21) into (20), it can be shown that the non-zero equibria of the model satisfy the following linear equation in terms of $\lambda ^{**}$:

$$\begin{aligned} a_2\lambda ^{**}+a_3=0, \end{aligned}$$

(23)

where

$$\begin{aligned} a_2&=W_5W_7K_2\alpha _1(W_3K_9-\tau K_4\rho _1)+\alpha _3W_3W_5K_2(W_7K_9-K_8\rho _2\tau )\nonumber \\&\quad +W_3W_5W_7K_2K_9\alpha _2>0,\nonumber \\ a_3&=K_9W_1W_3W_5W_7\left( 1-\mathcal {R}_T \right) , \end{aligned}$$

(24)

where $W_1=K_1K_2$.

Obviously, $a_2>0$, $a_3\ge 0$ if and only if $\mathcal {R}_T\le 1$ so that $\lambda ^{**}=-\frac{a_3}{a_2}\le 0$, which shows no existence of a positive endemic equilibrium whenever $\mathcal {R}_T\le 1$. Hence, the endemic equilibrium point $\Psi ^{**}$ exists and is unique whenever $\mathcal {R}_T>1.$ We claim the following result.

Lemma 3.3

The endemic equilibrium point (EEP) of the model ( 3 )–( 9 ) is locally asymptotically stable (LAS) if $\mathcal {R}_T>1.$

3.4 Parameter Estimation and Sensitivity Analysis

In this section, we shall carryout the sensitivity analysis of the model parameters (Awan et al. 2018; Marsudi and Andari 2014; Tchuenche et al. 2011). This analysis will save time, money and energy in our effort to curtail the spread by focusing squarely on the most sensitive parameters for both disease transmission and prevalence. Since the basic reproduction number causes initial disease transmission and endemic equilibrium causes disease prevalence, we shall focus on parameters in the basic reproduction number and the endemic equilibrium of the non-behavior change infected classes. This is because the non-behavior change infected classes are more dangerous than those that do not change behavior.

The South African mid-year population estimates of 2019 (South 2019) shall be used to estimate our parameter values and the initial conditions for each population class. Since our model is an HIV-1 model incorporating behavior change, only those who are mature and sexually active are involved. For this reason, we shall only focus on data of people within the age bracket 15–49 years as appeared in the statistical report.

The simple rationale behind the fact that we took South Africa as a case study is that, in 2018, South Africa was ranked 4th behind Botswana (21.90%), Lesotho (25.00%) and Eswatini (Swaziland) (27.20%) as the country with highest HIV/AIDS prevalence rate with 18.90% of the population affected (countries yyy). The more alarming issue is the fact that the HIV/AIDS population of South Africa only (7,060,000) is higher than the total population of Swaziland (1,136,191), Botswana (2,254,126) and Lesotho (2,108,132) ac- cording to the 2018 report in Population (2018). We therefore see South Africa as a suitable country to be taken as a case study. The South African population as at 2019 was estimated at 58,775,022 among which the mature and sexually active population within the age 15–49 is given by 31,842,922. This gives the initial condition $S(0) = 31, 842, 922$.

The calculated HIV prevalence rate is approximately 13.5% of the South African population. The total number of HIV infected individuals is approximately 7,970,000 in the year 2019. For the age group 15–49, 19.07% of 7,970,000 which is 1,519,879 is HIV positive. Since the data doesn’t differentiate between the rate of progression of the infected classes, we divide the 1,519,879 between $I_1$, $I_2$ and $I_3$ as $I_1(0) = 350,000$, $I_{2}(0) = 519,879$ and $I_3(0) = 650,000$. More so, the report doesn’t cover those who change their behavior, hence we set $S_b(0) = 0$, $I_{1b}(0) = 0, I_{2b}(0) = 0$ and $I_{3b}(0) = 0$. Furthermore, we have no data for the AIDS group, hence, $A(0) = 0.$

The migration rate of people in to South Africa is given by 1,039,749 so that $B = 1,039, 749$. Life expectancy at birth in 2019 for male is estimated at 61.5 and 67.7 for female. We calculate the average of these values as 64.6. As we already know that the natural death rate is the reciprocal of life expectancy, then we have $\mu =\frac{1}{64.6}=0.0155$. The AIDS related death is estimated at 23.4% which means 0.234 so that our disease-induced death rate $\tau = 0.234$. According to Afassinou et al. (2017), it was reported that HIV-1 infected individuals who are not on treatment will develop AIDS within 12 years. Therefore, $\rho _2 = \frac{1}{12}= 0.084$. Since $\rho _2$ is for fast progressors while $\rho _1$ is for slow progressors, we assumed that $\rho _1<\rho _2=0.045$. Other parameter values are given in Table 2.

Definition 3.4

The normalized forward sensitivity analysis index of the basic reproduction number $\mathcal {R}_T$ that depends on the differentiability with respect to a parameter $\alpha$ is defined as

$$\begin{aligned} \displaystyle \Upsilon _{\alpha }^{\mathcal {R}_T}=\displaystyle \frac{\partial \mathcal {R}_T}{\partial \alpha }\times \frac{\alpha }{\mathcal {R}_T}. \end{aligned}$$

(25)

The sensitivity indices of parameters in $\mathcal {R}_T, I_1, I_2$ and $I_3$1 are given in Table . It can be observed from Table 1 that the most sensitive parameter for the increase of the reproduction number is the contact rate $\beta$ and the infection rate $\alpha _3$ for the $I_3$ class . If $\beta$ and $\alpha _3$ are respectively increased by $10\%$, the reproduction number will be increased by 10% and almost 6% respectively. Also the most sensitive parameter for the decrease of the reproduction number is the total abstinence rate $\gamma _1$ and rate of progression to the AIDS class $\rho _2$. If $\gamma _1$ and $\rho _2$ are respectively increased by $10\%$, the reproduction number will be decreased by approximately 10% and 4%, respectively. Increase in $\rho _2$ reduces $\mathcal {R}_T$ because those in AIDS class are assumed weak and unhealthy so causing little damage in disease spread.

For the endemic equilibrium $I_1$, the most sensitive parameter for the increase of $I_1$ class is the recruitment rate B and the infection rate $\alpha _1$. This is because if more people migrate to an infected zone, the infection increases which is the reason behind wide spread of COVID-19 presently claiming lives. For decrease in $I_1$ class, total abstinence $\gamma _3$ and AIDS progression rate $\rho _1$ should be increased.

For the endemic equilibrium $I_2$, the parameters with most negative index is the mortality rate $\mu$. But the mortality rate are not encouraged to be increased so we pick the next most negative parameters which are $\gamma _5$ and $\gamma _1$. Since they are both total abstinence parameters, this shows that total abstinence is inversely proportional to $I_2$, hence they must be increased to reduce the infection rate. More so, B and $\alpha _2$ increase $I_2$ most and must be reduced to ensure reduction in $I_2$ class. $\alpha _3$ was also neglected because its rate of infection and thus, its increase is not encouraged.

Table 1 Sensitivity analysis of parameters in $\mathcal {R}_T,I_1,I_2,I_3$

The same thing goes to $I_3$, the parameter with most negative index is the mortality rate $\mu$. But the mortality rate is not encouraged to be increased so we pick the next most negative parameters which are $\gamma _1$ and $\rho _2$. More so, B and $\alpha _3$ must be reduced to ensure reduction in $I_1$ class. In general, total abstinence parameters $\gamma _{odd}$ are the most sensitive parameters that ensure reduction in the reproduction number and endemic equilibrium. We also note here that a reduction in reproduction number translates to a reduction in endemicity and hence leads to disease eradication. The effects of the most positive and negative parameters on $\mathcal {R}_T$ and endemic equilibrium are shown in the 3D plots.

From Figs. 2, 4, 6 and 8, we can see the effects of the most sensitive parameters with positive indices as they increase $\mathcal {R}_T$, $I_1$, $I_2$ and $I_3$. The higher those parameters, the higher the reproduction number and the endemic equilibrium. Hence, we recommend this parameters are kept as low as possible for HIV/AIDS eradication.

From Figs. 3, 5, 7 and 9, we can see the effects of the most sensitive parameters with negative indices as they decrease $\mathcal {R}_T$, $I_1$, $I_2$ and $I_3$. The higher those parameters, the lower the reproduction number and the endemic equilibrium. Since this parameters are inversely proportional to $\mathcal {R}_T$, $I_1$, $I_2$ and $I_3$ Hence, we recommend this parameters are kept as high as possible for HIV/AIDS eradication.

Fig. 2

Effects of the most sensitive parameters with negative indices on the reproduction number

Fig. 3

Effects of the most sensitive parameters with positive indices on the reproduction number

Fig. 4

Effects of the most sensitive parameters with negative indices on the reproduction number

Fig. 5

Effects of the most sensitive parameters with positive indices on the reproduction number

Fig. 6

Effects of the most sensitive parameters with negative indices on the reproduction number

Fig. 7

Effects of the most sensitive parameters with positive indices on the reproduction number

Fig. 8

Effects of the most sensitive parameters with negative indices on the reproduction number

Fig. 9

Effects of the most sensitive parameters with positive indices on the reproduction number

4 Optimal Control Analysis

The optimal control model is given by:

$$\begin{aligned} \dot{S}(t)&= B - (1 - u_2)(\alpha _1 + \alpha _2 + \alpha _3)\lambda S - (\mu + u_1)S, \end{aligned}$$

(26)

$$\begin{aligned} \dot{S_b}(t)&= u_1S-\mu S_b,\end{aligned}$$

(27)

$$\begin{aligned} \dot{I_1}(t)&= (1 - u_2)\alpha _1\lambda S + \gamma _4I_{1b} - (u_1 + \mu + \rho _1u_3)I_1,\end{aligned}$$

(28)

$$\begin{aligned} \dot{I_{1b}}(t)&= u_1I_1 - (\gamma _4 + \mu )I_{1b},\end{aligned}$$

(29)

$$\begin{aligned} \dot{I_2}(t)&= (1 - u_2)\alpha _2\lambda S + \gamma _6I_{2b} - (\mu + u_1)I_2,\end{aligned}$$

(30)

$$\begin{aligned} \dot{I_{2b}}(t)&= u_1I_2 - (\gamma _6 + \mu )I_{2b},\end{aligned}$$

(31)

$$\begin{aligned} \dot{I_3}(t)&= (1 - u_2)\alpha _3\lambda S + \gamma _8I_{3b} - (u_1 + \mu + \rho _2u_3)I_3,\end{aligned}$$

(32)

$$\begin{aligned} \dot{I_{3b}}(t)&= u_1I_3 - (\gamma _8 + \mu )I_{3b},\end{aligned}$$

(33)

$$\begin{aligned} \dot{A}(t)&= \rho _1I_1u_3 + \rho _2I_2u_3 - (\mu + \tau )A, \end{aligned}$$

(34)

where

$$\begin{aligned} \lambda = \frac{\beta (I_3 + I_{3b}\sigma _1 + \sigma _2I_2 + \sigma _3I_{2b} + \sigma _4I_1 + \sigma _5I_{1b})}{N}. \end{aligned}$$

(35)

The control function $u_1(t), u_1 \in [0, 1]$, connotes government’s intervention aimed at promoting and encouraging change in behavior through total abstinence from all risky activities that leads to HIV-1 contraction or transmission.

The force of infection in the model Eqs. (26)–(34) is reduced by a factor $(1 - u_2(t))$, where $u_2(t) \in [0, 1]$ denotes the fraction of susceptible individuals who maintain a balanced nutritional supplementation aimed at boosting the immune system.

The final control $u_3(t), u_3 \in [0, 1]$, denotes the anti-retroviral treatment intervention on infected individuals. We chose the control functions such that they operate on the time interval $[0, T_f].$ The Pontryagin’s Maximum Principle (Lenhart and Workman 2007) shall be used to determine the conditions under which eradication or reduction of disease is ensured in finite time.

Economically, the effective control of the HIV-1 infection may be too expensive when constant controls are used because it requires treatment at higher levels at all time. We consequently need to consider time dependent controls in order to achieve effective control in finite time. It is worth noting that the disease-free equilibrium will cease to exist when the chosen controls are time dependent (Okosun et al. 2013).

To examine and establish the optimal level of efforts required to curtail the disease burden, we construct an objective functional $\chi (u, u_2, u_3)$, which is to minimize the number of non, slow and fast progressors and the cost of control application, as

$$\begin{aligned} \displaystyle \chi (u_1, u_2, u_3) =\displaystyle \min _{u_1, u_2, u_3}\frac{1}{2}\int _{0}^{T_f}[m_1I_1 + m_2I_2 + m_3I_3 + m_4u_1^2 + m_5u_2^2 + m_6u_3^2]dt, \end{aligned}$$

(36)

subject to the differential quations in (26)–(34), where $T_f$ is the final time, $m_1, m_2, m_3$ are positive weight to balance the factors of the slow progressors individuals, non-progressors individuals and fast progressors infected individuals respectively. Furthermore, $m_4, m_5$ and $m_6$ are positive weight constants for the use of government intervention strategy, nutritional supplementation and antiretroviral treatment efforts respectively which regularize the optimal control. We only included $I_1, I_2$ and $I_3$ because these are the categories of individuals that are worst hit with the infection due to their lack of change in behavior. More so, individuals in these categories are affected by all the three proposed controls which can easily minimize their progression to the AIDS compartment and boost their immune system.

Additionally, the objective functional (36) also contains $m_4u_1^2$, the cost of government intervention aimed at promoting behavior change, $m_5u_2^2$ the cost of ART. We also chose a linear function for the cost of slow-progressors $m_1I_1$, non-progressors $m_2I_2$ and fast-progressors $m_3I_3.$

The weights $m_4, m_5$ and $m_6$ depend on the relative importance of the control efforts in minimizing disease spread as well as the cost of implementing each control efforts per unit time. The effort of government’s intervention to promote behavior change can be through creation of awareness, public health education among others. The cost of treatment could be from cost of medical equipments, drugs, salary of public health workers, follow up of drug management and possible fight against drug-resistance strains. The cost of nutritional supplementation includes cost of eating balanced diet, fruits and vegetables, and so on.

The aim of this analysis is to minimize the number of infected individuals in the slow progression class $I_1(t)$, non-progression class $I_2(t)$ and fast progressor class $I_3(t)$ by decreasing the viral load while minimizing the cost of controls $u_1(t), u_2(t)$ and $u_3(t).$ We seek an optimal control $u_1^*(t), u_2^*(t)$ and $u_3^*(t)$ such that

$$\begin{aligned} \displaystyle \chi (u_1^*(t), u_2^*(t), u_3^*(t)) = \min _{u_1, u_2, u_3 \in \Phi }\displaystyle \chi (u_1, u_2, u_3), \end{aligned}$$

(37)

where

$$\begin{aligned} \Phi = \bigl \{u = (u_1, u_2, u_3) | , 0 \le u_i(t) \le u_{i \text {max}}(t) \le 1~~ \text {for}~~t \in [0, T_f] \rightarrow [0, 1], i = 1,2, 3\bigr \}, \end{aligned}$$

(38)

denotes the control set subject to the system (26)–(34) and its associated initial conditions. It is noteworthy to state that $u_i(t)$ is Lebesgue measurable. This clearly shows that $u_1, u_2$ and $u_3$ lie in [0, 1] while $u_{i \text {max}}$ depends on the quantity of available resources to implement the control strategies. Now, we shall establish the existence of the optimal control and its characterization through the optimality system.

The characterization of the optimal control problem shall be two folds. First will be concerned with the proof of existence of the optimal control problem and second is the establishment of the necessary conditions of the optimal control problem using Pontryagin’s Maximum Principle.

4.1 Existence of an Optimal Control Problem

Here we will discuss, in detail, the existence of the optimal controls $\chi (u_1^*(t), u_2^*(t), u^*_3(t))$ using the approach of (Fleming and Rishel 2012) applied and reproduced in (Ngina et al. 2019).

Theorem 4.1

Suppose the objective functional

$$\begin{aligned} \chi (u_1(t), u_2(t), u_3(t)) = \frac{1}{2}\int _{0}^{T_f}(m_1I_1 + m_2I_2 + m_3I_3 + m_4u_1^2 + m_5u_2^2 + m_6u_3^2)dt, \end{aligned}$$

(39)

is minimized subject to the controls and state variables given in model Eqs. ( 26 )–( 34 ) satisfying the initial conditions

$$\begin{aligned}&S(0) = S_0, S_b(0) = S_{b0}, I_1(0) = I_{10}, I_{1b}(0) = I_{1b0},\nonumber \\&I_2(0)=I_{20}, I_3(0) = I_{30}, I_{3b}(0) = I_{3b0}, A(0) = A_0, \end{aligned}$$

(40)

then there exist optimal controls $~(u_1^*, u_2^*, u_3^* \in \Phi )$ such that

$$\begin{aligned} \chi (u_1^*(t), u_2^*(t), u_3^*(t)) = \min \Bigl \{\chi \bigl [u_1(t), u_2(t), u_3(t)\bigr ] : (u_1{(t)}, u_2{(t)}, u_3{(t)}) \in \Phi \Bigr \}. \end{aligned}$$

(41)

The proof of Theorem 4.1 can be found in Appendix 1.

4.2 Necessary Conditions of the Optimal Control

The Pontryagin’s Maximum Principle shall be adopted in this subsection to achieve our aim.

Theorem 4.2

Given the existence of the optimal control triplet $u_1^*,u_2^*,u_3^*$ and the corresponding solutions

$$\begin{aligned} S,S_b,I_1,I_{1b},I_2,I_{2b},I_{3},I_{3b}, A, \end{aligned}$$

of the optimal control system ( 26 )–( 34 ) that minimizes $\chi (u_1,u_2,u_3)$ over $\Phi$ , then there exist adjoint variables

$$\begin{aligned} \lambda _1, \lambda _2,\lambda _3,\lambda _4,\lambda _5,\lambda _6,\lambda _7,\lambda _8,\lambda _9, \end{aligned}$$

satisfying

$$\begin{aligned} -\frac{d\lambda _i}{dt}=\frac{\partial \mathcal {H}}{\partial \lambda _i}, \end{aligned}$$

where $\mathcal {H}$ is the Hamiltonian and $i=S,S_b,I_1,I_{1b},I_2,I_{2b},I_{3},I_{3b}, A$ , with transversality condition

$$\begin{aligned} \lambda _1(T_f)=\lambda _2(T_f)=\lambda _3(T_f)=\lambda _4(T_f)=\lambda _5(T_f)=\lambda _6(T_f)=\lambda _7(T_f)=\lambda _8(T_f)=\lambda _9(T_f)=0. \end{aligned}$$

Proof

Suppose $u_i^*(t) \in \Phi$, is optimal for the objective functional presented in (36) with fixed final time $T_f$, then there exists a nontrivial absolutely continuous mapping $\lambda (t) : [0, T_f] \rightarrow \mathbb {R}^9$, that is

$$\begin{aligned} \lambda (t) = (\lambda _1(t), \lambda _2(t), \lambda _3(t), \lambda _4(t), \lambda _5(t), \lambda _6(t), \lambda _7(t), \lambda _8(t), \lambda _9(t)). \end{aligned}$$

(42)

Equation (42) is otherwise called adjoint vector which exists subject to the following stated conditions for all $t \in [0, T_f]$.

• (1) The state variables:

  $$\begin{aligned} \frac{dS}{dt}&= \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t)) }{\partial \lambda _1}, \frac{dS_b}{dt} = \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial \lambda _2},\nonumber \\ \frac{dI_1}{dt}&= \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial \lambda _3}, \frac{dI_{1b}}{dt} = \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial \lambda _4},\nonumber \\ \frac{dI_2}{dt}&= \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial \lambda _5}, \frac{dI_{2b}}{dt} = \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial \lambda _6},\nonumber \\ \frac{dI_3}{dt}&= \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial \lambda _7}, \frac{dI_{3b}}{dt} = \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial \lambda _8},\nonumber \\ \frac{dA}{dt}&= \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial \lambda _9}. \end{aligned}$$

  (43)

• (2) The optimality conditions:

  $$\begin{aligned} \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial u_1} = 0, \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial u_2} = 0, \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial u_3} = 0. \end{aligned}$$

• (3) The adjoint equations:

  $$\begin{aligned} \frac{d\lambda _1}{dt}&= - \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial S}, \frac{d\lambda _2}{dt} = - \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial S_b},\\ \frac{d\lambda _3}{dt}&= - \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial I_1}, \frac{d\lambda _4}{dt} = - \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial I_{1b}},\\ \frac{d\lambda _5}{dt}&= - \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial I_2}, \frac{d\lambda _6}{dt} = - \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial I_{2b}},\\ \frac{d\lambda _7}{dt}&= - \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial I_3}, \frac{d\lambda _8}{dt} = - \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial I_{3b}},\\ \frac{d\lambda _9}{dt}&= - \frac{\partial \mathcal {H}(t, u_1^*, u_2^*, u_3^*, \lambda (t))}{\partial A}. \end{aligned}$$

The Lagrangian, in form of augmented Hamiltonian is defined as

$$\begin{aligned}&\mathcal {H}(S, S_b, I_1, I_{1b}, I_2, I_{2b}, I_3, I_{3b}, A, \lambda _1, \lambda _2, \lambda _3, \lambda _4, \lambda _5, \lambda _6, \lambda _7, \lambda _8, \lambda _9, u_1, u_2, u_3)\nonumber \\&\quad = (m_1I_1(t) + m_2I_2(t) + m_3I_3(t) + m_4u_1^2 + m_5u_2^2 + m_6u_3^2)\nonumber \\&\qquad + \lambda _1[B - (1 - u_2)(\alpha _1 + \alpha _2 + \alpha _3)\lambda S - (\mu + u_1)S] + \lambda _2[u_1S - \mu S_b]\nonumber \\&\qquad + \lambda _3[(1 - u_2)\alpha _1\lambda S + \gamma _4I_{1b} - (u_1 + \mu + \rho _1u_3)I_1] + \lambda _4[u_1I_1 - (\gamma _4 + \mu )I_{1b}]\nonumber \\&\qquad + \lambda _5[(1 - u_2)\alpha _2\lambda S + \gamma _6I_{2b} - (\mu + u_1)I_2] + \lambda _6[u_1I_2 - (\gamma _6 + \mu )I_{2b}]\nonumber \\&\qquad + \lambda _7[(1 - u_2)\alpha _3\lambda S + \gamma _8I_{3b} - (u_1 + \mu + \rho _2u_3)I_3] + \lambda _8[u_1I_3 - (\gamma _8 + \mu )I_{3b}]\nonumber \\&\qquad + \lambda _9[\rho _1I_1u_3 + \rho _2I_3u_3 - (\mu + \tau )A] + w_1u_1 + w_2(1 - u_1) + w_3u_2\nonumber \\&\qquad + w_4(1 - u_2) + w_5u_3 + w_6(1 - u_3), \end{aligned}$$

(44)

where $w_i(t) \ge 0, i \in [1, 6]$ are the penalty multipliers which ensure that the control variables $u_1(t), u_2(t)$ and $u_3(t)$ are bounded satisfying:

$$\begin{aligned} w_1u_1&= w_2(1 - u_1) = 0,~~\text {at}~~u_1^*,\\ w_3u_2&= w_4(1 - u_2) = 0,~~\text {at}~~u_2^*,\\ w_5u_3&= w_6(1 - u_3) = 0,~~\text {at}~~u_3^*, \end{aligned}$$

where $u_1^*, u_2^*, u_3^*$ are optimal controls.

From the Pontryagin’s Maximum Principle, we can derive the adjoint variables by partially differentiating Eq. (44) with respect to $S, S_b, I_1, I_2, I_{2b}, I_3, I_{3b}$ and A.

$$\begin{aligned}&\frac{d\lambda _1}{dt} = - \frac{\partial \mathcal {H}}{\partial S} = \frac{\partial }{\partial S}\bigl [\lambda _1\bigl \{-\tilde{K}_1\tilde{K}_2\lambda S - \tilde{K}_3 S\bigr \} \nonumber \\&\quad + \lambda _2u_1S + \lambda _3\tilde{K}_1\alpha _1\lambda S + \lambda _5\tilde{K}_1\alpha _2\lambda S + \lambda _7\tilde{K}_1\alpha _3\lambda S], \end{aligned}$$

(45)

where $\tilde{K}_1 = 1 - u_2, \tilde{K}_2 = \alpha _1 + \alpha _2 + \alpha _3, \tilde{K}_5 = \mu + u_1$,

$$\begin{aligned} \frac{\partial \mathcal {H}}{\partial S} = \frac{\partial }{\partial S}\bigg \{\tilde{K}_1\lambda S[\alpha _1\lambda _3 + \alpha _2\lambda _5 + \alpha _3\lambda _7 - \tilde{K}_2\lambda _1] - \tilde{K}_3S\lambda _1 + \lambda _2u_1S\bigg \}, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial \lambda }{\partial S}&= \frac{\partial }{\partial S}\bigg [\frac{\beta (I_3 + \sigma _1I_{3b} + \sigma _2I_2 + \sigma _3I_{2b} + \sigma _4I_1 + \sigma _5I_{1b})S}{N}\bigg ]=\frac{N\beta \tilde{K}_4-\beta \tilde{K}_4S}{N^2}.\nonumber \\ \frac{\partial \mathcal {H}}{\partial S}&=\frac{\tilde{K}_1N\beta \tilde{K}_4-\beta \tilde{K}_4S}{N^2} (\alpha _1\lambda _3 + \alpha _2\lambda _5 + \alpha _3\lambda _7 - \tilde{K}_2\lambda _1) - \tilde{K}_3\lambda _1 + \lambda _2u_1. \end{aligned}$$

(46)

Multiplying (46) by negative, we have

$$\begin{aligned} -\frac{\partial \mathcal {H}}{\partial S}&= (1 - u_2)\bigg [\frac{N\beta \tilde{K}_4 - \beta \tilde{K}_4S}{N^2}\bigg ]\bigl [(\alpha _1 + \alpha _2 + \alpha _3)\lambda _1 - \alpha _1\lambda _3 - \alpha _2\lambda _5 - \alpha _3\lambda _7\bigr ]\\&\quad + (\mu + u_1)\lambda _1 - \lambda _2u_1, \end{aligned}$$

which implies that

$$\begin{aligned} -\frac{\partial \mathcal {H}}{\partial S}&= (1 - u_2)\beta \bigg [\frac{N\beta \tilde{K}_4 - \beta \tilde{K}_4S}{N^2}\bigg ]\bigl [(\alpha _1 + \alpha _2 + \alpha _3)\lambda _1 - \alpha _1\lambda _3 - \alpha _2\lambda _5 - \alpha _3\lambda _7\bigr ]\\&\quad + (\lambda _1 - \lambda _2)u_1 + \mu \lambda _1. \end{aligned}$$

Finally,

$$\begin{aligned} \frac{d\lambda _1}{dt}=-\frac{\partial \mathcal {H}}{\partial S}=\frac{(1-u_2)\beta \tilde{K}_4(N-S)}{N^2} [\alpha _1(\lambda _1-\lambda _3)+\alpha _2(\lambda _1-\lambda _5)+\alpha _3(\lambda _1-\lambda _7)]+(\lambda _1-\lambda _2)u_1+\mu \lambda , \end{aligned}$$

(47)

where $\tilde{K}_4 = I_3 + \sigma _1I_{3b} + \sigma _2I_2 + \sigma _3I_{2b} + \sigma _4I_1 + \sigma _5I_{1b}.$

Using the same approach, the partial derivative of $\mathcal {H}$ with respect to $S_b,I_1,I_{1b}, I_{2},I_{2b},I_{3},I_{3b},A$ is given by

$$\begin{aligned} \displaystyle \frac{d\lambda _2}{dt} =&\displaystyle -\frac{\partial \mathcal {H}}{\partial S_b} =\displaystyle +\lambda _2\mu ,\nonumber \\ \displaystyle \frac{d\lambda _3}{dt} =&\displaystyle -\frac{\partial \mathcal {H}}{\partial I_1} =\displaystyle -m_1 + \frac{(1 - u_2)\beta S(N\sigma _4 - \tilde{K}_4)}{N^2}\bigl [\alpha _1(\lambda _1 - \lambda _3) + \alpha _2(\lambda _1 - \lambda _5) + \alpha _3(\lambda _1 - \lambda _7)\bigr ]\nonumber \\&+ (\lambda _3 - \lambda _1)u_1 + (\lambda _3 - \lambda _9)\rho _1u_3 + \lambda _3\mu , \nonumber \\ \displaystyle \frac{d\lambda _4}{dt} =&\displaystyle -\frac{\partial \mathcal {H}}{\partial I_{1b}} =\displaystyle \frac{\beta S\tilde{K}_1(N\sigma _5 - \tilde{K}_4)}{N^2}\bigl [\alpha _1(\lambda _1 - \lambda _3) + \alpha _2(\lambda _1 - \lambda _5) + \alpha _3(\lambda _1 - \lambda _7)\bigr ] \nonumber \\&+ \gamma _4(\lambda _4 - \lambda _3) + \lambda _4\mu ,\nonumber \\ \displaystyle \frac{d\lambda _5}{dt} =&\displaystyle -\frac{\partial \mathcal {H}}{\partial I_2} =\displaystyle -m_2 + \frac{(1 - u_2)\beta S(N\sigma _2 - \tilde{K}_4)}{N^2}\bigl [\alpha _1(\lambda _1 - \lambda _3) + \alpha _2(\lambda _1 - \lambda _5) + \alpha _3(\lambda _1 - \lambda _7)\bigr ]\nonumber \\&+ (\lambda _5 - \lambda _6)u_1+\lambda _5\mu ,\nonumber \\ \displaystyle \frac{d\lambda _6}{dt} =&\displaystyle -\frac{\partial \mathcal {H}}{\partial I_{2b}} =\displaystyle \frac{\beta S\tilde{K}_1(N\sigma _3 - \tilde{K}_4)}{N^2}\bigl [\alpha _1(\lambda _1 - \lambda _3) + \alpha _2(\lambda _1 - \lambda _5) + \alpha _3(\lambda _1 - \lambda _7)\bigr ]\nonumber \\&+ \gamma _6(\lambda _6 - \lambda _5) + \lambda _6\mu ,\nonumber \\ \displaystyle \frac{d\lambda _7}{dt} =&\displaystyle -\frac{\partial \mathcal {H}}{\partial I_3} =\displaystyle -m_3 + \frac{(1 - u_2)\beta S(N- \tilde{K}_4)}{N^2}\bigl [\alpha _1(\lambda _1 - \lambda _3) + \alpha _2(\lambda _1 - \lambda _5) + \alpha _3(\lambda _1 - \lambda _7)\bigr ]\nonumber \\&+ (\lambda _7 - \lambda _8)u_1+(\lambda _7-\lambda _9)\rho _2u_3+\lambda _7\mu ,\nonumber \\ \displaystyle \frac{d\lambda _8}{dt} =&\displaystyle -\frac{\partial \mathcal {H}}{\partial I_{3b}} =\displaystyle \frac{\beta S\tilde{K}_1(N\sigma _1 - \tilde{K}_4)}{N^2}\bigl [\alpha _1(\lambda _1 - \lambda _3) + \alpha _2(\lambda _1 - \lambda _5) + \alpha _3(\lambda _1 - \lambda _7)\bigr ] \nonumber \\&+ \gamma _8(\lambda _8 - \lambda _7) + \lambda _8\mu ,\nonumber \\ \displaystyle \frac{d\lambda _9}{dt} =&\displaystyle -\frac{\partial \mathcal {H}}{\partial A} =\displaystyle (\mu +\tau )\lambda _9 , \end{aligned}$$

(48)

where $\lambda _i(T_f)=0,~i=1...9$ are the transversality conditions. $\square$

Theorem 4.3

The optimal controls $(u_1^*, u_2^*, u_3^*)$ which minimize the objective functional defined in ( 39 ) are

$$\begin{aligned} u_1^{*}(t)=&\min \left[ \max \left( 0,\frac{(\lambda _1-\lambda _2)S+(\lambda _3-\lambda _4)I_1+(\lambda _5-\lambda _6)I_2+(\lambda _7-\lambda _8)I_3}{2m_4} \right) ,1 \right] ,~t\in ~[0,T_f], \end{aligned}$$

(49)

$$\begin{aligned} u_2^*(t)=&\min \left[ \max \left( 0,\frac{\alpha _1(\lambda _3-\lambda _1)\lambda S+\alpha _2(\lambda _5-\lambda _1)\lambda S+\alpha _3(\lambda _7-\lambda _1)}{2m_5}\right) ,1 \right] ,~t\in ~[0,T_f],\end{aligned}$$

(50)

$$\begin{aligned} u_3^*(t)=&\min \left[ \max \left( 0,\frac{(\lambda _3-\lambda _9)\rho _1I_1+(\lambda _7-\lambda _9)\rho _2I_3}{2m_6}\right) ,1 \right] , ~t\in ~[0,T_f]. \end{aligned}$$

(51)

Proof

At the optimal control triplet $u_1^*,u_2^*,u_3^*$, the following conditions hold:

$$\begin{aligned} \frac{\partial \mathcal {H}}{\partial u_1}=0, \frac{\partial \mathcal {H}}{\partial u_2}=0,\frac{\partial \mathcal {H}}{\partial u_3}=0. \end{aligned}$$

(52)

Differentiating the Hamiltonian in (44) with respect to control variable $u_1$ on the set $\Lambda :t|0\le u_1(t)\le 1$, we have

$$\begin{aligned} \frac{\partial \mathcal {H}}{\partial u_1}=2m_4u_1-\lambda _1 S+\lambda _2S-\lambda _3I_1+\lambda _4I_1-\lambda _5I_2+\lambda _6I_2-\lambda _7I_3+\lambda _8I_3+w_1-w_2=0. \end{aligned}$$

Putting $u_1=u_1^*$ and solving for $u_1^*$, we have

$$\begin{aligned} u_1^*=\frac{(\lambda _1-\lambda _2)S+(\lambda _3-\lambda _4)I_1+(\lambda _5-\lambda _6)I_2+(\lambda _7-\lambda _8)I_3-w_1+w_2}{2m_4}. \end{aligned}$$

(53)

We need to determine an explicit expression for $u_1^*$ excluding the penalty functions $w_1$ and $w_2$, we come up with three possible cases explained below.

• 1. Let $w_1=w_2=0$ for the set $\left\{ t|0<u_1^*<1\right\}$, in (53), then $u_1^*$ becomes

  $$\begin{aligned} u_1^*=\frac{(\lambda _1-\lambda _2)S+(\lambda _3-\lambda _4)I_1+(\lambda _5-\lambda _6)I_2+(\lambda _7-\lambda _8)I_3}{2m_4}. \end{aligned}$$

• 2. Let $w_1=0$, $w_2\ge 0$ on the set $\left\{ t|u_1^*=1\right\}$, then (53) becomes

  $$\begin{aligned} u_1^*=1=\frac{(\lambda _1-\lambda _2)S+(\lambda _3-\lambda _4)I_1+(\lambda _5-\lambda _6)I_2+(\lambda _7-\lambda _8)I_3+w_2}{2m_4}. \end{aligned}$$

• 3. Lastly, when $w_2=0$, $w_1\ge 0$ on the set $\left\{ 0t|u_1^*=0\right\}$, then (53) becomes

  $$\begin{aligned} u_1^*=0=\frac{(\lambda _1-\lambda _2)S+(\lambda _3-\lambda _4)I_1+(\lambda _5-\lambda _6)I_2+(\lambda _7-\lambda _8)I_3-w_1}{2m_4}, \end{aligned}$$

  which implies

  $$\begin{aligned} \frac{(\lambda _1-\lambda _2)S+(\lambda _3-\lambda _4)I_1+(\lambda _5-\lambda _6)I_2+(\lambda _7-\lambda _8)I_3}{2m_4}\ge 0. \end{aligned}$$

  Therefore, for the control variable $u_1^*$, we have

  $$\begin{aligned} u_1^*(t)=\max \left( 0,\frac{(\lambda _1-\lambda _2)S+(\lambda _3-\lambda _4)I_1+(\lambda _5-\lambda _6)I_2+(\lambda _7-\lambda _8)I_3}{2m_4} \right) . \end{aligned}$$

  Combining all the three cases together, we have

  $$\begin{aligned}&u_1^{*}(t)=\min \left[ \max \left( 0,\frac{(\lambda _1-\lambda _2)S+(\lambda _3-\lambda _4)I_1+(\lambda _5-\lambda _6)I_2+(\lambda _7-\lambda _8)I_3}{2m_4} \right) ,1 \right] ,\\&t\in ~[0,T_f]. \end{aligned}$$

Similarly, to determine an explicit expression for $u_2^*$, we partially differentiate (44) with respect to control variable $u_2$ on the set $\Phi :t|0\le u_2(t)\le 1$. So that we have

$$\begin{aligned} \frac{\partial \mathcal {H}}{\partial u_2}=2m_5u_2+\lambda _1 (\alpha _1+\alpha _2+\alpha _3)\lambda S-\lambda _3\alpha _1\lambda S-\lambda _5\alpha _2\lambda S-\lambda _7\alpha _3\lambda S+w_3-w_4. \end{aligned}$$

Equating this to zero and putting $u_2=u_2^*$, we have

$$\begin{aligned} u_2^*=\frac{\alpha _1(\lambda _3-\lambda _1)\lambda S+\alpha _2(\lambda _5-\lambda _1)\lambda S+\alpha _3(\lambda _7-\lambda _1)\lambda S-w_3+w_4}{2m_5}. \end{aligned}$$

(54)

To determine an explicit expression for $u_2^*$ excluding the penalty functions $w_3$ and $w_4$, we come up with three possible cases as follows:

• 1. Let $w_3=w_4=0$ for the set $\left\{ t|0<u_2^*<1\right\}$ in (54), then $u_2^*$ becomes

  $$\begin{aligned} u_2^*=\frac{\alpha _1(\lambda _3-\lambda _1)\lambda S+\alpha _2(\lambda _5-\lambda _1)\lambda S+\alpha _3(\lambda _7-\lambda _1)\lambda S}{2m_5}. \end{aligned}$$

• 2. Let $w_3=0$, $w_4\ge 0$ on the set $\left\{ t|u_2^*=1\right\}$, then (54) becomes

  $$\begin{aligned} u_2^*=1=\frac{\alpha _1(\lambda _3-\lambda _1)\lambda S+\alpha _2(\lambda _5-\lambda _1)\lambda S+\alpha _3(\lambda _7-\lambda _1)\lambda S+w_4}{2m_5}. \end{aligned}$$

• 3. Lastly, when $w_4=0$, $w_3\ge 0$ on the set $\left\{ t|u_2^*=0\right\}$, then (54) becomes

  $$\begin{aligned} u_2^*=0=\frac{\alpha _1(\lambda _3-\lambda _1)\lambda S+\alpha _2(\lambda _5-\lambda _1)\lambda S+\alpha _3(\lambda _7-\lambda _1)\lambda S-w_3}{2m_5}, \end{aligned}$$

  which implies

  $$\begin{aligned} \frac{\alpha _1(\lambda _3-\lambda _1)\lambda S+\alpha _2(\lambda _5-\lambda _1)\lambda S+\alpha _3(\lambda _7-\lambda _1)\lambda S}{2m_5}\ge 0. \end{aligned}$$

  Therefore, for the control variable $u_2^*$, we have

  $$\begin{aligned} u_2^*=\max \left( 0, \frac{\alpha _1(\lambda _3-\lambda _1)\lambda S+\alpha _2(\lambda _5-\lambda _1)\lambda S+\alpha _3(\lambda _7-\lambda _1)\lambda S}{2m_5}\right) \ge 0. \end{aligned}$$

  Combining all the three cases together, we have

  $$\begin{aligned} u_2^{*}(t)=\left[ \max \left( 0,\frac{\alpha _1(\lambda _3-\lambda _1)\lambda S+\alpha _2(\lambda _5-\lambda _1)\lambda S+\alpha _3(\lambda _7-\lambda _1)\lambda S}{2m_5} \right) ,1 \right] . \end{aligned}$$

Similarly, to determine an explicit expression for $u_3^*$, we partially differentiate (44) with respect to control variable $u_3$ on the set $\Phi :t|0\le u_3(t)\le 1$. So that we have

$$\begin{aligned} u_3^*=\frac{(\lambda _3-\lambda _9)\rho _1I_1+(\lambda _7-\lambda _9)\rho _2I_3-w_5+w_6}{2m_6}. \end{aligned}$$

(55)

To determine an explicit expression for $u_3^*$ excluding the penalty functions $w_5$ and $w_6$, we come up with three possible cases as follows:

• 1. Let $w_5=w_6=0$ for the set $\left\{ t|0<u_3^*<1\right\}$ in (55), then $u_3^*$ becomes

  $$\begin{aligned} u_3^*=\frac{(\lambda _3-\lambda _9)\rho _1I_1+(\lambda _7-\lambda _9)\rho _2I_3}{2m_6}. \end{aligned}$$

• 2. Let $w_5=0$, $w_6\ge 0$ on the set $\left\{ t|u_3^*=1\right\}$, then (55) becomes

  $$\begin{aligned} u_3^*=1=\frac{(\lambda _3-\lambda _9)\rho _1I_1+(\lambda _7-\lambda _9)\rho _2I_3+w_6}{2m_6}. \end{aligned}$$

• 3. Lastly, when $w_6=0$, $w_5\ge 0$ on the set $\left\{ t|u_3^*=0\right\}$, then (55) becomes

  $$\begin{aligned} u_3^*=0=\frac{(\lambda _3-\lambda _9)\rho _1I_1+(\lambda _7-\lambda _9)\rho _2I_3-w_5}{2m_6}, \end{aligned}$$

  which implies

  $$\begin{aligned} \frac{(\lambda _3-\lambda _9)\rho _1I_1+(\lambda _7-\lambda _9)\rho _2I_3}{2m_6}\ge 0. \end{aligned}$$

  Therefore, for the control variable $u_3^*$, we have

  $$\begin{aligned} u_3^*=\max \left( 0, \frac{(\lambda _3-\lambda _9)\rho _1I_1+(\lambda _7-\lambda _9)\rho _2I_3}{2m_6}\right) . \end{aligned}$$

  Combining all the three cases together, we have

  $$\begin{aligned} u_3^{*}(t)=\min \left[ \max \left( 0,\frac{(\lambda _3-\lambda _9)\rho _1I_1+(\lambda _7-\lambda _9)\rho _2I_3}{2m_6}\right) ,1 \right] . \end{aligned}$$

$\square$

4.3 Analysis of the Control Reproduction Number

As usual, using the same approach as in the previous sections, we calculate the control reproduction number as follows. The disease-free equilibrium of (26)–(34) is given by

$$\begin{aligned} \iota ^*=(S^*, S^*_b,I_1^*,I_{1b}^*,I_2^*,I_{2b}^*,I_3^*,I_{3b}^*,A^*)=\left( \frac{B}{\mu +u_1},\frac{u_1B}{\mu (u_1+\mu )},0,0,0,0,0,0,0\right) . \end{aligned}$$

(56)

It can be verified that $\iota ^*$ attracts the same region $\Sigma$ (of model Eqs. (3)–(11)) for Eqs. (26)–(34). By employing the next generation method (Diekmann et al. 1990; Van den Driessche and Watmough 2002), $\mathcal {F}_2$ (the new infection terms) and $\mathcal {V}_2$ (transfer terms) are expressed as

$$\begin{aligned}&\mathcal {F}_2=\left[ \begin{array}{ccccccc} \dfrac{\alpha _1\beta \sigma _4\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _1\beta \sigma _5\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _1\beta \sigma _2\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _1\beta \sigma _3\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _1\beta \mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _1\beta \sigma _1\mu \tilde{K}_1}{\tilde{K}_5}&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ \dfrac{\alpha _2\beta \sigma _4\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _2\beta \sigma _5\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _2\beta \sigma _2\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _2\beta \sigma _3\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _2\beta \mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _2\beta \sigma _1\mu \tilde{K}_1}{\tilde{K}_5}&{}0\\ \\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ \dfrac{\alpha _3\beta \sigma _4\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _3\beta \sigma _5\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _3\beta \sigma _2\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _3\beta \sigma _3\mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _3\beta \mu \tilde{K}_1}{\tilde{K}_5}&{}\dfrac{\alpha _3\beta \mu \sigma _1\tilde{K}_1}{\tilde{K}_5}&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ \end{array} \right] ,\\&\mathcal {V}_2= \left[ \begin{array}{ccccccc} \tilde{K}_3&{}-\gamma _4&{}0&{}0&{}0&{}0&{}0\\ -u_1&{}K_4&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}\tilde{K}_5&{}-\gamma _6&{}0&{}0&{}0\\ 0&{}0&{}-u_1&{}K_6&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}\tilde{K}_7&{}-\gamma _8&{}0\\ 0&{}0&{}0&{}0&{}-u_1&{}K_8&{}0\\ -\rho _1u_3&{}0&{}0&{}0&{}-\rho _2u_3&{}0&{}K_9\\ \end{array} \right] . \end{aligned}$$

Using $\rho$ as the spectral radius (magnitude of the dominate eigenvalue) of the next generation matrix $\mathcal {F}_2\mathcal {V}_2^{-1}$, $\rho (\mathcal {F}_2\mathcal {V}_2^{-1})$ gives the control reproduction number as

$$\begin{aligned} \mathcal {R}_{con}= \frac{\beta \alpha _1\mu (\sigma _4K_4+\sigma _5u_1)\tilde{K}_1}{\tilde{K}_5(\tilde{K}_3K_4-u_1\gamma _4)}+\frac{\beta \alpha _2\mu (\sigma _2K_6+\sigma _3\tilde{K}_5)\tilde{K}_1}{\tilde{K}_5(\tilde{K}_5K_6-u_1\gamma _6)}+\frac{\beta \alpha _3\mu (K_8+u_1\sigma _1)\tilde{K}_1}{\tilde{K}_5(\tilde{K}_7K_8-u_1\gamma _8)}, \end{aligned}$$

(57)

where

$$\begin{aligned} \tilde{K}_1=1-u_2,\tilde{K}_3=u_1+\mu +\rho _1u_3,\tilde{K}_5=\mu +u_1,\tilde{K}_7=u_1+\mu +\rho _2u_3,~ \frac{S^*}{N^*}=\frac{\mu }{\tilde{K}_5}, \gamma _{odd}=u_1. \end{aligned}$$

In the absence of any control strategies, Eq. (57) reduces to Eq. (18).

If the government’s intervention for promoting behavior change $u_1(t)$, is the only considered control strategy then Eq. (57) reduces to

$$\begin{aligned} \mathcal {R}_{con}|_{u_2=u_3=0}=\mathcal {R}_{u_1}= \frac{\beta \alpha _1\mu (\sigma _4K_4+\sigma _5u_1)}{\tilde{K}_5(\bar{K}_3K_4-u_1\gamma _4)}+\frac{\beta \alpha _2\mu (\sigma _2K_6+\sigma _3u_1)}{\tilde{K}_5(\tilde{K}_5K_6-u_1\gamma _6)}+\frac{\beta \alpha _3\mu (K_8+u_1\sigma _1)}{\tilde{K}_5(\bar{K}_7K_8-u_1\gamma _8)}, \end{aligned}$$

(58)

where $\bar{K}_3=\mu +u_1,\bar{K}_7=\mu +u_1$.

If the nutritional supplementation $u_2(t)$, is the only considered control strategy then Eq. (57) reduces to

$$\begin{aligned} \mathcal {R}_{con}|_{u_1=u_3=0}=\mathcal {R}_{u_2}= \frac{\beta \alpha _1\sigma _4\tilde{K}_1}{\mu }+\frac{\beta \alpha _2\sigma _2\tilde{K}_1}{\mu }+\frac{\beta \alpha _3\tilde{K}_1}{\mu }. \end{aligned}$$

(59)

If the only considered control strategy is ART $u_3(t)$, then Eq. (57) reduces to

$$\begin{aligned} \mathcal {R}_{con}|_{u_1=u_2=0}=\mathcal {R}_{u_3}= \frac{\beta \alpha _1\sigma _4}{\hat{K}_3}+\frac{\beta \alpha _2\sigma _2}{\mu }+\frac{\beta \alpha _3}{\hat{K}_7}, \end{aligned}$$

(60)

where $\hat{K}_3=\mu +\rho _1u_3,\hat{K}_7=\mu +\rho _2u_3$.

It is easy to establish that

$$\begin{aligned} \mathcal {R}_{con}\le \mathcal {R}_T, \end{aligned}$$

(61)

for $0\le u_1,u_2,u_3\le 1$ due to possibility of infection reduction in the presence of control interventions. This implies that the behavior change, balanced nutritional supplementation and the ART have positive impact on the reduction of HIV/AIDS in the community.

4.4 Effect of the Control Strategies on the Control Reproduction Number

Here, we shall graphically investigate the effect of the control measures on the transmission of disease using the control reproduction number. The control reproduction number is plotted against the control variables $u_1(t),u_2(t)$ and $u_3(t)$ where unity is considered as perfect and effective impact on disease transmission and zero is considered as unavailability of control interventions.

We shall investigate to what level will behavior change reduces the infection. We shall also determine whether or not eating balanced nutritional supplementation and use of ART will help in reducing HIV/AIDS transmission.

We have

$$\begin{aligned}&\lim _{u_1\rightarrow 1}\mathcal {R}_{con}= \frac{\beta \alpha _1\mu (\sigma _4K_4+\sigma _5)\tilde{K}_1}{{K}_{51}({K}_{31}K_4-\gamma _4)}+\frac{\beta \alpha _2\mu (\sigma _2K_6+\sigma _3)\tilde{K}_1}{{K}_{51}(K_{51}K_6-\gamma _6)}+\frac{\beta \alpha _3\mu (K_8+\sigma _1)\tilde{K}_1}{{K}_{51}(K_{71}K_8-\gamma _8)}, \end{aligned}$$

(62)

$$\begin{aligned} \lim _{u_2\rightarrow 1}\mathcal {R}_{con}= 0, \end{aligned}$$

(63)

$$\begin{aligned}&\lim _{u_3\rightarrow 1}\mathcal {R}_{con}= \frac{\beta \alpha _1\mu (\sigma _4K_4+\sigma _5u_1)\tilde{K}_1}{\tilde{K}_{5}({K}_{32}K_4-\gamma _4u_1)}+\frac{\beta \alpha _2\mu (\sigma _2K_6+\sigma _3u_1)\tilde{K}_1}{\tilde{K}_{5}(\tilde{K}_{5}K_6-\gamma _6u_1)}+\frac{\beta \alpha _3\mu (K_8+\sigma _1u_1)\tilde{K}_1}{\tilde{K}_{5}(K_{72}K_8-u_1\gamma _8)}, \end{aligned}$$

(64)

where

$$\begin{aligned} K_{32}=u_1+\mu +\rho _1,K_{72}=u_1+\mu +\rho _2,K_{51}=1+\mu ,K_{31}=1+\mu +\rho u_3,K_{71}=1+\mu +\rho _2u_3. \end{aligned}$$

Thus, adequate nutritional supplementation $u_2(t)\rightarrow 1$ and an efficient ART $u_3(t)\rightarrow 1$ are very good combination of strategies that can ensure reduction in HIV/AIDS transmission. This is in confirmation with reports (Grobler et al. 2013; Lamb et al. 2012; Jeremiah et al. 2014; Polasa et al. 1984) where they claimed that nutritional deficiency has become a major reason why ART is no more effective in some African countries. ART on empty stomach of starved patients will be null and void while nutritional efficiency and ART combination will guarantee patient’s recovery level and boost immune system. Figures 10, 11, 12, 13, 14, 15 and 16 show the comparison of the control intervention strategies.

Fig. 10

Effects of u₁ on R_con

Fig. 11

Effects of u₂ on R_con

Fig. 12

Effects of Control u₃ on R_con

Fig. 13

Effects of Controls u₁, u₂ and u₁, u₃ on R_con

Fig. 14

Effects of Controls u₁, u₂ and u₁, u₃ on R_con

Fig. 15

Effects of Controls u₂, u₃ and u₁, u₂, u₃ on R_con

Fig. 16

Effects of Controls u₂, u₃ and u₁, u₂, u₃ on R_con

The positive and independent effect of behavior change, nutritional supplementation and ART on the control reproduction number can be noticed in Figures 10, 11 and 12. These control strategies reduced the control reproduction number significantly as expected biologically.

A more positive and combined effects of government’s intervention to promote behavior change and nutritional supplementation, behavior change and ART, and nutritional supplementation and ART on the control reproduction number can be noticed in Figs. 13, 14 and 15. These combined control strategies reduced the control reproduction number more significantly as expected.

The most effective control strategy is the combination of all the three strategies as depicted in Fig. 16.

5 Numerical Solution of the Optimal Control Problem

In this section, we shall solve the optimal control problem to study the effects of promotion of behavior change, $u_1(t)$, nutritional supplementation, $u_2(t)$, and ART, $u_3(t)$ on the transmission dynamics of the disease. We shall carry out the numerical simulation and the results shall be presented graphically. The results shall be investigated and compared in four folds. The first one shall contain the combine effects of controls $u_2(t)$ and $u_3(t)$ while $u_1(t)$ is set to zero. The second shall examine the complementary effects of $u_1(t)$ and $u_2(t)$ while the control $u_3(t)$ is set to zero. The third one shall check the effects of $u_1(t)$ and $u_3(t)$ while the control $u_2(t)$ is set to zero. The fourth and final one shall examine the effects of all controls $u_1(t),u_2(t) ~\text {and}~ u_3(t)$. The fourth-order Runge–Kutta scheme shall be used throughout the analysis. We assumed that the weight functions $m_1=230,m_2=500,m_3=450,m_4=55,m_5=30,m_6=75$ . Other parameter values used are on Table 2.

Table 2 Hypothetical Value of Parameters

In Fig. 17, control $u_2(t)$ for nutritional supplementation and control $u_3(t)$ for ART were used to optimize the objective functional presented in (39). It can be observed in Fig. 17a that intake of nutritional supplementation results in increase in the susceptible class above the level without control measures. The controls $u_2(t)$ and $u_3(t)$ also decrease the levels of infected individuals in the $I_1,I_2$ and $I_3$ classes significantly.

Fig. 17

Simulation of the Model Using controls $u_2$ and $u_3$ only.

In Fig. 18, control $u_1(t)$ for government’s promotion of behavior change and control $u_2(t)$ for nutritional supplementation were used to optimize the objective functional presented in (39). It can be observed in Fig. 18a that intake of nutritional supplementation and change of behavior result in increase in the susceptible class above the level without control measures more than it did in Fig. 17a. The controls $u_1(t)$ and $u_2(t)$ also decrease the levels of infected individuals in the $I_1,I_2$ and $I_3$ classes obviously.

Fig. 18

Simulation of the Model Using controls $u_1$ and $u_2$ only.

In Fig. 19, control $u_1(t)$ and $u_3(t)$ were used to optimize the objective functional in (39). It can be observed in Fig. 19a that change of behavior results in increase in the susceptible class above the level without control measures but not as high as in Figs. 17a and 18a. The controls $u_1(t)$ and $u_3(t)$ also decrease the levels of infected individuals in the $I_1,I_2$ and $I_3$ classes obviously. Though it appears that the effects of $u_1$ and $u_3$ for $I_2(t)$ and $I_3(3)$ classes seem to be of the same level as those in Fig. 18c, d.

Fig. 19

Simulation of the Model Using controls $u_1$ and $u_3$ only.

In Fig. 20, the effects of all the controls in optimizing the objective functional in (39) is of the highest standard. It is second to none among all the aforementioned scenarios. The susceptible population in Fig. 20a increased constantly more than the previous ones. Consequently, the reduction of infections in all the infected classes almost tends to zero which was not the case in the previous scenarios. Hence, we conclude that the combination of all the considered control measures is the best strategy to ensure significant reduction in the disease transmission.

Fig. 20

Simulation of the Model Using all controls $u_1$, $u_2$ and $u_3$

6 Conclusion

This study qualitatively and quantitatively examined an HIV/AIDS-resistant model with behavior change which is absolutely different from existing HIV/AIDS models and provide a better result than the one obtained by Afassinou et al. (2017); Marmor et al. (2006); Okosun et al. (2013) (because their models does not consider the effect of HIV/AIDS resistance and behavior change ) and (Mastahun and Abdurahman 2017) (apart from the fact that the effect of HIV-resistance is missing, the behavior change considered was not as detailed as ours because it only considered one single compartment but ours considered all the compartments except compartment A(t) since behavior change and resistance are of no benefit to this class). Incorporation of resistance to HIV/AIDS and its analysis is one of the novelty of this study. In order to understand the control measures capable of tackling the infectiousness and spread of HIV/AIDS, we considered control $u_1$, which is the government’s intervention in promoting and encouraging behavior change, $u_2$, which represents intake of balanced nutritional supplementation and $u_3$, which connotes antiretroviral therapy (ART). An optimal control problem was developed and analyzed as well as the control reproduction number. It was further explained that if the control reproduction number $\mathcal {R}_{con}<1$, the HIV virus will eventually die out in no time. Hence, the control reproduction number, $\mathcal {R}_{con}$, is an important indication of the level of efforts required to eliminate the virus. We further explicitly explained that $\mathcal {R}_{con}<\mathcal {R}_T,$ for $~0\le u_1,u_2,u_3,\le 1~$ which means increase in the control strategies had a positive impact on the reduction of $\mathcal {R}_T$. In other words, HIV/AIDS can be completely eradicated with full implementation of all the three aforementioned control strategies which is in confirmation with the work of Grobler et al. (2013); Lamb et al. (2012); Jeremiah et al. (2014); Polasa et al. (1984) where they opined that the ART intervention can never be effective in patients with nutritional deficiencies.

Since majority of the citizens of the Southern African countries who are the worst hit of HIV/AIDS are languishing in penury with stark poverty, this study also established that not only the wealthy ones are guarantee of safety from HIV/AIDS due to their capability of ensuring adequate nutritional supplementation or ART treatment. The poor ones can easily change their behavior and practice total abstinence from all HIV/AIDS endemic region and infected objects. This will also go a long way to guarantee their safety even in the midst of poverty.

The sensitivity analysis was also established in order to determine the most sensitive parameters that are responsible for disease transmission with respect to the basic reproduction number and those responsible for disease prevalence with respect to the endemic equilibrium. It was ascertained that the rate of influx of people in to the infected population and total abstinence from all risk practices and endemic areas are some of the most sensitive parameters for disease spread and disease eradication respectively. The graphical representation affirms the analytic results.

The obtained results on the importance of behavior change discussed in the introductory section is also confirmed in our obtained results. Reports on the global AIDS pandemic in Report (2012) for countries like Zambia, Zimbabwe, South Africa, Namibia etc which show great reduction in HIV/AIDS incidence was also confirmed in our analysis as significant reduction of infection rates was recorded according to our numerical simulations. The adverse effect of malnutrition on ART treatment presented by Braitstein et al. (2006); Koethe et al. (2010); Olsen et al. (2014) was also discovered in the numerical simulation of our model. As depicted in Figs. 17, 18, and 20, adequate nutritional supplementation has a great effect in ensuring effective ART usage.

Appendix 1: Proof of Theorem 4.1

Proof

The existence of the control variables can be established with the help of the results obtained in Ngina et al. (2019) via the following five procedures:

• (1) It can be observed that all the stated initial conditions as well as the control variables $u_1, u_2$ and $u_3$ in the control set $\Phi$ are non-negative values and non-empty where $u_i, i = 1, 2, 3$ is a Lebesgue-integrable function on $[0, T_f]$.

• (2) The right hand sides of the model Eqs. (26)–(34) with control variables are bounded by a linear function of the control and state variables whose solutions exist. By definition, each right hand side of system (26)–(34) is continuous and can be expressed as a linear function of $\Phi$, where the coefficients depend on time and state. This translates to the fact that all the control and state variables $u_1, u_2, u_3, S, S_b, I_1, I_{1b}, I_2, I_{2b}, I_3, I_{3b}$ and A are all bounded on $[0, T_f]$. Particularly, the system Eqs. (26)–(34), its control variables and aforementioned initial conditions can be expressed as:

  $$\begin{aligned} \dot{G} = G_1H + G_2(H), \end{aligned}$$

  (65)

  where

  $$\begin{aligned} H = [S,S_b,I_1,I_{1b},I_2,I_{2b},I_3,I_{3b},A]^T, \end{aligned}$$

  (66)

  is the vector of the state variables. Furthermore, $G_1(H)$ and $G_2(H)$ are respectively defined as

  $$\begin{aligned} G_1 = \begin{bmatrix} -\mu &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} -\mu &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} -\mu &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -\mu &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -\mu &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\mu &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\mu &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\mu &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\mu \end{bmatrix}, \end{aligned}$$

  (67)

  and

  $$\begin{aligned} G_2(H) = \begin{bmatrix} B - (1 - u_2)(\alpha _1 + \alpha _2 + \alpha _3)\lambda S - \mu S\\ u_1S\\ (1 - u_2)\alpha _1\lambda S + \gamma _4I_{1b} - (u_1 + \rho _1u_3)I_1\\ u_1I_1 - \gamma _4I_{1b}\\ (1 - u_2)\alpha _2\lambda S + \gamma _6I_{2b} - u_1I_2\\ u_1I_2 - \gamma _6I_{2b}\\ (1 - u_2)\alpha _3\lambda S + \gamma _8I_{3b} - (u_1 + \rho _2u_3)I_3\\ u_1I_3 - \gamma _8I_{3b}\\ \rho _1I_1u_3 + \rho _2I_2u_3 - \tau A \end{bmatrix}. \end{aligned}$$

  (68)

  Let

  $$\begin{aligned} P(H) =G_1H + G_2(H), \end{aligned}$$

  (69)

  and then $G_2(H)$ in (69) satisfies

  $$\begin{aligned} |G_2(H_1) - G_2(H_2)|&\le r_1|S_1(t) - S_2(t)| + r_2|S_{b_1}(t) - S_{b_2}(t)|\\&+ r_3|I_{11}(t) - I_{12}(t)| + r_4|I_{1b_1}(t) - I_{1b_2}|\\&+ r_5|I_{21}(t) - I_{22}(t)| + r_6|I_{2b_1}(t) - I_{2b_2}(t)|\\&+ r_7|I_{31}(t) - I_{32}(t)| + r_8|I_{3b_1}(t) - I_{3b_2}(t)|\\&+ r_9|A_1(t) - A_2(t)|\\&\quad \le r\bigr [|S_1(t) - S_2(t)| + |S_{b_1}(t) - S_{b_2}(t)|\\&+ |I_{11}(t) - I_{12}(t)| + |I_{1b_1}(t) - I_{1b_2}(t)|\\&+ |I_{21}(t) - I_{22}(t)| + |I_{2b_1}(t) - I_{2b_2}(t)|\\&+ ||I_{31}(t) - I_{32}(t)| + |I_{3b_1}(t) - I_{3b_2}(t)|\\&+ |A_1(t) - A_2(t)|], \end{aligned}$$

  where the positive constant $r = \max (r_i, i = 1, 2, 3,..., 9)$ is independent of the state variables. Furthermore, $P(H_1) - P(H_2) \le r|H_1 - H_2|,$ where $r = \sum _{i = 1}^{9}r_i + \Vert M\Vert \le \infty .$ It can be deduced that the function P(H) is uniformly Lipschitz continuous. From the restrictions on the non-negativeness of the state variables and the definition of the control variables $u_1, u_2, u_3$, the solutions of the model Eq. (65) exist.

• (3) The control set $\Phi$ is convex and closed.

  The elements of the control set $\Phi$ in a vector form are given by

  $$\begin{aligned} \Phi = (u_1, u_2, u_3),~~ \text {where}~~0 \le u_1, u_2, u_3 \le 1. \end{aligned}$$

  (70)

  Next is to establish the convexity of $\Phi$ in the following lines.

  Let $v = (v_1, v_2, v_3)$ be another element in $\Phi$, such that $0 \le v_1, v_2, v_3 \le 1.$ Now, we need to establish that

  $$\begin{aligned} z = \lambda u + (1 - \lambda )v,~~~\text {for}~~0 \le \lambda \le 1, \end{aligned}$$

  is also contained in $\Phi$.

  $$\begin{aligned} z&= \lambda (u_1, u_2, u_3) + (1 - \lambda )(v_1, v_2, v_3)\\&= \bigl [\lambda u_1 + (1 - \lambda )v_1, \lambda u_2 + (1 - \lambda )v_2, \lambda u_3 + (1 - \lambda )v_3 \bigr ]\\&= (z_1, z_2, z_3). \end{aligned}$$

  Then, we have the following pairs:

  $$\begin{aligned} z_1&= \lambda u_1 + (1 - \lambda )v_1,~~ \text {which is in the interval} ~[0,1], ~\text {thus}~ 0 \le z_1 \le 1 ,\\ z_2&= \lambda u_2 + (1 - \lambda )v_2,~~\text {which is in the interval} ~[0,1], ~\text {thus}~ 0 \le z_2 \le 1,\\ z_3&= \lambda u_3 + (1 - \lambda )v_3,~~ \text {which is in the interval} ~[0,1], ~\text {thus}~ 0 \le z_3 \le 1. \end{aligned}$$

  Therefore, $z = (z_1, z_2, z_3)$ satisfies the conditions (70) for convexity. Therefore, we conclude that the control set $\Phi$ is bounded and convex thereby satisfying the condition 3 above.

• (4) Next is to establish that the integrand

  $$\begin{aligned} B = \frac{1}{2}\bigl [m_1I_1 + m_2I_2 + m_3I_3 + m_4u_1^2 + m_5u_2^2 + m_6u_3^2\bigr ], \end{aligned}$$

  (71)

  as appeared in the objective functional is convex in $\Phi$ using the Hessian matrix approach. Before that, we have the following definition:

$\square$

Definition 6.1

Let $Q(z_1, z_2, z_3, \cdots , z_n)$ be a function of many variables, the function Q is said to be concave if and only if the Hessian matrix $(H^{es})$

$$\begin{aligned} H^{es}(z) = \left[ \frac{\partial ^2Q}{\partial z_i\partial z_j}\right] \le 0,~~\forall ~~z \ne 0, \end{aligned}$$

and convex if and only if

$$\begin{aligned} H^{es}(z) = \left[ \frac{\partial ^2Q}{\partial z_i\partial z_j}\right] \ge 0,~~\forall ~~z \ne 0. \end{aligned}$$

Let

$$\begin{aligned} B_i = \frac{1}{2}(m_4u_1^2 + m_5u_2^2 + m_6u_3^2),~~where~~B_i \in B, \end{aligned}$$

then the Hessian matrix $H^{es}$ of $B_i$ is composed as

$$\begin{aligned} H^{es} = \begin{bmatrix} \displaystyle \frac{\partial ^2B_i}{\partial u_1^2} &{} \displaystyle \frac{\partial ^2B_i}{\partial u_1\partial u_2} &{} \displaystyle \frac{\partial ^2B_i}{\partial u_1\partial u_3}\\ \displaystyle \frac{\partial ^2B_i}{\partial u_2\partial u_1} &{} \displaystyle \frac{\partial ^2B_i}{\partial u_2^2} &{} \displaystyle \frac{\partial ^2B_i}{\partial u_2\partial u_3}\\ \displaystyle \frac{\partial ^2B_i}{\partial u_3\partial u_1} &{} \displaystyle \frac{\partial ^2B_i}{\partial u_3\partial u_2} &{} \displaystyle \frac{\partial ^2B_i}{\partial u_3^2} \end{bmatrix} = \begin{bmatrix} m_4 &{} 0 &{} 0\\ 0 &{} m_5 &{} 0\\ 0 &{} 0 &{} m_6 \end{bmatrix} \ge 0. \end{aligned}$$

Since the Hessian matrix $H^{es} \ge 0$, then $B_i$ is convex. If $B_i \in B$ is convex on $\Phi$, then B is also convex on $\Phi$ as required.

• (5) There exist $c_1> 0, c_2 > 0$ and $c_3 > 1$ such that B in (71) which is equivalent to the integrand of $\chi (u, t)$ in (36) is bounded by

  $$\begin{aligned} B(t, S, S_b, I_1, I_{1b}, I_2, I_{2b}, I_3, I_{3b}, A, m_4, m_5, m_6) \le c_2 - c_1(|u_1|^2 + |u_2|^2 + |u_3|^2)^{\frac{c_3}{2}}, \end{aligned}$$

  where $c_1, c_2$ and $c_3$ are constants. From the objective function $\chi (u_1(t), u_2{(t)}, u_3{(t)}),$

  $$\begin{aligned} \chi (u_1(t), u_2(t), u_3(t)) = \frac{1}{2}\bigl [m_1I_1 + m_2I_2 + m_3I_3 + m_4 u_1^2 + m_5u_2^2 + m_6u_3^2\bigr ]. \end{aligned}$$

  Then

  $$\begin{aligned} \chi (u_1(t), u_2(t), u_3(t)) \le m_1I_1 + m_2I_2 + m_3I_3 + m_4 u_1^2 + m_5u_2^2 + m_6u_3^2. \end{aligned}$$

  Suppose $m=\max \left\{ m_4,m_5,m_6 \right\}$ , then

  $$\begin{aligned} \chi (u_1, u_2, u_3) \le m_1I_1 + m_2I_2 + m_3I_3 + m(u_1^2 + u_2^2 + u_3^2), \end{aligned}$$

  (72)

  which implies that

  $$\begin{aligned} m_1I_1 + m_2I_2 + m_3I_3 + m_4u_1^2 + m_5u_2^2 + m_6u_3^2 \le c_2 + c_1(|u_1|^2 + |u_2|^2 + |u_3|^2), \end{aligned}$$

  where $c_2$ depends on the upper bound of $I_1, I_2$ and $I_3$ and $c_1 > 0$ since $m_4> 0, m_5> 0, m_6 > 0.$ Hence, Eq. (72) can be re-expressed as

  $$\begin{aligned} \chi (u_1, u_2, u_3) \le c_2 + c_1(u_1, u_2, u_3)^2. \end{aligned}$$

  (73)

  It is obvious from (73) that $c_1> 0, c_2 > 0$ and $c_3= 2 > 1$ there by satisfying the stated condition 5. Since all the aforementioned conditions are satisfied, then there exist optimal control variables $u_1^*, u_2^*$ and $u_3^*$.

$\square$