No CrossRef data available.
Article contents
Contributions to the Theory of Large Cardinals through the Method of Forcing
Published online by Cambridge University Press: 16 September 2021
Abstract
The dissertation under comment is a contribution to the area of Set Theory concerned with the interactions between the method of Forcing and the so-called Large Cardinal axioms.
The dissertation is divided into two thematic blocks. In Block I we analyze the large-cardinal hierarchy between the first supercompact cardinal and Vopěnka’s Principle (Part I). In turn, Block II is devoted to the investigation of some problems arising from Singular Cardinal Combinatorics (Part II and Part III).
We commence Part I by investigating the Identity Crisis phenomenon in the region comprised between the first supercompact cardinal and Vopěnka’s Principle. As a result, we generalize Magidor’s classical theorems [2] to this higher region of the large-cardinal hierarchy. Also, our analysis allows to settle all the questions that were left open in [1]. Finally, we conclude Part I by presenting a general theory of preservation of 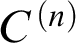 $C^{(n)}$
-extendible cardinals under class forcing iterations. From this analysis we derive several applications. For instance, our arguments are used to show that an extendible cardinal is consistent with “
$C^{(n)}$
-extendible cardinals under class forcing iterations. From this analysis we derive several applications. For instance, our arguments are used to show that an extendible cardinal is consistent with “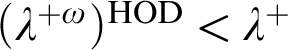 $(\lambda ^{+\omega })^{\mathrm {HOD}}<\lambda ^+$
, for every regular cardinal
$(\lambda ^{+\omega })^{\mathrm {HOD}}<\lambda ^+$
, for every regular cardinal 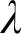 $\lambda $
.” In particular, if Woodin’s HOD Conjecture holds, and therefore it is provable in ZFC + “There exists an extendible cardinal” that above the first extendible cardinal every singular cardinal
$\lambda $
.” In particular, if Woodin’s HOD Conjecture holds, and therefore it is provable in ZFC + “There exists an extendible cardinal” that above the first extendible cardinal every singular cardinal 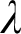 $\lambda $
is singular in HOD and
$\lambda $
is singular in HOD and 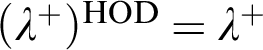 $(\lambda ^+)^{\textrm {{HOD}}}=\lambda ^+$
, there may still be no agreement at all between V and HOD about successors of regular cardinals.
$(\lambda ^+)^{\textrm {{HOD}}}=\lambda ^+$
, there may still be no agreement at all between V and HOD about successors of regular cardinals.
In Part II and Part III we analyse the relationship between the Singular Cardinal Hypothesis (SCH) with other relevant combinatorial principles at the level of successors of singular cardinals. Two of these are the Tree Property and the Reflection of Stationary sets, which are central in Infinite Combinatorics.
Specifically, Part II is devoted to prove the consistency of the Tree Property at both 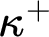 $\kappa ^+$
and
$\kappa ^+$
and 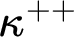 $\kappa ^{++}$
, whenever
$\kappa ^{++}$
, whenever 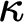 $\kappa $
is a strong limit singular cardinal witnessing an arbitrary failure of the SCH. This generalizes the main result of [3] in two senses: it allows arbitrary cofinalities for
$\kappa $
is a strong limit singular cardinal witnessing an arbitrary failure of the SCH. This generalizes the main result of [3] in two senses: it allows arbitrary cofinalities for 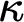 $\kappa $
and arbitrary failures for the SCH.
$\kappa $
and arbitrary failures for the SCH.
In the last part of the dissertation (Part III) we introduce the notion of 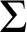 $\Sigma $
-Prikry forcing. This new concept allows an abstract and uniform approach to the theory of Prikry-type forcings and encompasses several classical examples of Prikry-type forcing notions, such as the classical Prikry forcing, the Gitik-Sharon poset, or the Extender Based Prikry forcing, among many others.
$\Sigma $
-Prikry forcing. This new concept allows an abstract and uniform approach to the theory of Prikry-type forcings and encompasses several classical examples of Prikry-type forcing notions, such as the classical Prikry forcing, the Gitik-Sharon poset, or the Extender Based Prikry forcing, among many others.
Our motivation in this part of the dissertation is to prove an iteration theorem at the level of the successor of a singular cardinal. Specifically, we aim for a theorem asserting that every 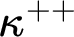 $\kappa ^{++}$
-length iteration with support of size
$\kappa ^{++}$
-length iteration with support of size 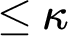 $\leq \kappa $
has the
$\leq \kappa $
has the 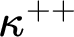 $\kappa ^{++}$
-cc, provided the iterates belong to a relevant class of
$\kappa ^{++}$
-cc, provided the iterates belong to a relevant class of 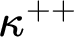 $\kappa ^{++}$
-cc forcings. While there are a myriad of works on this vein for regular cardinals, this contrasts with the dearth of investigations in the parallel context of singular cardinals. Our main contribution is the proof that such a result is available whenever the class of forcings under consideration is the family of
$\kappa ^{++}$
-cc forcings. While there are a myriad of works on this vein for regular cardinals, this contrasts with the dearth of investigations in the parallel context of singular cardinals. Our main contribution is the proof that such a result is available whenever the class of forcings under consideration is the family of 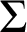 $\Sigma $
-Prikry forcings. Finally, and as an application, we prove that it is consistent—modulo large cardinals—the existence of a strong limit cardinal
$\Sigma $
-Prikry forcings. Finally, and as an application, we prove that it is consistent—modulo large cardinals—the existence of a strong limit cardinal 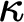 $\kappa $
with countable cofinality such that
$\kappa $
with countable cofinality such that 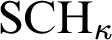 $\mathrm {SCH}_\kappa $
fails and every finite family of stationary subsets of
$\mathrm {SCH}_\kappa $
fails and every finite family of stationary subsets of 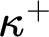 $\kappa ^+$
reflects simultaneously.
$\kappa ^+$
reflects simultaneously.
MSC classification
- Type
- Thesis Abstracts
- Information
- Copyright
- © Association for Symbolic Logic 2021
Footnotes
Supervised by Joan Bagaria.





