Abstract
This paper combines propositional dynamic logic (\({\textsf {PDL}}\)) with propositional inquisitive logic (\(\textsf {InqB}\)). The result of this combination is a logical system \(\textsf {InqPDL}\) that conservatively extends both \({\textsf {PDL}}\) and \(\textsf {InqB}\), and, moreover, allows for an interaction of the question-forming operator from \(\textsf {InqB}\) with the structured modalities from \({\textsf {PDL}}\). We study this system from a semantic as well as a syntactic point of view. These two perspectives are linked via a completeness proof, which also shows that \(\textsf {InqPDL}\) is decidable.


Similar content being viewed by others
Notes
It is common in the literature on inquisitive semantics to abbreviate polar questions by the following definition:
 . We will not employ this convention in the present paper because this use of the question mark would clash with a completely different use of the same symbol in the language of \({\textsf {PDL}}\), where it is used as a test-forming operator.
. We will not employ this convention in the present paper because this use of the question mark would clash with a completely different use of the same symbol in the language of \({\textsf {PDL}}\), where it is used as a test-forming operator.The basic inquisitive logic that we present in this section is sound and complete with respect to the class of all Boolean algebras as well as with respect to the class of complete atomic Boolean algebras. This fact follows from soundness of the axiomatic system presented bellow with respect to arbitrary Boolean algebras and its completeness with respect to complete atomic Boolean algebras. For similar reasons, the inquisitive propositional dynamic logic that we study in the next two sections is sound and complete with respect to the class of all complete Boolean algebras as well as with respect to the class of all complete atomic Boolean algebras. Completeness of the algebras is assumened in this case because it is used in the semantic clauses for \({\textsf {PDL}}\)-operators.
For the connection, see Baltag and Moss (2004), for example.
The symbol \(\cup \) is used in an ambiguous way here. In \(A \cup B\) it stands for the choice operator and in \(R_{A} \cup R_{B}\) it stands for union of sets.
\(R^{*}_A\) is the reflexive transitive closure of the relation \(R_A\). It can be alternatively defined as \(\bigcup _{n \in \omega } R_{A}^{n}\), where \(R_{A}^{n}=\underbrace{R_A \circ \cdots \circ R_A}_{\text {n-times}}\).
Note that we could not proceed in this way without the assumption that \(\alpha \) is
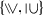 -free.
-free.In this equation, \(\cup \) stands for choice.
In this equation, \(\cup \) stands for union of sets.
See, e.g., Ciardelli (2016), Lemma 3.3.4., p. 86.
We will illustrate this step with an example. Note that due to the axiom InqA9 inquisitive choice is commutative and associative (i.e.
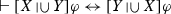 , and similarly with associativity). However, at this point, we cannot use commutativity and associativity of non-inquisitive choice. (That non-inquisitive choice also has these properties will be clear only after we will have proved the disjunctive normal form theorem.) Assume, for example, that \({\mathcal {R}}(Y)=\{B_1, B_2, B_3, B_4 \}\) and
, and similarly with associativity). However, at this point, we cannot use commutativity and associativity of non-inquisitive choice. (That non-inquisitive choice also has these properties will be clear only after we will have proved the disjunctive normal form theorem.) Assume, for example, that \({\mathcal {R}}(Y)=\{B_1, B_2, B_3, B_4 \}\) and 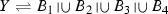 . Then \([Y^*]\psi \) is provably equivalent to the following:
. Then \([Y^*]\psi \) is provably equivalent to the following:-
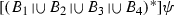
-
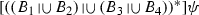 (associativity of
(associativity of  )
) -
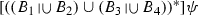 (InqA10)
(InqA10) -
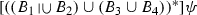 (InqA11)
(InqA11) -
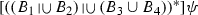 (InqA10)
(InqA10) -
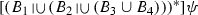 (associativity of
(associativity of 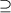 )
) -
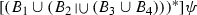 (InqA10)
(InqA10) -
\([(B_1 \cup (B_2 \cup (B_3 \cup B_4)))^{*}] \psi \) (InqA11)
The last formula is identical with \([({\mathcal {R}}(Y)^{\cup })^*]\psi \).
-
The result can be proved also semantically using Theorem 5.
By \(\bigsqcup P\) we mean the least upper bound of elements occurring in the sequence P.
References
Baltag, A., & Moss, L. (2004). Logics for epistemic programs. Synthese, 139, 165–224.
Ciardelli, I., Groenendijk, J., & Roelofsen, F. (2013). Inquisitive semantics: A new notion of meaning. Language and Linguistics Compass, 7, 459–476.
Ciardelli, I., Groenendijk, J., & Roelofsen, F. (2019). Inquisitive semantics. Oxford: Oxford University Press.
Ciardelli, I., & Roelofsen, F. (2011). Inquisitive logic. Journal of Philosophical Logic, 40, 55–94.
Ciardelli, I., & Roelofsen, F. (2015). Inquisitive dynamic epistemic logic. Synthese, 192, 1643–1687.
Ciardelli, I. (2016). Questions in logic. Ph.D. thesis, University of Amsterdam.
Ciardelli, I. (2018). Questions as information types. Synthese, 195, 321–365.
Fischer, M. J., & Ladner, R. E. (1979). Propositional dynamic logic of regular programs. Journal of Computer and System Sciences, 18, 194–211.
Harel, D., Kozen, D., & Tiuryn, J. (2000). Dynamic logic. Cambridge: MIT Press.
Mellema, R. (2019). An inquisitive dynamic epistemic logic with factual change. Master’s thesis. University of Groningen.
Meyer, J.-J. C. (1987). A different approach to deontic logic: Deontic logic viewed as a variant of dynamic logic. Notre Dame Journal of Formal Logic, 29, 109–136.
Pratt, V. (1976). Semantical considerations on Floyd-Hoare logic. In Proceedings of the 17th IEEE symposium on foundations of computer science (pp. 109–121). IEEE Computer Society.
van Gessel, T. (2020). Action models in inquisitive logic. Synthese, 197, 3905–3945.
Yang, F. (2014). On extensions and variants of dependence logic. Ph.D. thesis, University of Helsinki.
Acknowledgements
The work on this paper was supported by the Czech Science Foundation, Grant No. 18-19162Y, the project Non-classical logical models of information dynamics.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Punčochář, V., Sedlár, I. Inquisitive Propositional Dynamic Logic. J of Log Lang and Inf 30, 91–116 (2021). https://doi.org/10.1007/s10849-020-09326-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-020-09326-3




 . We will not employ this convention in the present paper because this use of the question mark would clash with a completely different use of the same symbol in the language of
. We will not employ this convention in the present paper because this use of the question mark would clash with a completely different use of the same symbol in the language of 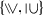 -free.
-free.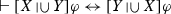 , and similarly with associativity). However, at this point, we cannot use commutativity and associativity of non-inquisitive choice. (That non-inquisitive choice also has these properties will be clear only after we will have proved the disjunctive normal form theorem.) Assume, for example, that
, and similarly with associativity). However, at this point, we cannot use commutativity and associativity of non-inquisitive choice. (That non-inquisitive choice also has these properties will be clear only after we will have proved the disjunctive normal form theorem.) Assume, for example, that 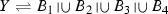 . Then
. Then 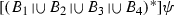
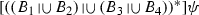 (associativity of
(associativity of  )
)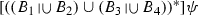 (InqA10)
(InqA10)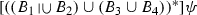 (InqA11)
(InqA11)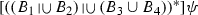 (InqA10)
(InqA10)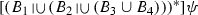 (associativity of
(associativity of 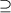 )
)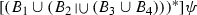 (InqA10)
(InqA10)