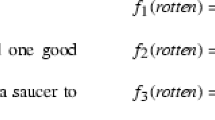Having a look at the Bayes Blind Spot

Abstract

The Bayes Blind Spot of a Bayesian Agent is, by definition, the set of probability measures on a Boolean $\sigma$-algebra that are absolutely continuous with respect to the background probability measure (prior) of a Bayesian Agent on the algebra and which the Bayesian Agent cannot learn by a single conditionalization no matter what (possibly uncertain) evidence he has about the elements in the Boolean $\sigma$-algebra. It is shown that if the Boolean algebra is finite, then the Bayes Blind Spot is a very large set: it has the same cardinality as the set of all probability measures (continuum); it has the same measure as the measure of the set of all probability measures (in the natural measure on the set of all probability measures); and is a “fat” (second Baire category) set in topological sense in the set of all probability measures taken with its natural topology. Features of the Bayes Blind Spot are determined from the perspective of repeated Bayesian learning when the Boolean algebra is finite. Open problems about the Bayes Blind Spot are formulated in probability spaces with infinite Boolean $\sigma$-algebras. The results are discussed from the perspective of Bayesianism.

1 The main claims

The notion of Bayes Blind Spot of a Bayesian Agent was introduced in Gyenis and Rédei (2017): The Bayes Blind Spot is, by definition, the set of probability measures on a Boolean $\sigma$-algebra that are absolutely continuous with respect to the background probability measure (prior) of a Bayesian Agent on the algebra and which the Bayesian Agent cannot learn by a single conditionalization no matter what (possibly uncertain) evidence he has about the elements in the Boolean $\sigma$-algebra. Conditionalization in the most general case involving uncertain evidence is to be understood as conditionalizing using the technique of conditional expectations, of which the usual Bayes rule and Jeffrey conditionalization are special cases (Huttegger 2013; Gyenis and Rédei 2017; Gyenis et al. 2017). The aim of this paper is to determine the properties of the Bayes Blind Spot.

It was shown in Gyenis and Rédei (2017) that the Bayes Blind Spot is a nonempty set in so-called standard probability measure spaces (Definition 4.5 in Petersen 1989). Standard probability spaces include probability spaces with a Boolean algebra having a finite number of elements and also probability spaces on ${\mathrm{I\!R}}^n$ where the probability measure is given by a density function with respect to the Lebesgue measure on ${\mathrm{I\!R}}^n$. These results lead naturally to the question (formulated already in Gyenis and Rédei 2017) of how large the Bayes Blind Spot is. This is a non-trivial problem and there is no unique answer to it in general: The answer depends on both what one takes as the “measure of size” of a set and on the specific properties of the probability measure space. We show in this paper that if the Boolean algebra of the probability space representing the Bayesian Agent’s propositional knowledge has a finite number of elements then the Bayes Blind Spot of this Agent is a very large set, no matter what the prior of the Agent is: The Bayes Blind Spot has the same cardinality as the cardinality of the set of all probability measures on the finite Boolean algebra (continuum); it has the same measure as the measure of the set of all probability measures (in the natural measure on the set of all probability measures); and it is a “fat” (second Baire category) set in topological sense in the set of all probability measures taken with its natural topology.

The large size of the Bayes Blind Spot displays an aspect of the crucial role of priors in Bayesian learning that to our best knowledge has not been noted in the large literature on Bayesian statistical inference so far. The main focus of discussion about priors in Bayesianism is typically about how to chose the prior. Different positions about how to select a prior range from strict subjectivism through objectivism [see Williamson (2010, p. 2) for a brief summary of typical positions]. A large variety of formal methods aiming at selecting priors in Bayesian statistical inference in a disciplined manner also have been developed [see Kaas and Wasserman (1996) for a review]. Our result shows that, irrespective of where the prior comes from, any selected prior is extremely restrictive from the perspective of how many probability measures are in principle accessible for the Bayesian agent as posterior obtained as a result of a single act of conditionalization—if the propositional knowledge of the Bayesian Agent is represented by a finite Boolean algebra. (This will be further discussed in Sect. 8.)

The very large size of the Bayes Blind Spot in the finite case leads naturally to the following questions:

• (a) How much can a finite Bayesian Agent learn as a result of repeated conditionalization?

• (b) How large is the Bayes Blind Spot of a non-finite Bayesian Agent?

Question (a) will be dealt with in Sect. 5. We will see that the answer to it depends very sensitively on how precisely Bayesian repeated learning and the associated Bayes Blind Spot of repeated learning are defined. We will define two types of Bayesian learning dynamics and learning paths, called, respectively, “conservative” and “bold”. These two dynamics differ in whether the Bayesian Agent is ready to give up his prior after each conditionalizing and accept the inferred probability measure as new prior (bold Agent) or not (conservative Agent). We will show that given any fixed, infinite conservative or bold Bayes learning paths of a finite Bayesian Agent, their Bayes Blind Spots, understood as the intersection of all the Bayes Blind Spots along the learning steps, remain a large set (Proposition 5.3).

Given the notions of conservative and bold Bayesian dynamics, one also can define Bayes N-Blind Spots with respect to both conservative and bold Bayes dynamics (Definition 5.4): The Bayes N-Blind Spot is the set of probability measures to which there does not lead any (conservative, respectively bold) Bayesian learning path of length less than or equal to N starting from any evidence (N being a natural number). The corresponding infinite Bayes Blind Spots are the intersection of all the (conservative, respectively bold) Bayes N-Blind Spots ($N=1,2\ldots$). We will see that the infinite conservative Bayes Blind Spot is a very large set if the Boolean algebra is finite. In sharp contrast, the bold Bayes 2-Blind Spot (hence also the bold infinite Bayes Blind Spot) of a Bayesian Agent is empty if the Boolean algebra is finite (Proposition 5.5). Thus, given any probability on a finite Boolean algebra, an Agent having a faithful prior can learn this probability from some specific (possibly uncertain) evidence in only two steps of conditioning—if the Agent discards his prior after the first conditioning and performs the second conditioning using as prior the probability learned in the first step. While this is in principle an attractive feature of Bayesian conditioning, it should be emphasized that the Agent must have access to very specific evidence to be able to infer the given probability in only two steps.

Determining the size of the Bayes Blind Spot of a Bayesian Agent represented by a general probability measure space (question (b) above) seems to be a difficult problem. In Sect. 8 we collect the known results proved on this problem in Gyenis and Rédei (2017). This section formulates some further possible lines of inquiry.

2 Learning by conditionalizing

A Bayesian Agent is an abstract, ideal person having degrees of belief p(C) about (the truths of) propositions C in a set $\mathcal{S}$ forming a Boolean $\sigma$-algebra. The degrees of belief p(C) behave like probabilities: p is an additive map on $\mathcal{S}$ formed by (some) subsets of the set X of elementary propositions. The triplet $(X,\mathcal{S},p)$ is a probability measure space (Billingsley 1995; Rosenthal 2006). For monographic works on Bayesianism we refer to Howson and Urbach (1989), Bovens and Hartmann (2004) and Williamson (2010); for papers discussing basic aspects of Bayesianism, including conditionalization, see Howson and Franklin (1994), Howson (1996, 2014), Hartmann and Sprenger (2010), Easwaran (2011a, b) and Weisberg (2011, 2015); for a discussion of Jeffrey conditionalization, see Diaconis and Zabell (1982) and Huttegger (2015). From now on it is assumed that the Boolean algebra $\mathcal{S}$ has a finite number of elements. (In Sect. 8 we will comment on the situation when $\mathcal{S}$ is infinite.)

A Bayesian Agent is able to perform probabilistic inference on the basis of learning evidence: Suppose the Agent learns that proposition $A\in \mathcal{S}$ is true (but he knows nothing else about other propositions in $\mathcal{S}$). Using his background probability p, if $p(A)\not =0$, the Agent can infer from this information probabilities q(B) of events B other than A by conditionalizing p via A using Bayes’ rule:

$$\begin{aligned} q(B)=\frac{p(B\cap A)}{p(A)} \quad \text{ for } \text{ all } B\in \mathcal{S}\end{aligned}$$

(1)

q is a new probability measure on $\mathcal{S}$; it can be viewed as the probability measure that the Agent has inferred, on the basis of his prior p, from the probability measure $q_{\mathcal{A}}$ that is defined on the four element Boolean subalgebra $\{\emptyset , A, A^{\bot },X\}$ of $\mathcal{S}$ that is generated by A and $A^{\bot }$ and which has the feature that it takes values $q_{\mathcal{A}}(A)=1$ and $q_{\mathcal{A}}(A^{\bot })=0$ on the non-trivial elements of $\mathcal{A}$. The probability measure $q_{\mathcal{A}}$ represents certain evidence (Howson and Franklin 1994, p. 452). Note that q has value 0 on every element B which has p-probability zero. The technical expression of this feature of q is that q is absolutely continuous with respect to p (Billingsley 1995, p. 422).

Remark 2.1

A note on terminology: we used the phrase “conditionalizing p via A using Bayes’ rule” above, rather than just saying “conditionalizing on A”, which would be more standard. We do this because we take the position that conditionalizing is a concept and technique in probability theory that is much more general than the Bayes’ rule (1) [also called “ratio formula” (Rescorla 2015)]: Both the Bayes’ rule and Jeffrey rule (see below) are special cases of conditioning with respect to a $\sigma$-field [see Billingsley (1995, Chapters 33–34) and Gyenis and Rédei (2017) for further discussion of the relation of Bayes’ and Jeffrey rules to the theory of conditionalization via conditional expectation determined by $\sigma$-fields]. We will also say that the “Bayesian Agent learns q on the basis of evidence $q_{\mathcal{A}}$”. This terminology is common in the literature of machine learning/artificial intelligence (Neal 1996; Barber 2012), and it might be slightly confusing because one also says the “Agent learns” the evidence. But the conceptual structure of the situation is clear: The Agent’s “learning” q means the Agent infers q from evidence $q_{\mathcal{A}}$ using conditionalization as inference device.

Suppose that the Agent receives information about A and $A^{\bot }$ that is given by a probability measure $q_{\mathcal{A}}$ which does not have the extreme values 1 and 0 but the values $q_{\mathcal{A}}(A)=r\not = 1$ and $q_{\mathcal{A}}(A^{\bot })=1-r\not =0$. What probability measure can the Agent infer from this evidence on the basis of the background measure p? The standard answer to this question is: If neither p(A) nor $p(A^{\bot })$ is equal to zero, then the Agent can use the Jeffrey conditionalization rule (Jeffrey 1965) to obtain the measure q given by:

$$\begin{aligned} q(B)\doteq \frac{p(B\cap A)}{p(A)}q_{\mathcal{A}}(A)+\frac{p(B\cap A^{\bot })}{p(A^{\bot })}q_{\mathcal{A}}(A^{\bot }) \quad \text{ for } \text{ all } B\in \mathcal{S} \end{aligned}$$

(2)

More generally, if the evidence the Agent has are the probabilities $q_{\mathcal{A}}(A_i)$ of mutually disjoint events $A_i$ ($i=1,2\ldots N$) forming a non-trivial partition in $\mathcal{S}$, which generates the proper, non-trivial Boolean subalgebra $\mathcal{A}$ of $\mathcal{S}$, and if these events have non-zero prior probability $p(A_i)\not =0$ (for all i), then the Agent can infer from this so-called uncertain evidence (Chapter 11 in Jeffrey 1965; Bradley 2005; Weisberg 2009) a probability measure q using the general Jeffrey conditionalizing rule:

$$\begin{aligned} q(B)\doteq \sum _i\frac{p(B\cap A_i)}{p(A_i)}q_{\mathcal{A}}(A_i)\quad \text{ for } \text{ all } B\in \mathcal{S}\end{aligned}$$

(3)

Just like in the case of conditionalization via Bayes’ rule, q obtained this way is absolutely continuous with respect to the prior probability p. To simplify matters, from now on we assume that the prior probability of the Agent is non-zero on every element $\{x\}$ for $x\in X$. In this case, obviously, every probability measure on $\mathcal{S}$ is absolutely continuous with respect to p (see Remark 4.5 for general prior probability).

Remark 2.2

Note that the requirement that the uncertain evidence is given by a probability measure on a proper, non-trivial partition (equivalently: on a proper, non-trivial Boolean subalgebra $\mathcal{S}$) is important: if the evidence were taken to be a probability measure $q'$ on the whole $\mathcal{S}$, then for every element x in X the Jeffrey rule (3) would entail

$$\begin{aligned} q(\{x\})=\sum _i\frac{p(\{x\}\cap A_i)}{p(A_i)}q'(A_i)=\frac{p(\{x\})}{p(\{x\})}q'(\{x\})=q'(\{x\}) \end{aligned}$$

(4)

This equation says that every probability measure can be obtained from itself as evidence via the Jeffrey rule—a triviality. But the philosophically relevant question is whether a Bayesian Agent can learn a probability measure from a “genuine evidence”, i.e. from evidence that contains only partial, incomplete information about the probability to learn. This partial information is contained in the values of the probability on a proper subalgebra of the set of all events/propositions.

As an elementary example for the Jeffrey conditionalization consider die throwing: Let $X_6 = \{x_1,x_2,\ldots ,x_6\}$ represent the possible outcomes of throwing a die, and let $\mathcal{S}_6$ be the Boolean algebra of subsets of $X_6$. Assume that the Agent’s background probability p is given on elements $x\in X_6$ according to Fig. 1 below.

Fig. 1

Example of probabilities in die throwing

Consider the partition

$$\begin{aligned} A_1 = \{x_1, x_2\}\quad A_2=\{x_3,x_4,x_5\} \quad A_3=\{x_6\} \end{aligned}$$

(5)

indicated in Fig. 2. Suppose the Agent receives the information $q_{\mathcal{A}}$, where the probability measure $q_{\mathcal{A}}$ is given on the elements of the partition $A_1,A_2,A_3$ by

$$\begin{aligned} q_{\mathcal{A}}(A_1) = \frac{2}{6}\quad q_{\mathcal{A}}(A_2) = \frac{3}{6} \quad q_{\mathcal{A}}(A_3) = \frac{1}{6} \end{aligned}$$

(6)

Using the Jeffrey conditionalization rule (3), the Agent can infer from evidence $q_{\mathcal{A}}$ the probability measure q indicated in Fig. 2.

Fig. 2

Example of inferring probabilities using Jeffrey conditionalization

3 The Bayes Blind Spot

Consider now the question: Suppose the probability distribution describing the results of throws with a die is q given by Fig. 3 above. Can the Bayesian Agent (having p as his background measure) infer this probability q from some probability measure as evidence by conditionalizing using the Jeffrey rule (3)? If so, we call q Bayes accessible or Bayes learnable.

Fig. 3

Is q Bayes accessible?

The question whether q is Bayes accessible is asking whether there exists a non-trivial partition of the 6 element set $X_6$ and a probability measure $q_{\mathcal{A}}$ defined on elements of this partition such that q can be obtained from $q_{\mathcal{A}}$ in the manner (3). The question is not trivial: there exist 203 different partitions in $\mathcal{S}$ [203 is the $6{\text {th}}$ Bell number (Conway and Guy 1996, pp. 91–93)]. Thus, if one would try to answer the question by “brute force”, one would have to consider all the 203 partitions and, for each partition, write out Eq. (3) for every B to obtain a large number of equations to solve with $q_{\mathcal{A}}(A_i)$ as unknowns to see if the system of equations admits a solution. While doable, this procedure becomes intractable in the general situation when the number of elements in the Boolean algebra is very large. One can however find a simple, compact condition that can be used to decide whether a probability measure can be obtained as a conditional probability via Jeffrey conditionalization:

Suppose we have found a partition $\{A_i\}$ and a $q_{\mathcal{A}}$ for which q can be written in the form (3). If the partition $\{A_i\}$ is non-trivial, then at least one of $A_i$ has more than one element from $X_6$. Suppose $A_i$ has two elements $x_1$ and $x_2$. Then (3) entails

$$\begin{aligned} q(\{x_1\})= & {} \sum _i\frac{p(\{x_1\}\cap A_i)}{p(A_i)}q_{\mathcal{A}}(A_i)=\frac{p(\{x_1\})}{p(A_i)}q_{\mathcal{A}}(A_i) \end{aligned}$$

(7)

$$\begin{aligned} q(\{x_2\})= & {} \sum _i\frac{p(\{x_2\}\cap A_i)}{p(A_i)}q_{\mathcal{A}}(A_i)=\frac{p(\{x_2\})}{p(A_i)}q_{\mathcal{A}}(A_i) \end{aligned}$$

(8)

Equations (7)–(8) entail that a necessary condition for q to be Bayes accessible is that the following condition holds:

$$\begin{aligned} \frac{q(\{x_1\})}{p(\{x_1\})}=\frac{q(\{x_2\})}{p(\{x_2\})} \end{aligned}$$

(9)

One can verify easily that the probability measure q describing the distribution of throws with a die with values indicated in Fig. 3violates condition (9). Consequently, this probability measure is not Bayes accessible: A Bayesian Agent having his background knowledge represented by the probability measure p given in Fig. 3 is not able to learn this q distribution via conditionalizing no matter what (possibly uncertain) evidence he is presented with.

The reasoning leading to the necessary condition (9) for Bayes accessibility generalizes easily from $\mathcal{S}_6$ to an arbitrary finite Boolean algebra. This, in turn leads to a sufficient condition entailing that a probability measure is not Bayes accessible: If for a probability measure q on $\mathcal{S}$ we have

$$\begin{aligned} \frac{q(\{x_i\})}{p(\{x_i\})}\not =\frac{q(\{x_j\})}{p(\{x_j\})} \quad i\not =j; \ 1\le i,j\le n \end{aligned}$$

(10)

then q is not Bayes accessible for the Bayesian Agent having p as his background degree of belief.

The function $\frac{dq}{dp}$ defined by

$$\begin{aligned} X\ni x_i\mapsto \frac{dq}{dp}(x_i)\doteq \frac{q(\{x_i\})}{p(\{x_i\})} \end{aligned}$$

(11)

is known as the Radon–Nikodym derivative (also called the density) of q with respect to p (Billingsley 1995, p. 423). Thus, the content of the sufficient condition (10) can be expressed compactly by saying that q is not Bayes accessible for the Bayesian Agent having background probability p if the Radon–Nikodym derivative $\frac{dq}{dp}$ of q with respect to p is an injective function. We show now that this condition also is necessary, i.e. we will prove

Proposition 3.1

(cf. Gyenis and Rédei 2017) Let $(X,\mathcal{S},p)$ be a probability space with a finite set X having n elements and $\mathcal{S}$ the Boolean algebra of subsets of X. A probability measure q on $\mathcal{S}$ is not Bayes accessible if and only if its Radon–Nikodym derivative $\frac{dq}{dp}$ is an injective function.

Proof

Since we have seen that injectivity of the Radon–Nikodym derivative is sufficient for Bayes inaccessibility, we only have to show that injectivity is also necessary, i.e. that non-injectivity entails Bayes accessibility. Let the range of $\frac{dq}{dp}$ be $\{y_1, \ldots , y_k\}$. If $\frac{dq}{dp}$ is not injective, then the partition

$$\begin{aligned} A_i = \big \{ x\in X:\; \frac{dq}{dp}(x) = y_i \big \}\quad \text { for } i=1\ldots k \end{aligned}$$

is a non-trivial partition of X i.e. there is at least one $A_i$ containing at least two elements. Note that $\frac{dq}{dp}$ is constant on every $A_i$. We define the probability measure r on the Boolean subalgebra generated by the partition $A_i$ by defining the values of r on the blocks of the partition and requiring r to be additive:

$$\begin{aligned} r(A_i) = \frac{q(\{x\})}{p(\{x\})}p(A_i)\quad \quad \text { for any }x\in A_i \end{aligned}$$

Then, for all $x\in X$ there is a unique j such that $x\in A_j$ and thus we have

$$\begin{aligned} \sum _{i}\frac{p\big ( \{x\}\cap A_i \big )}{p(A_i)}r(A_i) = \frac{p(\{x\})}{p(A_j)}r(A_j) = q(\{x\}) \end{aligned}$$

$\square$

As the example of die throwing shows, Bayes inaccessible probability measures can exist. More generally, one can show that given any background probability p on a finite Boolean algebra, there exists a q on that Boolean algebra that is Bayes inaccessible (Gyenis and Rédei 2017). Following the terminology introduced in Gyenis and Rédei (2017) we will call the set of probability measures on $\mathcal{S}$ that are not Bayes accessible for the Bayesian Agent (with respect to the fixed background probability p) the “Bayes Blind Spot” of the Agent. If the p-dependence of the Bayes Blind Spot needs to be made explicit, we say “Bayes p-Blind Spot”.

Remark 3.2

Note that we assumed the background probability p to be faithful, which entails that each probability measure on the Boolean algebra $\mathcal{S}$ is absolutely continuous with respect to p. If p is not faithful, then there exist probability measures on $\mathcal{S}$ that are not absolutely continuous with respect to p, and these are trivially not obtainable as conditional probabilities using p as prior. To exclude these trivially non-Bayes accessible probability measures from the Bayes Blind Spot in case when p is not faithful, we define the p-Bayes Blind Spot for such a general p as the set of those probability measures that are absolutely continuous with respect to p and are not Bayes accessible for the Bayesian Agent (with respect to p). Since the main results of the paper state the large size of the Bayes Blind Spot, defining the Bayes Blind Spot more restrictively strengthens the results presented.

4 Size of the Bayes Blind Spot

How large is the Bayes Blind Spot? There is no unique answer to this question: The size of a set can be gauged using conceptually different “yardsticks”. Given a yardstick, one can compare the size of a set to the sizes of other sets, measured by the same yardstick. There are three standard ways to measure the size of a set (Rudin 1987, p. 170) and thus also the size of the Bayes Blind Spot:

Cardinality:

One can ask what the cardinality of the Bayes Blind Spot is and how its cardinality is related to the cardinality of the set of all probability measures.

Topological size:

One can ask whether the Bayes Blind Spot is a meager (Baire first category) or nonmeager (Baire second category) set in the set of all probability measures with respect to a natural topology.

Measure theoretical size:

One can ask what the size of the Bayes Blind Spot is with respect to a measure on the set of all probability measures.

We show now that the Bayes Blind Spot is a very large set in the sense of all the three measures—cardinality, topological and measure theoretical size.

4.1 Cardinality

The sufficient condition (10) for Bayes inaccessibility makes it clear that if $q'$ is Bayes inaccessible, then for all small enough positive real numbers $\varepsilon$ the probability measures $q_{\varepsilon }$ such that

$$\begin{aligned} |q_{\varepsilon }(\{x\})-q'(\{x\})|\le \varepsilon \quad \text {for all} \ x\in X \end{aligned}$$

(12)

also satisfy (10) and thus are not Bayes accessible. It follows from this that the Bayes Blind Spot has at least continuum cardinality (Gyenis and Rédei 2017). On the other hand, the cardinality of the set of all probability measures on a finite Boolean algebra is at most the continuum: a probability measure is a function from the finite set X having n elements into the unit interval [0, 1]; so the set of all probability measures on X is a subset of the cartesian product $\times _1^n[0,1]$, cardinality of which is the same as the cardinality of [0, 1]. It follows that we have the following

Proposition 4.1

The Bayes Blind Spot of a finite Bayesian Agent has the cardinality of the continuum, and, consequently, for such a Bayesian Agent there exist exactly as many Bayes inaccessible probability measures as the number of all probability measures (in the sense of cardinality), namely a continuum number.

4.2 Topological size—Baire category

Recall that, given a subset E of a topological space T, point x in T is an interior point of E if there is an open set O such that x is belongs to O and O is contained in E. The set of all interior points of E is called the interior of E. A subset E of T is said to be nowhere dense if its closure has empty interior. The sets of the first Baire category in T are those that are countable unions of nowhere dense sets (Rudin 1991, p. 42). Any subset of T that is not of the Baire first category is said to be of the second Baire category. A set E is nowhere dense if and only if its complement $T\setminus E$ contains an open set that is dense in T. Thus a subset of T which is open and dense is of the second Baire category.

Sets of first category are “meager”, whereas sets of second category are regarded as nonmeager (“fat”) in a topological sense. To see why, it is useful to have examples.

Consider the real line ${\mathbb {R}}$ with its usual topology. Any finite set of points on the line is a nowhere dense set. The set ${\mathbb {Q}}$ of rational numbers is a meager set because ${\mathbb {Q}}$ is a countable union of single rational numbers.

Non-countable meager sets also exists: the Cantor set is uncountable, closed, compact and nowhere dense in ${\mathbb {R}}$ (see Steen and Seebach 1978). The Cantor set is large in cardinality (within the set of real numbers), small in the sense of topology and also small measure theoretically: it is a null-set with respect to the Lebesque measure. But a meager set can have large measure: the real line can be decomposed into two disjoint sets, one being of first Baire category, the other having measure zero with respect to the Lebesgue measure (Theorem 1.6 in Oxtoby 1980). Such a set is the fat Cantor set (Steen and Seebach 1978), which is meager but can have arbitrary large measure.

Open dense sets are easy to come up with: obviously ${\mathbb {R}}$ is open and dense in itself. Removing a finite number of points from ${\mathbb {R}}$ one obtains an open dense set. Less obvious example is the complement of the Cantor set: since the Cantor set is closed and nowhere dense, its complement is open and dense.

To assess the topological size of the Bayes Blind Spot in the set $M(\mathcal{S})$ of all probability measures on $\mathcal{S}$, we need to specify a topology on $M(\mathcal{S})$. Topologies can be defined by metrics (distance functions), and this is how one can specify a topology in the set of probability measures. There exist several types of metrics among probability measures that one can consider. The Appendix lists five typical ones that occur in different contexts. It turns out (and this is proved in the Appendix) that they all are equivalent in the sense that they determine the same topology, which we will call the standard uniform topology. The content of this topology can be expressed in different ways, one of which is the formulation in terms of the distance $d_3$ of the Appendix: if the probability measure q is $d_3$-close to the probability measure $q'$ then the supremum of the difference of the expectation values of random variables with respect to q and $q'$ is small among all the random variables whose expectation values with respect to the background probability p are close.

Given the standard uniform topology, the topological size of the Bayes Blind Spot is characterized by the following proposition (proof of which we give in the Appendix):

Proposition 4.2

The Bayes Blind Spot of a finite Bayesian Agent is an open and dense set in the set $M(\mathcal{S})$ of all probability measures equipped with the standard uniform topology on the probability measures.

Corollary 4.3

The complement of the Bayes Blind Spot of a finite Bayesian Agent, the set of Bayes accessible probability measures is a closed, nowhere dense set in the standard uniform topology on the probability measures.

Proposition 4.2 says that the Bayes Blind Spot is a very large, a “fat” set in topological sense, much larger than the set of Bayes accessible states. Viewed from the perspective of topology, there exist much more Bayes inaccessible states than Bayes accessible ones.

Corollary 4.3 entails that the limit of Bayes accessible probability measures is again Bayes accessible. Consequently, a Bayes inaccessible probability measure cannot be approximated with arbitrary precision by Bayes accessible probability measures. Thus one cannot “neutralize” the presence of Bayes inaccessible states by taking the position that the Bayesian Agent can in principle be presented with a series of evidences that can get him arbitrarily close to a Bayes inaccessible probability measure.

Furthermore, the set of Bayes accessible probability measures, being the complement of a dense open set, is not only a closed set but a meager set: a closed set with empty interior. Thus, while there exist an uncountably infinite number of Bayes inaccessible probability measures arbitrary close to every Bayes accessible one, every Bayes inaccessible probability measure has a neighborhood in which there are only Bayes inaccessible probability measures.

The Bayes inaccessible probability measures “dominate” the set of all probability measures completely in a topological sense.

4.3 Measure theoretical size

To assess the measure theoretical size of the Bayes Blind Spot in the set $M(\mathcal{S})$, one has to specify a $\sigma$-algebra in $M(\mathcal{S})$ and a measure over this algebra. The natural algebra and measure is the one arising from the Lebesgue measure in the following way:

We can identify measures in $M(\mathcal{S})$ with functions $f:X\rightarrow [0,1]$ such that $\sum _{x\in X}f(x)=1$. Under this identification each probability measure is identified with a point in $[0,1]^n$ (recall: n is the number of elements in X). Thus $M(\mathcal{S})\subseteq [0,1]^{n}$.

The equation

$$\begin{aligned} X_1 + X_2 + \cdots + X_n = 1\quad (X_i\in {\mathbb {R}}\text { a variable}) \end{aligned}$$

(13)

defines an $n-1$-dimensional hyperplane H in ${\mathbb {R}}^n$; thus $M(\mathcal{S})$ is the simplex which is the intersection of this hyperplane with the unit cube $[0,1]^n$ (see the picture below).

For any finite dimension d the d-dimensional Lebesgue measure $\lambda ^{d}$ is defined on the Borel sets of the d-cube $[0,1]^{d}$. Since $M(\mathcal{S})\subseteq H$ is a subset of an $n-1$ dimensional hyperplane in ${\mathbb {R}}^n$, we have $\lambda ^{n}(M(\mathcal{S})) = 0$. On the other hand with $\lambda ^{n-1}$ being the Lebesgue measure on the Borel sets of $H\cap [0,1]^n$ we have

$$\begin{aligned} \lambda ^{n-1}\big (M(\mathcal{S})\big ) = \lambda ^{n-1}\big (H\cap [0,1]^{n}\big ) > 0 \end{aligned}$$

(14)

The measure

$$\begin{aligned} \mu \equiv \frac{\lambda ^{n-1}}{\lambda ^{n-1}(M(\mathcal{S}))} \end{aligned}$$

(15)

is the normalized area (Lebesgue) measure on $M(\mathcal{S})$; in this measure the whole set $M(\mathcal{S})$ of probability measures has measure equal to 1. The next proposition (proved in the Appendix) states the size of the Bayes Blind Spot in this measure.

Proposition 4.4

The Bayes Blind Spot has $\mu$ measure equal to 1. The set of Bayes accessible states is a $\mu$ measure zero set.

Proposition 4.4 says that the Bayes Blind Spot is a very large set in the set of all probability measures, with respect to the natural (Lebesgue) measure in which the set of all probability measures has non-zero measure.¹ “Very large” means here: as large as possible: having the same size as the size of the set of all probability measures. This entails that the Bayes accessible states form a measure zero set in this measure.

Remark 4.5

Propositions 4.1, 4.2 and 4.4 are proved under the assumption that the background probability measure p is faithful. These propositions remain true however if the faithfulness assumption is dropped: If p is not a faithful probability measure, then it has zero probability on some elements in X. In terms of the geometrical picture of figure (Sect. 4.3) this means that the point in the simplex representing p is on an “edge” E of the simplex. All the probability measures that are absolutely continuous with respect to p, hence all the potentially Bayes p-accessible probability measures, are also on E. This edge can be regarded as the set of all probability measures on the Boolean algebra that is obtained from $\mathcal{S}$ by removing from $\mathcal{S}$ the one-element sets on which p is zero, and the restriction $p'$ of p to this Boolean algebra is faithful. Proposition 4.2 entails then, that the set of Bayes $p'$-accessible probability measures is a nowhere dense set in E in the relative topology on E inherited from $M(\mathcal{S})$. But then this set also is a nowhere dense set in $M(\mathcal{S})$, and its complement, the Bayes $p'$-Blind Spot, contains an open dense set, and is thus a set of Baire second category. It follows that the Bayes p-Blind Spot is a set of second Baire category, irrespective of wether p is faithful or not. Since an open and dense set in a complete metric space has to have uncountable cardinality, the Bayes p-Blind Spot has uncountable cardinality irrespective of wether p is faithful or not. Furthermore, since the edge E lies in a proper linear subspace of the linear space in which $M(\mathcal{S})$ has non-zero $\lambda ^{n-1}$ (Lebesgue) measure, the measure of the set of Bayes $p'$-accessible measures in E also has $\lambda ^{n-1}$ measure zero. It follows that the Bayes p-Blind spot has measure 1 in the measure $\mu$ in which $M(\mathcal{S})$ has measure 1 too—irrespective of whether p is faithful.

5 Bayesian dynamics and the Bayes Blind Spot

5.1 Bayes Blind Spots of Bayes learning paths

Once the Bayesian Agent with background measure p has inferred a probability measure q from evidence $q_{\mathcal{A}}$ using the Jeffrey rule (3), he can do one of two things: He can look for further evidence to check which of the inferred probabilities are correct, and, keeping his background probability p, he can perform a second inference that takes into account the new evidence. This learning move, identified and analyzed briefly in Gyenis and Rédei (2017), gives rise to a dynamic of Bayesian learning, which we call here the conservative Bayes dynamic—conservative because the Agent keeps his background probability while repeating conditionalization on the basis of new evidence. “Correct” means in this context that the inferred probability measure is equal to a specific probability measure $p^*$ that the Agent wishes to learn (for instance because $p^*$ represents objectively given frequencies). The other thing the Agent can do is to transform himself into a different Agent by replacing his background belief p with the inferred probability measure q, and, on the basis of this new background measure, he can infer probability measures from new evidences, based on his new prior. This defines a dynamic of Bayesian learning we call bold Bayes dynamic—bold because the Agent accepts the inferred probability measure as background in spite of the fact that the inferred probability might not be the correct $p^*$ the Agent wants to learn. In this section we analyze the Bayes Blind Spot from the perspective of these two types of dynamics.

The precise definitions of the two dynamics are as follows:

Definition 5.1

Let $(X,\mathcal{S},p)$ be a probability space and $\{\mathcal{A}_n\}_{n\in {\mathrm{I\!N}}}$ be an infinite series of (not necessarily different) Boolean $\sigma$-subalgebras of $\mathcal{S}$, each $\mathcal{A}_n$ generated by a $K_n$-element partition $\mathcal{C}_n=\{A^n_i : i=1,2,\ldots K_n\}$. We call $(X,\mathcal{S},p, \{\mathcal{A}_n\}_{n\in {\mathrm{I\!N}}})$ a Bayesian dynamical system.

• 1. Given a probability measure q in $M(\mathcal{S})$, the sequence of probability measures $\{q^c_n\}_{n\in {\mathrm{I\!N}}}$ in $M(\mathcal{S})$ is called a conservative Bayes learning path from q determined by the Bayesian dynamical system $(X,\mathcal{S},p, \{\mathcal{A}_n\}_{n\in {\mathrm{I\!N}}})$ (the superscript c standing for “conservative”) if $q^c_0=q$, and for all $n>0$ the $q^c_n$ is obtained from $q^c_{n-1}$ via the Jeffrey rule (3) using $\mathcal{C}_n$; i.e. for all $n>0$ we have

  $$\begin{aligned} q^c_n(B)\doteq \sum ^{K_n}_i\frac{p(B\cap A^n_i)}{p(A^n_i)}q^c_{n-1}(A^n_i)\quad \text{ for } \text{ all } B\in \mathcal{S}\end{aligned}$$

  (16)

  where for all i the set $A^n_i$ is an element of the partition $\mathcal{C}_n=\{A^n_i : i=1,2,\ldots K_n\}$.

• 2. Given a sequence $\{r_n\}_{n\in {\mathrm{I\!N}}}$ of probability measures in $M(\mathcal{S})$, the sequence of probability measures $\{q^b_n\}_{n\in {\mathrm{I\!N}}}$ in $M(\mathcal{S})$ is called a bold Bayes learning path determined by the Bayesian dynamical system $(X,\mathcal{S},p, \{\mathcal{A}_n\}_{n\in {\mathrm{I\!N}}})$ (the superscript b standing for “bold”) based on the evidence sequence $\{r_n\}_{n\in {\mathrm{I\!N}}}$ if $q^b_0=p$, and for all $n>0$ the $q^b_n$ is obtained from $q^b_{n-1}$ via the Jeffrey rule (3) using $\mathcal{C}_n$ and evidence $r_n$ with the prior being the probability measure $q^b_{n-1}$ inferred in the preceding step, i.e. if for all $n>0$ we have

  $$\begin{aligned} q^b_n(B)\doteq \sum ^{K_n}_i\frac{q^b_{n-1}(B\cap A^n_i)}{q^b_{n-1}(A^n_i)}r_n(A^j_i)\quad \text{ for } \text{ all } B\in \mathcal{S}\end{aligned}$$

  (17)

  where for all i the set $A^n_i$ is an element of the partition $\mathcal{C}_n=\{A^n_i : i=1,2,\ldots K_n\}$.

To simplify notation, in what follows we use $\{q^{\alpha }_n\}_{n\in {\mathrm{I\!N}}}$ to refer to both conservative ($\alpha =c$) and bold ($\alpha =b$) Bayes learning paths.

The bold Bayesian learning is risky in the following sense: When the Bayesian Agent infers $q^b_1$ from $r_1$ on the basis of his prior p via a Jeffrey conditionalization in the first step of the learning process specified by Eq. (17), he cannot be certain that the inferred probability measure $q^b_1$ is correct in the sense of being equal to $p^*$ because $p^*$ might be in the Bayes p-Blind Spot and we know from the propositions in Sect. 4 that it is “overwhelmingly likely” (as measured in terms of the measure $\mu$ defined by Eq. (15) in which the Bayes accessible measures are measure zero) that $p^*$ is in the Bayes p-Blind Spot hence that $q^b_1$ is not correct; yet, the Agent adopts $q^b_1$ as his new prior, on the basis of which he performs the second inference. The same holds for the second, third, and any subsequent inferences via Jeffrey conditionalization: if $p^*$ happens to be in the Bayes $q^b_{n-1}$-Blind Spot, then $q^b_n$ obtained via (17) will be incorrect. It follows that the risk of adopting a wrong probability measure as prior is present at every step in a bold Bayes learning path. To see whether this risk gets reduced as the Agent moves along a Bayes learning path one has to look at the Bayes Blind Spot of the whole learning path, defined as the intersection of the Bayes Blind Spots the Agent has at every step:

Definition 5.2

Let $\{q^{\alpha }_n\}_{n\in {\mathrm{I\!N}}}$ be Bayes Learning paths ($\alpha =c,b$). The Bayes Blind Spots denoted by $BBS[\{q^{\alpha }_n\}_{n\in {\mathrm{I\!N}}}]$ of these Bayes Learning paths are defined as

$$\begin{aligned} BBS[\{q^{\alpha }_n\}_{n\in {\mathrm{I\!N}}}]\doteq \cap _{n=0}^{\infty } BBS(q^{\alpha }_n) \quad \alpha =c,b \end{aligned}$$

(18)

(Recall that BBS(p) denotes the Bayes p-Blind spot of a probability measure p.)

Since in a conservative Bayes learning path the background measure stays the same, at every step on such a conservative learning path the Bayes Blind Spot remains the same and is identical to the Bayes p-Blind Spot: $BBS[\{q^c_n\}_{n\in {\mathrm{I\!N}}}]=BBS(p)$. Thus we can conclude that moving alone a conservative Bayes Learning path does not reduce the size of the Bayes Blind Spot.

In a bold Bayes Learning Path $\{q^b_n\}_{n\in {\mathrm{I\!N}}}$ the priors entering the Jeffrey formula may change at every step: for any j, at step $j+1$ in a bold Bayes learning path $\{q^b_n\}_{n\in {\mathrm{I\!N}}}$, the probability $q^b_j$ is the Agent’s background measure on the basis of which $q^b_{j+1}$ is inferred. For $j>0$, $q^b_j$ may not be faithful even if $q^b_0=p$ is; however, by Remark 4.5 the Bayes $q^b_{j}$-Blind Spot also is a large set topologically: it contains an open dense set and is therefore of second Baire category. Since in a complete metric space the intersection of a countable number of open and dense sets is open and dense by the Baire category theorem (Oxtoby 1980), and since the set $M(\mathcal{S})$ of all probability measures is a metric space with respect to any of the metrics discussed in Sect. 8.1, it follows that the intersection of all the Bayes $q^b_j$-Blind Spots contains an open dense set and is thus a fat (nonmeager) set in the topological sense. Also by Remark 4.5 the Bayes $q^b_j$-accessible states are measure zero for all j [in the measure defined by (15)]. Thus their (countable) union also has measure zero, and it thus follows that the intersection of all the Bayes $q^b_j$-Blind Spots, i.e. $BBS[\{q^b_n\}_{n\in {\mathrm{I\!N}}}]$, has measure 1. Thus what we have shown is the next proposition:

Proposition 5.3

Given any Bayesian dynamical system $(X,\mathcal{S},p, \{\mathcal{A}_n\}_{n\in {\mathrm{I\!N}}})$ with a finite Boolean algebra $\mathcal{S}$, and given any conservative or bold Bayes Learning Paths $\{q^c_n\}_{n\in {\mathrm{I\!N}}}$ and $\{q^b_n\}_{n\in {\mathrm{I\!N}}}$, the Bayes Blind Spots $BBS[\{q^c_n\}_{n\in {\mathrm{I\!N}}}]$ and $BBS[\{q^b_n\}_{n\in {\mathrm{I\!N}}}]$ of both the conservative and bold Bayes Learning Paths are large sets: in cardinality, in the sense of topology and with respect to the natural measure on the set of all probability measures.

5.2 Bayes N-accessibility and the infinite Bayes Blind Spot

Given the notions of conservative and bold Bayesian dynamics, one also can define Bayes N-accessibility with respect to both conservative and bold learning paths of length N. This in turn makes it possible to define the corresponding Bayes N-Blind Spots and an infinite Bayes Blind spot. In this section we define these notions and investigate their properties.

Definition 5.4

Let $(X,\mathcal{S},p)$ represent a Bayesian Agent having degree of belief represented by p.

• i. We say that the probability measure r on $\mathcal{S}$ is Bayes N-accessible for the Bayesian Agent via a conservative (respectively bold) Bayes learning path if there exists a series of (proper, non-trivial) Boolean subalgebras $\{\mathcal{A}_n\}_{n\in {\mathrm{I\!N}}}$ of $\mathcal{S}$ and a conservative $\{q^c_n\}_{n\in {\mathrm{I\!N}}}$ (respectively bold $\{q^b_n\}_{n\in {\mathrm{I\!N}}}$) Bayes learning path (in the sense of Definition 5.1) such that $r=q^c_{N}$ (respectively $r=q^b_{N}$) for some natural number N.

• ii. The conservative (respectively bold) Bayes (p, N)-Blind Spots denoted by $BBS^c(p,N)$ and $BBS^b(p,N)$ of the Bayesian Agent is the set of probability measures on $\mathcal{S}$ that are absolutely continuous with respect to p and which are not Bayes $N'$-accessible via a conservative (respectively bold) Bayes learning path of length $N'$ smaller than or equal to N. The infinite Bayes Blind Spots $BBS^{\alpha }_{\infty }(p)$ ($\alpha =c,b$) are defined as the intersection:

  $$\begin{aligned} BBS^{\alpha }_{\infty }(p)\equiv \cap _{N\in {\mathrm{I\!N}}} BBS^c(p,N) \quad \alpha = c, b \end{aligned}$$

  (19)

Since in a conservative Bayes learning path the background measure stays the same, at every step on such a conservative learning path the Bayes Blind Spot remains the same and is identical to the Bayes p-Blind Spot. Thus $BBS^c_{\infty }[\{q^c_n\}_{n\in {\mathrm{I\!N}}}]=BBS(p)$—the infinite conservative Bayes Blind Spot is a very large set if the Boolean algebra is finite. The situation is radically different in the case of bold Bayes learning:

Proposition 5.5

Let $(X,\mathcal{S},p)$ be a probability measure space with a finite Boolean algebra $\mathcal{S}$ having at least 3 atoms on each of which p has non-zero values. Then the bold Bayes (p, 2)-Blind Spot is empty. As a consequence, the infinite bold Bayes Blind Spot is also empty: $BBS^b_{\infty }(p)=\emptyset$.

Proposition 5.5 states that, given any prior p of a finite Bayesian Agent, for any probability measure $p^*$ (absolutely continuous with respect to the prior) there exists an ordered pair $(r_1, r_2)$ of two probability measures $r_1,r_2$ as (uncertain) evidence such that $p^*$ can be obtained as a result of only two subsequent Jeffrey conditionalizations using evidences $r_1$ and $r_2$—provided the prior p used in the first conditionalization is replaced by the inferred probability in the second conditionalization that uses evidence $r_2$. We prove Proposition 5.5 in the “Appendix”.

6 The Bayes Blind Spot in infinite probability spaces

The results presented in the previous sections lead to several questions concerning the Bayes Blind Spot in probability measure spaces $(X,\mathcal{S},p)$ with an infinite Boolean $\sigma$-algebra $\mathcal{S}$. In this more general situation the general conditioning rule yielding conditional probabilities with respect to arbitrary sub-$\sigma$-fields $\mathcal{A}$ of $\mathcal{S}$ is given by the concept of $(\mathcal{A},p)$-conditional expectation ${\mathscr {E}}(\cdot |\mathcal{A})$ (Billingsley 1995, p. 445), of which the Jeffrey rule (and hence Bayes’ rule) is just particular cases (Gyenis and Rédei 2017; Gyenis et al. 2017). ${\mathscr {E}}_p(\cdot |\mathcal{A})$ is a linear map (projection) on the set $\mathcal{L}^1(X,\mathcal{S},p)$ of p-integrable real valued random variables defined on X. In complete analogy with the Bayes accessibility relation in Sect. 3, this map ${\mathscr {E}}_p(\cdot |\mathcal{A})$ defines a Bayes accessibility relation in the set of probability measures that are absolutely continuous with respect to p, and the notion of p-Bayes Blind Spot also can be defined exactly as in Sect. 3 [for an explicit definition see also Gyenis and Rédei (2017)]. Determining the size of the Bayes p-Blind Spot of a general probability measure space $(X,\mathcal{S},p)$ is a non-trivial problem, with a number of questions still open. At this point, the following partial results are known in the general case:

One can give an abstract, general characterization of probability spaces with a non-empty Bayes Blind Spot (Gyenis and Rédei 2017). On the basis of that characterization one can show the following:

• There exist probability spaces with an empty Bayes Blind Spot. The only example of such a probability space known to us is the one constructed in Gyenis and Rédei (2017). The set of elementary events X of this probability space is very large: its cardinality |X| has to satisfy $|X|>2^{2^{\aleph _0}}$ (with $\aleph _0$ being the countable cardinality).

• The “usual” (technically speaking: the “standard”, see Definition 4.5 in Petersen 1989) infinite probability spaces that occur in applications can be shown to have a Bayes Blind Spot that has the cardinality of the continuum (Gyenis and Rédei 2017). Such probability spaces include the probability measures on ${\mathrm{I\!R}}^n$ given by a density function with respect to the Lebesgue measure in ${\mathrm{I\!R}}^n$. Work is in progress to determine the topological and measure theoretical size of the Bayes Blind Spot of these standard probability spaces (Gyenis and Rédei 2019).

Since the concept of Bayes learning paths make perfect sense in arbitrary probability spaces if one uses the technique of conditional expectations to conditionalize, one also can ask about the properties of the Bayes Blind Spot $BBS[\{q^{b}_n\}_{n\in {\mathrm{I\!N}}}]$ of bold learning paths $\{q^{b}_n\}_{n\in {\mathrm{I\!N}}}$ in the case of infinite Boolean algebras $\mathcal{S}$. We do not have results in this direction; in particular we do not know whether the “bold part” of Proposition 5.3 remains true in the infinite case. It also is not known whether Proposition 5.5 is true for probability measure spaces with an infinite Boolean $\sigma$-algebra; in particular whether the infinite bold Bayes Blind Spot is empty for probability spaces with an infinite Boolean $\sigma$-algebra. Since the proof of Proposition 5.5 relies heavily on the atomicity of finite Boolean algebras, one may conjecture that the infinite Bayes Blind Spot maybe non-empty for certain large (but not too large—see Proposition 6.5 in Gyenis and Rédei 2017) probability spaces. Of special importance would be to know whether the infinite bold Bayes Blind Spot is empty in case of standard probability measure spaces.

7 Some Bayesian models of learning and the Bayes Blind Spot

“Bayesian learning” is not a unique concept. There exist different understandings of learning and learning scenarios and they have different mathematical models based on probability theory; in particular the mathematical notion of conditioning is used in those models in different ways. In this section we comment on the relation of the concept of Bayesian learning as understood in this paper to two other interpretations of learning in a Bayesian manner: Bayesian parameter estimate and merging of probabilities (opinions). The mathematically explicit and precise description of these scenarios requires a lot of technical definition. Giving those details would go way beyond the framework of this paper; hence we just summarize here the main ideas with minimal notation and only to the extent needed to make some points about the relation of the notion of Bayesian learning used in our paper to these scenarios. We also make brief comments on the phenomenon of non-empty Bayes Blind Spots from the perspective of these other ideas about Bayesian learning.

7.1 Bayesian parameter estimate

A classic Bayesian learning scenario is Bayesian parameter estimate. Suppose a probability measure space $(X,{\mathbb {B}}(X),p_{\theta _0})$ describes some situation probabilistically. One wishes to find out, from some “evidence”, what the objective probability measure $p_{\theta _0}$ is. Not knowing what $p_{\theta _0}$ is, one assumes that there is a parameter set $\Theta$ such that for each $\theta \in \Theta$ there is a probability measure $p_{\theta }$ on ${\mathbb {B}}(X)$ that is a possible description of the phenomenon, and parameter $\theta _0$ is a specific element in this set. Assuming furthermore that the parameter set $\Theta$ has some structure that allows forming a probability measure space $(\Theta ,{\mathbb {B}}(\Theta ), \Pi )$ with $\Pi$ being a probability measure on the Boolean algebra ${\mathbb {B}}(\Theta )$, one interprets $\Pi$ as the prior probability of the Bayesian agent about what the “true” parameter is, i.e. about what the true probability measure on ${\mathbb {B}}(X)$ is. One then assumes that observations are made, which result in an infinite sequence $(x_1,x_2,\ldots , x_n,\ldots )$ of random events from X. For any $p_{\theta }$ ($\theta \in \Theta$) one then forms the infinite product probability measure space

$$\begin{aligned} (X^{\infty },{\mathbb {B}}(X)^{\infty }, p^{\infty }_{\theta })\doteq \times _i^{\infty }(X,{\mathbb {B}}(X),p_{\theta }) \end{aligned}$$

(20)

with $p^{\infty }_{\theta }$ being the product measure on ${\mathbb {B}}(X)^{\infty }$. One regards this infinite probability space as one that describes probabilistically the observations of identically distributed independent random events $(x_1,x_2,\ldots , x_n,\ldots )$. One then forms the product probability measure space

$$\begin{aligned} \big (X^{\infty }\times \Theta ,\ {\mathbb {B}}(X)^{\infty }\otimes {\mathbb {B}}(\Theta ), \ P_{\Pi }\big ) \end{aligned}$$

(21)

where the measure $P_{\Pi }$ is a specific combination of the objective probabilities $p^{\infty }_{\theta }$ and of the subjective prior $\Pi$. One can apply techniques of conditioning via conditional expectation in the large probability space (21) to obtain the following type of result, first obtained by Doob (1949) (also see Miller 2018; Freedman 1963): Conditioning the prior $\Pi$ with respect to the observation of the finite segment $(x_1,x_2,\ldots , x_n)$ of the infinite sequence of observations, the conditioned prior tends to the probability measure which concentrates on the parameter $\theta _0$ as $n\rightarrow \infty$, if the distribution of the elements in the infinite sequence is given by the product measure $p^{\infty }_{\theta _{0}}$. This holds for all parameters $\theta _0$ in a set of parameters having probability 1 with respect to the prior $\Pi$.

The Bayesian interpretation of this result is that if one conditionalizes subjective priors defined on the parameter space on the basis of objective probabilities obtained in independent identically distributed trials, then the conditioned subjective prior will concentrate more and more on the parameter that corresponds to the objective probability. While the technical result described above does lend some support to this interpretation, one should not forget about the constraint on this interpretation entailed by the condition that the tendency of the prior to concentrate more and more on $\theta _0$ does not hold for all $\theta _0$ in $\Theta$: it holds only for parameters in a set of probability 1 with respect to the subjective prior $\Pi$. And, as Belot (2013) argues (and as the discussion of size in Sect. 4 also indicates), a probability 0 set need not be small in some other, relevant senses of size (cardinality, topological size). Thus the subjective prior does constrain what can be learned in a Bayesian parameter estimate, and the constraint can be very significant. The precise content of the constraint depends on the specific properties of the prior $\Pi$ [see Belot (2013) for a detailed analysis and Barron et al. (1999) for further technical results on this dependence]. This limitation is not exactly the same as the limitation of Bayesian learning displayed by large Bayes Blind Spots of a prior but is similar in kind: showing limits of a specific Bayesian model of learning entailed by the need of fixing a specific prior in Bayesian learning.

From the perspective of the relation of Bayesian parameter estimate and the existence of large Bayes Blind Spots in finite probability spaces and the notion of Bayesian learning as understood in our paper the following should be noted:

• 1. The conditioning in Bayesian parameter estimate is carried out on a probability space which is the product of the (infinite product of the) “objective” probability measure space and of the space of parameters (= of probability measures on the Boolean algebra of objective random events). This product space, in which conditioning takes place, is infinite. In our framework the prior is not over the joint space of the parameters and outcomes, but only over the space of outcomes. Learning is understood as taking place within this probability space—this is a standard concept of learning, see Diaconis and Zabell (1982). In harmony with this, the main results on the size of the Bayes Blind Spot in our paper hold for finite spaces only.

• 2. The evidence in Bayesian parameter estimate is an infinite sequence of random events with a specific distribution reflecting the probability to be learned. In our framework the evidence is a sharply defined probability measure on a proper, non-trivial subalgebra of the whole Boolean algebra of random events. It is assumed that this probability is given, i.e. that it is known, and we take Bayesian learning as inference from this given, probabilistically accurate, precise and sharp but (from the perspective of the whole set of random events) partial information. In Bayesian parameter estimate the elements in the sequence $(x_1,x_2,\ldots , x_n,\ldots )$ are not restricted to a proper subset of the set of all elementary random events. In harmony with this, at no point in the process of the Agent’s prior approaching the measure concentrating on the true parameter $\theta _0$ will the Agent know necessarily the precise values of the probabilities $p_{\theta _0}(A)$ on any element A, hence on any subalgebra.

The above points make it clear that the model of Bayesian learning considered in our paper is different from Bayesian parameter estimate. The difference can be illustrated on the die throwing example in Sect. 3. To be learned there is the parameter $\theta _0$, which in this case is the ordered 6-tuple (1 / 16, 2 / 16, 3 / 16, 4 / 16, 5 / 16, 1 / 6) represented by the probability measure q (Fig. 3). In Bayesian parameter estimate one assumes that one has as evidence an infinite series of outcomes of throws with the die to find out the value $\theta _0$. The agent’s prior is then on the set of all probability measures on the algebra generated by the six sides of the die, and then the agent proceeds with the parameter estimate as described above. The learning situation we consider in our paper is that the die has been thrown, possibly only a finite number of times, with q giving the actual frequencies of the results of throws. No further throws are allowed. The Agent is asked to infer q, via conditionalization from some evidence, which in this case is the true distribution of the actual outcomes on a proper subalgebra. Such an inference can be made using conditioning but the result depends on a reference measure (prior) used in the conditioning. This prior is on the algebra generated by the six sides of the die. The question we are asking is whether such an inference can always be successful in the sense of yielding q if the agent can have access to any evidence (so interpreted). And the answer is “no” (due to non-empty Bayes Blind Spots).

This example of die throwing shows that the learning scenario we consider is trivial in the case when the Boolean algebra is trivial. This happens in coin-flipping: here the Boolean algebra has only four elements, hence there are no non-trivial sub-Boolean algebras and thus one cannot learn the distribution (frequency) of heads/tails obtained in a series of flips in a non-trivial manner via conditionalization in this simple, meagre probability space, in the way we define Bayesian learning. To put it differently: The Bayes Blind Spot of the probability space $(X,\mathcal{S},p)$ where X has only two random events, is (vacuously) the set of all probability measures on the four element algebra $\mathcal{S}$.

Yet, the kind of Bayesian learning situation we are considering is not exceptional or artificial. It occurs every time one has the task of inferring probabilities from coarse-grained probabilities. Suppose one has aggregate frequency data of occurrence of a certain property P in a population and one wishes to infer from these numbers the frequency of occurrence of P data in other portions of the population. For instance given car accident frequency data (P) in large counties, one may wish to infer car accident frequency data in other (in particular: smaller) municipalities. One can make such an inference by conditioning, and the result of the inferences might be factually correct in an infinite number of cases: whenever the true distribution is not in the Bayes Blind Spot of the prior chosen. But in such a situation our results apply: no matter what the prior, there will be a lot of probability measures (the ones in the Bayes Blind Spot) to which one cannot infer in such situations, and the true probability might be among these.

As described under 2. above, the kind of learning investigated in this paper differs in two significant ways from learning in a Bayesian parameter estimate: (i) input information is stronger, since the agent receives precise probability values of elements in a proper sub-algebra; and (ii) the success criteria is more demanding since it asks that the target measure be learned exactly and not just approximated as sample sizes increase. Since in both of these Bayesian learning models the selected prior constrains what can be learned, the question arises² what the relation of the two constraints are. Specifically: is it true that (some) elements in the Bayes Blind Spot belong to the set of parameters on which the Agent’s prior does not concentrate in the limit? This is an interesting but difficult question to which we do not know the answer. Part of the difficulty is that in Bayesian parameter estimate the probability spaces are infinite and very little is known about the size of the Bayes Blind Spot in the infinite case (cf. Sect. 6). But clarifying the situation would be interesting because one would like to know whether the constraints imposed by the priors in the two models of Bayesian learning strengthen or compensate each other. This could be a topic for further investigation.

7.2 Merging of probabilities

Another type of result discussed in Bayesianism is merging of opinions (Blackwell and Dubins 1962; Kalai and Lehrer 1994) [also see Ryabko (2011, Theorem 2.2)]: Let $(X,\mathcal{S})$ be a measurable space and p, q be two probability measures on $\mathcal{S}$. A countable set $\{\mathcal{P}_n\}$ of measurable partitions of $\mathcal{S}$ is called an information sequence for $(X,\mathcal{S})$ if

• (i) partition $\mathcal{P}_i$ is finer than partition $\mathcal{P}_j$ for $i>j$;

• (ii) the union of the Boolean algebras $\mathcal{A}_n$ generated by partition $\mathcal{P}_n$ generate $\mathcal{S}$;

• (iii) if $q(A)>0$ for an A in a partition $\mathcal{P}_n$, then $p(A)>0$.

Let $v(q,q')$ denote the total variation distance between probability measures q and $q'$ on $\mathcal{S}$. We say that p merges q in the information sequence $\{\mathcal{P}_n\}$ if

$$\begin{aligned} \lim _{n\rightarrow \infty } v(p(\cdot |A_n),q(\cdot |A_n))=0 \end{aligned}$$

if event $A_n$ is in the partition $\mathcal{P}_n$. Roughly: p merges q in the information sequence if the conditional probabilities of p and q with respect to ever finer information become close in the total variation metric.

The major result on merging probability measures is:

Proposition 7.1

(Theorems 1 and 2 in Kalai and Lehrer 1994) p merges q if and only if q is absolutely continuous with respect to p.

If one interprets p and q as priors of two Bayesian Agents, and one assumes mutual absolute continuity of p and q, then the standard interpretation of this result is that Bayesian agents’ views converge after conditioning:

[...] if the opinions of two individuals, as summarized by p and q, agree only in that $p(D)> 0 \leftrightarrow q(D) > 0$ [mutual absolute continuity of p and q], then they are certain that after a sufficiently large finite number of observations [...] their opinions will become and remain close to each other, where close means that for every event E the probability that one man assigns to E differs by at most $\varepsilon$ from the probability that the other man assigns to it, where $\varepsilon$ does not depend on E. Blackwell and Dubins (1962, p. 885)

One also can regard p as the Agent’s prior (i.e. the Agent’s assumption about what the objective probability is) and q as the objective probability describing some phenomenon. Then even if the merging of p and q is interpreted as “learning q” (an interpretation that needs further supporting arguments), this merging is fully compatible with the presence of non-empty Bayes Blind Spots: If p merges q in some information sequence, then q must be absolutely continuous with respect to p by Proposition 7.1; hence q is given by a density function f with respect to p. If f is injective then q is in the Bayes Blind Spot of p [Proposition 3.1 and Gyenis and Rédei (2017, Lemma 6.3)]. This simply means that after any conditionalization based on p as prior (i.e. after extending q from its restriction to any proper Boolean subalgebra $\mathcal{A}$ to the whole Boolean algebra using the ${\mathscr {E}}_p(\cdot |\mathcal{A})$ conditional expectation) the conditioned probability (i.e. the extension) will not be equal to q—in spite of the conditioned probabilities $p(\cdot |A_n)$ and $q(\cdot |A_n)$ of p and q getting closer to each other asymptotically (merging).

The main results in our paper concern the question of what can be learned in a single act of conditioning. But one can in principle take the position that what matters from the perspective of learning probability distributions via conditioning is whether a probability distribution can be “learned approximately”, i.e. approached with arbitrary precision by repeated conditioning. The results in our paper on the behavior of Bayes Blind Spots from the perspective of some specifications of repeated learning show that what can be approximately learned depends very sensitively on how the repeated learning/conditionalization is specified. There is a natural specification of repeated learning via conditioning according to which every probability q that is absolutely continuous with respect to a prior p can be learned approximately in the sense understood in our paper, i.e. via conditioning based on this prior: Let $\mathcal{A}_n$ be a series of proper Boolean subalgebras of $\mathcal{S}$ such that $\mathcal{A}_i\subset \mathcal{A}_j$ ($i<j$) [such a series is called a “filtration” (Billingsley 1995, p. 458)] and assume that the union $\cup ^{\infty }_n\mathcal{A}_n$ generates $\mathcal{S}$. Let f be the density of q with respect to p. Then the upward martingale theorem (Theorem 35.6 in Billingsley 1995) says

$$\begin{aligned} f=\lim _n {\mathscr {E}}_p(f\mid \mathcal{A}_n) \end{aligned}$$

(22)

(the limit pointwise p-a.e.). This means that the probability q can be obtained as the limit of conditioning with respect to the conditional expectation ${\mathscr {E}}_p(\cdot \mid \mathcal{A}_n)$ determined by p and the larger and larger subalgebras $\mathcal{A}_n$. But the existence of non-empty Bayes Blind Spots is also compatible with asymptotic Bayesian learning via conditionalization in this sense in an infinite probability space: if q is in the Bayes Blind Spot of p, then

$$\begin{aligned} f\not ={\mathscr {E}}(f\mid \mathcal{A}_i)) \quad \text{ for } \text{ any } i \text{ such } \text{ that } \mathcal{A}_i\subset \mathcal{S}\end{aligned}$$

(23)

(where the inequality is on a non-p-measure zero set). That is to say, at any step while going to the infinite limit we do not obtain (hence, strictly speaking have not learned) q—if at that stage the conditionalization is with respect to a proper subalgebra of $\mathcal{S}$.

In a finite algebra any filtration generating $\mathcal{S}$ must include the whole set X as the last element; so the martingale equation holds trivially in this case. Accordingly, q cannot be approached in the way (22) if all the elements in the filtration are proper subalgebras of $\mathcal{S}$. This lies at the heart of the large size of the Bayes Blind Spot in finite probability spaces.

8 Concluding remarks

The results presented in the previous section contribute to a better understanding of the role of prior probability in Bayesian learning; more generally of the role of prior probability in any application of probability theory where conditionalization is used.

One lesson of the presented results is that the limits of what can be learned in a single probabilistic inference on the basis of a prior are extremely restrictive in case of a probability theory with a finite set of random events. It should be noted that from the perspective of validity of the results presented in this paper it makes no difference whether the probability measures that are Bayes inaccessible for a Bayesian Agent with a specific prior p are viewed as objectively given or whether they are interpreted as representing subjective degrees of belief: If both the prior probability measure p and the probability measures in the Bayes p-Blind Spot BBS(p) are viewed as representing objective state of affairs (for example frequencies, or some sort of ratios), then the Bayes inaccessibility of the probability measures in BBS(p) presents difficulty for the statistical inference based on p because the objective state of affairs represented by probabilities in BBS(p) are simply not inferable from any incomplete evidence on the basis of p.

In particular this poses a problem for objective Bayesianism, which intends to avoid the arbitrary subjectivism in probabilistic inference; furthermore, the larger the size of BBS(p) the more serious the problem is because less is inferable then via conditionalizing. Thus the large size of the Bayes Blind Spot can be taken as strengthening the arguments against (Bayes or Jeffrey) conditionalization in Williamson’s version of objective Bayesianism (Williamson 2010). If the probability measures are all interpreted subjectively as degrees of belief, then the results on the size of Bayes p-Blind spot and its behavior under repeated inferences contribute to a better understanding of the nature and limits of Bayesian learning dynamic. In particular the fact that (in the finite case) the Bayes p-Blind spot is very large for any prior p whatsoever displays a difficulty that is not related to the arbitrariness of the subjective prior: the difficulty is not that an Agent possibly selects a prior that is biased in a particular way which might distort the posterior probabilities in an unacceptable manner. The problem is that any prior of the Agent prohibits him to obtain an enormously large set of probabilities via conditioning. And this fact is rooted deeply in the concept of (Bayes/Jeffrey) conditionalization; it is a structural, inherent feature of Bayesianism that cannot be “cured” by restricting priors on the basis of some arguments of plausibility or rationality.

One can try to weaken the significance of the large size of Bayes Blind Spot. One way of doing this is to say that not all probability measures on the Boolean algebra are epistemologically relevant, and as a consequence, not all probability measures in the Bayes Blind Spot might be epistemically relevant either. The inaccessibility for the Agent of those irrelevant measures is thus not troubling. For instance, one might say that in a specific context all the epistemologically relevant probability measures are such that they take on values that are rational numbers (e.g. because they represent relative frequencies in finite ensembles). More generally, given some condition of epistemic relevance that restricts the set of all probabilities on a Boolean algebra to a subset $\mathcal{R}$, one could try to determine the size of the intersection of $\mathcal{R}$ and of the Bayes Blind Spot. And this set might be small. It seems plausible that in specific applications of probability theory such restricting epistemic relevance conditions arise naturally. Another way of curtailing the significance of the large size of the Bayes Blind Spot would be to say that the notions of size used in this paper (cardinality, topological size, size in the natural measure) are arbitrary from an epistemological perspective. To articulate this line or reasoning would require the specification of an “epistemologically relevant size”. It’s not clear how one could do this in the abstract; at any rate we do not have any suggestion for such a “size”. But of the three sizes used in our paper to assess the size of the Bayes Blind Spot the topological one does have a clear epistemological interpretation: it is based on closeness of probability measures as this closeness is measured in any of the standard metrics in the set of all probability measures. So the topological largeness of the Bayes Blind Spot has a clear epistemological significance.

Another lesson one can draw from the results is that, in a specific sense, repeated learning via Bayesian/Jeffrey conditionalization modeled by either a conservative or bold Bayes learning path does not mitigate the heavy constraint represented by large Bayes Blind Spots on what can be learned in a Bayesian manner in a finite context: Given any starting prior and given any infinite series of (certain or uncertain) evidences, the set of probability measures learnable via an arbitrary long series of conditionalizations based on this given set of evidence is a very meager set—just as meager as the set that can be learned in a single act of conditioning. Note that this is not in contradiction with the phenomenon known as “washing out of priors”. The relation of washing out of priors [understood in terms of Doob’s upward martingale theorem (Earman 1992, Chapter 6, Sect. 4)] to the inaccessibility of certain probability measures via a possibly infinite series of conditionalization was clarified in Gyenis and Rédei (2017) (see especially Sect. 7 therein).

From the perspective of the power of Bayesian learning a positive result is however Proposition 5.5: This proposition says that given any non-trivial prior, any probability measure $p^*$ (absolutely continuous with respect to the prior) can be learned in not more than two bold steps of (Jeffrey) conditioning on the basis of suitable evidence (if the Boolean algebra is finite). In order not to overestimate this positive feature of bold Bayesian learning one should however keep in mind the following: A look at the proof of Proposition 5.5 makes it clear that the two pieces of evidence $r_1$ and $r_2$ on which the inferences leading to $p^*$ are based have to be very specific: The two sub-Boolean algebras of $\mathcal{S}$ on which $r_1$ and $r_2$ are defined must be perfectly fine-tuned in the sense that they have to generate the whole $\mathcal{S}$. In other words: values of $p^*$ must be revealed on each atom of $\mathcal{S}$ during the two steps of inferences. Thus it pays off to be bold in Bayesian learning indeed—but only if the Agent is confident that he has access to evidence rich enough to yield information about all the values of the probability measure to be learned. This is in harmony with the fact that Bayesian learning understood as statistical inference via conditionalization is an ampliative inference, not a deductive one. This feature Bayesian inference also is reflected by the non-axiomatizability of certain modal logics that are defined semantically in terms of the Bayes accessibility relation (Brown et al. 2018).

Appendix

1.1 Metrics and topology in the set of probability measures on a finite Boolean algebra

Definition 8.1

For $q,r\in M(\mathcal{S})$ we define the following metrics. Chebysev distance:

$$\begin{aligned} d_0(q,r) = \displaystyle \max _{x\in X}\left| q(\{x\})-r(\{x\}) \right| \end{aligned}$$

(24)

Total variation distance I:

$$\begin{aligned} d_1(q,r) = \displaystyle \frac{1}{2}\sum _{x\in X}\left| q(\{x\})-r(\{x\}) \right| \end{aligned}$$

(25)

Total variation distance II:

$$\begin{aligned} d_2(q,r)= & {} \displaystyle \sup \left\{ \left| \sum _{x\in X}f(x)q(\{x\}) - \sum _{x\in X}f(x)r(\{x\})\right| :\; f = \chi _E,\; E\in \mathcal{S}\right\} \\= & {} \displaystyle \max _{E\in \mathcal{S}}\left| q(E)-r(E)\right| \end{aligned}$$

$\Vert \cdot \Vert _1$-distance:

$$\begin{aligned}&d_3(q,r)=\displaystyle \sup \Big \{ \left| \sum _{x\in X}f(x)q(\{x\}) - \sum _{x\in X}f(x)r(\{x\})\right| :\; \nonumber \\&\qquad f\in L^1(X,\mathcal{S},p),\; \Vert f\Vert _1\le 1 \Big \} \end{aligned}$$

(26)

$\Vert \cdot \Vert _{\infty }$-distance of density functions:

$$\begin{aligned} d_4(q,r) = \displaystyle \sup _{x\in X}\left| \frac{dq}{dp}(x) - \frac{dr}{dp}(x) \right| \end{aligned}$$

(27)

Hellinger distance:

$$\begin{aligned} d_5(q,r) =\displaystyle \sum _{x\in X}\left( \left( \sqrt{\frac{dq}{dp}(x)}-\sqrt{\frac{dr}{dp}(x)} \right) ^2\cdot p(x)\right) \end{aligned}$$

(28)

Euclidean distance:

$$\begin{aligned} d_6(q,r) =\displaystyle \left( \sum _{x\in X}\left( q(\{x\})-r(\{x\})\right) ^{2}\right) ^{\frac{1}{2}} \end{aligned}$$

(29)

Two metrics d and $d'$ on a set M are said to be equivalent if there are constants A and B such that

$$\begin{aligned} A\cdot d(x,y) \le d'(x,y) \le B\cdot d(x,y)\quad \text { for all } x, y\in M \end{aligned}$$

Equivalent metrics generate the same topology on M [see Carothers (2000, p. 121)].

Proposition 8.2

$d_i$ generate the same topology on $M(\mathcal{S})$ for all $i=0\ldots 6$.

Proof

It is straightforward to check $d_0 \le 2d_1\le |X|d_0$. That $d_0$ and $d_6$ are equivalent follows from $d_0 \le d_6 \le 2d_1$. Next, we show $d_1 = d_2$. Let $A = \{x\in X:\; q(\{x\})\ge r(\{x\})\}$. Then

$$\begin{aligned} d_1(q,r)= & {} \frac{1}{2}\sum _{x\in X}\left| q(\{x\})-r(\{x\}) \right| \\= & {} \frac{1}{2}\left( \sum _{x\in A}q(\{x\})-r(\{x\}) + \sum _{x\in X\setminus A} r(\{x\})-q(\{x\}) \right) \\= & {} \frac{1}{2}\left( q(A)-r(A) + r(X\setminus A)-q(X\setminus A) \right) = q(A)-r(A) \\= & {} \max _{E\subseteq X}\left| q(E)-r(E)\right| = d_2(q,r). \end{aligned}$$

That $d_1$ and $d_5$ are equivalent follows from the Cauchy–Schwartz inequality:

$$\begin{aligned} d_1(q,r) \le 2 d_5(q,r) \le 2d_1(q,r)^{1/2} \end{aligned}$$

Next, we claim $d_3=d_4$. Any probability measure q on $\mathcal{S}$ defines a linear functional $\phi _q$ on $L^{1}(X,\mathcal{S},p)$ by assigning to any $f\in L^{1}(X,\mathcal{S},p)$ its expectation value with respect to q:

$$\begin{aligned} \phi _q(f) = \int _{X}f dq = \sum _{x\in X}f(x)q(\{x\}) \end{aligned}$$

The space $L^{1}(X,\mathcal{S},p)^*$ of all linear functionals on $L^{1}(X,\mathcal{S},p)$ is a normed space with the norm $\Vert \phi \Vert$ defined by

$$\begin{aligned} \Vert \phi \Vert = \sup _{\Vert f\Vert _1\le 1}\left| \phi (f)\right| \end{aligned}$$

Recall (see e.g. Chapter 3 in Rudin 1987) that the space $L^{1}(X,\mathcal{S},p)^*$ is isomorphic to $L^{\infty }(X,\mathcal{S},p)$ (with the $\Vert \cdot \Vert _{\infty }$-norm); that is, there is an isometric isomorphism $h: L^{1}(X,\mathcal{S},p)^*\rightarrow L^{\infty }(X,\mathcal{S},p)$. The h-image of $\phi _q$ is the Radon–Nikodym derivative $\frac{dq}{dp}$ of q. Now, we have

$$\begin{aligned} d_3(q,r)= & {} \sup _{\Vert f\Vert _1\le 1}\left| \int f dq - \int f dr \right| = \sup _{\Vert f\Vert _1\le 1}\left| \phi _q(f)-\phi _r(f)\right| \\= & {} \Vert \phi _q-\phi _r\Vert = \Vert h(\phi _q)-h(\phi _r)\Vert _{\infty } = \sup _{x\in X}\left| \frac{dq}{dp}(x)-\frac{dr}{dp}(x)\right| = d_4(q,r) \end{aligned}$$

To complete the proof it is enough to show that $d_1$ and $d_3$ are equivalent.

$$\begin{aligned}&d_1(q,r)\\&\quad = d_2(q,r) = \sup _{E\subseteq X} \left| \int \chi _E dq - \int \chi _E dr \right| \ \overset{\Vert \chi _E\Vert _1\le 1}{\le } \ \sup _{\Vert f\Vert _1\le 1} \left| \int f dq - \int f dr \right| \\&\quad = \sup _{\Vert f\Vert _1\le 1}\left| \sum _{x\in X}f(x)(q(\{x\})-r(\{x\}))\right| \le \sup _{\Vert f\Vert _1\le 1}\sum _{x\in X}|f(x)||(q(\{x\})-r(\{x\}))| \\&\quad = \sup _{\Vert f\Vert _1\le 1}\left( \sum _{x\in X}|f(x)| \cdot \sum _{x \in X}|q(\{x\})-r(\{x\})|\right) \le 2d_1(q,r)\cdot \sup _{\Vert f\Vert _1\le 1} \sum _{x\in X} |f(x)| \end{aligned}$$

Now $\Vert f\Vert _1\le 1$ means $\sum _{x\in X}|f(x)|p(x)\le 1$ and thus there is a constant (depending only on p) such that $\sum _{x\in X}|f(x)|\le K$ holds for all $\Vert f\Vert _1\le 1$. Therefore we obtained

$$\begin{aligned} d_1(q,r) \le d_3(q,r) \le 2Kd_1(q,r) \end{aligned}$$

which completes the proof. $\square$

Recall that for finite X, a sequence $(q_n)\subseteq M(\mathcal{S})$ of measures is said to weak${}^{*}$-converge [cf. Billingsley (1995, p. 335)] to $q\in M(\mathcal{S})$ if for all $f:X\rightarrow {\mathbb {R}}$ we have

$$\begin{aligned} \left| \sum _{x\in X}f(x)\big (q_n(\{x\}) - q(\{x\})\big ) \right| \longrightarrow 0\quad \text { as } n\rightarrow \infty \end{aligned}$$

The topology of weak${}^{*}$-convergence is the same as the topology generated by $d_1$ (and hence by any of the $d_i$’s). Indeed, suppose $q_n$ weak${}^{*}$-converges to q. Choose $f=1$. Then

$$\begin{aligned} \left| \sum _{x\in X}\big (q_n(\{x\}) - q(\{x\})\big ) \right| = 2d_1(q_n,q) \longrightarrow 0\quad \text { as } n\rightarrow \infty \end{aligned}$$

Thus we see that it does not matter which of the metrics $d_i$ we use when studying topological properties of $M(\mathcal{S})$. For convenience we let $(M(\mathcal{S}), d)$ to be a metric space with

$$\begin{aligned} d(q,r) = \max _{x\in X}\left| q(\{x\})-r(\{x\})\right| \end{aligned}$$

Later we will need the following Lemma, proof of which is left to the reader.

Lemma 8.3

For all $\varepsilon >0$ there is $\delta >0$ such that

$$\begin{aligned} \max _{x\in X}\left| q(\{x\})-r(\{x\})\right|<\delta \quad \Longrightarrow \quad \max _{x\in X}\left| \frac{q(x)}{p(x)}-\frac{r(x)}{p(x)}\right| <\varepsilon . \end{aligned}$$

1.2 Proof of Proposition 4.2

Proof

Recall that q is not Bayes learnable if and only if $\frac{dq}{dp}$ is injective (Proposition 3.1). Also recall that the Radon–Nikodym derivative $\frac{dq}{dp}$ is the function $x\mapsto \frac{q(\{x\})}{p(\{x\})}$. Let BBS(p) denote the Bayes p-Blind Spot.

BBS(p) is open: Take any $q\in BBS(p)$. We shall prove that there is $\delta >0$ such that for any $q'\in M(\mathcal{S})$ with $d(q,q')<\delta$ we have $q'\in BBS(p)$. Since $q\in BBS(p)$ the density function $\frac{dq}{dp}$ is not injective. It is enough to prove that for small enough $\delta$, if $d(q,q')<\delta$, then $\frac{dq'}{dp}$ is not injective. Let

$$\begin{aligned} \varepsilon =\frac{1}{2} \min _{x\ne y}\left| \frac{q(\{x\})}{p(\{x\})} - \frac{q(\{y\})}{p(\{y\})}\right| \end{aligned}$$

be the half of the minimal difference of different values of $\frac{dq}{dp}$. Injectivity of $\frac{dq}{dp}$ implies $\varepsilon > 0$. Using Lemma 8.3 there is $\delta >0$ such that

$$\begin{aligned} d(q,q')<\delta \quad \text { implies }\quad \max _{x\in X}\left| \frac{q(x)}{p(x)}-\frac{q'(x)}{p(x)}\right| <\varepsilon \end{aligned}$$

And this latter inequality ensure that $\frac{dq'}{dp}$ must be injective and thus $q'\in BBS(p)$.

BBS(p) is dense: We need to verify that for all $q\in M(\mathcal{S})$ and $\delta >0$ there is $q'\in BBS(p)$ such that $d(q,q')<\delta$. Let us fix q and $\delta$ and chose a function $\varepsilon :X\rightarrow (-\delta ,\;\delta )$ such that $\sum _{x\in X}\varepsilon (x) = 0$ and if $q(\{x\})=0$, then $\varepsilon (x)>0$. Define the measure $q'$ on the singletons $x\in X$ by

$$\begin{aligned} q'(\{x\}) = q(\{x\}) + \varepsilon (x)\quad \text { for all } x\in X \end{aligned}$$

Then $q'$ is a probability measure as $\sum _{x\in X}\varepsilon (x) = 0$, and we obtain $d(q,q')<\delta$. It is straightforward to see that $\varepsilon$ can be chosen in such a manner that

$$\begin{aligned} \frac{q(\{x\})+\varepsilon (x)}{p(\{x\})} \ne \frac{q(\{y\})+\varepsilon (y)}{p(\{y\})}\quad \text { for all } x\ne y\in X \end{aligned}$$

whence injectivity of $\frac{dq'}{dp}$ follows. Therefore $q'\in BBS(p)$ and the proof is complete. $\square$

1.3 Proof of Proposition 4.4

Proof

Let $L\subseteq M$ be the set of Bayes learnable measures. We claim $\lambda ^{n-1}(L) = 0$. $q\in M$ is Bayes learnable if and only if its Radon–Nikodym derivative $\frac{dq}{dp}$ is not injective, i.e.

$$\begin{aligned} L = \left\{ q\in M:\; \frac{q}{p}(x) \text { is not injective}\right\} \end{aligned}$$

Let $\mathcal{A}\subseteq \mathcal{P}(X)$ be a partition of X and call $\mathcal{A}$ a non-trivial partition if $\mathcal{A}\ne \big \{ \{x\}:\; x\in X\}$, i.e. there is at least one block $A\in \mathcal{A}$ that contains at least two elements. Write

$$\begin{aligned} L_{\mathcal{A}} = \left\{ q\in M:\; \frac{q(x)}{p(x)}\text { is constant on every }A\in \mathcal{A}\right\} \;\subseteq \; M \end{aligned}$$

Then we have

$$\begin{aligned} L = \bigcup \left\{ L_{\mathcal{A}}:\; \mathcal{A}\text { is a non-trivial partition of }X\right\} \end{aligned}$$

The proof proceeds as follows: we show that for each non-trivial partition $\mathcal{A}$ the dimension $\dim L_{\mathcal{A}}$ is at most $n-2$. Consequently $\lambda ^{n-1}(L_{\mathcal{A}}) = 0$ and since there are only finitely many partitions of X, we obtain

$$\begin{aligned} \lambda ^{n-1}\left( L \right) = \lambda ^{n-1}\left( \bigcup L_{\mathcal{A}} \right) \le \sum \lambda ^{n-1}\left( L_{\mathcal{A}}\right) = 0 \end{aligned}$$

Take a non-trivial partition $\mathcal{A}$ and pick a block $A\in \mathcal{A}$ in this partition that contains at least two elements, say $x_i$ and $x_j$. For any $q\in L_{\mathcal{A}}$ the function $\frac{dq}{dp}$ should be constant on A. The equation

$$\begin{aligned} \frac{X_i}{p(x_i)} = \frac{X_j}{p(x_j)}\quad (X_i, X_j\in {\mathbb {R}}\text { variables}) \end{aligned}$$

(30)

defines a hyperplane $H'$ and $L_{\mathcal{A}} \subseteq H'$. Clearly none of $H'$ or H contains the other, therefore the intersection $H\cap H'$ has dimension at most $n-2$. Since $L_{\mathcal{A}} \subseteq H\cap H'$, we obtain the desired inequality $\dim L_{\mathcal{A}} \le n-2$ and the proof is complete. $\square$

1.4 Proof of Proposition 5.5

Proof

Let $\mathcal{S}$ be a finite Boolean algebra on set X and $M(\mathcal{S})$ be the set of all probability measures on $\mathcal{S}$. We have to show that for any two probability measures $p_0, p_2$ in $M(\mathcal{S})$ such that $p_2$ is absolutely continuous with respect to $p_0$ there exist two non-trivial partitions $\mathcal{E}, \mathcal{F}$ and probability measures $q,r\in M(\mathcal{S})$ such that using the Jeffrey rule with $p_0$ as prior and with the restriction of q to $\mathcal{E}$ as evidence we obtain a probability measure $p_1$ having the property that, using the Jeffrey rule with $p_1$ as prior and with the restriction of r to $\mathcal{F}$ as evidence we obtain the probability measure $p_2$.

Without loss of generality we may assume that $X = \{a, b, x_1, x_2, \ldots , x_n\}$ is such that $n>1$, and

$$\begin{aligned} p_0(\{a\})\ne 0 \ne p_0(\{b\}) \quad \text { and }\quad p_2(\{a\})\ne 0 \ne p_2(\{b\}) \end{aligned}$$

(31)

and $p_0(\{x_i\})\ne 0$ for at least one $1\le i\le n$. In what follows, for notational convenience we omit the brackets $\{$ and $\}$ in $p_0(\{x_i\})$ etc. whenever this causes no confusion.

Let us define the partitions $\mathcal{E}$ and $\mathcal{F}$ as follows (see also the Fig. 4):

$$\begin{aligned} \mathcal{E}&= \bigg \{ E_1=\{a\},\ E_2=\{b\},\ E_3=\{x_1, x_2, \ldots , x_n\} \bigg \} \end{aligned}$$

(32)

$$\begin{aligned} \mathcal{F}&= \bigg \{ F_0=\{a, b\},\ F_1=\{x_1\}, \ldots ,\ F_{n}=\{x_n\} \bigg \} \end{aligned}$$

(33)

Fig. 4

The non-trivial partition

Note that $p_0$ is non-zero on every element of the partition $\mathcal{E}$. We have to find non-negative numbers $(q_i)$ and $(r_j)$ assigned to the elements $E_i\in \mathcal{E}$ and $F_j\in \mathcal{F}$ of the two partitions such that the measures q and r obtained from these numbers are probability measures and that for all $H\in \mathcal{S}$ we have

$$\begin{aligned} p_1(H)&= q_1\cdot p_0(H\mid E_1) + q_2\cdot p_0(H\mid E_2) + q_3\cdot p_0(H\mid E_3) \end{aligned}$$

(34)

$$\begin{aligned} p_2(H)&= r_0\cdot p_1(H\mid F_0) + \sum _{j\ge 1}r_j\cdot p_1(H\mid F_j) \end{aligned}$$

(35)

Note that for $j\ge 1$ we must have $r_j=p_2(x_j)$ because

$$\begin{aligned} p_2(x_j) = r_j\cdot p_1(x_j\mid F_j) = r_j\cdot \frac{p_1(x_j\cap F_j)}{p_1(F_j)} = r_j\cdot \frac{p_1(F_j)}{p_1(F_j)}=r_j\quad \text { for } j\ge 1 \end{aligned}$$

Thus we only have to find $q_i$ ($i=1,2,3$) and $r_0$. The following are straightforward calculations:

$$\begin{aligned} p_2(a)&= r_0\cdot p_1(a\mid F_0) = r_0\frac{p_1(a)}{p_1(F_0)} = r_0\frac{q_1p_0(a\mid E_1)}{p_1(F_0)} = r_0\frac{q_1}{p_1(F_0)} \end{aligned}$$

(36)

$$\begin{aligned} p_2(b)&= r_0\cdot p_1(b\mid F_0) = r_0\frac{p_1(b)}{p_1(F_0)} = r_0\frac{q_2p_0(b\mid E_2)}{p_1(F_0)} = r_0\frac{q_2}{p_1(F_0)} \end{aligned}$$

(37)

Therefore we must have

$$\begin{aligned} r_0 = \frac{p_2(a)p_1(F_0)}{q_1} = \frac{p_2(b)p_1(F_0)}{q_2} \quad \Longrightarrow \quad \frac{p_2(a)}{q_1} = \frac{p_2(b)}{q_2} \end{aligned}$$

(38)

We can now find the numbers $(q_i)$ ($i=1,2,3$) and $(r_0)$ as follows. Choose $q_1$, $q_2$ and $q_3$ in such a manner that $q_i>0$ and $q_1+q_2+q_3 = 1$, and Eq. (38) holds. With such a choice we have $p_1(E_1)=q_1$, $p_1(E_2)=q_3$ and $p_1(E_3)=q_3$. Next, let $r_j = p_2(x_j)$ for $j\ge 1$ and

$$\begin{aligned} r_0 \doteq \frac{p_2(a)p_1(F_0)}{q_1} \quad \left( = \frac{p_2(b)p_1(F_0)}{q_2}\right) \end{aligned}$$

(39)

$r_0$ is well-defined by the choice of $q_1$ and $q_2$ and by (31) (note that $p_1(F_0) = p_1(E_1)+p_1(E_2)=q_1+q_2>0$). We only need to verify

$$\begin{aligned} r_0+r_1+\cdots +r_n = 1 \end{aligned}$$

(40)

But $r_0=p_2(F_0)$ and thus (40) follows from the fact that $p_2$ is a probability measure: $p_2(F_0)+p_2(x_1)+\cdots +p_2(x_n)=1$. $\square$