Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-31T13:34:01.152Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic classes of finite structures

Published online by Cambridge University Press:  12 March 2014

Richard Elwes
Richard Elwes*
Affiliation:
Department of Mathematics, University of Leeds, Leeds KS2 9JT, UK, E-mail: larry.elwes@gmail.com
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we consider classes of finite structures where we have good control over the sizes of the definable sets. The motivating example is the class of finite fields: it was shown in [1] that for any formula 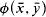in the language of rings, there are finitely many pairs (d, μ) ∈ ω × Q>0 so that in any finite field F and for any ā ∈ Fm the size |ø(Fn,ā)| is “approximately” μ|F|d. Essentially this is a generalisation of the classical Lang-Weil estimates from the category of varieties to that of the first-order-definable sets.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 2 , June 2007 , pp. 418 - 438
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chatzidakis, Z., van den Dries, L., and Macintyre, A., Definable sets over finite fields, Journal für die Reine und Angewandte Mathematik, vol. 427 (1992), pp. 107–135.Google Scholar
[2]Cherlin, G. and Hrushovski, E., Finite structures with few types, Annals of Mathematical Studies, vol. 152, Princeton University Press, 2003.Google Scholar
[3]Hrushovski, E., Unimodular minimal structures, Journal of the London Mathematical Society, Series 2, vol. 46 (1992), pp. 385–396.CrossRefGoogle Scholar
[4]Macpherson, D. and Elwes, R., A survey of asymptotic classes and measurable structures, preprint.Google Scholar
[5]Macpherson, D. and Steinhorn, C., 1-dimensional asymptotic classes and measurable structures, pre-print.Google Scholar
[6]Pillay, A., Geometric stability theory, Oxford Logic Guides, vol. 32. Oxford University Press, 1996.CrossRefGoogle Scholar
[7]Ryten, M., The theory of a pseudofinite field with a fractional power of the Frobenius, Model theory with applications to algebra and analysis, Cambridge University Press, in preparation.Google Scholar
[8]Ryten, M., Results around asymptotic and measurable groups, Ph.D. thesis, University of Leeds, in preparation.Google Scholar
[9]Wagner, F., Simple theories, Mathematics and Its Applications, vol. 503, Kluwer Academic Publishers, 2000.CrossRefGoogle Scholar