Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-27T10:04:51.897Z Has data issue: false hasContentIssue false
  • English
  • Français

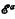-arithmetic and transfinite induction

Published online by Cambridge University Press:  12 March 2014

H. E. Rose
H. E. Rose*
Affiliation:
University of Bristol, Bristol 8, England
Get access Rights & Permissions [Opens in a new window]

Extract

A hierarchy of systems of quantifier-free elementary recursive arithmetics, based on the Grzegorczyk hierarchy of functions, was set up in [2] and some meta-mathematical properties of these systems were developed. The Grzegorczyk hierarchy has been extended recently, mainly by Löb and Wainer [5], and our metamathematical developments may be similarly extended; the αth member of this hierarchy of formal systems will be denoted 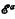-arithmetic throughout. The main result in [2] was: For α > 1, 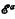-arithmetic can be proved consistent in 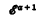-arithmetic. In this paper we shall continue this work in particular, beginning with this consistency result, we shall find (for α > 1) the order type of the weakest simple transfinite induction scheme which is independent of 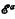-arithmetic, thus giving a ‘measure of the complexity of derivations’ of these systems. For example we shall show that transfinite induction on a sequence of type ωω is a nonderivable rule of primitive recursive arithmetic (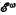-arithmetic). This particular result was proved by Guard in [4] by a specialisation of a version of Gentzen's proof that ∈0-transfinite induction is independent of some standard formal systems of arithmetic with quantifiers. These methods can be adapted to our hierarchy but require what we might term an ‘ωω-jump’—that is if β is the largest ordinal for which transfinite induction up to β is derivable in the system in question then a scheme of transfinite induction up to β·ωω is independent. The proof presented in this paper requires only an ‘ω-jump’ and allows more precise results to be obtained for the systems in the extended Grzegorczyk hierarchy; it is also more direct and less proof-theoretic in character. We show that the consistency of 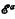-arithmetic (for α > 1) can be proved in a system obtained by adding to 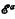-arithmetic a transfinite induction scheme up to ω2, and that this induction scheme can be adapted to obtain the required result by increasing the ordinal and simultaneously decreasing the complexity of the functions involved in the induction scheme (detailed definitions of these concepts will be given in the next section).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 1 , March 1972 , pp. 19 - 30
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Church, A., unpublished notes, 1958.Google Scholar
[2]Cleave, J. P. and Rose, H. E., -arithmetic, Sets, models and recursion theory, ed. Crossley, , North-Holland, Amsterdam, 1967.Google Scholar
[3]Grzegorczyk, A., Some classes of recursive functions, Rozprawy Matematyczne, vol. 4 (1953), pp. 1–43.Google Scholar
[4]Guard, J., The independence of transfinite induction up to ω ω in recursive arithmetic, Ph.D. thesis, Princeton University, 1961.Google Scholar
[5]Löb, M. H. and Wainer, S. S., Hierarchies of number-theoretic functions, (to appear).Google Scholar
[6]Robbin, J. W., Subrecursive hierarchies, Ph.D. thesis, Princeton University, 1965.Google Scholar
[7]Rose, H. E., Ternary recursive arithmetic, Mathematica Scandinavica, vol. 10 (1962), pp. 201–216.CrossRefGoogle Scholar
[8]Rose, H. E., Independence of induction schemas in recursive arithmetic, this Journal, vol. 25 (1960), p. 95.Google Scholar
[9]Rose, H. E., A note on reducible induction schemata, Zeitschrift für Mathematische Logik, vol. 11 (1965), pp. 121–126.CrossRefGoogle Scholar
[10]Wainer, S. S., Hierarchies of number-theoretic functions, Ph.D. thesis, University of Leeds, 1969.Google Scholar