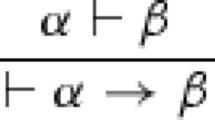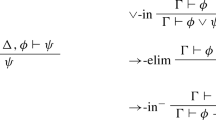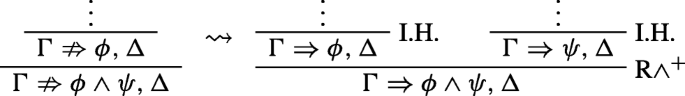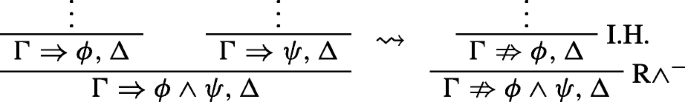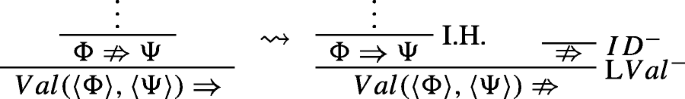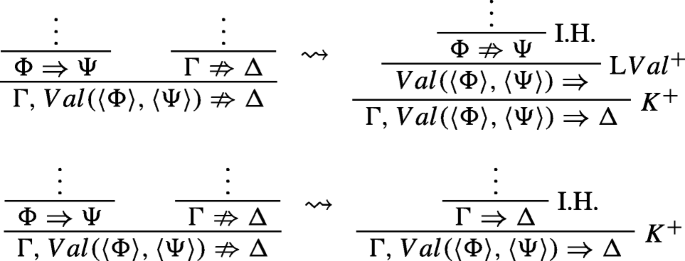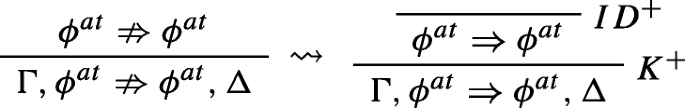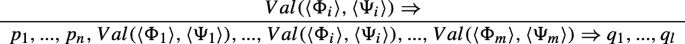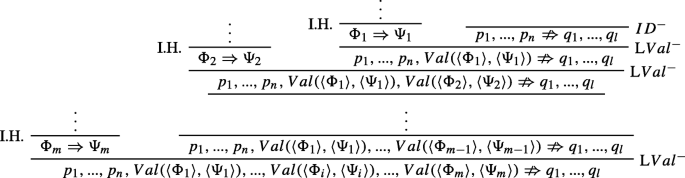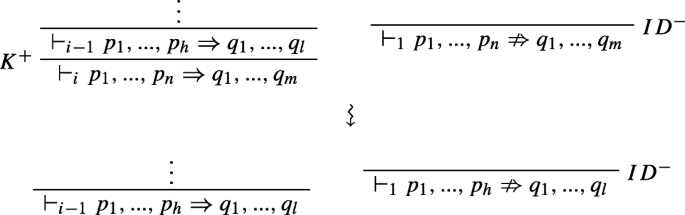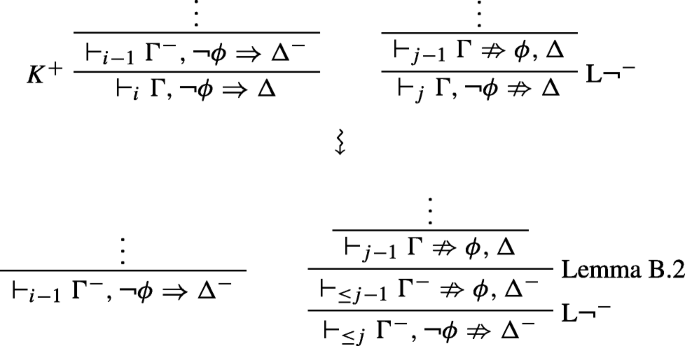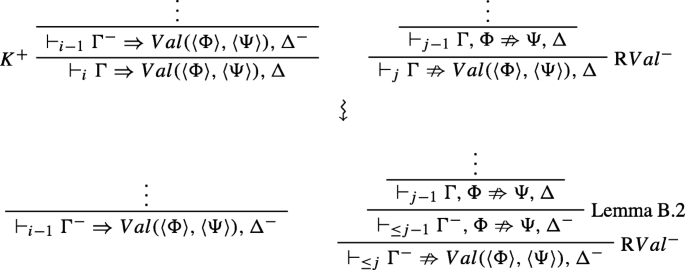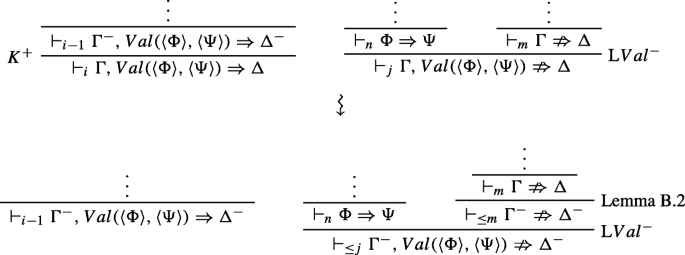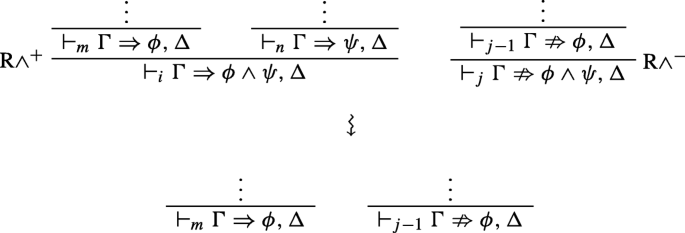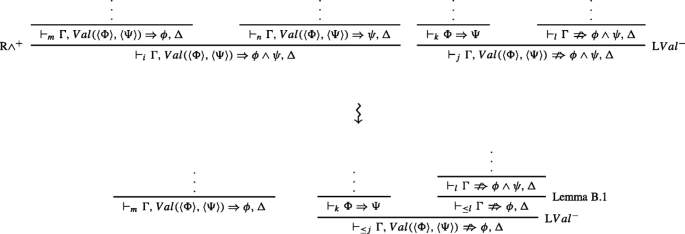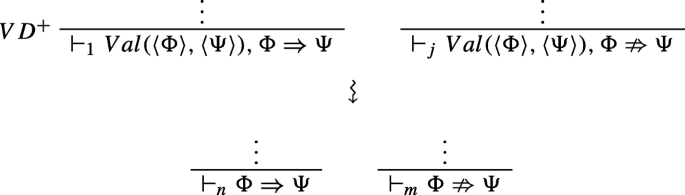Towards a Non-classical Meta-theory for Substructural Approaches to Paradox

Abstract

In the literature on self-referential paradoxes one of the hardest and most challenging problems is that of revenge. This problem can take many shapes, but, typically, it besets non-classical accounts of some semantic notion, such as truth, that depend on a set of classically defined meta-theoretic concepts, like validity, consistency, and so on. A particularly troubling form of revenge that has received a lot of attention lately involves the concept of validity. The difficulty lies in that the non-classical logician cannot accept her own definition of validity because it is given in a classical meta-theory. It is often suggested that this mismatch between the consequence relation of the account being espoused and the consequence relation of the meta-theory is a serious embarrassment. The main goal of the paper is to explore whether certain substructural accounts of the paradoxes can avoid this sort of embarrassment. Typically, these accounts are expressively incomplete, since they cannot assert in the object language that certain invalid arguments are in fact invalid. To overcome this difficulty I develop a novel type of hybrid proof-procedure, one that takes invalidities to be just as fundamental as validities. I prove that this proof-procedure enjoys a number of interesting properties and I analyze the prospects of applying it to languages capable of expressing self-referential statements.

Appendices

Appendix A: The external completeness of ${\mathscr{H}}^{V}_{{\mathscr{L}}}$

We begin with some definitions.

Definition 1

(Rank) The rank of a derivation (or tree) is the total number of nodes in that derivation (or tree), where each node is either a sequent or an anti-sequent.

Definition 2

(Admissibility) A rule is admissible if its conclusion-sequent is derivable whenever its premise-sequent(s) is (are). Similarly for anti-sequents.

Definition 3

(Invertibility) A rule is invertible if its premise-sequent(s) is (are) derivable whenever its conclusion-sequent is derivable. Similarly for anti-sequents.

Definition 4

(Rank-preserving admissibility) A one-premise rule is rank-preserving admissible if whenever the premise-sequent has a derivation of rank k, the conclusion-sequent has a derivation of rank at most k. Mutatis mudantis for rules that involve anti-sequents. (There’s no need to define rank-preserving admissibility for two-premise rules). Of course, if a rule is (rank-preserving) admissible, then there’s no need to consider it in the proofs below.

Definition 5

(Rank-preserving invertibility) A one-premise rule is rank-preserving invertible if whenever the conclusion-sequent has a derivation of rank k, the premise-sequent has a derivation of rank at most k. A two-premise rule is rank-preserving invertible if whenever the conclusion-sequent has a derivation of rank k, the premise-sequents have derivations of ranks i and j, respectively, such that i + j ≤ k. Mutatis mudantis for rules that involve anti-sequents.

Definition 6

(Rank-preserving semi-invertibility) We say that each of a pair of rules with the same conclusion-anti-sequent is rank-preserving semi-invertible if whenever the conclusion-anti-sequent has a derivation of rank k, then the premise-anti-sequent of at least one of the rules has a derivation of rank at most k.

For example, the rules R∧⁻ are rank-preserving semi-invertible if whenever ${\Gamma }\nRightarrow \phi \wedge \psi , {\Delta }$ has a derivation of rank k, then either ${\Gamma }\nRightarrow \phi , {\Delta }$ has a derivation of rank at most k or ${\Gamma }\nRightarrow \psi , {\Delta }$ has a derivation of rank at most k.¹

It is essential to note that the rank of a derivation is different from the height of a derivation. The height of a derivation is typically taken to be the maximum number of successive steps in that derivation. The difference is irrelevant if derivations are linear, but not if derivations are trees. Now, we could use an induction on the height for the proof of external completeness to be given below, but due to the presence of V D⁺ in ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$, we cannot carry out an induction on the height for the proof of its external consistency, also to be given below. I will explain why this is so in due course (see the remarks right after the proof of Theorem B.3).

We can now prove some lemmata:

Lemma A.1 (Invertibility)

The operational rules of ${\mathscr{H}}^{V}_{{\mathscr{L}}}$ are rank-preserving invertible, with the exception of the two rules R∧⁻, which are rank-preserving semi-invertible.

Proof

sketch This is proved by induction on the rank of the derivation of the conclusion-sequent or the conclusion-anti-sequent of the rule. Cf. for instance [50, p. 49] for a proof showing that the usual positive logical rules are height-preserving invertible. It is straightforward to adapt this proof to the notion of rank, to the logical rules involving anti-sequents and to the validity rules; the work is left to the enthusiastic reader. □

Next I will show the admissibility of the anti-weakening rule, K⁻. A bit of notation will be helpful for this. If there is a derivation of the sequent Γ ⇒Δ or the anti-sequent ${\Gamma }\nRightarrow {\Delta }$ with rank k, I will write ⊩_kΓ ⇒Δ and $\vdash _{k}{\Gamma }\nRightarrow {\Delta }$, respectively. The result below was established by Carnielli and Pulcini in [29] for a calculus without validity rules.

Lemma A.2 (Admissibility of K ⁻)

The rule of anti-weakening, K⁻, is rank-preserving admissible in ${\mathscr{H}}^{V}_{{\mathscr{L}}}$.

Proof

sketch

We prove this by induction on the rank of the derivation of the premise-anti-sequent. That is, we assume that $\vdash _{k}{\Gamma }\nRightarrow {\Delta }$ and we need to show that $\vdash _{\leq k}{\Gamma }^{-}\nRightarrow {\Delta }^{-}$, where Γ⁻ is a submultiset of Γ, Δ⁻ is a submultiset of Δ, and one of these inclusions is strict. We have to consider all the ways in which ${\Gamma }\nRightarrow {\Delta }$ might have been obtained.

• If ${\Gamma }\nRightarrow {\Delta }$ is an instance of ID⁻, it is of the form $p_{1},...,p_{n}\nRightarrow q_{1},...,q_{m}$. But, then, whatever ${\Gamma }^{-}\nRightarrow {\Delta }^{-}$ is, it will also be an instance of ID⁻. In both cases the rank is 1.

• For the logical rules and RV al⁻ we use the inductive hypothesis on the premise-sequent. I will only look at the case of R∧⁻ to illustrate how this works. If ${\Gamma }\nRightarrow {\Delta }$ was obtained by an application of R∧⁻, then it has the form $\vdash _{k}{\Gamma }\nRightarrow \phi \wedge \psi , {\Delta }$ and it comes from either $\vdash _{k-1}{\Gamma }\nRightarrow \phi , {\Delta }$ or $\vdash _{k-1}{\Gamma }\nRightarrow \psi , {\Delta }$. Without loss of generality, let’s assume that it comes from the latter. We apply the inductive hypothesis to obtain $\vdash _{\leq k-1}{\Gamma }^{-}\nRightarrow \psi , {\Delta }^{-}$ (or simply $\vdash _{\leq k-1}{\Gamma }^{-}\nRightarrow {\Delta }^{-}$, if this is the conclusion-anti-sequent of the original application of K⁻) and then, if necessary, we apply R∧⁻ to reach $\vdash _{\leq k}{\Gamma }^{-}\nRightarrow \phi \wedge \psi , {\Delta }^{-}$.

• For LV al⁻, ${\Gamma }\nRightarrow {\Delta }$ must be of the form $\vdash _{k}{\Gamma }, Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\nRightarrow {\Delta }$. So, our anti-sequent was obtained by an application of LV al⁻ from the sequent ⊩_iΦ ⇒Ψ and the anti-sequent $\vdash _{j}{\Gamma }\nRightarrow {\Delta }$, such that i < k, j < k and k = j + i + 1. By the inductive hypothesis, $\vdash _{\leq j}{\Gamma }^{-}\nRightarrow {\Delta }^{-}$. Then, if necessary, an application of LV al⁻ yields $\vdash _{\leq k}{\Gamma }^{-}, Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\nRightarrow {\Delta }^{-}$.

□

It is also possible to establish a similar result for the contraction rules, LW⁺ and RW⁺, and for the anti-contraction rules, LW⁻ and RW⁻.

Proposition A.3

The contraction rules, LW⁺ and RW⁺, are rank-preserving admissible in ${\mathscr{H}}^{V}_{{\mathscr{L}}}$, and the anti-contraction rules, LW⁻ and RW⁻, are admissible in ${\mathscr{H}}^{V}_{{\mathscr{L}}}$.

This proposition is not relevant for the result below, so its proof is left to the reader. Note that I am claiming that the anti-contraction rules are merely admissible and not rank-preserving admissible. For example, there is a derivation of $\neg \neg p\nRightarrow$ with rank 3, but the shortest derivation of $\neg \neg p, \neg \neg p\nRightarrow$ that doesn’t require an application of LW⁻ has rank 5:

Now we are ready to prove external completeness.

Theorem A.4

${\mathscr{H}}^{V}_{{\mathscr{L}}}$ is externally complete. That is, for every multiset Γ and every multiset Δ, either Γ ⇒Δ has a derivation in ${\mathscr{H}}^{V}_{{\mathscr{L}}}$ or ${\Gamma }\nRightarrow {\Delta }$ has a derivation in ${\mathscr{H}}^{V}_{{\mathscr{L}}}$.

Proof sketch

The idea of the proof is to take any sequent, Γ ⇒Δ, or anti-sequent, ${\Gamma }\nRightarrow {\Delta }$, and construct a ‘reduction tree’ for it following a certain set of instructions.² At the first stage we have a sequent, Γ ⇒Δ, or an anti-sequent, ${\Gamma }\nRightarrow {\Delta }$, that is the root of our tree. This is reduced by taking each statement in it (in a certain order) and, roughly, applying the rules of the calculus backwards, that is, from bottom to top. As the tree is extended, sometimes the tip of a branch is an instance of ID⁺ or ID⁻. If so, we say that the branch is closed. If a branch is not closed, it is open. At each successive stage, we apply certain steps to reduce each statement in the tip of each open branch, with the exception of statements that have been produced during the stage itself; those get reduced at the next stage. More specifically:

• 1. Identity: If at some point one reaches a sequent, Γ,ϕ^at ⇒ ϕ^at,Δ, or anti-sequent, ${\Gamma }, \phi ^{at}\nRightarrow \phi ^{at}, {\Delta }$, then one extends the branch with ϕ^at ⇒ ϕ^at or with $\phi ^{at}\nRightarrow \phi ^{at}$.

• 2. Negation: To reduce ¬ϕ on the right in a sequent Γ ⇒¬ϕ,Δ, one extends the branch with Γ,ϕ ⇒Δ. To reduce ¬ϕ in an anti-sequent ${\Gamma }\nRightarrow \neg \phi , {\Delta }$ one extends the branch with ${\Gamma }, \phi \nRightarrow {\Delta }$. For negations on the left of sequents or anti-sequents, the procedure is similar.

• 3. Conjunction: To reduce ϕ ∧ ψ on the left in a sequent Γ,ϕ ∧ ψ ⇒Δ, one extends the branch with Γ,ϕ,ψ ⇒Δ. Similarly for ϕ ∧ ψ on the left of an anti-sequent. To reduce ϕ ∧ ψ on the right in a sequent Γ ⇒ ϕ ∧ ψ,Δ, one branches upwards, writing Γ ⇒ ϕ,Δ and Γ ⇒ ψ,Δ. To reduce ϕ ∧ ψ on the right in an anti-sequent ${\Gamma }\nRightarrow \phi \wedge \psi , {\Delta }$, one must consider two different trees, one for each conjunct! In one of them, one extends the branch with ${\Gamma }\nRightarrow \phi , {\Delta }$. In the other, one extends the branch with ${\Gamma }\nRightarrow \psi , {\Delta }$.³

• 4. Validity: To reduce V al(〈Φ〉,〈Ψ〉) on the right in a sequent Γ ⇒ V al(〈Φ〉,〈Ψ〉),Δ, one extends the branch with Γ,Φ ⇒Ψ,Δ. Similarly for V al(〈Φ〉,〈Ψ〉) on the right in an anti-sequent. To reduce V al(〈Φ〉,〈Ψ〉) on the left in an anti-sequent ${\Gamma }, Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\nRightarrow {\Delta }$, one branches upwards, writing Φ ⇒Ψ and ${\Gamma }\nRightarrow {\Delta }$. To reduce V al(〈Φ〉,〈Ψ〉) on the left in a context-free sequent V al(〈Φ〉,〈Ψ〉) ⇒, one extends the branch upwards with ${\Phi }\nRightarrow {\Psi }$ (if the context is not free, see instruction 5).

Note that these instructions still don’t tell us how to reduce sequents like Γ,V al(〈Φ〉,〈Ψ〉) ⇒Δ when Γ and/or Δ are non-empty. For this reason, we need one additional instruction.

• 5. Weakening: If at some point one reaches a sequent Γ,V al(〈Φ〉,〈Ψ〉) ⇒Δ with Γ and/or Δ non-empty, where Γ (if non-empty) only contains propositional variables and/or validity predications, and Δ (if non-empty) only contains propositional variables, then one must consider possibly several different trees, one for each statement of the form V al(〈Φ〉,〈Ψ〉). In each of these trees one extends the branch with V al(〈Φ〉,〈Ψ〉) ⇒.

Instruction 1 takes priority over the other ones. There are many ways to obtain a tree (or a set of trees) from a given sequent (anti-sequent) following these instructions. Here, for definiteness, we can use the fact that there is an enumeration of the statements of ${\mathscr{L}}$. The reduction can proceed following this enumeration, so that at each stage one reduces all the statements in the sequent (anti-sequent) starting with the one with the lowest number according to the enumeration, and then continuing in the obvious way. In case a statement occurs both in the left and right hand side of a sequent (anti-sequent), then the left occurrence gets reduced first. And if a statement occurs more than once in the antecedent or consequent of a sequent (anti-sequent), then it doesn’t matter which occurrence gets reduced first.

At some stage we will reach a set of trees with leaves that are sequents and/or anti-sequents composed solely of propositional variables. These are maximal trees, that is, trees where the leaves cannot be further reduced. If, in one of the trees, the leaves in every one of its branches are either sequents of the form ϕ^at ⇒ ϕ^at, or anti-sequents of the form $\phi ^{at}_{1},...,\phi ^{at}_{n}\nRightarrow \psi ^{at}_{1},...,\psi ^{at}_{m}$ (where all the propositional variables on the left are different from all the propositional variables on the right), then one has obtained a derivation of the original sequent/anti-sequent. If, instead, this doesn’t occur in any of the trees, there will be at least one open branch in every maximal tree. The idea is that one can take the open branch in any of these trees and, as it were, use the materials in the branch to obtain a derivation of the corresponding anti-sequent/sequent.⁴ The transformation procedure is quite simple. In most cases one just transforms sequents Γ ⇒Δ into the corresponding anti-sequents ${\Gamma }\nRightarrow {\Delta }$ and vice versa.

We define the height of a branch in a tree as the total number of nodes in the branch. For branches of height 1, the transformation is straightforward. We replace the sequent/anti-sequent with the corresponding anti-sequent/sequent, thus obtaining either an instance of ID⁺ or an instance of ID⁻. For branches of height greater than 1, we need an induction on the height. So the idea is to assume that the transformation can be done for trees with open branches of height less than k, and what we need to show is that it can be done for trees with open branches of height k as well. A bit more precisely, the structure of the (rest of) proof is this. The inductive hypothesis is that the transformation can be done for trees with open branches of height less than k; this yields the more general claim that for every tree with open branches of height less than k, there is a tree ending with the “reverse” conclusion which has no open branches. In other words:

• For every tree with the sequent Γ ⇒Δ (anti-sequent ${\Gamma }\nRightarrow {\Delta }$) at the root, in which all the open branches have height less than k, there is a tree which has no open branches, with the anti-sequent ${\Gamma }\nRightarrow {\Delta }$ (sequent Γ ⇒Δ) at the root.

Hence, if it can be shown that the transformation can be done for trees with open branches of height k as well, this, in turn, will yield the more general claim that for every tree with open branches of height k, there is a tree ending with the “reverse” conclusion which has no open branches. In other words:

• For every tree with the sequent Γ ⇒Δ (anti-sequent ${\Gamma }\nRightarrow {\Delta }$) at the root, in which all the open branches have height at most k, there is a tree which has no open branches, with the anti-sequent ${\Gamma }\nRightarrow {\Delta }$ (sequent Γ ⇒Δ) at the root.

Now, for every application of a rule in an open branch, we proceed by replacing the sequents/anti-sequents with the corresponding anti-sequents/sequents. In many cases, this is enough to obtain what we want. The only exceptions are the five rules R∧⁺, R∧⁻, LV al⁺, LV al⁻, and K⁺.

• In the case of R∧⁻, there is a tree with an open branch containing the anti-sequent ${\Gamma }\nRightarrow \phi , {\Delta }$ and another tree with an open branch containing the anti-sequent ${\Gamma }\nRightarrow \psi , {\Delta }$. In both cases the anti-sequent is immediately followed by ${\Gamma }\nRightarrow \phi \wedge \psi , {\Delta }$. Let’s assume without loss of generality that the open branch with greater height is the one containing ${\Gamma }\nRightarrow \phi , {\Delta }$, and that its height is k. By the inductive hypothesis we know that there must be a derivation for Γ ⇒ ϕ,Δ. But, also, we know that there must be a derivation for Γ ⇒ ψ,Δ, since there is an open branch containing the corresponding anti-sequent, ${\Gamma }\nRightarrow \psi , {\Delta }$, and its height is less than k. The result of the transformation is an application of R∧⁺.

  

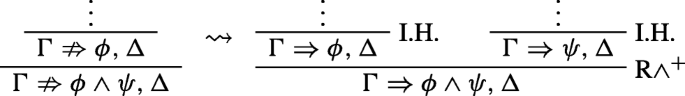
• For R∧⁺, we take the open branch and perform the transformations. The result is an application of one of the R∧⁻ rules. Thus, if we assume without loss of generality that the open branch is the one that contains Γ ⇒ ϕ,Δ, we have:

  

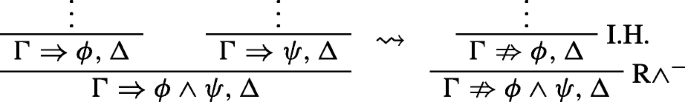
• For an application of LV al⁺ in an open branch, we transform the premise-anti-sequent in a sequent and the conclusion-sequent in an anti-sequent. Then we add the empty anti-sequent, $\nRightarrow$, as an additional premise. The result is an application of LV al⁻.

  

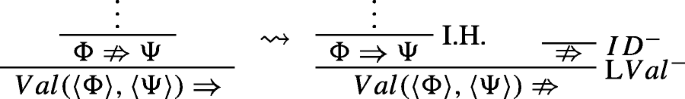
• In the case of LV al⁻, if the open branch contains the left premise-sequent, then the result of the transformation is an application of LV al⁺. We may then apply K⁺, if necessary. If, instead, the open branch contains the right premise-anti-sequent, then, after the transformation, the result is an application of K⁺.

  

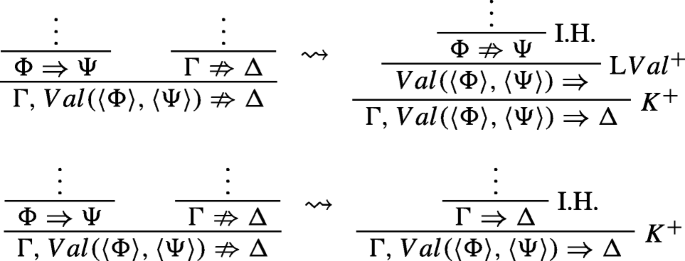
• Lastly, as per instructions 1 and 5 above, there are two other cases that we need to take care of. The first type of case involves instances of identity with weakening ‘built in’. What we do in such cases is just to replace anti-sequents by sequents. The resulting step can be justified by K⁺.

  

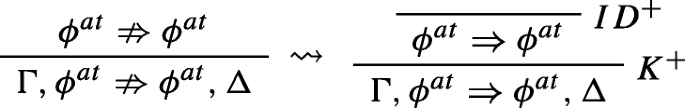
  The second type of case involves occurrences of validity predications on the left of a sequent.

  

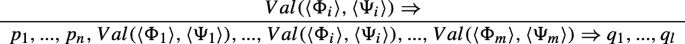
  Here the idea is to replace the single step above with the following derivation:

  

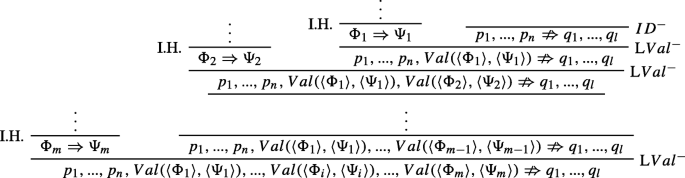
  That this replacement is legitimate can be seen as follows. By the inductive hypothesis we can assume that there is a way to perform the transformation for the branch with root V al(〈Φ_i〉,〈Ψ_i〉) ⇒, for each one of the trees corresponding to each of the statements of the form V al(〈Φ_i〉,〈Ψ_i〉). Thus, we can assume that there is a derivation of the sequent $Val(\langle {\Phi }_{i}\rangle , \langle {\Psi }_{i}\rangle )\nRightarrow$, for each Φ_i and each Ψ_i. By the invertibility of LV al⁻, we can infer that there is a derivation of Φ_i ⇒Ψ_i, for each Φ_i and each Ψ_i.

□

Appendix B: The external consistency of ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$ and ${\mathscr{H}}^{V}_{{\mathscr{L}}}$

It is more convenient to prove the external consistency of the calculus ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$ first, and to obtain the external consistency of ${\mathscr{H}}^{V}_{{\mathscr{L}}}$ as a corollary. We need to be careful, though. The presence of V D⁺ in ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$ has, as an effect, that the invertibility of the positive rules breaks down. For example, ¬π,V al(〈¬π〉,〈p〉) ⇒ p has a derivation in ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$, but V al(〈¬π〉,〈p〉) ⇒ π,p does not, so L¬⁺ is not invertible. In any case, the negative rules of ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$ are still rank-preserving invertible, and, fortunately, we only need the invertibility of these rules for the proof of external consistency.

Lemma B.1 (Invertibility)

All the negative rules are rank-preserving invertible in ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$, with the exception of the two rules R∧⁻ which are rank-preserving semi-invertible.

Similarly, we can still show that the anti-weakening rule is rank-preserving admissible.

Lemma B.2 (Admissibility)

The anti-weakening rule, K⁻, is rank-preserving admissible in ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$.

To prove that ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$ is externally consistent, we need the following additional definition:

Definition 7

(Combined rank) Given two derivations with ranks n and m, respectively, we say that the combined rank of these two derivations is n + m.

Theorem B.3 (External consistency)

${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$ is externally consistent. That is, for every multiset Γ and every multiset Δ, it is not the case that Γ ⇒Δ and ${\Gamma }\nRightarrow {\Delta }$ are both derivable in ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$.

Proof sketch

The proof is by induction on the combined rank of the derivations of the sequent Γ ⇒Δ and the anti-sequent ${\Gamma }\nRightarrow {\Delta }$. The strategy is as follows. First, we observe that there cannot be an external inconsistency between an instance of ID⁺ and an instance of ID⁻. Next, we assume that there is an external inconsistency at a certain combined rank k between a sequent Γ ⇒Δ and an anti-sequent ${\Gamma }\nRightarrow {\Delta }$, i.e., we assume that ⊩_iΓ ⇒Δ and $\vdash _{j}{\Gamma }\nRightarrow {\Delta }$, where i + j = k. Then we show how to produce another external inconsistency with a combined rank lower than k. That is, we show that ⊩_mπ ⇒Σ and $\vdash _{n}{\Pi }\nRightarrow {\Sigma }$, where π is possibly different from Γ, Σ is possibly different from Δ, and m + n < i + j. In other words, what we are doing is to “move the external inconsistency up”, in the same way that in a cut-elimination proof we “move the cut up”. This is done until we reach an external inconsistency between an instance of ID⁺ and an instance of ID⁻, which we know is not possible.

As expected, there are many cases to consider, since we have to take care of all of the ways in which Γ ⇒Δ and ${\Gamma }\nRightarrow {\Delta }$ might have been derived. I will only look at a few. Naturally, given that Lemma B.2 tells us that K⁻ is an admissible rule, we can ignore it.

• If Γ ⇒Δ is an instance of ID⁺, then it is of the form p ⇒ p. Clearly, ${\Gamma }\nRightarrow {\Delta }$ cannot be an instance of ID⁻, since instances of ID⁻ cannot be of the form $p\nRightarrow p$. Also, it could not have been obtained by an application of a logical rule, or by an application of a validity rule. Thus, there cannot be an external inconsistency in this case.

• If the sequent Γ ⇒Δ is a result of applying the rule L⊥⁺, then it is ⊥⇒. It is clear that no external inconsistency can be generated in this case either, for no derivation of $\bot \nRightarrow$ is available.

• If the sequent Γ ⇒Δ was obtained from Γ⁻⇒Δ⁻ by an application of the rule K⁺, where Γ⁻ is a submultiset of Γ and Δ⁻ is a submultiset of Δ, we have to consider all the ways in which the anti-sequent ${\Gamma }\nRightarrow {\Delta }$ could have been obtained.

  • If ${\Gamma }\nRightarrow {\Delta }$ is an instance of ID⁻, then it is of the form $p_{1},...,p_{n}\nRightarrow q_{1},...,q_{m}$, and thus we have ⊩_ip₁,...,p_n ⇒ q₁,...,q_m and $\vdash _{1} p_{1},...,p_{n}\nRightarrow q_{1},...,q_{m}$. But since Γ⁻ is a submultiset of Γ and Δ⁻ is a submultiset of Δ, Γ⁻⇒Δ⁻ has a derivation of rank less than i and it is already externally inconsistent with another instance of ID⁻, say, ⊩_i− 1p₁,...,p_h ⇒ q₁,...,q_l, where Γ⁻ = p₁,...,p_h is a submultiset of Γ and Δ⁻ = q₁,...,q_l is a submultiset of Δ. This means that the combined rank of their derivations is less than the combined rank of the original derivations.

    

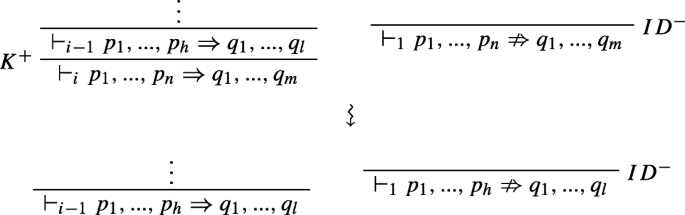
  • ${\Gamma }\nRightarrow {\Delta }$ was obtained by the application of some logical rule. Here I will only consider the rule L¬⁻, to illustrate how this works; the other rules can be treated similarly. If the last rule applied was L¬⁻, then ${\Gamma }\nRightarrow {\Delta }$ must be of the form ${\Gamma }, \neg \phi \nRightarrow {\Delta }$ and so we have ⊩_iΓ,¬ϕ ⇒Δ and $\vdash _{j} {\Gamma }, \neg \phi \nRightarrow {\Delta }$, where i + j = k. The anti-sequent was obtained from $\vdash _{j-1}{\Gamma }\nRightarrow \phi , {\Delta }$ and the sequent was obtained by an application of K⁺ from either ⊩_i− 1Γ ⇒Δ or $\vdash _{i-1}{\Gamma }^{-}, \neg \phi \Rightarrow {\Delta }^{-}$. In the former case, we just apply K⁺ to obtain ⊩_iΓ ⇒ ϕ,Δ. In the latter case, we use Lemma B.2. Since K⁻ is rank-preserving admissible and $\vdash _{j-1}{\Gamma }\nRightarrow \phi , {\Delta }$, we also have $\vdash _{\leq j-1}{\Gamma }^{-}\nRightarrow \phi , {\Delta }^{-}$. Then we can use L¬⁻ to obtain $\vdash _{\leq j}{\Gamma }^{-}, \neg \phi \nRightarrow {\Delta }^{-}$. In both cases we have an external inconsistency and the combined rank has been reduced. The latter case can be graphically depicted as follows:

    

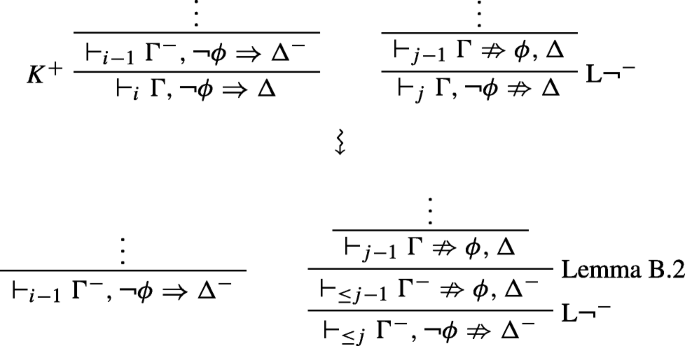
  • ${\Gamma }\nRightarrow {\Delta }$ is of the form $\vdash _{j}{\Gamma }\nRightarrow Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle ), {\Delta }$ and it was obtained by an application of RV al⁻ from $\vdash _{j-1}{\Gamma }, {\Phi }\nRightarrow {\Psi }, {\Delta }$. Then, our original sequent is of the form ⊩_iΓ ⇒ V al(〈Φ〉,〈Ψ〉),Δ and it comes from either ⊩_i− 1Γ ⇒Δ or $\vdash _{i-1}{\Gamma }^{-}\Rightarrow Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle ), {\Delta }^{-}$ by K⁺. In the former case, we apply K⁺ to obtain ⊩_iΓ,Φ ⇒Ψ,Δ. In the latter case, we use Lemma B.2. Since K⁻ is rank-preserving admissible and $\vdash _{j-1}{\Gamma }, {\Phi }\nRightarrow {\Psi }, {\Delta }$, we also have $\vdash _{\leq j-1}{\Gamma }^{-}, {\Phi }\nRightarrow {\Psi }, {\Delta }^{-}$. Then, we apply RV al⁻ to obtain $\vdash _{\leq j}{\Gamma }^{-}\nRightarrow Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle ), {\Delta }^{-}$. In both cases we have an external inconsistency and the combined rank has been reduced. The latter case can be graphically depicted as follows:

    

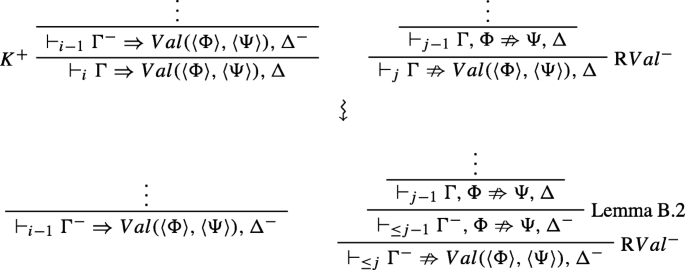
  • ${\Gamma }\nRightarrow {\Delta }$ is of the form $\vdash _{j}{\Gamma }, Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\nRightarrow {\Delta }$ and was obtained by an application of LV al⁻ from the sequent ⊩_nΦ ⇒Ψ and the anti-sequent $\vdash _{m}{\Gamma }\nRightarrow {\Delta }$, where n + m + 1 = j. Then, our original sequent must be of the form ⊩_iΓ,V al(〈Φ〉,〈Ψ〉) ⇒Δ and was obtained either from ⊩_i− 1Γ ⇒Δ or from $\vdash _{i-1}{\Gamma }^{-}, Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\Rightarrow {\Delta }^{-}$. In the former case, we have already reached an external inconsistency. In the latter case, we apply Lemma B.2 to $\vdash _{m}{\Gamma }\nRightarrow {\Delta }$ in order to obtain $\vdash _{\leq m}{\Gamma }^{-}\nRightarrow {\Delta }^{-}$. Then, an application of LV al⁻ delivers $\vdash _{\leq j}{\Gamma }^{-}, Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\nRightarrow {\Delta }^{-}$, so we have an external inconsistency. In both cases the combined rank was reduced. The latter case can be graphically depicted as follows:

    

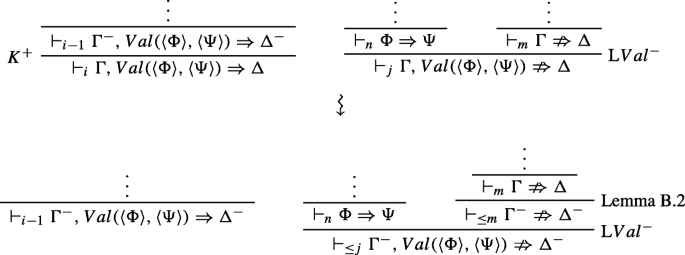
• The sequent Γ ⇒Δ was obtained by one of the logical rules L¬⁺, R¬⁺, L∧⁺ or R∧⁺. These cases, which do not present much difficulties, require our previous result on the rank-preserving invertibility of the negative rules (Lemma B.1). In each case we have to consider the different ways in which the corresponding anti-sequent ${\Gamma }\nRightarrow {\Delta }$ could have been obtained. To illustrate, I will just consider the case in which Γ ⇒Δ is of the form Γ ⇒ ϕ ∧ ψ,Δ and was obtained from Γ ⇒ ϕ,Δ and Γ ⇒ ψ,Δ by an application of the rule R∧⁺. Then, the anti-sequent ${\Gamma }\nRightarrow {\Delta }$ must be of the form ${\Gamma }\nRightarrow \phi \wedge \psi , {\Delta }$.

  • Clearly, ${\Gamma }\nRightarrow \phi \wedge \psi , {\Delta }$ cannot be an instance of ID⁻. If $\vdash _{j}{\Gamma }\nRightarrow \phi \wedge \psi , {\Delta }$ was obtained by an application of some negative rule, then there are two cases to consider. Either ϕ ∧ ψ is principal or it is not. If it is, then the anti-sequent was obtained by an application of R∧⁻ to $\vdash _{j-1}{\Gamma }\nRightarrow \phi , {\Delta }$ or to $\vdash _{j-1}{\Gamma }\nRightarrow \psi , {\Delta }$. Let’s assume, without loss of generality, that it was obtained from the former. Then the external inconsistency can be transformed in the following way:

    

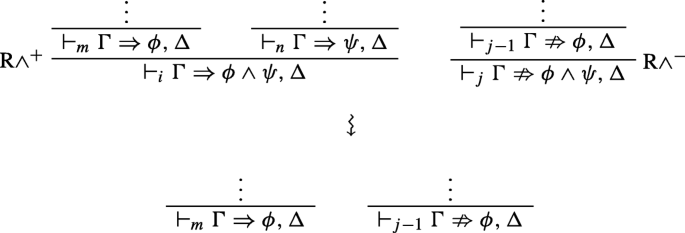
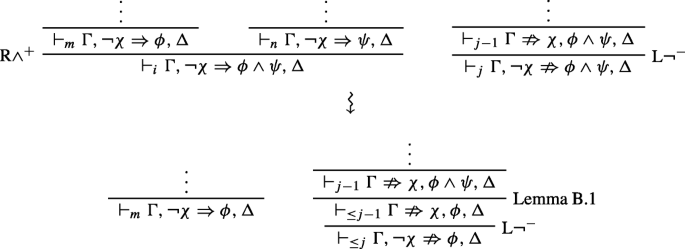
  • If it is not principal, we need to use Lemma B.1, which guarantees the rank-preserving semi-invertibility of the R∧⁻ rules. To illustrate how, I will just take a look at the cases of L¬⁻ and LV al⁻. In the first case, $\vdash _{j}{\Gamma }\nRightarrow \phi \wedge \psi , {\Delta }$ is of the form $\vdash _{j}{\Gamma }, \neg \chi \nRightarrow \phi \wedge \psi , {\Delta }$ and it comes from $\vdash _{j-1}{\Gamma }\nRightarrow \chi , \phi \wedge \psi , {\Delta }$. Our original sequent is then of the form ⊩_iΓ,¬χ ⇒ ϕ ∧ ψ,Δ and it was obtained from ⊩_mΓ,¬χ ⇒ ϕ,Δ and ⊩_nΓ,¬χ ⇒ ψ,Δ. By Lemma B.1 we have either $\vdash _{\leq j-1}{\Gamma }\nRightarrow \chi , \phi , {\Delta }$ or $\vdash _{\leq j-1}{\Gamma }\nRightarrow \chi , \psi , {\Delta }$. Let’s assume, without loss of generality, that the former holds. Then we can apply L¬⁻ to obtain $\vdash _{\leq j}{\Gamma }\neg \chi \nRightarrow \phi , {\Delta }$. Once more, there is an external inconsistency and the combined rank has been reduced.

    

  • If ${\Gamma }\nRightarrow \phi \wedge \psi , {\Delta }$ was obtained by an application of LV al⁻, then we have both ⊩_iΓ,V al(〈Φ〉,〈Ψ〉) ⇒ ϕ ∧ ψ,Δ and $\vdash _{j}{\Gamma }, Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\nRightarrow \phi \wedge \psi , {\Delta }$. The former was obtained from ⊩_mΓ,V al(〈Φ〉,〈Ψ〉) ⇒ ϕ,Δ and ⊩_nΓ,V al(〈Φ〉,〈Ψ〉) ⇒ ψ,Δ. The latter from the sequent ⊩_kΦ ⇒Ψ and the anti-sequent $\vdash _{l}{\Gamma }\nRightarrow \phi \wedge \psi , {\Delta }$, where m + n + 1 = i and k + l + 1 = j. By Lemma B.1, we also have either $\vdash _{\leq l}{\Gamma }\nRightarrow \phi , {\Delta }$ or $\vdash _{\leq l}{\Gamma }\nRightarrow \psi , {\Delta }$. Let’s assume, once more without loss of generality, that the former holds. Then, an application of LV al⁻ delivers $\vdash _{\leq j}{\Gamma }, Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\nRightarrow \phi , {\Delta }$. Thus, we have an external inconsistency and the combined rank has been reduced.

    

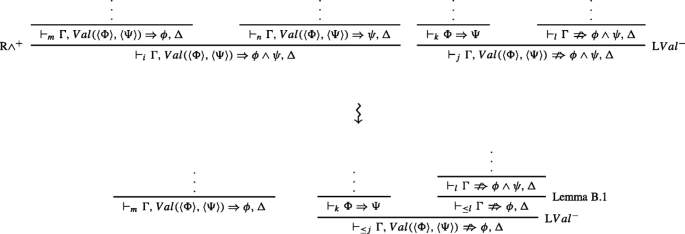
• Lastly, we need to take care of the validity rules. There are three cases to consider: (i) the sequent Γ ⇒Δ is of the form Γ ⇒ V al(〈Φ〉,〈Ψ〉),Δ and was obtained from Γ,Φ ⇒Ψ,Δ by an application of RV al⁺, (ii) the sequent Γ ⇒Δ is of the form V al(〈Φ〉,〈Ψ〉) ⇒ and comes from ${\Phi }\nRightarrow {\Psi }$ by an application of LV al⁺, and (iii) the sequent Γ ⇒Δ is of the form V al(〈Φ〉,〈Ψ〉),Φ ⇒Ψ and is an instance of V D⁺. Case (i) is very similar to the logical rules and presents no difficulties, so I will only consider cases (ii) and (iii).

  • If the sequent Γ ⇒Δ is of the form ⊩_iV al(〈Φ〉,〈Ψ〉) ⇒ and was obtained from $\vdash _{i-1}{\Phi }\nRightarrow {\Psi }$ by an application of LV al⁺, then the corresponding anti-sequent is $\vdash _{j} Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\nRightarrow$. But this could only have been obtained from ⊩_nΦ ⇒Ψ and $\vdash _{1}\nRightarrow$ by an application of LV al⁻, where n + 2 = j. So, we have an external inconsistency and the combined rank has been reduced.

  • If the sequent Γ ⇒Δ is an instance of V D⁺, it is of the form ⊩₁V al(〈Φ〉,〈Ψ〉),Φ ⇒Ψ. Then the corresponding anti-sequent is $\vdash _{j} Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle ), {\Phi }\nRightarrow {\Psi }$. But, by Lemma B.2, LV al⁻ is rank-preserving invertible, and this means that there are derivations of both ⊩_nΦ ⇒Ψ and $\vdash _{m}{\Phi }\nRightarrow {\Psi }$, where n + m ≤ j. So, we can reach an external inconsistency and the combined rank has been reduced.

    

□

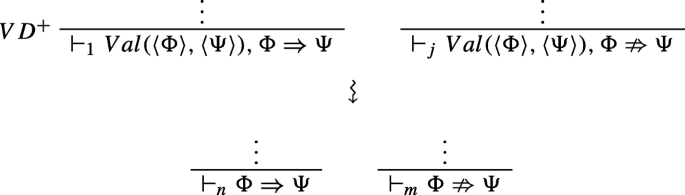
It is interesting to note three things. First, the last case in this proof crucially uses the notion of rank, rather than the notion of height. There is no guarantee that the (combined) height has been reduced, since the height of Φ ⇒Ψ plus the height of ${\Phi }\nRightarrow {\Psi }$ (n + m) could be greater than the height of $\vdash _{k} Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle ), {\Phi }\nRightarrow {\Psi }$, which is max(n,m) + 1.

Second, the proof deals with rules and not with types of statements. So self-referential statements, like π, need no special treatment. In fact, the proof holds regardless of the choice of the denotation function f. Whatever statement one considers, self-referential or not, it will be either a propositional variable, a negation, a conjunction, or a validity claim. This statement will be part of a sequent or an anti-sequent, and that sequent or anti-sequent must be either an axiom, an anti-axiom, or it must have been obtained by one of the rules. Given that all these cases are covered, the proof is compatible with denotation functions f allowing for all sorts of self-referential statements.

Third, as I mentioned in Appendix A, the proof of External Consistency resembles typical proofs that the rule of cut is eliminable. The only novelty is that, due to the presence of anti-sequents, the proof has to be by induction on the “combined rank”. External Completeness, however, is another thing entirely. Its proof is not like a cut-elimination proof at all. If anything, it resembles completeness proofs for sequent calculi. The difference is that instead of taking an open branch and providing instructions for how to construct a countermodel of the sequent (anti-sequent) that is the root of that branch, one provides instructions for how to transform the open branch into a derivation of the corresponding anti-sequent (sequent).

As a corollary of Theorem B.3 we know that:

Theorem B.4 (External consistency of ${\mathscr{H}}^{V}_{{\mathscr{L}}}$)

${\mathscr{H}}^{V}_{{\mathscr{L}}}$ is externally consistent.

Proof

Every derivation of ${\mathscr{H}}^{V}_{{\mathscr{L}}}$ is also a derivation of ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$. So, if ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$ is externally consistent, so is ${\mathscr{H}}^{V}_{{\mathscr{L}}}$. □

Appendix C: Summary of Acronyms and Abbreviations

The paper contains a lot of acronyms and abbreviations, so below I provide a list of them for easy reference:

• VD is the rule of validity detachment, which states that ψ follows from ϕ and V al(〈ϕ〉,〈ψ〉).

• VP stands for the rule of validity proof, according to which if ψ follows from ϕ, then V al(ϕ,ψ) has a derivation.

• π is an abbreviation for the statement V al(〈π〉,〈⊥〉).

• VAL stands for the condition that an argument from Γ to ϕ is ⊩-valid if and only if ⊩ proves the statement expressing that the argument from Γ to ϕ is valid.

• INV stands for the condition that the argument from Γ to ϕ is ⊩-invalid if and only if ⊩ disproves the statement expressing that the argument from Γ to ϕ is valid.

• ${\mathscr{H}}$ is the purely logical hybrid system.

  • Its structural rules are Identity, ID⁺, Anti-Identity, ID⁻, Weakening, W⁺, and Anti-Weakening, W⁻.

  • Its operational rules for ⊥, ¬ and ∧ are L⊥⁺, R⊥⁻, L¬⁺, R¬⁺, L¬⁻, R¬⁻, L∧⁺, R∧⁺, L∧⁻, and R∧⁻.

• RV al⁺ is the rule licensing the step from Γ,Φ ⇒Ψ,Δ to Γ ⇒ V al(〈Φ〉,〈Ψ〉),Δ.

• LV al⁺ is the (hybrid) rule licensing the step from ${\Phi }\nRightarrow {\Psi }$ to V al(〈Φ〉,〈Ψ〉) ⇒.

• LV al⁻ is the (hybrid) rule licensing the step from Φ ⇒Ψ and ${\Gamma }\nRightarrow {\Delta }$ to ${\Gamma }, Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\nRightarrow {\Delta }$.

• RV al⁻ is the rule licensing the step from ${\Gamma }, {\Phi }\nRightarrow {\Psi }, {\Delta }$ to ${\Gamma }\nRightarrow Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle ), {\Delta }$.

• ${\mathscr{H}}^{V}_{{\mathscr{L}}}$ is the result of adding the rules RV al⁺, LV al⁺, LV al⁻ and RV al⁻ to ${\mathscr{H}}$.

• F-VAL is a formal counterpart of VAL stating that Φ ⇒Ψ has a derivation if and only if ⇒ V al(〈Φ〉,〈Ψ〉) has a derivation.

• F-INV is a formal counterpart of INV stating that ${\Phi }\nRightarrow {\Psi }$ has a derivation if and only if V al(〈Φ〉,〈Ψ〉) ⇒ has a derivation.

• F-VAL^∗ is a variant of F-VAL according to which Φ ⇒Ψ has a derivation if and only if $Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )\nRightarrow$ has a derivation.

• F-INV^∗ is a variant of F-INV according to which ${\Phi }\nRightarrow {\Psi }$ has a derivation if and only if $\nRightarrow Val(\langle {\Phi }\rangle , \langle {\Psi }\rangle )$ has a derivation.

• ${\mathscr{H}}^{V}_{\circlearrowleft }$ is exactly as ${\mathscr{H}}^{V}_{{\mathscr{L}}}$ but is couched in a language that contains self-referential statements.

• ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$ is exactly as ${\mathscr{H}}^{V}_{\circlearrowleft }$ except that it contains the rule V D⁺, which is a generalization of VD to multisets.

• LW⁺ and RW⁺ are the standard (positive) contraction rules.

• LW⁻ and RW⁻ are the anti-contraction rules.

• $\mathcal {W}{\mathscr{H}}^{V^{+}}_{\circlearrowleft }$ is exactly as ${\mathscr{H}}^{V^{+}}_{\circlearrowleft }$ except that it contains the contraction and anti-contraction rules LW⁺, RW⁺, LW⁻ and RW⁻.