Abstract
The transition semantics presented in Rumberg (J Log Lang Inf 25(1):77–108, 2016a) constitutes a fine-grained framework for modeling the interrelation of modality and time in branching time structures. In that framework, sentences of the transition language \(\mathcal {L}_\mathsf{t}\) are evaluated on transition structures at pairs consisting of a moment and a set of transitions. In this paper, we provide a class of first-order definable Kripke structures that preserves \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. transition structures. As a consequence, for a certain fragment of \(\mathcal {L}_\mathsf{t}\), validity w.r.t. transition structures turns out to be axiomatizable. The result is then extended to the entire language \(\mathcal {L}_\mathsf{t}\) by means of a quite natural ‘Henkin move’, i.e. by relaxing the notion of validity to bundled structures.
Similar content being viewed by others
1 Introduction
The Prior-Thomason theory of branching time provides a perspicuous representation of the idea that the past is fixed while the future may be open. In a branching time structure, the interrelation of modality and time is depicted as a tree of moments that branches toward the future (cf. Prior 1967; Thomason 1970). At any given moment, there may be alternative possibilities for the future, and which of the alternative future possibilities will be realized depends on how the future unfolds.
Branching time structures allow for different parameters of truth, resulting in different descriptions of the interrelation of modality and time. There are two traditional semantic approaches to branching time, which Prior (1967) refers to as Peirceanism and Ockhamism. While Peirceanism makes use of a moment parameter only, in the Ockhamist semantics, truth at a moment is relativized to a history, which represents a complete possible course of events. The distinctive feature of the transition semantics presented in Rumberg (2016a) is that it builds on local future possibilities, viz. transitions, rather than on histories. Possible courses of events are modeled by sets of transitions, where each transition specifies an immediate possible future continuation at a branching point. As a consequence, incomplete possible courses of events become available as well, which can then be extended toward the future. The Ockhamist history parameter is replaced by a dynamic transition parameter. In addition to modal and temporal operators, the transition language \(\mathcal {L}_\mathsf{t}\) is equipped with a stability operator \(\mathsf {S}\), which is interpreted as a universal quantifier over the possible future extensions of a given transition set and brings to the fore the idea that contingencies about the future dissolve as time progresses. The semantics on transition structures developed along those lines enables a fine-grained picture of the interrelation of modality and time and comprises both Peirceanism and Ockhamism as limiting cases, exceeding both accounts in terms of expressive strength.
In this paper, we establish axiomatizability results for the transition framework by showing that transition structures are first-order definable. Axiomatizations of branching time logics are an intricate issue. Complications arise, first and foremost, from the fact that branching time logics may involve higher-order quantification over possible courses of events (cf. Zanardo 2006b). The literature on branching time offers several results on the axiomatizability of Peirceanism and Ockhamism, whose Priorean semantics makes use of second-order quantification over histories. In Burgess (1980), Peirceanism is proven to be axiomatizable and a finite axiomatization is provided.Footnote 1 The proof rests on a so-called ‘Henkin move’: branching time structures are endowed with a primitive set of histories, a so-called bundle; and it is shown that, in the Peircean case, validity w.r.t. bundled trees coincides with validity w.r.t. branching time structures. When it comes to Ockhamism, the situation is more complex: in the Ockhamist semantics, histories are employed as a second parameter of truth, which creates the need to unravel the structure between the indices of evaluation. The resulting Ockhamist frames are first-order definable Kripke structures with a genuine Kripe-style semantics that preserve Ockhamist validity w.r.t. bundled trees (cf. Zanardo 1985, 1996), which is strictly weaker than Ockhamist validity w.r.t. branching time structures (cf. Burgess 1978; Reynolds 2002). It follows that Ockhamist validity w.r.t. bundled trees is axiomatizable. A finite axiomatization of Ockhamist bundled tree validity is given in Zanardo (1985). Finding a complete axiomatization of Ockhamist validity w.r.t. branching time structures, which is known to be axiomatizable as well (cf. Burgess 1979; Gurevich and Shelah 1985), seems still an open problem.
The result we establish in the present paper parallels the Peircean and the Ockhamist cases in a certain respect. Just as Ockhamism, the transition semantics is not a genuine Kripke-style semantics: the semantics makes use of a second parameter of truth next to the moment parameter, and the language \(\mathcal {L}_\mathsf{t}\) is equipped with intensional operators that are interpreted as quantifiers over that second parameter. The crucial difference with Ockhamism then consists in the fact that, in the transition semantics, the structural elements that are employed as a second parameter of truth are sets of transitions rather than histories; histories play only a secondary, Peircean-like role. Sets of transitions are set-theoretically rather complex, however, much more complex than histories: they are sets of pairs whose second component is a set of histories. In this paper, we provide a class of genuine Kripke structures that preserves \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. transition structures, viz. the class of so-called index structures. They are the transition-theoretic analogue of Ockhamist frames. One merit of index structures is that they evade the set-theoretic complexity of transition sets. In fact, index structures are first-order definable, which then naturally leads to axiomatizability results.
Our definition of an index structure draws on the fact that transition sets correspond one-to-one to certain substructures of branching time structures, which we call prunings. The first-order definability of index structures is essentially a result of that correspondence: the prunings of a given branching time structure are first-order definable substructures. In index structures, the semantics of all but one of the intensional operators of the transition language \(\mathcal {L}_\mathsf{t}\) dissolves into first-order quantification over the points of the structure in accordance with the respective accessibility relations. The only exception is given by the strong future operator \({\mathsf{F}}\), whose index semantics is a Peircean-like semantics that involves second-order quantification over histories. Then, since index structures are first-order definable, validity of \({\mathsf{F}}\)-free \(\mathcal {L}_\mathsf{t}\)-formulas w.r.t. transition structures is axiomatizable.
Similar to the Peircean case, the complication arising from the strong future operator can be dealt with by means of a quite natural ‘Henkin move’, i.e. by relaxing the notion of validity to bundled structures. Both transition structures and index structure are endowed with a primitive set of histories, or a so-called bundle. We show that bundled index structures are again first-order definable and that \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. bundled transition structures is equivalent to \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. bundled index structures. As a consequence, \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. bundled transition structures turns out to be axiomatizable.
The paper is structured as follows: in Sect. 2, we introduce the framework of branching time and provide a brief overview of the transition semantics presented in Rumberg (2016a). In Sect. 3, we establish a bijective correspondence between transition sets and prunings. On the basis of that result, in Sect. 4, we then put forth our definition of the notion of an index structure, and, in Sect. 5, we show that there is a one-to-one correspondence up to isomorphism between index structures and transition structures that preserves \(\mathcal {L}_\mathsf{t}\)-validity. Section 6 is devoted to a proof of the first-order definability of index structures and its implications with regard to axiomatizability. Finally, in Sect. 7, we deal with the complication posed by the strong future operator \({\mathsf{F}}\) and generalize the results of Sects. 5 and 6 to bundled structures.
2 Preliminaries
In this section, we introduce the Prior-Thomason theory of branching time and review the core ideas of the transition semantics. For a detailed discussion of the transition framework and its philosophical motivation, we refer the reader to Rumberg (2016a).
As said, in the theory of branching time, the modal-temporal structure of the world is represented as a tree of moments that branches toward the future. Formally, a branching time structure (or short: BT structure) is defined as a non-empty strict partial ordering of moments \(\mathcal {M}=\langle M,<\rangle \) that is (BT1) left-linear, (BT2) jointed and (BT3) serial. Every maximal <-linear set of moments in M is called a history.
Definition 1
(BT structure) A BT structure\(\mathcal {M}=\langle M,<\rangle \) is a non-empty strict partial order (i.e. a set \(M \ne \emptyset \) together with a relation < that is irreflexive, asymmetric and transitive) s.t.
-
(BT1)
for all \(m,m',m'' \in M\), if \(m'<m\) and \(m''<m\), then \(m'\le m''\) or \(m''\le m'\) (left-linearity);
-
(BT2)
for all \(m',m'' \in M\), there is some \(m\in M\) s.t. \(m\le m'\), \(m \le m''\) and for all \(m_0 \in M\), if \(m_0 \le m'\) and \(m_0\le m''\), then \(m_0\le m\) (jointedness);Footnote 2
-
(BT3)
for all \(m \in M\), there is some \(m'\in M\) s.t. \(m<m'\) (seriality).
Definition 2
(History) Given a BT structure \(\mathcal {M}=\langle M,<\rangle \), a set \(h \subseteq M\) is a history iff h is a maximal <-linear subset of M. Let \({\mathsf{hist}}(\mathcal {M})\) be the set of histories in\(\mathcal {M}\). For a moment \(m \in M\), the set of histories containingm is denoted by \(\mathsf {H}_m\); so \(\mathsf {H}_m:= \{h \in {\mathsf{hist}}(\mathcal {M})\mid m \in h\}\).
Transitions provide a local alternative to histories: whereas histories represent complete possible courses of events, a transition specifies one of the alternative immediate future possibilities open at a branching point. The definition of a transition is based on the relation of undividedness, which captures the local branching behavior of histories at a given moment.
Definition 3
(Undividedness and Branching) Given a BT structure \(\mathcal {M}=\langle M,<\rangle \) and a moment \(m\in M\), two histories \(h,h'\in {\mathsf{hist}}(\mathcal {M})\) are undivided-at-m, in symbols: \(h\equiv _m h'\), iff there is some \(m'\in h\cap h'\) s.t. \(m'>m\). In case \(m \in M\) is the greatest element in \(h\cap h'\), we say that h and \(h'\)branch atm(in\(\mathcal {M}\)), in symbols: \(h\perp _m h'\) (in \(\mathcal {M}\)), and we call the moment m a branching point.
Conditions (BT1) and (BT2) of Definition 1 jointly ensure that any two distinct histories branch at some moment. Also observe that \(h\perp _m h'\) implies \(h\not = h'\). We can then extend the notation \(h\perp _m h'\) to moments in a natural way: we write \(m' \perp _m m''\) (in \(\mathcal {M}\)) to indicate that \(m'>m<m''\) is a branching triangle in\(\mathcal {M}\), i.e. \(m'\) and \(m''\) are <-incomparable and m is their greatest common lower <-bound in \(\mathcal {M}\).
For any moment \(m\in M\), the relation of undividedness-at-m is an equivalence relation on the set \(\mathsf {H}_m\) of histories containing m and hence yields a partition of that set. We denote the \(\equiv _m\)-equivalence class of a history \(h\in \mathsf {H}_m\) by \([h]_m\). Note that the relation of undividedness is downward entailing: any two histories that are undivided at some moment m, are undivided at any moment \(m'<m\). In particular, for all \(h\in \mathsf {H}_m\), \(m'<m\) implies \(\mathsf {H}_m\subseteq [h]_{m'}\).
A transition is defined as an initial-outcome pair \(\langle m\!\rightarrowtail \!H\rangle \) consisting of a branching point \(m\in M\) and an equivalence class \(H\in \mathsf {H}_m/\!\equiv _m\).
Definition 4
(Transition) For \(\mathcal {M}=\langle M,<\rangle \) a BT structure, a transition is a pair \(\langle m,H\rangle \), also written \(\langle m\!\rightarrowtail \!H\rangle \), where \(m\in M\) is a branching point and \(H\in \mathsf {H}_m/\!\equiv _m\). Let \({\mathsf{trans}\;}(\mathcal {M})\) be the set of all transitions in\(\mathcal {M}\).
Sets of transitions provide a perspicuous means to represent possible courses of events in a branching time structure, as indicated in Fig. 1. We can define a natural ordering \(\prec \) between the transitions in \({\mathsf{trans}\;}(\mathcal {M})\) in terms of proper set inclusion on the outcomes. Note that \([h]_{m} \subsetneq [h]_{m'}\) implies \(m'<m\).
Definition 5
(Transition ordering) Given a BT structure \(\mathcal {M}=\langle M,<\rangle \) and transitions \(\langle m\!\rightarrowtail \!H\rangle , \langle m'\!\rightarrowtail \!H'\rangle \in {\mathsf{trans}\;}(\mathcal {M})\), we say that \(\langle m'\!\rightarrowtail \!H'\rangle \)precedes\(\langle m\!\rightarrowtail \!H\rangle \), in symbols: \(\langle m'\!\rightarrowtail \!H'\rangle \prec \langle m\!\rightarrowtail \!H\rangle \), iff \(H\subsetneq H'\).
Every downward closed \(\prec \)-chain of transitions represents a possible course of events, a complete or an initial partial one. It allows certain histories to occur while it may excludes others. The set of histories allowed by a transition set is thereby nothing but the intersection over the outcomes of those transitions. There are two limiting cases: on the one hand, there is the empty set of transitions, which allows any history in \(\mathcal {M}\) to occur; on the other hand, there are maximal \(\prec \)-linear sets of transitions, each of which excludes all but a single history. A set of transitions is called consistent iff it allows at least one history to occur. In Rumberg (2016a, Prop. 1) it is shown that consistency is equivalent to the requirement that the transition set be linearly ordered via \(\prec \).
Definition 6
(The set of histories allowed by T) Given a BT structure \(\mathcal {M}=\langle M,<\rangle \) and a (possibly empty) set of transitions \(T\subseteq {\mathsf{trans}\;}(\mathcal {M})\), the set of histories allowed byT is given by
Definition 7
(Consistency) For \(\mathcal {M}=\langle M,<\rangle \) a BT structure, a transition set \(T\subseteq {\mathsf{trans}\;}(\mathcal {M})\) is consistent iff \({\mathsf{H}}(T)\ne \emptyset \).
Given a BT structure \(\mathcal {M}\), the set of all consistent, \(\prec \)-downward closed transition sets in \(\mathcal {M}\) is denoted by \({\mathsf{dcts}}(\mathcal {M})\).
Definition 8
(The set\(\mathsf {dcts}\)) For \(\mathcal {M}=\langle M,<\rangle \) a BT structure, the set of consistent,\(\prec \)-downward closed sets of transitions in\(\mathcal {M}\) is given by:
As a possibly non-maximal \(\prec \)-chain that is closed toward the past, every transition set \(T\in {{{{\mathsf{dcts}}(\mathcal {M})}}}\) uniquely specifies a possible course of events that stretches linearly all the way from the past toward a possibly open future. We show that for all \(T\in {\mathsf{dcts}}(\mathcal {M})\), the correspondence \(T \mapsto {\mathsf{H}}(T)\) is injective and reverses the inclusion relation.Footnote 3
Lemma 1
Let \(\mathcal {M}=\langle M,<\rangle \) be a BT structure. For all \(T,T'\in {{\mathsf{dcts}}(\mathcal {M})}\), we have \(T=T'\) iff \({\mathsf{H}}(T)= {\mathsf{H}}(T')\). In particular, \(T\subsetneq T'\) iff \({\mathsf{H}}(T')\subsetneq {\mathsf{H}}(T)\).
Proof
Obviously, \(T=T'\) implies \({\mathsf{H}}(T)=\mathsf {H}(T')\). We prove that the converse holds as well. Assume that \(T\ne T'\) with \(\langle m'\!\rightarrowtail \!H'\rangle \in T'\setminus T\). Two cases can be considered. Case (i): Assume that \(T \subsetneq T'\). Then for all \(\langle m\!\rightarrowtail \!H\rangle \in T\), \(\langle m\!\rightarrowtail \!H\rangle \prec \langle m'\!\rightarrowtail \!H'\rangle \), which implies \(\mathsf {H}_{m'}\subseteq {\mathsf{H}}(T)\). Since \(\mathsf {H}(T')\subseteq H' \subsetneq \mathsf {H}_{m'}\), it follows that \(\mathsf {H}(T')\subsetneq {\mathsf{H}}(T)\). Case (ii): Assume that \(T \not \subseteq T'\). Then there is some \(\langle m\!\rightarrowtail \!H\rangle \in T\setminus T'\), and we have \(H\not \subseteq H'\) and \(H'\not \subseteq H\). Let \(h\in H\setminus H'\) and \(h'\in H'\setminus H\), and assume \(h \perp _{m''} h'\). Then \(m \ge m'' \le m'\). Consequently, \(\langle m''\!\rightarrowtail \! [h]_{m''}\rangle \in T\) and \(\langle m''\!\rightarrowtail \! [h']_{m''}\rangle \in T'\), from which it follows that \({\mathsf{H}}(T)\cap \mathsf {H}(T')=\emptyset \) and hence \({\mathsf{H}}(T)\ne \mathsf {H}(T')\).
We finally show that \(\mathsf {H}(T')\subsetneq {\mathsf{H}}(T)\) implies \(T\subsetneq T'\), having established the converse implication in case (i) above. Assume \(h\in {\mathsf{H}}(T)\setminus \mathsf {H}(T')\), let \(h'\in \mathsf {H}(T')\), and suppose \(h\perp _m h'\). Then there is some \(\langle m'\!\rightarrowtail \!H'\rangle \in T'\) s.t. \(h'\in H'\) but \(h \notin H'\). The latter requires \(m'\ge m\). But then, since \({\mathsf{H}}(T)\supseteq \{h,h'\}\), \(T \subseteq \{\langle m''\!\rightarrowtail \!H''\rangle \in {\mathsf{trans}\;}(\mathcal {M})\mid m''<m \text { and } h'\in H''\} \subsetneq T'\). \(\square \)
The transition semantics, in its most general form, is based on transition structures. A transition structure is a BT structure \(\mathcal {M}\) together with a non-empty set of transition sets \({\textit{ts}}\subseteq {\mathsf{dcts}}(\mathcal {M})\) that covers the entire BT structure.
Definition 9
(Transition structure) A transition structure is a triple \(\mathcal {M}^{\textit{ts}}= \langle M,<,{\textit{ts}}\rangle \) where \(\mathcal {M}=\langle M,<\rangle \) is a BT structure and \({\textit{ts}}\subseteq {\mathsf{dcts}}(\mathcal {M})\) a non-empty set of transition sets s.t. for every \(m\in M\), there is some \(T\in {\textit{ts}}\) s.t. \({\mathsf{H}}(T)\cap \mathsf {H}_m\ne \emptyset \).
Transition structures allow for great generality. Both Peirceanism and Ockhamism can be viewed as restrictions on the class of transition structures: restricting the set \({\textit{ts}}\) to the empty transition set yields Peirceanism, while a restriction to all maximal \(\prec \)-linear transition sets yields Ockhamism (cf. Rumberg 2016a, Sect. 4). The definition of a transition structure involves a so-called ‘Henkin move’, a standard technique in branching time logics.Footnote 4 In Sect. 7, we will perform a second ‘Henkin move’: transition structures will be endowed with a primitive set of histories.
The language \(\mathcal {L}_\mathsf{t}\) of the transition semantics extends the standard propositional language \(\mathcal {L}\) (with propositional variables and the usual Boolean connectives) by a past operator, \(\mathsf {P}\), a weak and a strong future operator, \(\mathsf {f}\) and \({\mathsf{F}}\), an inevitability operator \(\Box \) and a stability operator \(\mathsf {S}\). The stability operator is specific to the transition approach, which allows for the relativization to incomplete possible courses of events. In the transition semantics, the truth value of a sentence at a moment can change if the transition set is extended so that it stretches further into the future. As a universal quantifier over the possible future extensions of a given transition set, the stability operator enables us to capture the peculiar behavior of the truth value of a sentence at a moment in the course of time: its changing from contingent to stably-true or stably-false. The stability operator gains its significance in the context of future contingents, whose truth values only stabilize as the future unfolds.
Sentences of \(\mathcal {L}_\mathsf{t}\) are evaluated on a transition structure \(\mathcal {M}^{\textit{ts}}=\langle M,<,{\textit{ts}}\rangle \) at pairs m / T, where \(m\in M\), \(T\in {\textit{ts}}\) and \({\mathsf{H}}(T)\cap \mathsf {H}_m\ne \emptyset \). Given a transition structure \(\mathcal {M}^{\textit{ts}}\), we denote the set of indices of evaluation by \({\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\).
Definition 10
(Transition model) A transition model is a quadruple \({\mathfrak {M}}^{\textit{ts}}=\langle M,<,{\textit{ts}},v_\mathsf {t}\rangle \) where \(\mathcal {M}^{\textit{ts}}=\langle M,<,{\textit{ts}}\rangle \) is a transition structure and  a valuation function.
a valuation function.
The following semantic clauses extend the valuation \(v_\mathsf {t}\) on the propositional variables \(p\in \mathsf {At}\) in a transition model \({\mathfrak {M}}^{\textit{ts}}\) to any arbitrary sentence \(\phi \in \mathcal {L}_\mathsf{t}\):
- (\(\mathsf {At}\)):
-
\({\mathfrak {M}}^{\textit{ts}}\!,m/T\vDash _\mathsf{t}p\) iff \(v_\mathsf {t}(p,m/T)=1\);
- (\(\lnot \)):
-
\({\mathfrak {M}}^{\textit{ts}}\!,m/T\vDash _\mathsf{t}\lnot \phi \) iff \({\mathfrak {M}}^{\textit{ts}}\!,m/T\not \vDash _\mathsf{t}\phi \);
- (\(\wedge \)):
-
\({\mathfrak {M}}^{\textit{ts}}\!,m/T\vDash _\mathsf{t}\phi \wedge \psi \) iff \({\mathfrak {M}}^{\textit{ts}}\!,m/T\vDash _\mathsf{t}\phi \) and \({\mathfrak {M}}^{\textit{ts}}\!,m/T\vDash _\mathsf{t}\psi \);
- (\(\mathsf {P}\)):
-
\({\mathfrak {M}}^{\textit{ts}}\!,m/T\vDash _\mathsf{t}\mathsf {P}\phi \) iff there is some \(m'<m\) s.t. \({\mathfrak {M}}^{\textit{ts}}\!,m'/T\vDash _\mathsf{t}\phi \);
- (\(\mathsf {f}\)):
-
\({\mathfrak {M}}^{\textit{ts}}\!,m/T\vDash _\mathsf{t}\mathsf {f}\phi \) iff there is some \(m'>m\) s.t. \({\mathsf{H}}(T)\cap \mathsf {H}_{m'}\ne \emptyset \) and \({\mathfrak {M}}^{\textit{ts}}\!,m'/T\vDash _\mathsf{t}\phi \);
- (\({\mathsf{F}}\)):
-
\({\mathfrak {M}}^{\textit{ts}}\!,m/T\vDash _\mathsf{t}{\mathsf{F}}\phi \) iff for all \(h\in {\mathsf{H}}(T)\cap \mathsf {H}_m\), there is some \(m'\in h\) s.t. \(m'>m\) and \({\mathfrak {M}}^{\textit{ts}}\!,m'/T\vDash _\mathsf{t}\phi \);
- (\(\Box \)):
-
\({\mathfrak {M}}^{\textit{ts}}\!,m/T\vDash _\mathsf{t}\Box \phi \) iff for all \(T'\in {\textit{ts}}\) s.t. \(\mathsf {H}(T')\cap \mathsf {H}_m\ne \emptyset \), \({\mathfrak {M}}^{\textit{ts}}\!,m/T'\vDash _\mathsf{t}\phi \);
- (\(\mathsf {S}\)):
-
\({\mathfrak {M}}^{\textit{ts}}\!,m/T\vDash _\mathsf{t}\mathsf {S}\phi \) iff for all \(T'\in {\textit{ts}}\) s.t. \(T'\supseteq T\) and \(\mathsf {H}(T')\cap \mathsf {H}_m\ne \emptyset \), \({\mathfrak {M}}^{\textit{ts}}\!, m/T'\vDash _\mathsf{t}\phi \).
3 Transition Sets and Prunings
The transition sets that are employed as a second parameter of truth in the transition semantics are set-theoretically rather complex. From a logical point of view, however, a set of transitions is nothing over and above the set of histories it admits. In this section, we show that sets of transitions correspond one-to-one to certain substructures of BT structures, which we call prunings. In a nutshell, a pruning of a given BT structure is a substructure of the latter that is obtained by cutting out certain branches, namely all those branches that are excluded by the corresponding transition set.Footnote 5
A pruning of a BT structure \(\mathcal {M}=\langle M,<\rangle \) is a substructure \(\mathcal {M}' \subseteq \mathcal {M}\) that (i) shares at least one history with \(\mathcal {M}\) and is such that (ii) if it contains two <-incomparable moments, it contains all moments in the past and future of their greatest common lower <-bound in M as well. For any moment \(m\in M\), we denote the set \(\{m'\in M\mid m'\le m \text { or } m'>m\}\) by \(M_m\).
Definition 11
(Pruning) Given a BT structure \(\mathcal {M}=\langle M,<\rangle \), a pruning of \(\mathcal {M}\) is a substructure \(\mathcal {M}'=\langle M',<\!\vert _{M'}\rangle \) of \(\mathcal {M}\) s.t.
-
(i)
\({\mathsf{hist}}(\mathcal {M})\cap {\mathsf{hist}}(\mathcal {M}')\ne \emptyset \);
-
(ii)
for all \(m \in M\) and \(m',m'' \in M'\), if \(m' \perp _m m''\), then \(M_m\subseteq M'\).
Let \({\mathsf{prun}}(\mathcal {M})\) be the set of all prunings of \(\mathcal {M}\).
In the sequel, whenever \(X'\subseteq X\) and R is an order relation on X, we use \(\langle X',R\rangle \) as an abbreviation for \(\langle X',R\vert _{X'}\rangle \). The substructure \(\mathcal {M}'\subseteq \mathcal {M}\) in the previous definition, for instance, will then be written \(\langle M',<\rangle \).
Note that condition (i) of Definition 11, as stated above, is a second-order condition as it implicitly involves quantification over histories. The condition is triggered by the need to cover the case in which \(\mathcal {M}'\) consists of just a single history. There is no need, however, to formulate the condition as a second-order condition. Since the first condition is implied by the second one whenever \(\mathcal {M}'\) comprises more than one history, we can replace clause (i) in Definition 11 by the following condition without loss of generality:
- (i’):
-
if \(M'\) is a <-linear subset of M, then \(M'\) is <-downward closed in M and there is no \(m\in M\) s.t. for all \(m'\in M'\), \(m'< m\).
Conditions (i) [resp. (i’)] and (ii) of Definition 11 jointly ensure that every pruning \(\mathcal {M}'\) of a BT structure \(\mathcal {M}\) is spanned by a non-empty set of histories in \(\mathcal {M}\). As a consequence, prunings are themselves BT structures.
Lemma 2
Let \(\mathcal {M}=\langle M,<\rangle \) be a BT structure, and let \(\mathcal {M}'=\langle M',<\rangle \) be a pruning of \(\mathcal {M}\). Then \({{{{\mathsf{hist}}(\mathcal {M}')}}} \subseteq {{{{\mathsf{hist}}(\mathcal {M})}}}\).
Proof
Straightforward by Definition 11. \(\square \)
Even though it is not the case in general that the intersection \(\bigcap {\mathsf{hist}}(\mathcal {M})\) of all histories in a BT structure \(\mathcal {M}\) is non-empty, for every proper pruning \(\mathcal {M}'\) of \(\mathcal {M}\), we have \(\bigcap {\mathsf{hist}}(\mathcal {M}')\ne \emptyset \). This is due to the fact that, by Definition 11, all histories in \(\mathcal {M}'\) need to be undivided at every moment at which a branch has dropped off (cf. Lemma 3). Given a BT structure \(\mathcal {M}\), we call the (possibly empty) intersection \(\bigcap {\mathsf{hist}}(\mathcal {M})\) the trunk of \(\mathcal {M}\), and we denote it by \(\mathsf {Trunk}(\mathcal {M})\).
Lemma 3
Let \(\mathcal {M}=\langle M,<\rangle \) be a BT structure, and let \(\mathcal {M}'=\langle M',<\rangle \) be a proper pruning of \(\mathcal {M}\). Let \(h\in {{{{\mathsf{hist}}(\mathcal {M})}}}\setminus {{{{\mathsf{hist}}(\mathcal {M}')}}}\), \(h'\in {{{{\mathsf{hist}}(\mathcal {M}')}}}\) and assume \(h \perp _m h'\) in \(\mathcal {M}\). Then \({{{{\mathsf{hist}}(\mathcal {M}')}}} \subseteq [h']_m\).
Proof
Under the given assumptions, we can consider some \(m'\in h\setminus M'\) s.t. \(m<m'\). Assume for reductio that there is some \(h''\in {\mathsf{hist}}(\mathcal {M}')\setminus [h']_m\). This implies that there is some \(m''\in M\) s.t. \(m''\le m\) and \(h'\perp _{m''} h''\). By Definition 11 (ii) we then have \(M_{m''} \subseteq M'\). Since \(m''\le m<m'\), it follows that \(m'\in M'\), which contradicts the assumption that \(m'\in h\setminus M'\). \(\square \)
It is readily verified that the pruning relation between BT structures is reflexive, antisymmetric and transitive, i.e. a partial order. When restricted to the set \({\mathsf{prun}}(\mathcal {M})\) of prunings of a given BT structure \(\mathcal {M}\), the pruning relation coincides with the substructure relation.
Lemma 4
Let \(\mathcal {M}=\langle M,<\rangle \) be a BT structure, and let \(\mathcal {M}'=\langle M',<\rangle \) and \(\mathcal {M}''=\langle M'',<\rangle \) be prunings of \(\mathcal {M}\). If \(\mathcal {M}''\subseteq \mathcal {M}'\), then \(\mathcal {M}''\) is a pruning of \(\mathcal {M}'\).Footnote 6
Proof
Assume that \(\mathcal {M}',\mathcal {M}''\in {\mathsf{prun}}(\mathcal {M})\) with \(\mathcal {M}''\subseteq \mathcal {M}'\). Condition (i) of Definition 11 is trivially fulfilled by \(\mathcal {M}'\) and \(\mathcal {M}''\): by Lemma 2, every \(h\in \mathsf {hist}(\mathcal {M}'')\) is a history in \(\mathcal {M}\) and hence belongs to \({\mathsf{hist}}(\mathcal {M}')\) because \(M''\subseteq M'\subseteq M\).
Now assume that there are \(m',m''\in M''\) s.t. \(m' \perp _m m''\) in \(\mathcal {M}\). By Definition 11 (ii), \(M_m \subseteq M''\), which implies \(M'_m \subseteq M''\) because \(M'\subseteq M\). Then \(\mathcal {M}'\) and \(\mathcal {M}''\) satisfy condition (ii) of Definition 11 as well. \(\square \)
In the remainder of this section, we show that, for any given BT structure \(\mathcal {M}\), there is a one-to-one correspondence between the set of transition sets \({\mathsf{dcts}}(\mathcal {M})\) and the set of prunings \({\mathsf{prun}}(\mathcal {M})\), as indicated in Fig. 2. The connecting link between sets of transitions and prunings is the set of histories admitted by a transition set.
Let \(\mathcal {M}\) be a BT structure. We prove that for every set of transitions \(T \in {\mathsf{dcts}}(\mathcal {M})\), the structure \(\langle \bigcup {\mathsf{H}}(T),<\rangle \) spanned by the set \({\mathsf{H}}(T)\) of histories allowed by T is a pruning of \(\mathcal {M}\) with \({\mathsf{hist}}(\langle \bigcup {\mathsf{H}}(T),<\rangle ) = {\mathsf{H}}(T)\). The correspondence between transition sets and prunings obtained along those lines is injective and reverses the inclusion relation: whenever \(T''\) is a proper extension of \(T'\), the structure \(\langle \bigcup \mathsf {H}(T''),<\rangle \) is a proper pruning of \(\langle \bigcup \mathsf {H}(T'),<\rangle \), and vice versa.
Proposition 1
Let \(\mathcal {M}=\langle M,<\rangle \) be a BT structure, and consider the function \(\chi \) with \({{{{\mathsf{Dom}}}}}(\chi ) = {{{{\mathsf{dcts}}(\mathcal {M})}}}\) defined by
The following holds:
-
(i)
for every \(T\in {{{{\mathsf{dcts}}(\mathcal {M})}}}\), \(\chi (T) \in {\mathsf{prun}}(\mathcal {M})\) and \({\mathsf{hist}}\)\((\chi (T)) = {\mathsf{H}}(T)\);
-
(ii)
\(\chi \) is injective;
-
(iii)
for all \(T',T''\in {{{{\mathsf{dcts}}(\mathcal {M})}}}\), \(T' \subsetneq T''\) iff \(\chi (T'') \subsetneq \chi (T')\).
One-to-one correspondence between transition sets and prunings. (a) \(\mathcal {M}\) with transition set T, (b) Pruning \(\mathcal {M}'\) of \(\mathcal {M}\). The BT structure \(\mathcal {M}'\) with \({\mathsf{hist}}(\mathcal {M}') = \{h_2,h_3\}\) is a pruning of \(\mathcal {M}\). It corresponds one-to-one to the transition set T in \({\mathsf{dcts}}(\mathcal {M})\) with \({\mathsf{H}}(T)= \{h_2,h_3\}\). We have \(\mathcal {M}' = \langle \bigcup {\mathsf{H}}(T),<\rangle \) and \(T = \{\langle m\!\rightarrowtail \!H\rangle \in {\mathsf{trans}\;}(\mathcal {M})\mid {\mathsf{hist}}(\mathcal {M}')\subseteq H\}.\)
Proof
(i) Take any \(T \in {\mathsf{dcts}}(\mathcal {M})\). We first show that \({\mathsf{hist}}(\chi (T)) = {\mathsf{H}}(T)\). Obviously, \({\mathsf{H}}(T)\subseteq {\mathsf{hist}}(\chi (T))\). We prove that \({\mathsf{hist}}(\chi (T))\subseteq {\mathsf{H}}(T)\) holds as well. Assume for reductio that there is some \(h\in {\mathsf{hist}}(\chi (T))\setminus {\mathsf{H}}(T)\). This implies that there is some \(\langle m\!\rightarrowtail \!H\rangle \in T\) s.t. \(h\notin H\). Hence we can consider some \(m'\in h\) s.t. \(m'\notin \bigcup H\). Since \({\mathsf{H}}(T)\subseteq H\), it follows that \(m'\notin \bigcup {\mathsf{H}}(T)\), which contradicts our assumption that \(h\in {\mathsf{hist}}(\chi (T))\).
We now show that \(\chi (T) \in {\mathsf{prun}}(\mathcal {M})\). Condition (i) of Definition 11 is trivially fulfilled because \({\mathsf{hist}}(\chi (T)) = {\mathsf{H}}(T)\ne \emptyset \). Now assume that there are <-incomparable \(m',m''\in \bigcup {\mathsf{H}}(T)\). Consider two histories \(h',h''\in {\mathsf{hist}}(\chi (T))\) s.t. \(m'\in h'\setminus h''\) and \(m''\in h''\setminus h'\), and assume \(h' \perp _m h''\) in \(\mathcal {M}\). Since \({\mathsf{hist}}(\chi (T)) = {\mathsf{H}}(T)\supseteq \{h',h''\}\), it follows that for all \(\langle m_0\!\rightarrowtail \! H_0\rangle \in T\), \(m_0 < m\). This implies that \(\mathsf {H}_m\subseteq {\mathsf{H}}(T)\). Consequently, \(M_m\subseteq \bigcup {\mathsf{H}}(T)\), which shows that condition (ii) of Definition 11 is satisfied.
Conditions (ii) and (iii) are immediate consequences of Lemma 1 given the equality \({\mathsf{hist}}(\chi (T)) = {\mathsf{H}}(T)\) established in (i). \(\square \)
We now turn to the converse correspondence: we show that every pruning \(\mathcal {M}'\) of \(\mathcal {M}\) in turn determines a transition set T in \({\mathsf{dcts}}(\mathcal {M})\) with \({\mathsf{H}}(T)= {\mathsf{hist}}(\mathcal {M}')\), viz. the set of all transitions whose outcomes include the set \({\mathsf{hist}}(\mathcal {M}')\).
Proposition 2
Let \(\mathcal {M}=\langle M,<\rangle \) be a BT structure, and consider the function \(\xi \) with \({\mathsf{Dom}}(\xi ) = {\mathsf{prun}}(\mathcal {M})\) defined by
The following holds:
-
(i)
for every \(\mathcal {M}'\in {\mathsf{prun}}(\mathcal {M})\), \(\xi (\mathcal {M}') \in {\mathsf{dcts}}(\mathcal {M})\) and \({\mathsf{H}}(\xi (\mathcal {M}')) = {\mathsf{hist}}(\mathcal {M}')\);
-
(ii)
\(\xi \) is injective;
-
(iii)
for all \(\mathcal {M}',\mathcal {M}''\in {\mathsf{prun}}(\mathcal {M})\), \(\mathcal {M}' \subsetneq \mathcal {M}''\) iff \(\xi (\mathcal {M}'') \subsetneq \xi (\mathcal {M}')\).
Proof
(i) Take any \(\mathcal {M}'\in {\mathsf{prun}}(\mathcal {M})\). It is straightforward that \(\xi (\mathcal {M}')\in {\mathsf{dcts}}(\mathcal {M})\), and obviously \({\mathsf{hist}}(\mathcal {M}')\subseteq {\mathsf{H}}(\xi (\mathcal {M}'))\). We prove that \({\mathsf{H}}(\xi (\mathcal {M}'))\subseteq {\mathsf{hist}}(\mathcal {M}')\) holds as well. Two cases can be considered. Case (i): If \(\mathcal {M}'=\mathcal {M}\), then \({\mathsf{hist}}(\mathcal {M}')= {\mathsf{hist}}(\mathcal {M})\). Consequently, \(\xi (\mathcal {M}') = \emptyset \) because there is no transition \(\langle m'\!\rightarrowtail \!H'\rangle \in {\mathsf{trans}\;}(\mathcal {M})\) s.t. \({\mathsf{hist}}(\mathcal {M})\subseteq H'\). Then, since \(\mathsf {H}(\emptyset ) = {\mathsf{hist}}(\mathcal {M})\), we have \({\mathsf{H}}(\xi (\mathcal {M}')) = {\mathsf{hist}}(\mathcal {M}')\). Case (ii): Suppose \(\mathcal {M}'\ne \mathcal {M}\), and assume for reductio that there is some \(h \in {\mathsf{H}}(\xi (\mathcal {M}'))\setminus {\mathsf{hist}}(\mathcal {M}')\). Let \(h' \in {\mathsf{hist}}(\mathcal {M}')\), and suppose \(h\perp _m h'\) in \(\mathcal {M}\). By Lemma 3 it follows that \({\mathsf{hist}}(\mathcal {M}')\subseteq [h']_m\). This implies that \(\langle m\!\rightarrowtail \! [h']_m\rangle \in \xi (\mathcal {M}')\), which contradicts the assumption that \(h\in {\mathsf{H}}(\xi (\mathcal {M}'))\).
Conditions (ii) and (iii) follow immediately from Lemma 1 on the basis of the equality \({\mathsf{H}}(\xi (\mathcal {M}')) = {\mathsf{hist}}(\mathcal {M}')\) established in (i). \(\square \)
By combining the results established in Propositions 1 and 2 above, we obtain a one-to-one correspondence between the set of transition sets \({\mathsf{dcts}}(\mathcal {M})\) and the set of prunings \({\mathsf{prun}}(\mathcal {M})\) in a given BT structure \(\mathcal {M}\).
Proposition 3
For any BT structure \(\mathcal {M}=\langle M,<\rangle \), the functions \(\chi \) and \(\xi \) are bijections and inverses of each other.
Proof
By Propositions 1 (ii) and 2 (ii) the functions \(\chi \) and \(\xi \) are injective.
Take any \(T \in {\mathsf{dcts}}(\mathcal {M})\). We show that \(\xi (\chi (T)) = T\). By Proposition 1 (i) \(\xi (\chi (T))\) equals \(\{\langle m\!\rightarrowtail \!H\rangle \in {\mathsf{trans}\;}(\mathcal {M})\mid {\mathsf{H}}(T)\subseteq H\}\). Obviously, for all \(\langle m'\!\rightarrowtail \!H'\rangle \in T\), \({\mathsf{H}}(T)\subseteq H'\), and hence \(T \subseteq \xi (\chi (T))\). We prove that \(\xi (\chi (T)) \subseteq T\) holds as well. Let \(\langle m'\!\rightarrowtail \!H'\rangle \in \xi (\chi (T))\). Then \({\mathsf{H}}(T)\subseteq H'\). Now consider some \(h\in \mathsf {H}_{m'}\setminus H'\). It follows that \(h\notin {\mathsf{H}}(T)\). Let \(h'\in {\mathsf{H}}(T)\subseteq H' \subsetneq \mathsf {H}_{m'}\). Then \(h \perp _{m'} h'\). Accordingly, there must be some \(\langle m''\!\rightarrowtail \!H''\rangle \in T\) s.t. \(h \not \in H''\) and \(h'\in H''\). Then \(\langle m'\!\rightarrowtail \!H'\rangle \preceq \langle m''\!\rightarrowtail \!H''\rangle \). Since T is \(\prec \)-downward closed, this implies that \(\langle m'\!\rightarrowtail \!H'\rangle \in T\).
We now verify that for all \(\mathcal {M}'\in {\mathsf{prun}}(\mathcal {M})\), \(\chi (\xi (\mathcal {M}')) = \mathcal {M}'\). Note that by Proposition 2 (i), for all \(\mathcal {M}'\in {\mathsf{prun}}(\mathcal {M})\), \(\chi (\xi (\mathcal {M}'))=\langle \bigcup {\mathsf{hist}}(\mathcal {M}'),<\rangle \), and so the claim is trivially fulfilled. \(\square \)
4 Index Structures
Drawing on the correspondence between transition sets and prunings established in Sect. 3, we now put forth the definition of an index structure. Unlike transition structures, index structures are genuine Kripke structures: in an index structure, sentences of the transition language \(\mathcal {L}_\mathsf{t}\) are evaluated at the points of the structure, and quantification over transition sets dissolves into restricted first-order quantification over that set.
An index structure is a Kripke structure \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) consisting of a non-empty set W and three primitive relations: \(\lhd \), \(\sim \) and \(\sqsubseteq \). A fourth relation \(\approx \) on W can be defined along the following lines: for all \(w,w'\in W\),
For any \(w\in W\), we denote the set \(\{w'\in W\mid w \approx w'\}\) by \([w]_\approx \). The notation suggests that \(\approx \) is an equivalence relation, and we will see below that this in fact the case [cf. (4.2)]. We state the definition of an index structure outright and then discuss its implications.
An index structure. Endowed with the order relation \(\lhd \subseteq \ \approx \), each equivalence class in \({W/\!\!\approx }\) forms a BT structure, and the internal relation \(\sqsubseteq \ \subseteq \ \sim \) on the equivalence classes in \({W/\!\!\sim }\) defines a tree-like ordering beween those BT structures.
Definition 12
(Index structure) An index structure is a quadruple \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) s.t.
-
(i)
\(W \ne \emptyset \);
-
(ii)
the relation \(\lhd \) is a left-linear and serial strict partial order on W;
-
(iii)
the relation \(\sim \) is an equivalence relation on W, and we denote the \(\sim \)-equivalence class of an element \(w\in W\) by \([w]_\sim \);
-
(iv)
the relation \(\sqsubseteq \) is a left-linear partial order on W;
-
(v)
\(\sqsubseteq \ \subseteq \ \sim \);
-
(vi)
for all \(w,w' \in W\), there is some \(x \in [w]_\approx \) and there is some \(x' \in [w']_\approx \) s.t. (i) \(x \unlhd w\) and \(x' \unlhd w'\), (ii) \(x \sim x'\) and (iii) for all \(y,y' \in W\) s.t. \(y \unlhd w\), \(y' \unlhd w'\) and \(y \sim y'\), we have \(y \unlhd x\) and \(y' \unlhd x'\);
-
(vii)
for all \(w,w' \in W\), the intersection \(\sim \cap \ ([w]_\approx \times [w']_\approx )\) is a (non-empty) \(\lhd \)-isomorphism \(f_{w,w'}\) s.t.
-
(a)
if \(\sqsupset \cap \ ([w]_\approx \times [w']_\approx ) \not = \emptyset \), then (i) \(f_{w,w'} = \ \sqsupset \cap \ ([w]_\approx \times [w']_\approx )\), (ii) \({\mathsf{Dom}}(f_{w,w'}) = [w]_\approx \) and (iii) \(\langle \mathsf {Im}(f_{w,w'}), \lhd \rangle \) is a proper pruning of \(\langle [w']_\approx , \lhd \rangle \);
-
(b)
if \(\sqsupset \cap \ ([w]_\approx \times [w']_\approx ) = \emptyset \), \(\sqsupset \cap \ ([w']_\approx \times [w]_\approx ) = \emptyset \) and \([w]_\approx \ne [w']_\approx \), then (i) \({\mathsf{Dom}}(f_{w,w'})\ne [w]_\approx \) and \(\mathsf {Im}(f_{w,w'})\ne [w']_\approx \), (ii) \({\mathsf{Dom}}(f_{w,w'})\) [\(\mathsf {Im}(f_{w,w'})\)] is a \(\lhd \)-downward closed subset of \(\mathsf {Trunk}(\langle [w]_\approx , \lhd \rangle )\) [\(\mathsf {Trunk}(\langle [w']_\approx , \lhd \rangle )\)] and (iii) for all \(x,x',x''\in [w]_\approx \), \(x'\perp _x x''\) implies \(x\not \in {\mathsf{Dom}}(f_{w,w'})\), and for all \(y,y',y''\in [w']_\approx \), \(y'\perp _y y''\) implies \(y\notin \mathsf {Im}(f_{w,w'})\).
-
(a)
In an abstract sense, an index structure is but a tree of trees: it is a tree-like arrangement of disjoint BT structures, as shown in Fig. 3. It is readily verified that
By (4.1), the relation \(\approx \) is obviously reflexive and symmetric. The transitivity of \(\approx \) is a straightforward consequence of the left-linearity of \(\lhd \). On the whole, we are then provided with two equivalence relations, \(\approx \) and \(\sim \), and two order relations, \(\lhd \subseteq \ \approx \) and \(\sqsubseteq \ \subseteq \ \sim \), which bestow an internal structure on the respective equivalence classes. As we shall see, for every equivalence class \([w]_\approx \in {W/\!\!\approx }\), the structure \(\langle [w]_\approx ,\lhd \rangle \) is a BT structure (cf. Lemma 6), and the relation \(\sqsubseteq \) on the \(\sim \)-equivalence classes induces a left-linear partial order among those BT structures, which corresponds—up to isomorphism—to the converse of the pruning relation.
The interaction of \(\lhd , \sim , \sqsubseteq \) and \(\approx \). (a) \(\sqsubset \)-comparable structures. For \(w_1 \sqsupset w_2\), the relation \(\sim \) induces an \(\lhd \)-isomorphism \(\sqsupset \cap \ ([w_1]_\approx \times [w_2]_\approx )\) from \(\langle [w_1]_\approx ,\lhd \rangle \) onto a pruning of \(\langle [w_2]_\approx ,\lhd \rangle \). (b) \(\sqsubset \)-incomparable structures. For \(w_2 \not \sqsupset w_5\) and \(w_5 \not \sqsupset w_2\), the relation \(\sim \) induces an \(\lhd \)-isomorphism between initial segments of the trunks of \(\langle [w_2]_\approx ,\lhd \rangle \) and \(\langle [w_5]_\approx ,\lhd \rangle \).
But let us have a more detailed look at conditions (vi) and (vii) of Definition 12, which capture the interaction of the different relations imposed on W. Condition (vi), first of all, guarantees that, for any two distinct BT structures \(\langle [w]_\approx ,\lhd \rangle \) and \(\langle [w']_\approx ,\lhd \rangle \), the intersection \(\sim \cap \ ([w]_\approx \times [w']_\approx )\) is non-empty. On the basis of condition (v), we can then distinguish two cases, which correspond to the two conditions provided in clause (vii). The two cases are illustrated in Fig. 4. (a) If the intersection \(\sqsupset \cap \ ([w]_\approx \times [w']_\approx )\) is non-empty as well, the relation \(\sqsupset \) induces an order isomorphism between \(\langle [w]_\approx ,\lhd \rangle \) and a proper pruning of \(\langle [w']_\approx ,\lhd \rangle \). (b) If both the intersections \(\sqsupset \cap \ ([w]_\approx \times [w']_\approx )\) and \(\sqsupset \cap \ ([w']_\approx \times [w]_\approx )\) are empty, the relation \(\sim \) defines an order isomorphism between initial segments of the trunks of \(\langle [w]_\approx ,\lhd \rangle \) and \(\langle [w']_\approx ,\lhd \rangle \) such that neither of the two BT structures is embeddable into the other.Footnote 7 One qualification is in order here: the trunks of \(\langle [w]_\approx ,\lhd \rangle \) and \(\langle [w']_\approx ,\lhd \rangle \) may contain branching points as maxima and, against the background of Lemma 3, those need to be excluded from the domain and image of the function \(\sim \cap \ ([w]_\approx \times [w']_\approx )\).Footnote 8 Note that in the context of condition (vii.b), clause (vi) forces the trunks of \(\langle [w]_\approx ,\lhd \rangle \) and \(\langle [w']_\approx ,\lhd \rangle \) to be non-empty and implies, moreover, that the intersection \(\sim \cap \ ([w]_\approx \times [w']_\approx )\) on those trunks contains a \(\lhd \)-maximal pair.
In the following lemmas, we state some results about index structures that will become important in the remainder of the paper.
Lemma 5
For \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) an index structure and \(w,w'\in W\), we have either \([w]_\sim \cap [w']_\approx =\emptyset \) or \([w]_\sim \cap [w']_\approx = \{v\}\) for some \(v\in W\).
Proof
Assume \([w]_\sim \cap [w']_\approx \ne \emptyset \). Then \(w\in {\mathsf{Dom}}(f_{w,w'})\). Assume for reductio that \([w]_\sim \cap [w']_\approx \supseteq \{v,u\}\). This implies that \(f_{w,w'}(w) = u\) and \(f_{w,w'}(w) = v\), which contradicts the fact that \(f_{w,w'}\) is a function. \(\square \)
Lemma 6
Let \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) be an index structure. For every \(w\in W\), the structure \(\langle [w]_\approx ,\lhd \rangle \) is a BT structure.
Proof
By Definition 12 (ii), the relation \(\lhd \) is a left-linear and serial strict partial order. The jointedness of \(\lhd \) follows from Definition 12 (vi) on the basis of Lemma 5. \(\square \)
Lemma 7
For \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) an index structure and \(w,w'\in W\), the following holds:
-
(i)
if \(w' \lhd w\), then for all \(x \in [w]_\sim \), there is some \(x' \in [w']_\sim \) s.t. \(x' \lhd x\);
-
(ii)
if \(w' \sqsubseteq w\), then for all \(x\in [w]_\approx \), there is some \(x'\in [w']_\approx \) s.t. \(x' \sqsubseteq x\).
Proof
(i) Assume \(w' \lhd w\), and let \(x\in [w]_\sim \). Then \(w\in {\mathsf{Dom}}(f_{w,x})\) and \(f_{w,x}(w) = x\). By Definition 12 (vii), the function \(f_{w,x}\) is an \(\lhd \)-isomorphism whose domain is downward closed. Consequently, \(w'\in {\mathsf{Dom}}(f_{w,x})\) and \(f_{w,x}(w') \lhd x\). Let \(x'\) be \(f_{w,x}(w')\).
(ii) The case \(w'=w\) is trivial: let \(x'\) be x. Now assume \(w' \sqsubset w\), and let \(x\in [w]_\approx \). Then, by Definition 12 (vii.a), \(f_{w,w'} = \ \sqsupset \cap \ ([w]_\approx \times [w']_\approx )\) is an \(\lhd \)-isomorphism with \({\mathsf{Dom}}(f_{w,w'}) = [w]_\approx \). Let \(x'\) be \(f_{w,w'}(x)\). \(\square \)
In an index structure \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \), sentences of the transition language \(\mathcal {L}_\mathsf{t}\) are evaluated at the elements of W. The temporal operators \(\mathsf {P}\), \(\mathsf {f}\) and \({\mathsf{F}}\) shift the index of evaluation along the relation \(\lhd \), the inevitability operator \(\Box \) shifts the index of evaluation along the relation \(\sim \) and the stability operator \(\mathsf {S}\) along the relation \(\sqsubseteq \). While the operators \(\mathsf {P}\), \(\mathsf {f}\), \(\Box \) and \(\mathsf {S}\) are genuine Kripke-style operators, the strong future operator \({\mathsf{F}}\) is not: its index semantics is a Peircean-like semantics that involves second-order quantification over histories. This is to say, the semantics of the strong future operator \({\mathsf{F}}\) does not reduce to the relations \(\lhd \), \(\sim \) and \(\sqsubseteq \) on W. We will deal with that complication in Sect. 7 below.Footnote 9
Definition 13
(Index model) An index model is a quintuple \(\mathfrak {W} =\)\(\langle W,\lhd ,\sim ,\sqsubseteq ,v_{{\mathsf{i}}}\rangle \) where \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) is an index structure and \(v_{{\mathsf{i}}}: \mathsf {At}\times W \rightarrow \{0,1\}\) a valuation function.
The following semantic clauses extend the valuation \(v_{{\mathsf{i}}}\) on the propositional variables \(p\in \mathsf {At}\) in an index model \(\mathfrak {W}\) to any arbitrary sentence \(\phi \in \mathcal {L}_\mathsf{t}\):
- (\(\mathsf {At}\)):
-
\(\mathfrak {W},w \vDash _{{\mathsf{i}}}p\) iff \(v_{{\mathsf{i}}}(p,w) = 1\);
- (\(\lnot \)):
-
\(\mathfrak {W},w \vDash _{{\mathsf{i}}}\lnot \phi \) iff \(\mathfrak {W},w \not \vDash _{{\mathsf{i}}}\phi \);
- (\(\wedge \)):
-
\(\mathfrak {W},w \vDash _{{\mathsf{i}}}\phi \wedge \psi \) iff \(\mathfrak {W},w \vDash _{{\mathsf{i}}}\phi \) and \(\mathfrak {W},w \vDash _{{\mathsf{i}}}\psi \);
- (\(\mathsf {P}\)):
-
\(\mathfrak {W},w \vDash _{{\mathsf{i}}}\mathsf {P}\phi \) iff there is some \(w'\in W\) s.t. \(w'\lhd w\) and \(\mathfrak {W},w' \vDash _{{\mathsf{i}}}\phi \);
- (\(\mathsf {f}\)):
-
\(\mathfrak {W},w \vDash _{{\mathsf{i}}}\mathsf {f}\phi \) iff there is some \(w'\in W\) s.t. \(w'\rhd w\) and \(\mathfrak {W},w' \vDash _{{\mathsf{i}}}\phi \);
- (\({\mathsf{F}}\)):
-
\(\mathfrak {W},w \vDash _{{\mathsf{i}}}{\mathsf{F}}\phi \) iff for all \(h\in {\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle )\) s.t. \(w\in h\), there is some \(w'\in h\) s.t. \(w'\rhd w\) and \(\mathfrak {W},w' \vDash _{{\mathsf{i}}}\phi \);
- (\(\Box \)):
-
\(\mathfrak {W},w \vDash _{{\mathsf{i}}}\Box \phi \) iff for all \(w' \sim w\), \(\mathfrak {W},w' \vDash _{{\mathsf{i}}}\phi \);
- (\(\mathsf {S}\)):
-
\(\mathfrak {W},w \vDash _{{\mathsf{i}}}\mathsf {S}\phi \) iff for all \(w' \sqsupseteq w\), \(\mathfrak {W},w' \vDash _{{\mathsf{i}}}\phi \).
5 Transition Structures and Index Structures
In this section, we show that there is a one-to-one correspondence up to isomorphism between transition structures and index structures that preserves \(\mathcal {L}_\mathsf{t}\)-validity.Footnote 10 The proof proceeds in several steps: we first show that to every transition structure, there naturally corresponds an index structure (cf. Definition 14 and Theorem 1). We then establish the converse correspondence (cf. Definition 15 and Theorem 2). Finally, we show that the two correspondences are inverses of each other up to isomorphism (cf. Theorem 3) and that \(\mathcal {L}_\mathsf{t}\)-validity is preserved (Proposition 4 and Theorem 4).
Let \(\mathcal {M}^{\textit{ts}}= \langle M,<,{\textit{ts}}\rangle \) be a transition structure. We show that \(\mathcal {M}^{\textit{ts}}\) determines an index structure \(\langle {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}}),\lhd ,\sim ,\sqsubseteq \rangle \) on the set \({\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\) of indices of evaluation in \(\mathcal {M}^{\textit{ts}}\), where the relations \(\lhd , \sim \) and \(\sqsubseteq \) are defined in terms of the relations < on M and \(\subseteq \) on \({\textit{ts}}\) between moments and transition sets, respectively.
Definition 14
For any transition structure \(\mathcal {M}^{\textit{ts}}= \langle M,<,{\textit{ts}}\rangle \), let \(\lambda (\mathcal {M}^{\textit{ts}})\) be the structure \(\langle {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}}),\lhd ,\sim ,\sqsubseteq \rangle \) with
- (\(\lhd \)):
-
\(m/T \lhd m'/T'\) iff \(T=T'\) and \(m<m'\);
- (\(\sim \)):
-
\(m/T \sim m'/T'\) iff \(m=m'\);
- (\(\sqsubseteq \)):
-
\(m/T \sqsubset m'/T'\) [\(m/T = m'/T'\)] iff \(m=m'\) and \(T\subset T'\) [\(T = T'\)].
In the context of Definition 14, the relation \(\approx \) defined in (4.1) captures sameness of transition set, i.e. for all \(m/T,m'/T'\in {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\),
A verification of that claim will be provided within the proof of following theorem.
Theorem 1
For every transition structure \(\mathcal {M}^{\textit{ts}}= \langle M,<,{\textit{ts}}\rangle \), the structure \(\lambda (\mathcal {M}^{\textit{ts}})\) is an index structure.
Proof
It is readily verified that the structure \(\lambda (\mathcal {M}^{\textit{ts}}) = \langle {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}}),\lhd ,\sim ,\sqsubseteq \rangle \) fulfills conditions (i)–(vi) of Definition 12. Condition (i) is guaranteed by the definition of a transition structure (Definition 9). Condition (ii) follows immediately from the corresponding properties of the relation < on M (Definition 1), while condition (iv) is a consequence of the properties of the inclusion relation \(\subseteq \) on \({\textit{ts}}\). Conditions (iii) and (v) are straightforward by definition. Condition (vi) follows from the jointedness of the relation < on M (Definition 1), taking into account that for all \(T\in {\textit{ts}}\), if \(m'<m\) and \(m/T \in {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\), then \(m'/T \in {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\). It remains to be shown that \(\lambda (\mathcal {M}^{\textit{ts}})\) satisfies condition (vii) of Definition 12.
As an intermediate step, we establish some results about the defined relation \(\approx \) on \({\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\). In the present context, (4.1) reads: \(m/T \approx m'/T'\) iff there is some \(m''/T''\in {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\) s.t. \(m/T \,\unrhd \, m''/T'' \,\unlhd \, m'/T'\). We first verify that the relation \(\approx \) captures samesness of transition set, as stated in (5.1) above. By the definition of \(\lhd \) on \({\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\) (Definition 14) it is straightforward that \(m/T \approx m'/T'\) implies \(T = T'\). The converse implication is an immediate consequence of condition (vi) of Definition 12. The defined relation \(\approx \) on \({\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\) thus qualifies as an equivalence relation. We show that for every equivalence class \([m/T]_\approx \in {{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\approx }\), the structure \(\langle [m/T]_\approx ,\lhd \rangle \) is order isomorphic to a pruning of \(\mathcal {M}\). Let \(\theta : {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\rightarrow M\) be the function defined by
Obviously, \(\theta \vert _{[m/T]_\approx }\) is injective and order-preserving: for all \(m'/T,m''/T\in [m/T]_\approx \), \(m'/T \lhd m''/T\) implies \(\theta (m'/T) < \theta (m''/T)\). We show that
From (5.1) it follows that \(\theta ([m/T]_\approx ) = \bigcup {\mathsf{H}}(T)\), and, by Proposition 1 (i), the structure \(\langle \bigcup {\mathsf{H}}(T),<\rangle \) is a pruning of \(\mathcal {M}\).
With those preliminaries in place, we now prove that \(\lambda (\mathcal {M}^{\textit{ts}})\) satisfies condition (vii) of Definition 12. Take any \(m/T, m'/T' \in {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\), and consider the intersection \(\sim \cap \ ([m/T]_\approx \times [m'/T']_\approx )\), which figures in condition (vii) of Definition 12. By condition (vi) of that definition it is guaranteed that the intersection is non-empty. Moreover, by (5.1) and the definition of \(\sim \) on \({\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\) (Definition 14), for all \(m_0/T_0, m_1/T_1\in {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\), \(\langle m_0/T_0,m_1/T_1\rangle \in \ \sim \cap \ ([m/T]_\approx \times [m'/T']_\approx )\) implies \(T_0 = T\), \(T_1=T'\) and \(m_0=m_1\). Then \(\sim \cap \ ([m/T]_\approx \times [m'/T']_\approx )\) is an injective and \(\lhd \)-preserving function, and we denote it by \(f_{m/T,\, m'/T'}\). The first part of condition (vii) thus holds for \(\lambda (\mathcal {M}^{\textit{ts}})\).
We now turn to condition (vii.a). Assume \(\sqsupset \cap \ ([m/T]_\approx \times [m'/T']_\approx ) \ne \emptyset \). Then \(T\supsetneq T'\). Consequently, by Lemma 1, \({\mathsf{H}}(T)\subsetneq \mathsf {H}(T')\), and hence \(\bigcup {\mathsf{H}}(T)\subsetneq \bigcup \mathsf {H}(T')\). From this it follows that \(f_{m/T,\, m'/T'} = \ \sqsupset \cap \ ([m/T]_\approx \times [m'/T']_\approx )\) with \({\mathsf{Dom}}(f_{m/T,\, m'/T'}) = [m/T]_\approx \). We prove that \(\langle \mathsf {Im}(f_{m/T,\, m'/T'}),\lhd \rangle \) is a proper pruning of \(\langle [m'/T']_\approx ,\lhd \rangle \). By (5.3) both \(\langle \theta ([m/T]_\approx ),<\rangle \) and \(\langle \theta ([m'/T']_\approx ),<\rangle \) are prunings of \(\mathcal {M}\), and since \(\bigcup {\mathsf{H}}(T)\subsetneq \bigcup \mathsf {H}(T')\), we have \(\langle \theta ([m/T]_\approx ),<\rangle \subsetneq \langle \theta ([m'/T']_\approx ),<\rangle \). This implies by Lemma 4 that the structure \(\langle \theta ([m/T]_\approx ),<\rangle \) is a proper pruning of \(\langle \theta ([m'/T']_\approx ),<\rangle \). The claim then follows immediately because \(f_{m/T,\, m'/T'} = \theta ^{-1}\vert _{[m'/T']_\approx } \circ \theta \vert _{[m/T]_\approx }\).
Let us finally consider condition (vii.b). Assume \(\sqsupset \cap \ ([m/T]_\approx \times [m'/T']_\approx ) = \emptyset \) and \(\sqsupset \cap \ ([m'/T']_\approx \times [m/T]_\approx ) = \emptyset \) with \([m/T]_\approx \ne [m'/T']_\approx \). Then \(T \not \subseteq T'\) and \(T' \not \subseteq T\), and hence, by Lemma 1, \({\mathsf{H}}(T)\not \subseteq \mathsf {H}(T')\) and \(\mathsf {H}(T')\not \subseteq {\mathsf{H}}(T)\). Let \(h\in {\mathsf{H}}(T)\setminus \mathsf {H}(T')\), \(h'\in \mathsf {H}(T')\setminus {\mathsf{H}}(T)\), and suppose \(h\perp _{m_0} h'\). Since, by Proposition 1 (i), both \(\langle \bigcup {\mathsf{H}}(T),<\rangle \) and \(\langle \bigcup \mathsf {H}(T'),<\rangle \) are proper prunings of \(\mathcal {M}\) with \({\mathsf{hist}}(\langle \bigcup {\mathsf{H}}(T),<\rangle ) = {\mathsf{H}}(T)\) and \({\mathsf{hist}}(\langle \bigcup \mathsf {H}(T'),<\rangle ) = \mathsf {H}(T')\), by Lemma 3 it follows that \({\mathsf{H}}(T)\subseteq [h]_{m_0}\) and \(\mathsf {H}(T')\subseteq [h']_{m_0}\). That is, for all \(h_1\in {\mathsf{H}}(T)\) and \(h_1'\in \mathsf {H}(T')\), \(h_1\perp _{m_0} h_1'\), and for all \(h_2,h_3\in {\mathsf{H}}(T)\), if \(h_2 \perp _{m_1} h_3\), then \(m_0 < m_1\); and similarly for \(\mathsf {H}(T')\). Because, by (5.3), \(\theta \vert _{[m/T]_\approx }\) and \(\theta \vert _{[m'/T']_\approx }\) are order isomorphisms onto \(\bigcup {\mathsf{H}}(T)\) resp. \(\bigcup \mathsf {H}(T')\), this implies that \(\sim \cap \ ([m/T]_\approx \times [m'/T']_\approx )\) is identical to \(\{\langle m''/T, m''/T' \rangle \mid m'' \le m_0\}\). We have \(m_0/T \in \mathsf {Trunk}(\langle [m/T]_\approx ,\lhd \rangle )\), and so \({\mathsf{Dom}}(f_{m/T,\, m'/T'}) = \{m''/T\mid m''\le m_0\}\) is a \(\lhd \)-downward closed subset of \(\mathsf {Trunk}(\langle [m/T]_\approx ,\lhd \rangle )\). Moreover, for all \(m_1/T, m_2/T,m_3/T \in [m/T]_\approx \) s.t. \(m_2/T \perp _{m_1/T} m_3/T\), it holds that \(m_1/T \notin {\mathsf{Dom}}(f_{m/T,\, m'/T'})\). The proof for \(\mathsf {Im}(f_{m/T,\, m'/T'})\) is analogous. \(\square \)
Concerning the converse correspondence, we show that, given an index structure \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \), we can lift a BT structure \(\langle {W/\!\!\sim },\ll \rangle \) from the \(\sim \)-equivalence classes in W and extract a set of transition sets \(\mathsf {ts}({W/\!\!\approx })\) in that BT structure from the \(\approx \)-equivalence classes in W.
Definition 15
For any index structure \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \), let \(\zeta (\mathcal {W})\) be the structure \(\langle {W/\!\!\sim },\ll ,\mathsf {ts}({W/\!\!\approx })\rangle \) with
- (\(\ll \)):
-
\([w]_\sim \ll [w']_\sim \) iff there is some \(x \in [w]_\sim \) and some \(x' \in [w']_\sim \) s.t. \(x \lhd x'\);
and
where \(\xi \) is the function defined in (3.2) and \(\sigma : W \rightarrow {W/\!\!\sim }\) is defined by
For every \([w]_\approx \in {W/\!\!\approx }\), the structure \(\langle \sigma ([w]_\approx ), \ll \rangle \) will be denoted by \(\mathcal {T} _{[w]_\approx }\) and the corresponding element \(\xi (\langle \sigma ([w]_\approx ), \ll \rangle ) \in \mathsf {ts}({W/\!\!\approx })\) by \(T_{[w]_\approx }\).Footnote 11
Being defined in terms of quantification over the elements of \(\sim \)-equivalence classes, the relation \(\ll \) is clearly well-defined. It will be shown below that the structure \(\langle {W/\!\!\sim },\ll \rangle \) is in fact a BT structure [cf. (5.6)] and that for every \([w]_\approx \in {W/\!\!\approx }\), \(\mathcal {T} _{[w]_\approx } \in {\mathsf{prun}}(\langle {W/\!\!\sim },\ll \rangle )\) [cf. (5.7)]. This warrants the application of the function \(\xi \), which then for every \([w]_\approx \in {W/\!\!\approx }\), yields a transition set \(T_{[w]_\approx } \in \mathsf {dcts}(\langle {W/\!\!\sim },\ll \rangle )\) with \({\mathsf{H}}(T_{[w]_\approx }) = {\mathsf{hist}}(\mathcal {T} _{[w]_\approx })\) [cf. (5.11)].
An auxiliary relation  on \({W/\!\!\approx }\) can be defined along the following lines:
on \({W/\!\!\approx }\) can be defined along the following lines:

Note that by Definition 12, we have \([w]_\approx \Subset [w']_\approx \) iff there is some \(x \in [w]_\approx \) and some \(x' \in [w']_\approx \) s.t. \(x \sqsubset x'\). Just as the relation \(\ll \) on \({W/\!\!\sim }\), the relation  on \({W/\!\!\approx }\) is obviously well-defined. Whereas the relation \(\ll \) on \({W/\!\!\sim }\) represents the temporal ordering on the set of moments \({W/\!\!\sim }\), the relation
on \({W/\!\!\approx }\) is obviously well-defined. Whereas the relation \(\ll \) on \({W/\!\!\sim }\) represents the temporal ordering on the set of moments \({W/\!\!\sim }\), the relation  on \({W/\!\!\approx }\) induces an ordering among the various transition sets in \(\mathsf {ts}({W/\!\!\approx })\), as we shall see. Recall that by Lemma 7, the following holds:
on \({W/\!\!\approx }\) induces an ordering among the various transition sets in \(\mathsf {ts}({W/\!\!\approx })\), as we shall see. Recall that by Lemma 7, the following holds:
-
(i)
\([w]_\sim \ll [w']_\sim \) iff for all \(x' \in [w']_\sim \), there is some \(x\in [w]_\sim \) s.t. \(x \lhd x'\);
-
(ii)
 iff for all \(x'\in [w']_\approx \), there is some \(x \in [w]_\approx \) s.t. \(x \sqsubseteq x'\).
iff for all \(x'\in [w']_\approx \), there is some \(x \in [w]_\approx \) s.t. \(x \sqsubseteq x'\).
Theorem 2
For every index structure \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \), the structure \(\zeta (\mathcal {W})\) is a transition structure.
Proof
We first show that
Obviously, \({W/\!\!\sim }\ne \emptyset \). That the relation \(\ll \) is a left-linear and serial strict partial order on \({W/\!\!\sim }\) follows from the corresponding properties of the relation \(\lhd \) on W [Definition 12 (ii)] on the basis of Lemmas 5 and 7 (i). The jointedness of the relation \(\ll \) is a straightforward consequence of Definition 12 (vi) and Lemma 7 (i).
We now prove that \(\mathsf {ts}({W/\!\!\approx })\) yields a set of transition sets in the BT structure \(\langle {W/\!\!\sim },\ll \rangle \), i.e. \(\mathsf {ts}({W/\!\!\approx }) \subseteq \mathsf {dcts}(\langle {W/\!\!\sim },\ll \rangle )\). To this end, we show that for every \([w]_\approx \in {W/\!\!\approx }\),
By Lemma 5, it is straightforward that \(\sigma \vert _{[w]_\approx }\) is injective and order-preserving: for all \(x,x'\in [w]_\approx \), \(x \lhd x'\) implies \(\sigma (x) \ll \sigma (x')\). Then, by Lemma 6, \(\mathcal {T} _{[w]_\approx } \subseteq \langle {W/\!\!\sim },\ll \rangle \) is a BT structure. Moreover, on the basis of Lemmas 5 and 7 (ii), from Definition 12 (iv) it follows that the relation  on \({W/\!\!\approx }\) is a left-linear partial order, and, by Definition 12 (vii),
on \({W/\!\!\approx }\) is a left-linear partial order, and, by Definition 12 (vii),
In order to prove (5.7), we establish the following two claims. For every maximal  -chain C in \({W/\!\!\approx }\),
-chain C in \({W/\!\!\approx }\),
Proof of (5.9). Consider any history h in \(\mathcal {T} _{[w]_\approx }\), and let \(h'\) be any history in \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\) s.t. \(h \subseteq h'\). Assume for reductio that there is some \([v]_\sim \in h'\setminus h\). Then there must be some \([w']_\approx \in C\) s.t. \(\mathcal {T} _{[w']_\approx }\) contains \([v]_\sim \). It follows that \(\mathcal {T} _{[w]_\approx }\) is a proper pruning of \(\mathcal {T} _{[w']_\approx }\). By Lemma 2 this implies that \(h\in {\mathsf{hist}}(\mathcal {T} _{[w']_\approx })\), which contradicts the assumption that \([v]_\sim \notin h\) because \(h \cup \{[v]_\sim \}\) is \(\ll \)-linearly ordered. Consequently, \(h=h'\), and hence condition (i) of Definition 11 is satisfied by \(\mathcal {T} _{[w]_\approx }\) and \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\).
Now assume that there are \(\ll \)-incomparable \([v']_\sim ,[v'']_\sim \) in \(\mathcal {T} _{[w]_\approx }\), and suppose \([v']_\sim \perp _{[v]_\sim }[v'']_\sim \) in \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\). Take any \([z]_\sim \) in \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\) that is \(\ll \)-comparable with \([v]_\sim \), and consider some \([w']_\approx \in C\) s.t. \([v]_\sim \), \([v']_\sim \), \([v'']_\sim \), \([z]_\sim \) in \(\mathcal {T} _{[w']_\approx }\). Then \(\mathcal {T} _{[w]_\approx }\) is a pruning of \(\mathcal {T} _{[w']_\approx }\) and \([v']_\sim \perp _{[v]_\sim }[v'']_\sim \) in \(\mathcal {T} _{[w']_\approx }\). Hence, by Definition 11 (ii), \([z]_\sim \) in \(\mathcal {T} _{[w]_\approx }\). This shows that \(\mathcal {T} _{[w]_\approx }\) and \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\) fulfill condition (ii) of Definition 11 as well.
Proof of (5.10). Let \([w]_\approx \in C\) and \(h\in {\mathsf{hist}}(\mathcal {T} _{[w]_\approx })\). Then, by (5.9) and Lemma 2, h is a history in \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\). Consider any history \(h'\) in \(\langle {W/\!\!\sim },\ll \rangle \) s.t. \(h \subseteq h'\). Assume for reductio that there is some \([v]_\sim \in h'\setminus h\). Then there must be some \([w']_\approx \in {W/\!\!\approx }\) s.t. \([w]_\approx \) and \([w']_\approx \) are  -incomparable and \([v]_\sim \) is contained in \(\mathcal {T} _{[w']_\approx }\). No matter whether \({\mathsf{hist}}(\mathcal {T} _{[w]_\approx }) = \{h\}\) or whether \(\mathcal {T} _{[w]_\approx }\) contains another history, by Definition 12 (vii.b), there is some \(z \in [w]_\approx \) s.t. \(z \notin {\mathsf{Dom}}(f_{w,w'})\) and \([z]_\sim \in h\). Since \([v]_\sim \notin h\) and histories are downward closed, \([z]_\sim \ll [v]_\sim \), which, by Lemma 7 (i), contradicts \(z \notin {\mathsf{Dom}}(f_{w,w'})\). Then \(h=h'\), and hence \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\) and \(\langle {W/\!\!\sim },\ll \rangle \) satisfy Definition 11 (i).
-incomparable and \([v]_\sim \) is contained in \(\mathcal {T} _{[w']_\approx }\). No matter whether \({\mathsf{hist}}(\mathcal {T} _{[w]_\approx }) = \{h\}\) or whether \(\mathcal {T} _{[w]_\approx }\) contains another history, by Definition 12 (vii.b), there is some \(z \in [w]_\approx \) s.t. \(z \notin {\mathsf{Dom}}(f_{w,w'})\) and \([z]_\sim \in h\). Since \([v]_\sim \notin h\) and histories are downward closed, \([z]_\sim \ll [v]_\sim \), which, by Lemma 7 (i), contradicts \(z \notin {\mathsf{Dom}}(f_{w,w'})\). Then \(h=h'\), and hence \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\) and \(\langle {W/\!\!\sim },\ll \rangle \) satisfy Definition 11 (i).
Now assume that there are \(\ll \)-incomparable \([v']_\sim \), \([v'']_\sim \) in \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\). Then there is some \([w]_\approx \in C\) s.t. \([v']_\sim , [v'']_\sim \) in \(\mathcal {T} _{[w]_\approx }\). Suppose \([v']_\sim \perp _{[v]_\sim }[v'']_\sim \) in \(\langle {W/\!\!\sim },\ll \rangle \), and let y be the unique element in \([v]_\sim \cap [w]_\approx \), which exists by Lemma 5. Note that, by Lemma 7 (i), for all \([u]_\sim \) in \(\langle {W/\!\!\sim },\ll \rangle \) s.t. \([u]_\sim \ll [v]_\sim \), \([u]_\sim \) in \(\mathcal {T} _{[w]_\approx }\). Now assume for reductio that there is some \([z]_\sim \) in \(\langle {W/\!\!\sim },\ll \rangle \) s.t. \([v]_\sim \ll [z]_\sim \) and that \([z]_\sim \) is not contained in \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\). Then there must be some \([w']_\approx \in {W/\!\!\approx }\) s.t. \([w]_\approx \) and \([w']_\approx \) are  -incomparable and \([z]_\sim \) is contained in \(\mathcal {T} _{[w']_\approx }\). By Definition 12 (vii.b), \(y\notin {\mathsf{Dom}}(f_{w,w'})\), which, by Lemma 7 (i), contradicts the assumption \([v]_\sim \ll [z]_\sim \). This shows that \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\) and \(\langle {W/\!\!\sim },\ll \rangle \) also fulfill condition (ii) of Definition 11.
-incomparable and \([z]_\sim \) is contained in \(\mathcal {T} _{[w']_\approx }\). By Definition 12 (vii.b), \(y\notin {\mathsf{Dom}}(f_{w,w'})\), which, by Lemma 7 (i), contradicts the assumption \([v]_\sim \ll [z]_\sim \). This shows that \(\bigcup _{[x]_\approx \in C} \mathcal {T} _{[x]_\approx }\) and \(\langle {W/\!\!\sim },\ll \rangle \) also fulfill condition (ii) of Definition 11.
From (5.9) and (5.10), the claim in (5.7) follows immediately by the transitivity of the pruning relation. On the basis of Proposition 2 (i), (5.7) implies that for all \([w]_\approx \in {W/\!\!\approx }\),
The proof can now be concluded by observing that for every \([w]_\sim \in {W/\!\!\sim }\), \({\mathsf{H}}(T_{[w]_\approx }) \cap \mathsf {H}_{[w]_\sim } \ne \emptyset \), which is a consequence of (5.11). \(\square \)
The correspondences \(\lambda \) and \(\zeta \) established in Definitions 14 and 15 above are inverses of each other up to isomorphism. Before we turn to a proof of that claim, however, we show that the correspondence \(\zeta \) between index structures and transition structures induces a bijection between the sets of indices of evaluation of the respective structures.
Lemma 8
For any index structure \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \), the function \(\nu : W \rightarrow {\mathsf{Ind}}\mathrm{(}\zeta (\mathcal {W}))\) defined by
is a bijection, and for all \(w,w'\in W\):
- (\(\lhd \)):
-
\(w \lhd w'\) iff \([w]_\sim \ll [w']_\sim \) and \(T_{[w]_\approx } = T_{[w']_\approx }\);
- (\(\sim \)):
-
\(w \sim w'\) iff \([w]_\sim = [w']_\sim \);
- (\(\sqsubseteq \)):
-
\(w \sqsubset w'\) [\(w = w'\)] iff \([w]_\sim = [w']_\sim \) and \(T_{[w]_\approx } \subset T_{[w']_\approx }\) [\(T_{[w]_\approx } = T_{[w']_\approx }\)].
Proof
We show that the function \(\nu \) is a bijection. The injectivity of \(\nu \) is a straightforward consequence of Lemma 5 and the following claim: for all \([w]_\approx \), \([w']_\approx \in {W/\!\!\approx }\),
By Definition 12 (vii), \([w]_\approx \ne [w']_\approx \) implies that either \({\mathsf{Dom}}(f_{w,w'}) \ne [w]_\approx \) or \(\mathsf {Im}(f_{w,w'}) \ne [w']_\approx \), so that consequently \(\sigma ([w]_\approx ) \ne \sigma ([w']_\approx )\). The claim in (5.13) then follows immediately by Proposition 2 (ii). In order to see that \(\nu \) is surjective as well, note that for all \([w]_\sim \in {W/\!\!\sim }\) and \([w']_\approx \in {W/\!\!\approx }\),
because, by (5.11), \({\mathsf{H}}(T_{[w']_\approx }) = {\mathsf{hist}}(\mathcal {T} _{[w']_\approx })\). Now consider any \([w]_\sim /T_{[w']_\approx } \in \mathsf {Ind}(\zeta (\mathcal {W}))\). By (5.14) and Lemma 5 it follows that \([w]_\sim \cap [w']_\approx = \{z\}\) for some \(z \in W\), and hence \([w]_\sim /T_{[w']_\approx } = \nu (z)\).
(\(\lhd \)) That \(w \lhd w'\) implies \([w]_\sim \ll [w']_\sim \) and \(T_{[w]_\approx } = T_{[w']_\approx }\) is straightforward by Definition 15. Conversely, by (5.13), \(T_{[w]_\approx } = T_{[w']_\approx }\) implies \([w]_\approx = [w']_\approx \), and whenever \([w]_\sim \ll [w']_\sim \) holds as well, then, by Lemmas 5 and 7 (i), \(w\lhd w'\).
(\(\sim \)) Straightforward.
(\(\sqsubseteq \)) By Definition 12 (v) and (5.5), \(w \sqsubset w'\) implies \([w]_\sim = [w']_\sim \) and \([w]_\approx \Subset [w']_\approx \). Then, by (5.8), \(\langle \sigma ([w']_\approx ), \ll \rangle \) is a proper pruning of \(\langle \sigma ([w]_\approx ), \ll \rangle \), and hence, by Proposition 2 (iii), \(T_{[w]_\approx } \subset T_{[w']_\approx }\).
Now assume \([w]_\sim = [w']_\sim \) and \(T_{[w]_\approx } \subset T_{[w']_\approx }\). By Proposition 2 (iii), the latter implies that \(\sigma ([w']_\approx ) \subset \sigma ([w]_\approx )\), from which it follows that \({\mathsf{Dom}}(f_{w',w}) = [w']_\approx \). Consequently, by Definition 12 (vii) and Lemmas 5 and 7 (ii), \(w \sqsubset w'\).
Obviously, \(w = w'\) implies \([w]_\sim = [w']_\sim \) and \(T_{[w]_\approx } = T_{[w']_\approx }\). The converse implication is an immediate consequence from (5.13) and Lemma 5. \(\square \)
Theorem 3
For every transition structure \(\mathcal {M}^{\textit{ts}}\) and every index structure \(\mathcal {W} \), (a) \(\zeta (\lambda (\mathcal {M}^{\textit{ts}}))\) is isomorphic to \(\mathcal {M}^{\textit{ts}}\), and (b) \(\lambda (\zeta (\mathcal {W}))\) is isomorphic to \(\mathcal {W} \).
Proof
(a) Let \(\mathcal {M}^{\textit{ts}}= \langle M,<,{\textit{ts}}\rangle \) be any transition structure. Then \(\zeta (\lambda (\mathcal {M}^{\textit{ts}})) = \langle {{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\sim },\ll ,\mathsf {ts}({{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\approx })\rangle \). By Definitions 14 and 15, the function defined by
is a bijection between \({{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\sim }\) and M that is order-preserving: for all \([m/T]_\sim \), \([m'/T']_\sim \in {{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\sim }\), \([m/T]_\sim \ll [m'/T']_\sim \) implies \(m<m'\). Moreover, by (5.1), the mapping \([m/T]_\approx \mapsto T\) is a bijection between \({{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\approx }\) and \({\textit{ts}}\). Then, by Definition 15 and (5.13), the function \(\tau \) defined by
is a bijection between \(\mathsf {ts}({{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\approx })\) and \({\textit{ts}}\), which preserves the inclusion relation: by successive application of Proposition 2 (iii) and Definitions 12 (vii) and 14, it is readily verified that \(\xi (\langle \sigma ([m/T]_\approx ),\ll \rangle ) \subseteq \xi (\langle \sigma ([m'/T']_\approx ),\ll \rangle )\) implies \(T\subseteq T'\). To conclude the first part of the proof, we show that for every \(T\in {\textit{ts}}\), the following holds: every history in \({\mathsf{H}}(\tau (\xi (\langle \sigma ([m/T]_\approx ),\ll \rangle )))\) is the \(\pi \)-image of exactly one history in \({\mathsf{H}}(\xi (\langle \sigma ([m/T]_\approx ),\ll \rangle ))\). Recall that, by (5.11), \({\mathsf{H}}(\xi (\langle \sigma ([m/T]_\approx ),\ll \rangle )) = {\mathsf{hist}}(\langle \sigma ([m/T]_\approx ),\ll \rangle )\), where \(\langle \sigma ([m/T]_\approx ),\ll \rangle \) is order isomorphic to \(\langle [m/T]_\approx ,\lhd \rangle \), which is in turn order isomorphic to \(\langle \bigcup {\mathsf{H}}(T),<\rangle \) (via \(\theta \)), and, by Proposition 1 (i), \({\mathsf{hist}}(\langle \bigcup {\mathsf{H}}(T),<\rangle ) = {\mathsf{H}}(T)\). Then the function \(\pi = \theta \circ \sigma ^{-1}\) induces a bijection between \({\mathsf{H}}(\xi (\langle \sigma ([m/T]_\approx ),\ll \rangle ))\) and \({\mathsf{H}}(\tau (\xi (\langle \sigma ([m/T]_\approx ),\ll \rangle )))\).
(b) Let \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) be any index structure. Then \(\lambda (\zeta (\mathcal {W}))\) equals \(\langle \mathsf {Ind}(\zeta (\mathcal {W})),\lhd \sim ,\sqsubseteq \rangle \), and by Definition 14 and Lemma 8, the function \(\nu : W \rightarrow \mathsf {Ind}(\zeta (\mathcal {W}))\) with \(\nu (w)=[w]_\sim /T_{[w]_\approx }\) is a bijection that preserves the relations \(\lhd \), \(\sim \) and \(\sqsubseteq \). \(\square \)
By Theorem 3, every transition structure is isomorphic to the \(\zeta \)-image of some index structure. On the basis of Lemma 8, the correspondence \(\zeta \) between index structures and transition structures can be extended in a natural way to a correspondence between models. For every index model \(\langle \mathcal {W},v_{{\mathsf{i}}}\rangle \), let \(\zeta (\langle \mathcal {W},v_{{\mathsf{i}}}\rangle )\) be the transition model \(\langle \zeta (\mathcal {W}),\zeta (v_{{\mathsf{i}}})\rangle \) where
We show that the correspondence \(\zeta \) preserves \(\mathcal {L}_\mathsf{t}\)-validity.
Proposition 4
Let \(\mathfrak {W} = \langle \mathcal {W}, v_{{\mathsf{i}}}\rangle \) be an index model on the index structure \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \). Then for every \(\phi \in \mathcal {L}_\mathsf{t}\) and every \(w \in W\),

Proof
The proof runs by induction on the structure of \(\phi \) and rests on the induction hypothesis that the claim holds for any proper subformula \(\psi \) of \(\phi \). Given the correspondence in (5.17), the base clause is straightforward. We restrict ourselves here to the case for the strong future operator \({\mathsf{F}}\), all other cases being similar and simpler.
“\(\Rightarrow \)”: Assume \(\mathfrak {W},w \vDash _{{\mathsf{i}}}{\mathsf{F}}\psi \). Then, by Definition 13, for all \(h\in {\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle )\) s.t. \(w\in h\), there is some \(w'\in h\) s.t. \(w' \rhd w\) and \(\mathfrak {W},w' \vDash _{{\mathsf{i}}}\psi \). For any such future witness \(w'\), Lemma 8 implies \([w']_\sim \gg [w]_\sim \) and \(T_{[w']_\approx } = T_{[w]_\approx }\), so that the induction hypothesis yields \(\zeta (\mathfrak {W}),[w']_\sim /T_{[w]_\approx } \vDash _\mathsf{t}\psi \). Note that, by (5.7) and (5.11), quantification over \({\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle ) \cap {\mathsf{H}}_w\) is equivalent to quantification over \({\mathsf{H}}(T_{[w]_\approx })\cap {\mathsf{H}}_{[w]_\sim }\): every history in \({\mathsf{H}}(T_{[w]_\approx })\cap {\mathsf{H}}_{[w]_\sim }\) is the \(\sigma \)-image of exactly one history in \({\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle ) \cap {\mathsf{H}}_w\). Then Definition 10 implies .
“\(\Leftarrow \)”: Conversely, assume \(\zeta (\mathfrak {W}),[w]_\sim /T_{[w]_\approx } \vDash _\mathsf{t}{\mathsf{F}}\psi \). Then, by Definition 10, for all \(h \in {\mathsf{H}}(T_{[w]_\approx })\) s.t. \([w]_\sim \in h\), there is some \([v]_\sim \in h\) s.t. \([v]_\sim \gg [w]_\sim \) and \(\zeta (\mathfrak {W}),[v]_\sim /T_{[w]_\approx } \vDash _\mathsf{t}\psi \). For any such future witness \([v]_\sim \), let \(w'\in W\) be the unique element in \([v]_\sim \cap [w]_\approx \), which exists by (5.14) and Lemma 5. Then \([v]_\sim = [w']_\sim \) and \([w]_\approx = [w']_\approx \), so that the induction hypothesis yields \(\mathfrak {W},w' \vDash _{{\mathsf{i}}}\psi \). Moreover, by Lemma 8, \(w'\rhd w\). Consequently, by Definition 13, we have \(\mathfrak {W},w \vDash _{{\mathsf{i}}}{\mathsf{F}}\psi \), taking into account the one-to-one correspondence between histories in \({\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle ) \cap {\mathsf{H}}_w\) and histories in \({\mathsf{H}}(T_{[w]_\approx })\cap {\mathsf{H}}_{[w]_\sim }\) induced by \(\sigma \). \(\square \)
Theorem 4
For every \(\phi \in \mathcal {L}_\mathsf{t}\),
Proof
6 First-Order Definability of Index Structures
In the previous section, we have shown that \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. transition structures coincides with \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. index structures. In this section, we show that index structures are first-order definable in a language \(\mathcal {L}^1\) with symbols for \(\lhd , \sim , \sqsubseteq \), which then naturally leads to axiomatizability results for the transition framework.
In order to facilitate readability, we use \(\lhd , \sim , \sqsubseteq \) also as symbols of \(\mathcal {L}^1\). In addition, we assume that \(\mathcal {L}^1\) comprises a symbol for the relation \(\approx \), as defined in (4.1). It is straightforward to verify that clauses (i)–(vi) of Definition 12 can be given first-order renderings in \(\mathcal {L}^1\). We set
-
(FO.0)
the conjunction of all \(\mathcal {L}^1\)-sentences expressing conditions (i)–(vi).
Now consider clause (vii) of Definition 12. Note that by condition (vi) of Definition 12 it is guaranteed that the intersection \(\sim \cap \ ([w]_\approx \times [w']_\approx )\) is non-empty. We state that \(\sim \cap \ ([w]_\approx \times [w']_\approx )\) is an injective, \(\lhd \)-preserving function:
-
(FO.1)
\(\forall w, w', v, v' (w \approx v \wedge w' \approx v' \rightarrow \)
\([(w \sim w' \wedge w \sim v' \rightarrow w' = v') \wedge \)
\((w \sim w' \wedge v \sim w' \rightarrow w= v) \wedge \)
\((w \sim w' \wedge v \sim v' \rightarrow (w \lhd v \leftrightarrow w' \lhd v'))])\).
To state the relevant properties of the function \(f_{w,w'} = \ \sim \cap \ ([w]_\approx \times [w']_\approx )\), we make use of the following abbreviations:
-
(A1)
\(v \in {\mathsf{Dom}}(f_{w,w'}) \ {\mathop {\equiv }\limits ^{d ef}} \ w \approx v \wedge \exists v' ( v' \approx w' \wedge v \sim v')\);
(v belongs to the domain of \(f_{w,w'}\).)
-
(A2)
\(v' \in \mathsf {Im}(f_{w,w'}) \ {\mathop {\equiv }\limits ^{d ef}} \ w' \approx v' \wedge \exists v ( v \approx w \wedge v \sim v')\);
(\(v'\) belongs to the image of \(f_{w,w'}\).)
-
(A3)
\(\text {hist}([w]_\approx ) \ {\mathop {\equiv }\limits ^{d ef}} \ \forall v,v' (w \approx v \wedge w \approx v' \rightarrow (v \unlhd v' \vee v' \unlhd v))\);
(\(\langle [w]_\approx , \lhd \rangle \) consists of a single history.)
-
(A4)
\(w \perp _u v \ {\mathop {\equiv }\limits ^{d ef}} \ u \lhd w \wedge u \lhd v \wedge \forall z(z \unlhd w \wedge z \unlhd v \rightarrow z \unlhd u)\);Footnote 12
(\(w \rhd u \lhd v\) is a branching triangle.)
-
(A5)
\(v \in \mathsf {Trunk}([w]_\approx ) \ {\mathop {\equiv }\limits ^{d ef}} \forall x (x \approx w \rightarrow (x \unlhd v \vee v \unlhd x ))\).
(v belongs to the trunk of \([w]_\approx \).)
Note that both clauses (vii.a) and (vii.b) of Definition 12 require that the domain and the image of \(f_{w,w'}\) be downward closed:
-
(FO.2)
\(\forall w, w', v, v', z, z' ((v\in {\mathsf{Dom}}(f_{w,w'}) \wedge z\lhd v \rightarrow z\in {\mathsf{Dom}}(f_{w,w'})) \wedge \)
\((v'\in \mathsf {Im}(f_{w,w'}) \wedge z'\lhd v' \rightarrow z'\in \mathsf {Im}(f_{w,w'})))\).
Moreover, in both cases \(f_{w,w'}\) is not onto, i.e., the image of \(f_{w,w'}\) is a proper subset of \([w']_\approx \):
-
(FO.3)
\(\forall w, w'\, \exists v'(w' \approx v' \wedge v' \notin \mathsf {Im}(f_{w,w'}))\).
Clause (vii.a) deals with the case in which \(\sqsupset \cap \ ([w]_\approx \times [w']_\approx )\ne \emptyset \). In that case, \(f_{w,w'} = \ \sqsupset \cap \ ([w]_\approx \times [w']_\approx )\) with \({\mathsf{Dom}}(f_{w,w'}) = [w]_\approx \) and \(\langle \mathsf {Im}(f_{w,w'}),\lhd \rangle \) a proper pruning of \(\langle [w']_\approx ,\lhd \rangle \). The fact that \(f_{w,w'} = \ \sqsupset \cap \ ([w]_\approx \times [w']_\approx )\) can be expressed by
-
(FO.4)
\(\forall w, w' (w \sqsupset w' \rightarrow \forall v, v' (v \approx w \wedge v' \approx w' \wedge v \sim v' \rightarrow v \sqsupset v'))\).
The following formula states that the domain of \(f_{w,w'}\) is given by \([w]_\approx \):
-
(FO.5)
\(\forall w, w', v (w \sqsupset w' \wedge w \approx v \rightarrow v\in {\mathsf{Dom}}(f_{w,w'}))\).
In order to give expression to the idea that \(\langle \mathsf {Im}(f_{w,w'}), \lhd \rangle \) is a pruning of \(\langle [w']_\approx , \lhd \rangle \), we distinguish two cases, viz. the case in which \(\langle [w]_\approx , \lhd \rangle \) consists of just a single history and the case in which \(\langle [w]_\approx , \lhd \rangle \) contains a branching point. That is, clause (FO.6) corresponds to the modification (i’) of condition (i) of Definition 11 and clause (FO.7) to condition (ii) of that definition.
-
(FO.6)
\(\forall w, w' (w \sqsupset w' \wedge \text {hist}([w]_\approx ) \rightarrow \)
\(\lnot \exists u' ( w' \approx u' \wedge \forall v' (v' \in \mathsf {Im}(f_{w,w'}) \rightarrow v' \lhd u')))\);
-
(FO.7)
\(\forall w, v, u, u' (w \perp _u v \wedge u \sqsupset u' \rightarrow \)
\(\forall z' (z' \unlhd u' \vee u' \lhd z' \rightarrow z' \in \mathsf {Im}(f_{u,u'})))\).
Let us now consider clause (vii.b), which deals with the case in which \(\sqsupset \cap \ ([w]_\approx \times [w']_\approx ) = \emptyset \) and \(\sqsupset \cap \ ([w']_\approx \times [w]_\approx ) = \emptyset \) with \([w]_\approx \ne [w']_\approx \). In that case, \(f_{w,w'}\) is not only required to be not onto, but the domain of \(f_{w,w'}\) must also be properly included in \([w]_\approx \). What is more, both \({\mathsf{Dom}}(f_{w,w'})\) and \(\mathsf {Im}(f_{w,w'})\) are required to be \(\lhd \)-downward closed subsets of the trunks of \(\langle [w]_\approx ,\lhd \rangle \) resp. \(\langle [w']_\approx ,\lhd \rangle \) that do not contain a branching point. The fact that \({\mathsf{Dom}}(f_{w,w'})\) is a proper subset of \([w]_\approx \) can easily be expressed by
-
(FO.8)
\(\forall w, w' (w \sim w' \wedge w \not \sqsupset w' \wedge w' \not \sqsupset w \wedge w \ne w' \rightarrow \)
\(\exists x (x \approx w \wedge x \notin {\mathsf{Dom}}(f_{w,w'})))\).
The following formula expresses the idea that both the domain and the image of \(f_{w,w'}\) are subsets of the trunks of the respective \(\lhd \)-trees:
-
(FO.9)
\(\forall w, w' (w \sim w' \wedge w \not \sqsupset w' \wedge w' \not \sqsupset w \wedge w \ne w' \rightarrow \)
\(\forall x,x' ((x \in {\mathsf{Dom}}(f_{w,w'}) \rightarrow x \in \mathsf {Trunk}([w]_\approx )) \wedge \)
\( (x' \in \mathsf {Im}(f_{w,w'}) \rightarrow x' \in \mathsf {Trunk}([w']_\approx ))))\).
Finally, neither \({\mathsf{Dom}}(f_{w,w'})\) nor \(\mathsf {Im}(f_{w,w'})\) may contain a branching point in \(\langle [w]_\approx ,\lhd \rangle \) resp. \(\langle [w']_\approx ,\lhd \rangle \):
-
(FO.10)
\(\forall w, w' (w \sim w' \wedge w \not \sqsupset w' \wedge w' \not \sqsupset w \wedge w \ne w' \rightarrow \)
\(\forall x, x' ((x\in {\mathsf{Dom}}(f_{w,w'}) \rightarrow \lnot \exists x_1, x_2 (w \approx x_1 \wedge w \approx x_2 \wedge x_1 \perp _x x_2)) \wedge \)
\((x'\in \mathsf {Im}(f_{w,w'}) \rightarrow \lnot \exists x_1', x_2' (w' \approx x_1' \wedge w' \approx x_2' \wedge x_1' \perp _{x'} x_2')))\).
Proposition 5
Every model \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) of axioms (FO.0)–(FO.10) is an index structure.
Proof
Straightforward. \(\square \)
In this section, we have proven that index structures are first-order definable. Recall that on index structures, the semantic clauses for the intensional operators of the transition language \(\mathcal {L}_\mathsf{t}\)—with the exception of the one for \({\mathsf{F}}\)—involve only first-order quantification over the set W (cf. Definition 13). Moreover, by Theorem 4, \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. transition structures is equivalent to \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. index structures. As a consequence, validity of \({\mathsf{F}}\)-free \(\mathcal {L}_\mathsf{t}\)-formulas w.r.t. transition structures is axiomatizable.
Theorem 5
The set of \({\mathsf{F}}\)-free \(\mathcal {L}_\mathsf{t}\)-validities w.r.t. transition structures is recursively enumerable and hence, by Craig’s theorem, axiomatizable.
Proof
Follows from Definition 13 by Theorem 4 and Proposition 5. \(\square \)
7 Bundled Structures
In this section, we generalize the results established in Sects. 5 and 6 via a ‘Henkin move’ to so-called bundled structures. Rather than considering plain transition structures, we consider transition structures that are endowed with a primitive set of histories that is such that it covers the entire BT structure. A set of histories that fulfills the given requirement is called a bundle (cf. Burgess 1978, 1980). The corresponding index structures will then have to be bundled structures as well, in a sense to be specified below.
Definition 16
(Bundle) Given a BT structure \(\mathcal {M}=\langle M,<\rangle \), a bundle on\(\mathcal {M}\) is a subset \(B \subseteq {\mathsf{hist}}(\mathcal {M})\) s.t. for every \(m \in M\), \(\mathsf {H}_m\cap B \not =\emptyset \).
The need of generalization is triggered by the strong future operator \({\mathsf{F}}\), which involves second-order quantification over histories. In bundled structures, quantification over histories dissolves into first-order quantification over the elements of the bundle. We show that \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. bundled transition structures is equivalent to \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. bundled index structures and that bundled index structures are first-order definable. Hence, \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. bundled transition structures turns out to be axiomatizable.
When it comes to the definition of bundled transition structures, some care is needed in order to avoid conflicts between the primitive set of histories and the primitive set of transition sets.
Definition 17
(Bundled transition structure) A bundled transition structure is a quadruple \(\mathcal {M}^{\textit{ts}}_B = \langle M,<,{\textit{ts}},B\rangle \) where \(\mathcal {M}^{\textit{ts}}= \langle M,<,{\textit{ts}}\rangle \) is a transition structure and B is a bundle on \(\langle M,<\rangle \) s.t. (i) for every \(h\in B\), there is some \(T\in {\textit{ts}}\) s.t. \(h\in {\mathsf{H}}(T)\) and (ii) for every \(T\in {\textit{ts}}\), \({\mathsf{H}}(T)\cap B \not = \emptyset \).
The above definition guarantees that every history of the bundle B is compatible with at least one transition set in \({\textit{ts}}\). Moreover, the definition rules out the possibility that the bundle delimits the set of histories allowed by the transition parameter to the empty set. In a bundled transition structure \(\mathcal {M}^{\textit{ts}}_B = \langle M,<,{\textit{ts}},B\rangle \), for all \(T\in {\textit{ts}}\) and \(m\in M\),
Note that \({\mathsf{H}}(T)\cap \mathsf {H}_m\ne \emptyset \) implies \(\mathsf {H}_m\subseteq {\mathsf{H}}(T)\) or \({\mathsf{H}}(T)\subsetneq \mathsf {H}_m\). If \(\mathsf {H}_m\subseteq {\mathsf{H}}(T)\), the conclusion in (7.1) follows from the fact that B is a bundle on \(\mathcal {M}\), i.e. \(\mathsf {H}_m\cap B \ne \emptyset \). If \({\mathsf{H}}(T)\subsetneq \mathsf {H}_m\), the claim follows from the requirement \({\mathsf{H}}(T)\cap B \ne \emptyset \) in Definition 17 (ii).
When moving from plain transition structures to bundled ones, the set of indices of evaluation remains unaltered. That is to say, every valuation \(v_\mathsf {t}\) on \(\mathcal {M}^{\textit{ts}}\) is also a valuation on \(\mathcal {M}^{\textit{ts}}_B\), and vice versa. The additional set of histories B affects only the clause for the strong future operator \({\mathsf{F}}\); all other semantic clauses stay in place. In bundled transition structures, the semantics of the \({\mathsf{F}}\)-operator is given by the following clause:
- \(({\mathsf{F}})\) :
-
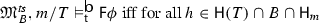 , there is some \(m' \in h\) s.t. \(m' > m\) and
, there is some \(m' \in h\) s.t. \(m' > m\) and 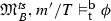 .
.
As said, once transition structures are endowed with a primitive set of histories, the corresponding index structures need to be bundled structures as well. A bundled index structure is an index structure \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) with a primitive set of histories \(\mathbb {B}\) that defines a bundle on every BT structure \(\langle [w]_\approx ,\lhd \rangle \) (for \(w\in W\)). Moreover, whenever \(\langle [w]_\approx ,\lhd \rangle \) is order isomorphic to a pruning of \(\langle [w']_\approx ,\lhd \rangle \), the order isomorphism induces an embedding from the bundle on \(\langle [w]_\approx ,\lhd \rangle \) into the bundle on \(\langle [w']_\approx ,\lhd \rangle \) such that any history in the \(\langle [w']_\approx ,\lhd \rangle \)-bundle that lacks a pre-image in the \(\langle [w]_\approx ,\lhd \rangle \)-bundle does not have a correspondent in \(\langle [w]_\approx ,\lhd \rangle \) at all.
Definition 18
(Bundled index structure) A bundled index structure is a quintuple \(\mathcal {W} _\mathbb {B}= \langle W,\lhd ,\sim ,\sqsubseteq ,\mathbb {B}\rangle \) where \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) is an index structure and \(\mathbb {B}\) is a subset of \(\bigcup _{w \in W} {\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle )\) s.t. for all \(w,w'\in W\),
-
(B1)
\(\mathbb {B}_{[w]_\approx } := {\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle ) \cap \mathbb {B}\) is a bundle on \(\langle [w]_\approx , \lhd \rangle \);
-
(B2)
if \(w \sqsupset w'\), then \(f_{w,w'}({\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle )) \cap \mathbb {B}_{[w']_\approx } = f_{w,w'}(\mathbb {B}_{[w]_\approx })\).
In bundled index structures, the semantic clause for the strong future operator \({\mathsf{F}}\) reads as follows:
- \(({\mathsf{F}})\) :
-
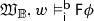 iff for all \(h \in \mathbb {B}_{[w]_\approx }\) s.t. \(w\in h\), there is some \(w' \in h\) s.t. \(w' \rhd w\) and
iff for all \(h \in \mathbb {B}_{[w]_\approx }\) s.t. \(w\in h\), there is some \(w' \in h\) s.t. \(w' \rhd w\) and 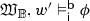 .
.
We show that the correspondence between transition structures and index structures established in Sect. 5 can be extended to bundled structures. To this end, we define extensions of the functions \(\lambda \) and \(\zeta \) introduced in Definitions 14 and 15 above and show that those extensions are again inverses of each other up to isomorphism.
Definition 19
For any bundled transition structure \(\mathcal {M}^{\textit{ts}}_B = \langle M,<,{\textit{ts}},B\rangle \), let \(\lambda (\mathcal {M}^{\textit{ts}}_B)\) be the structure \(\langle \lambda (\mathcal {M}^{\textit{ts}}),\lambda (B)\rangle \) with \(\lambda (\mathcal {M}^{\textit{ts}})\) as defined in Definition 14 and
where \(\theta _T\) is the restriction \(\theta \vert _{[m/T]_\approx }\) of the function \(\theta \) defined in (5.2) for some \(m \in \bigcup {\mathsf{H}}(T)\).
Note that, by (5.1), for all \(m/T, m'/T' \in {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\), \([m/T]_\approx = [m'/T']_\approx \) implies \(\theta _T = \theta _{T'}\).
Proposition 6
For every bundled transition structure \(\mathcal {M}^{\textit{ts}}_B\), the structure \(\lambda (\mathcal {M}^{\textit{ts}}_B)\) is a bundled index structure.
Proof
Recall that, by (5.3), for every \([m/T]_\approx \in {{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\approx }\), \(\theta _T\) is an order isomorphism from \(\langle [m/T]_\approx ,\lhd \rangle \) onto the pruning \(\langle \bigcup {\mathsf{H}}(T),<\rangle \) of \(\langle M,<\rangle \), and, by Proposition 1 (i), \({\mathsf{hist}}(\langle \bigcup {\mathsf{H}}(T),<\rangle ) = {\mathsf{H}}(T)\). Then \(\theta _T^{-1}\) induces a bijection between \({\mathsf{H}}(T)\) and \({\mathsf{hist}}(\langle [m/T]_\approx ,\lhd \rangle )\). We show that \(\lambda (\mathcal {M}^{\textit{ts}}_B)\) fulfills conditions (B1) and (B2) of Definition 18.
Let \(m/T \in {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\). Then \({\mathsf{H}}(T)\cap \mathsf {H}_m\ne \emptyset \). This implies by (7.1) that \({\mathsf{H}}(T)\cap B \cap \mathsf {H}_m\ne \emptyset \). We can then consider some \(h\in {\mathsf{H}}(T)\cap B \cap \mathsf {H}_m\ne \emptyset \). It follows that \(\theta _T^{-1}(h) \in \lambda (B)\) is a history in \(\langle [m/T]_\approx ,\lhd \rangle \) that contains m / T. Consequently, \(\lambda (B)_{[m/T]_\approx }\) is a bundle on \(\langle [m/T]_\approx ,\lhd \rangle \), and hence \(\lambda (\mathcal {M}^{\textit{ts}}_B)\) satisfies condition (B1).
Now assume that there are \(m/T, m'/T' \in {\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})\) s.t. \(m/T \sqsupset m'/T'\). Then by Definition 12 (vii.a) and Lemma 2 it follows that \(f_{m/T,m'/T'}({\mathsf{hist}}(\langle [m/T]_\approx ,\lhd \rangle )) \subsetneq {\mathsf{hist}}(\langle [m'/T']_\approx ,\lhd \rangle )\), and hence \(f_{m/T,m'/T'}(\lambda (B)_{[m/T]_\approx }) \subsetneq \lambda (B)_{[m'/T']_\approx }\). The inclusion \(f_{m/T,m'/T'}(\lambda (B)_{[m/T]_\approx }) \subseteq f_{m/T,m'/T'}({\mathsf{hist}}(\langle [m/T]_\approx ,\lhd \rangle ))\) is trivially fulfilled, and so \(f_{m/T,m'/T'}(\lambda (B)_{[m/T]_\approx }) \subseteq (f_{m/T,m'/T'}({\mathsf{hist}}(\langle [m/T]_\approx ,\lhd \rangle )) \cap \lambda (B)_{[m'/T']_\approx })\).
We show that the converse inclusion holds as well. Assume \(b\in f_{m/T,m'/T'}({\mathsf{hist}}(\langle [m/T]_\approx ,\lhd \rangle )) \cap \lambda (B)_{[m'/T']_\approx }\). Then \(\theta _{T'}(b) \in {\mathsf{H}}(T)\cap \mathsf {H}(T')\cap B\). From this it follows that \(\theta _T^{-1}\circ \theta _{T'}(b) \in \lambda (B)\) is a history in \(\langle [m/T]_\approx ,\lhd \rangle \) and thus its \(f_{m/T,m'/T'}\)-image is a history in \(\lambda (B)_{[m'/T']_\approx }\). This concludes the proof that condition (B2) is satisfied by \(\lambda (\mathcal {M}^{\textit{ts}}_B)\). \(\square \)
Definition 20
For any bundled index structure \(\mathcal {W} _\mathbb {B}= \langle W,\lhd ,\sim ,\sqsubseteq ,\mathbb {B}\rangle \), let \(\zeta (\mathcal {W} _\mathbb {B})\) be the structure \(\langle \zeta (\mathcal {W}),\zeta (\mathbb {B})\rangle \) with \(\zeta (\mathcal {W})\) as defined in Definition 15 and
where \(\sigma \) is the function defined in (5.4).
Proposition 7
For every bundled index structure \(\mathcal {W} _\mathbb {B}\), the structure \(\zeta (\mathcal {W} _\mathbb {B})\) is a bundled transition structure.
Proof
Recall that, by (5.7), for every \([w]_\approx \in {W/\!\!\approx }\), \(\sigma \vert _{[w]_\approx }\) is an order isomorphism from \(\langle [w]_\approx ,\lhd \rangle \) onto a pruning of \(\langle {W/\!\!\sim },\ll \rangle \). Then \(\sigma \) maps histories in \(\langle [w]_\approx ,\lhd \rangle \) to histories in \(\langle {W/\!\!\sim },\ll \rangle \). Moreover, by (5.11), \({\mathsf{hist}}(\sigma (\langle [w]_\approx ,\lhd \rangle )) = {\mathsf{H}}(\xi (\sigma (\langle [w]_\approx ,\lhd \rangle )))\). We show that \(\zeta (\mathcal {W} _\mathbb {B})\) fulfills Definition 17.
We first prove that \(\zeta (\mathbb {B})\) is a bundle on \(\langle {W/\!\!\sim },\ll \rangle \). Let \([w]_\sim \in {W/\!\!\sim }\). Since \(\mathbb {B}_{[w]_\approx }\) is a bundle on \(\langle [w]_\approx ,\lhd \rangle \), there is some \(b\in \mathbb {B}_{[w]_\approx }\) s.t. \(w\in b\). Then \(\sigma (b) \in \zeta (\mathbb {B})\) is a history in \(\langle {W/\!\!\sim },\ll \rangle \) that contains \([w]_\sim \).
We now verify the compatibility of \(\mathsf {ts}({W/\!\!\approx })\) and \(\zeta (\mathbb {B})\). First, let \(h\in \zeta (\mathbb {B})\). Then there is some \(b \in \mathbb {B}\) s.t. \(h = \sigma (b)\). Consequently, there is some \(w\in W\) s.t. \(b\in {\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle )\), and hence h is a history in \({\mathsf{H}}(\xi (\sigma (\langle [w]_\approx ,\lhd \rangle )))\).
Finally, let \(\xi (\sigma (\langle [w]_\approx ,\lhd \rangle )) \in \mathsf {ts}({W/\!\!\approx })\). Then for all \(b \in \mathbb {B}_{[w]_\approx }\), \(\sigma (b)\in \zeta (\mathbb {B})\) is a history in \({\mathsf{H}}(\xi (\sigma (\langle [w]_\approx ,\lhd \rangle )))\). \(\square \)
Theorem 6
For every bundled transition structure \(\mathcal {M}^{\textit{ts}}_B\) and every bundled index structure \(\mathcal {W} _\mathbb {B}\), (a) \(\zeta (\lambda (\mathcal {M}^{\textit{ts}}_B))\) is isomorphic to \(\mathcal {M}^{\textit{ts}}_B\), and (b) \(\lambda (\zeta (\mathcal {W} _\mathbb {B}))\) is isomorphic to \(\mathcal {W} _\mathbb {B}\).
Proof
(a) Let \(\mathcal {M}^{\textit{ts}}_B = \langle M,<,{\textit{ts}},B\rangle \) be any bundled transition structure. Then \(\zeta (\lambda (\mathcal {M}^{\textit{ts}}_B)) = \langle {{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\sim },\ll ,\mathsf {ts}({{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\approx }),B'\rangle \) where
In Theorem 3 (a) we have shown that \(\zeta (\lambda (\mathcal {M}^{\textit{ts}}))\) is isomorphic to \(\mathcal {M}^{\textit{ts}}\). In particular, we have shown that \(\pi : [m/T]_\sim \mapsto m\) is an order isomorphism from \({{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\sim }\) onto M and \(\tau : \xi (\sigma (\langle [m/T]_\approx ,\lhd \rangle )) \mapsto T\) is an order isomorphism from \(\mathsf {ts}({{\mathsf {Ind}}(\mathcal {M}^{\textit{ts}})/\!\!\approx })\) onto \({\textit{ts}}\) s.t. \(\pi = \theta \circ \sigma ^{-1}\) is a bijection between \({\mathsf{H}}(\xi (\langle \sigma ([m/T]_\approx ),\ll \rangle ))\) and \({\mathsf{H}}(T)\). Since for every \(h\in B\), there is some \(T\in {\textit{ts}}\) s.t. \(h\in {\mathsf{H}}(T)\), \(\pi \) induces a bijection between \(B'\) and B s.t. for all \(T\in {\textit{ts}}\) the following holds: every history in \({\mathsf{H}}(T)\cap B\) is the \(\pi \)-image of exactly one history in \({\mathsf{H}}(\xi (\langle \sigma ([m/T]_\approx ),\ll \rangle )) \cap B'\).
(b) Let \(\mathcal {W} _\mathbb {B}= \langle W,\lhd ,\sim ,\sqsubseteq ,\mathbb {B}\rangle \) be any bundled index structure. Then \(\lambda (\zeta (\mathcal {W} _\mathbb {B})) = \langle \mathsf {Ind}(\zeta (\mathcal {W})),\lhd \sim ,\sqsubseteq ,\mathbb {B}'\rangle \) where
In Theorem 3 (b) we have shown that \(\lambda (\zeta (\mathcal {W}))\) is isomorphic to \(\mathcal {W} \). In particular, we have shown that \(\nu : w \mapsto [w]_\sim /T_{[w]_\approx }\) is a bijection between W and \(\mathsf {Ind}(\zeta (W))\) that preserves the relations \(\lhd \), \(\sim \) and \(\sqsubseteq \). Note that for all \(w\in W\), \(\nu (w) = \theta _{T_{[w]_\approx }}^{-1} \circ \sigma (w)\). We show that \(\nu ^{-1}\) induces a bijection between \(\mathbb {B}'\) and \(\mathbb {B}\). In particular, we show that for every \(w\in W\), \(\nu ^{-1}\) induces a bijection between \(\mathbb {B}'_{[\nu (w)]_\approx }\) and \(\mathbb {B}_{[w]_\approx }\). To this end, we prove that every \(\theta ^{-1}_{T_{[w]_\approx }}(h) \in \mathbb {B}'\) has an element \(b\in \mathbb {B}_{[w]_\approx }\) as its \(\nu ^{-1}\)-image. Let \(\theta ^{-1}_{T_{[w]_\approx }}(h) \in \mathbb {B}'\). Then \(h\in {\mathsf{H}}(T_{[w]_\approx }) = {\mathsf{hist}}( \mathcal {T} _{[w]_\approx })\) and hence h is the \(\sigma \)-image of some history \(b \in {\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle )\). Assume for reductio that \(b\notin \mathbb {B}_{[w]_\approx }\). Then there must be some \(w'\in W\) and some \(b'\in \mathbb {B}_{[w']_\approx }\) s.t. \(h=\sigma (b') = \sigma (b)\). By Definition 12 (vii) this implies that \(\langle [w]_\approx ,\lhd \rangle \) and \(\langle [w']_\approx ,\lhd \rangle \) must be pruning related via the \(\lhd \)-isomorphism induced by \(\sim \). However, by condition (B2) of Definition 18, \(\langle [w']_\approx ,\lhd \rangle \) cannot be isomorphic to a pruning of \(\langle [w]_\approx ,\lhd \rangle \) because \(b'\in \mathbb {B}_{[w']_\approx }\) and \(b\notin \mathbb {B}_{[w]_\approx }\). Likewise, by the very same condition, \(\langle [w]_\approx ,\lhd \rangle \) cannot be isomorphic to a pruning of \(\langle [w']_\approx ,\lhd \rangle \) as \(b\in {\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle )\setminus \mathbb {B}\) and \(b'\in \mathbb {B}_{[w']_\approx }\). Consequently, since every history in \(\mathbb {B}\) is a history in some \(\langle [w]_\approx ,\lhd \rangle \) (for \(w\in W\)), \(\nu ^{-1}\) induces a bijection between \(\mathbb {B}'\) and \(\mathbb {B}\). \(\square \)
Since moving to bundled structures does not affect the set of indices of evaluation, on the basis of Theorem 6, the correspondence \(\zeta \) between index models and transition models provided in (5.17) straightforwardly extends to bundled structures. We show that the extension preserves \(\mathcal {L}_\mathsf{t}\)-validity.
Proposition 8
Let \(\mathfrak {W}_\mathbb {B}= \langle \mathcal {W} _\mathbb {B},v_{{\mathsf{i}}}\rangle \) be an index model on the bundled index structure \(\mathcal {W} _\mathbb {B}= \langle W,\lhd ,\sim ,\sqsubseteq ,\mathbb {B}\rangle \). Then for every \(\phi \in \mathcal {L}_\mathsf{t}\) and every \(w\in W\),

Proof
The proof is analogous to that of Proposition 4 and runs by induction on the structure of \(\phi \). In the case of the strong future operator \({\mathsf{F}}\), the proof makes use of the fact that, on the basis of (5.7), (5.11) and Definition 20, \(\sigma \) induces a bijection between histories in \({\mathsf{hist}}(\langle [w]_\approx ,\lhd \rangle ) \cap \mathbb {B}\cap {\mathsf{H}}_w\) and histories in \({\mathsf{H}}(T_{[w]_\approx }) \cap \zeta (\mathbb {B}) \cap {\mathsf{H}}_{[w]_\sim }\). \(\square \)
Theorem 7
For every \(\phi \in \mathcal {L}_\mathsf{t}\),
Proof
Follows from Theorem 6 and Proposition 8. \(\square \)
We now show that bundled index structures \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq ,\mathbb {B}\rangle \) are first-order definable in a two-sorted language \(\mathcal {L}^1_\mathcal {B}\), which extends \(\mathcal {L}^1\) by new variables that are to be interpreted by the elements of the bundle \(\mathbb {B}\) and a new relation symbol \(\varepsilon \) that is meant to represent membership. Thus, in \(\mathcal {L}^1_\mathcal {B}\), we have W-variables and \(\mathbb {B}\)-variables. For w a W-variable and b a \(\mathbb {B}\)-variable, \(w{\, \varepsilon \,}b\) is a well-formed formula of \(\mathcal {L}^1_\mathcal {B}\).
We make use of the following abbreviations:
-
(A6)
\(b \in \mathbb {B}_{[w]_\approx } \ {\mathop {\equiv }\limits ^{d ef}} \ \exists w' (w' \approx w \wedge w' {\, \varepsilon \,}b)\);
(b represents a history in \(\mathbb {B}_{[w]_\approx }\).)
-
(A7)
\(\begin{array}{ll} b' = f_{w,w'}(b) \ {\mathop {\equiv }\limits ^{d ef}} \ &{} b \in \mathbb {B}_{[w]_\approx } \wedge b' \in \mathbb {B}_{[w']_\approx } \wedge \\ &{} \forall v (v {\, \varepsilon \,}b \rightarrow \exists v'(v' {\, \varepsilon \,}b' \wedge v \sqsupset v')) \wedge \\ &{} \forall v' (v' {\, \varepsilon \,}b' \rightarrow \exists v(v {\, \varepsilon \,}b \wedge v \sqsupset v')). \end{array}\)
(\(b'\) represents the \(f_{w,w'}\)-image of the history represented by b.)
Note that the abbreviation (A7) presupposes that \(f_{w,w'} = \ \sqsupset \ \cap \ ([w]_\approx \times [w']_\approx )\).
The properties of the set \(\mathbb {B}\) in a bundled index structure \(\langle W,\lhd ,\sim ,\sqsubseteq ,\mathbb {B}\rangle \) can then be expressed by the following \(\mathcal {L}^1_\mathcal {B}\) formulas: clause (FO.B.0) gives expression to the idea that every element of \(\mathbb {B}\) represents a history in some \(\langle [w]_\approx , \lhd \rangle \) (for \(w\in W\)), while clauses (FO.B.1) and (FO.B.2) correspond to conditions (B1) and (B2) of Definition 18, respectively:
-
(FO.B.0)
\(\forall b\, \exists w (w {\, \varepsilon \,}b)\ \wedge \)
\(\forall b\, \forall w,w' (w {\, \varepsilon \,}b \wedge w' {\, \varepsilon \,}b \rightarrow (w \unlhd w' \vee w' \unlhd w ))\ \wedge \)
\(\forall b\, \forall w,w'(w {\, \varepsilon \,}b \wedge w' \lhd w \rightarrow w' {\, \varepsilon \,}b)\ \wedge \)
\(\forall b\, \lnot \exists w' \,\forall w(w {\, \varepsilon \,}b \rightarrow w \lhd w')\);
-
(FO.B.1)
\(\forall w \exists b (w {\, \varepsilon \,}b)\);
-
(FO.B.2)
\(\forall w, w' (w \sqsupset w' \rightarrow \)
\([\forall b'(b' \in \mathbb {B}_{[w']_\approx } \wedge \forall v'(v'{\, \varepsilon \,}b' \rightarrow v' \in \mathsf {Im}(f_{w,w'})) \rightarrow \)
\(\exists b(b \in \mathbb {B}_{[w]_\approx } \wedge b' = f_{w,w'}(b))) \wedge \)
\(\forall b(b \in \mathbb {B}_{[w]_\approx } \rightarrow \exists b' (b' \in \mathbb {B}_{[w']_\approx } \wedge b' = f_{w,w'}(b)))])\).
Every \(\mathcal {L}^1\)-interpretation \(\mathcal {W} = \langle W,\lhd ,\sim ,\sqsubseteq \rangle \) can naturally be extended to an \(\mathcal {L}^1_\mathcal {B}\)-interpretation \(\mathcal {W} _\mathcal {B}= \langle W,\mathcal {B},\lhd ,\sim ,\sqsubseteq ,{\, \varepsilon \,}\rangle \) by considering a new set \(\mathcal {B}\) and a relation \({\, \varepsilon \,}\subseteq W \times \mathcal {B}\). In such an \(\mathcal {L}^1_\mathcal {B}\)-interpretation, the elements \(b\in \mathcal {B}\) are first of all arbitrary objects, but we want them to represent histories in some \(\langle [w]_\approx ,\lhd \rangle \) (for \(w\in W\)). The obvious candidate for the history represented by an element \(b \in \mathcal {B}\) is \(h_b = \{w \in W \mid w {\, \varepsilon \,}b\}\).Footnote 13
Proposition 9
Let \(\mathcal {W} _\mathcal {B}= \langle W, \mathcal {B}, \lhd ,\sim ,\sqsubseteq , {\, \varepsilon \,}\rangle \) be a model of axioms (FO.0)–(FO.10) and (FO.B.0)–(FO.B.2), and let \(\mathbb {B}\) be \(\{h_b \mid b \in \mathcal {B}\}\). Then \(\mathcal {W} _\mathbb {B}= \langle W,\lhd ,\sim ,\sqsubseteq ,\mathbb {B}\rangle \) is a bundled index structure.
Proof
Straightforward. \(\square \)
As said, the need of generalization to bundled structures was triggered by the strong future operator \({\mathsf{F}}\), whose index semantics involves second-order quantification over histories. By Proposition 9, in bundled index structures, the truth conditions for \({\mathsf{F}}\) can now be expressed as follows:

We then have the following theorem:
Theorem 8
The set of \(\mathcal {L}_\mathsf{t}\)-validities w.r.t. bundled transition structures is recursively enumerable and hence, by Craig’s theorem, axiomatizable.
Proof
Follows from Definition 13 and (7.2) by Theorem 7 and Proposition 9. \(\square \)
8 Concluding Remarks
In this paper, we have shown that \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. (bundled) transition structures is equivalent to \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. (bundled) index structures, which are first-order definable Kripke structures. As a consequence,
-
\({\mathsf{F}}\)-free \(\mathcal {L}_\mathsf{t}\)-validity w.r.t. transition structures is axiomatizable;
-
\(\mathcal {L}_\mathsf{t}\)-validity w.r.t. bundled transition structures is axiomatizable.
With those results in place, the obvious next step for future work is to provide an explicit list of axioms and derivation rules that is complete for validity w.r.t. (bundled) index structures. A chronicle construction on index structures that proceeds by the elimination of counterexamples is expected to prove successful to this end.
Another important issue concerns the question whether validity w.r.t. bundled transition structures is properly weaker than validity w.r.t. plain transition structures. The ‘Henkin move’ to bundled structures was triggered by the need to avoid the Peircean-like second-order quantification over histories in the index semantics for the strong future operator \({\mathsf{F}}\). In Burgess (1980) it is shown that in the Peircean case, bundled tree validity coincides with validity w.r.t. plain BT structures. Even though BT structures are much less complex than index structures, investigating the possibility of transferring Burgess’ result to our case seems worthwhile.
Notes
The requirement of jointedness is non-standard. Standardly, it is only required that any two moments in M have a common lower <-bound in M. The stronger requirement is imposed here because it allows for a perspicuous definition of transitions (cf. Definition 4).
As will become apparent, two transition sets that allow exactly the same histories are equivalent from a logical point of view, i.e. they represent the same possible course of events.
By endowing BT structures with a primitive set of transition sets \({\textit{ts}}\subseteq {\mathsf{dcts}}(\mathcal {M})\), we obtain a variation of the semantics in which unrestricted higher-order quantification over transition sets is replaced by restricted first-order quantification over the set \({\textit{ts}}\). The idea goes back to Henkin (1950). The technique is prominent in branching time logics, where it forms the basis of the notion of a bundled tree (cf. Burgess 1978, 1980). In bundled trees, unrestricted second-order quantification over histories dissolves into restricted first-order quantification over a primitive set of histories, the so-called bundle. We will come back to the notion of a bundled tree in Sect. 7 below.
For a detailed discussion of the notion of a pruning, the correspondence between transition sets and prunings as well as the resulting definition of an index structure, see also Rumberg (2016b, Ch. 3).
Note that the condition \(\mathcal {M}'\in {\mathsf{prun}}(\mathcal {M})\) is not needed in the proof. The statement holds for any \(\mathcal {M}',\mathcal {M}''\) s.t. \(\mathcal {M}'' \in {\mathsf{prun}}(\mathcal {M})\) and \(\mathcal {M}'' \subseteq \mathcal {M}' \subseteq \mathcal {M}\).
Condition (vii.b.i) is needed to cover the limiting case in which \(\langle [w]_\approx ,\lhd \rangle \) or \(\langle [w']_\approx ,\lhd \rangle \) consist of just a single history and hence are identical to their trunks. In case both structures consist of more than a single history, condition (vii.b.i) is implied by condition (vii.b.ii).
If \(\langle [w]_\approx ,\lhd \rangle \) and \(\langle [w']_\approx ,\lhd \rangle \) are \(\sqsubset \)-incomparable and there is some \(w''\in W\) s.t. both the intersections \(\sqsupset \cap \ ([w]_\approx \times [w'']_\approx )\) and \(\sqsupset \cap \ ([w']_\approx \times [w'']_\approx )\) are non-empty, condition (vii.b.iii) follows from condition (vii.a).
Unlike the strong future operator \({\mathsf{F}}\), the operator \({\mathsf{F}}^\sharp \) considered in Rumberg (2016a, Sect. 3.2) is a genuine Kripke-style operator in the index semantics. In the case of the \({\mathsf{F}}^\sharp \)-operator, quantification over histories is replaced by quantification over the possible future extensions of the given transition set. We have \(\mathfrak {W},w \vDash _{{\mathsf{i}}}{\mathsf{F}}^\sharp \phi \) iff for all \(w' \in W\) s.t. \(w' \sqsupseteq w\), there is some \(x' \rhd w'\) s.t. for all \(x \in W\) s.t. \(x' \sqsupseteq x\) and \(x \rhd w\), \(\mathfrak {W},x \vDash _{{\mathsf{i}}}\phi \).
Note that the correspondence between transition structures and index structures incorporates Peirceanism and Ockhamism as limiting cases.
When we apply the function \(\sigma \) to an \(\approx \)-equivalence class, we consider the natural extension of \(\sigma \) to the powerset of W.
Note that \(w \perp _u v\) implies that w and v are not \(\lhd \)-comparable.
References
Burgess, J. P. (1978). The unreal future. Theoria, 44(3), 157–179.
Burgess, J. P. (1979). Logic and time. The Journal of Symbolic Logic, 44(4), 566–582.
Burgess, J. P. (1980). Decidability for branching time. Studia Logica, 39(2/3), 203–218.
Gabbay, D. (1981). An irreflexivity lemma with applications to axiomatizations of conditions on tense frames. In U. Mönnich (Ed.), Aspects of philosophical logic. Synthese library (Vol. 147). Dordrecht: Springer. pp. 67–89.
Gurevich, Y., & Shelah, S. (1985). The decision problem for branching time logic. The Journal of Symbolic Logic, 50(3), 668–681.
Henkin, L. (1950). Completeness in the theory of types. The Journal of Symbolic Logic, 15(2), 81–91.
Prior, A. N. (1967). Past, present and future. Oxford: Oxford University Press.
Reynolds, M. (2002). Axioms for branching time. Journal of Logic and Computation, 12(4), 679–697.
Rumberg, A. (2016a). Transition semantics for branching time. Journal of Logic, Language and Information, 25(1), 77–108.
Rumberg, A. (2016b). Transitions toward a semantics for real possibility. Quaestiones Infinitae: Publications of the Department of Philosophy and Religious Studies (Vol. 98). Ph.D. Thesis, Utrecht University.
Thomason, R. H. (1970). Indeterminist time and truth-value gaps. Theoria, 36(3), 264–281.
van Benthem, J. (1999). Temporal patterns and modal structure. Logic Journal of the IGPL, 7(1), 7–26.
Zanardo, A. (1985). A finite axiomatization of the set of strongly valid Ockhamist formulas. Journal of Philosophical Logic, 14, 447–468.
Zanardo, A. (1990). Axiomatization of ‘Peircean’ branching-time logic. Studia Logica, 49(2), 183–195.
Zanardo, A. (1996). Branching-time logic with quantification over branches: The point of view of modal logic. The Journal of Symbolic Logic, 61(1), 1–39.
Zanardo, A. (2006a). Moment/history duality in Prior’s logics of branching time. Synthese, 150(3), 483–507.
Zanardo, A. (2006b). Quantification over sets of possible worlds in branching-time semantics. Studia Logica, 82(3), 379–400.
Acknowledgements
We would like to thank the reviewers of this journal for valuable and insightful comments on the paper. Antje Rumberg acknowledges support by the Netherlands Organisation for Scientific Research (NWO VIDI 276-20-013) and by the German Research Foundation (DFG FOR 1614 TP7, MU1816/7-1).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rumberg, A., Zanardo, A. First-Order Definability of Transition Structures. J of Log Lang and Inf 28, 459–488 (2019). https://doi.org/10.1007/s10849-018-9276-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-018-9276-4









 iff for all
iff for all 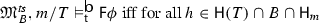 , there is some
, there is some 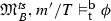 .
.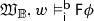 iff for all
iff for all 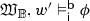 .
.