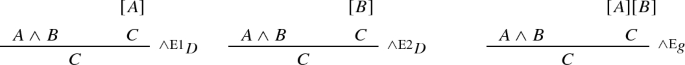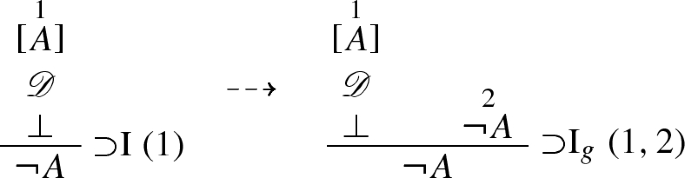Abstract
Developing early results of Prawitz, Tennant proposed a criterion for an expression to count as a paradox in the framework of Gentzen’s natural deduction: paradoxical expressions give rise to non-normalizing derivations. Two distinct kinds of cases, going back to Crabbé and Tennant, show that the criterion overgenerates, that is, there are derivations which are intuitively non-paradoxical but which fail to normalize. Tennant’s proposed solution consists in reformulating natural deduction elimination rules in general (or parallelized) form. Developing intuitions of Ekman we show that the adoption of general rules has the consequence of hiding redundancies within derivations. Once reductions to get rid of the hidden redundancies are devised, it is clear that the adoption of general elimination rules offers no remedy to the overgeneration of the Prawitz–Tennant analysis. In this way, we indirectly provide further support for a solution to one of the two overgeneration cases developed in previous work.
Similar content being viewed by others
Notes
In rule schemata we indicate in square brackets the assumptions which can be discharged by rule applications. In actual derivations we indicate discharge with numbers placed above the discharged assumptions and repeated next to the rule label. In schematic derivations we use square brackets to indicate an arbitrary number of occurrences of a formula, if the formulas is in assumption position, or of the whole sub-derivation having the formula in brackets as conclusion.
Instead of looping reduction sequences one can, more generally, consider non-terminating reduction sequences, which covers paradoxes such as Yablo’s (see Tennant 1995). In the following, we will throughout speak of the looping feature of paradoxical derivations, keeping in mind that “non-termination” of reduction sequences is the appropriate more general term.
We observe that there is a fundamental distinction between Ekman and, say, \(\supset \)-Red in that the latter is a means of getting rid of an application of an introduction rule followed by an application of the corresponding elimination and is thus an immediate consequence of the “harmony” governing the two rules. Not so for Ekman, that may thus be seen as lacking a prima facie plausible meaning-theoretical justification. This remark has been fully developed in Schroeder-Heister and Tranchini (2017) to untrigger the kind of overgeneration discussed in this section.
Elia Zardini observes that the derivations \(\mathbf {E}\) and \(\mathbf {E'}\) are paradoxical because there are instances of them which are paradoxical. Observe however, that \(\mathbf {R}\) and \(\mathbf {R'}\) are not simply instances of \(\mathbf {E}\) and \(\mathbf {E'}\), as they do not arise by simply instantiating A with \(\rho \), but moreover by replacing the assumptions \(\lnot A\mathbin {\supset }A\) and \(A\mathbin {\supset }\lnot A\) with genuine inferential steps, and it is to these steps that the source of paradoxicality is—in Tennant’s intentions—to be ascribed.
In the mentioned article, we also discuss and refute an attempted dismissal of the Prawitz–Tennant analysis based on a supposed case of undergeneration due to Rogerson (2007). A general investigation of possibly systematic undergeneration cases is the object of current research by the authors.
It should be observed that von Plato (2000) is not in the least interested in the issue of paradoxes, and regards Ekman’s phenomenon as a problem for normalization in minimal propositional logic.
Similar modifications of the rules of the quantifiers are required as well, see, e.g., Tennant (1978, §7.10).
The following rules are in fact a simplification of Tennant’s rules obtained by omitting some premises and dischargeable assumptions of the form \(\exists !t\). The reason for the simplification is that they help making the presentation and the discussion more concise. Each derivation using these rules should be understood as an abbreviation of a derivation using Tennant’s original rules. The interested reader can easily reconstruct full derivations by adding the (in most cases trivial) sub-derivations of each of the missing premises of each rule application.
The two notions of general rule and decomposing inference do not in general coincide, since according to the schema given by Ekman the decomposing inferences associated with the conjunction elimination rules of Gentzen (1935) and Prawitz (1965) differ from the (more commonly adopted) single elimination rule considered by Schroeder-Heister (1981) following Prawitz (1979):
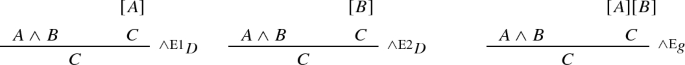
It is finally worth observing that the notion of decomposing inference is not restricted to elimination rules only. When applied to introduction rules, it yields what Negri and von Plato (2001, p. 213ff.) called general introduction rules. More on this in Sect. 5 below.
In fact, general introduction rules are nothing but the decomposing inference corresponding to the usual introduction rules according to the pattern proposed by Ekman given in Sect. 4.1 above.
To obtain a derivation in a system in which all rules are in general form, one should have to add an extra discharged premise in correspondence to the application of \(\supset \)I so to turn it into an application of \(\supset \)I\(_g\) :
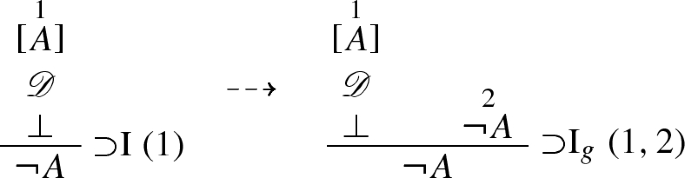
References
Crabbé, M. (n.d.) Non-normalisation de ZF/Counterexample to normalisation for ZF. Sketch of the result presented at the Proof Theory Symposium held in Kiel in 1974. http://www.logic-center.be/Publications/Bibliotheque/contreexemple.pdf.
Ekman, J. (1994). Normal proofs in set theory. Ph.D. thesis, University of Göteborg.
Ekman, J. (1998). Propositions in propositional logic provable only by indirect proofs. Mathematical Logic Quarterly, 44, 69–91.
Gentzen, G. (1935). Untersuchungen über das logische Schließen. Mathematische Zeitschrift, 39, 176–210, 405–431. Engl. transl. ‘Investigations into logical deduction’, in M. E. Szabo (Ed.), The collected papers of Gerhard Gentzen, 1969 (pp. 68–131). North-Holland.
Hallnäs, L. (1988). On normalization of proofs in set theory. Dissertationes Mathematicae, Vol. 261, Institute of Mathematics of the Polish Academy of Sciences, 1988.
Hallnäs, L. (1991). Partial inductive definitions. Theoretical Computer Science, 87, 115–142.
Milne, P. (2014). Inversion principles and introduction rules. In H. Wansing (Ed.), Dag Prawitz on proofs and meaning (pp. 189–224). Berlin: Springer.
Müller, G. H., Oberschelp, A., & Potthoff, K. (Eds.) (1975). ISILC—Logic Conference, Proceedings of the International Summer Institute and Logic Colloquium, Kiel 1974 (Vol. 499). Berlin: Springer.
Negri, S., & von Plato, J. (2001). Structural proof theory. Cambridge: Cambridge University Press.
Prawitz, D. (1965). Natural deduction. A proof-theoretical study. Stockholm: Almqvist & Wiksell. Reprinted in 2006 for Dover Publications.
Prawitz, D. (1979). Proofs and the meaning and completeness of the logical constants. In J. Hintikka, I. Niiniluoto & E. Saarinen (Eds.), Essays on mathematical and philosophical logic: Proceedings of the Fourth Scandinavian Logic Symposium and the First Soviet-Finnish Logic Conference, Jyväskylä,Finland, June 29–July 6, 1976 (pp. 25–40). Dordrecht: Kluwer.
Ripley, D. (2013). Paradoxes and failure of cut. Australasian Journal of Philosophy, 91, 139–164.
Rogerson, S. (2007). Natural deduction and Curry’s paradox. Journal of Philosophical Logic, 36, 155–179.
Schroeder-Heister, P. (1981). Untersuchungen zur regellogischen Deutung von Aussagenverknüpfungen. Ph.D. thesis, University of Bonn.
Schroeder-Heister, P. (2011). Implications-as-rules vs. implications-as-links: An alternative implication-left schema for the sequent calculus. Journal of Philosophical Logic, 40, 95–101.
Schroeder-Heister, P. (2012). Proof-theoretic semantics, self-contradiction, and the format of deductive reasoning. Topoi, 31, 77–85.
Schroeder-Heister, P. (2014). Generalized elimination inferences, higher-level rules, and the implications-as-rules interpretation of the sequent calculus. In L. C. Pereira, E. Haeusler, & V. de Paiva (Eds.), Advances in natural deduction (pp. 1–29). Belin Heidelberg: Springer.
Schroeder-Heister, P., & Tranchini, L. (2017). Ekman’s paradox. Notre Dame Journal of Formal Logic, 58, 567–581.
Sundholm, G. (1979). Review of Michael Dummett: Elements of intuitionism. Theoria, 45, 90–95.
Tennant, N. (1978). Natural logic. Edimburgh: Edimburgh University Press.
Tennant, N. (1982). Proof and paradox. Dialectica, 36, 265–296.
Tennant, N. (1995). On paradox without self-reference. Analysis, 55, 199–207.
Tennant, N. (2002). Ultimate normal form for parallelized natural deduction. Logical Journal of the IGPL, 10, 299–337.
Tennant, N. (2016). Normalizability, cut eliminability and paradox. Synthese. https://doi.org/10.1007/s11229-016-1119-8.
Tranchini, L. (2016). Proof-theoretic semantics, paradoxes, and the distinction between sense and denotation. Journal of Logic and Computation, 26, 495–512.
Tranchini, L. (2018). Proof, meaning and paradox: Some remarks. Topoi. https://doi.org/10.1007/s11245-018-9552-6.
von Plato, J. (2000). A problem of normal form in natural deduction. Mathematical Logic Quarterly, 46, 121–124.
von Plato, J. (2001). Natural deduction with general elimination rules. Archive for Mathematical Logic, 40, 541–567.
Acknowledgements
This work was carried out within the French-German ANR-DFG project “Beyond Logic: Hypothetical Reasoning in Philosophy of Science, Informatics, and Law”, DFG Grant Schr 275/17-1, the DFG Projects “Logical consequence and paradoxical reasoning”, DFG Grant Tra1112/3-1, “Falsity and refutations: Understanding the negative side of logic”, DFG Grant Tra1112/4-1, and the project “Logic and Substructurality” funded by the Ministerio de Economía, Industria y Competitividad, Government of Spain (Grant No. FFI2017-84805-P). We are very grateful to Ole Hjortland, Lucas Rosenblatt and Elia Zardini for many insightful comments on a previous version of this article.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
Schroeder-Heister, P., Tranchini, L. How to Ekman a Crabbé-Tennant. Synthese 199 (Suppl 3), 617–639 (2021). https://doi.org/10.1007/s11229-018-02018-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-018-02018-3